以“高考母题”为驱动 提高数学一轮复习效率
⦿江苏省常熟市海虞中学
石雨茹
1 引言
高三一轮复习的目标是通过有限时间有所侧重地帮助学生回顾所学知识,让整个高中阶段的数学知识系统化、网络化和螺旋式地整合与提升.如何提高一轮复习的质量,让复习效率最大化是每个高三数学教师必须面对,且始终密切关注的问题.为了让一轮复习达到既夯实基础,又提升能力的目的,笔者认为,以课本例题为素材,巧妙改造为高考母题进行针对性地强化训练,可以达到巩固记忆、启迪思维、形成能力和提高素养的多重效能.
2 对“高考母题”的解读
所谓的“高考母题”,可以是教材中的一些典型例习题,也可以是这些例习题的变形,它对应高中数学知识中最基本、最典型、最关键的知识点,是培养创新能力和问题解决能力的源泉.以“高考母题”为载体进行训练,可以帮助学生快速厘清概念、把握原理、掌握规律,实现知识向能力的飞跃,让知识与能力呈现螺旋上升的趋势.
3 以“高考母题”为驱动提高复习效率的策略
3.1 善用“高考母题”,一题多解
善用“高考母题”进行一题多解的训练,可以让学生从多角度、多方位、多层次的分析和尝试中厘清问题本质,活化思维,以达到触类旁通之效.在这个过程中,教师应关注讲解的开放性和发散性,鼓励学生解法的多样化,这样才能以题带知识点和解题技巧,这才是复习课的最佳效果.
例1已知圆C:x2+y2=r2,证明:过圆C上的一点M(x0,y0)的切线方程为x0x+y0y=r2.
抛出问题后,笔者放手让学生去自主探究、合作讨论,激励学生大胆联想和猜想.正是由于有了足够的思考和探究时空,学生生成了多种证明方法,才有了如下登台展示的精彩场面.
生1:我运用了斜率法.
过程如下:

x0x+y0y=r2
①
当x0=0时,易知切线方程为y=r(或y=-r)满足①式;当y0=0时,易知切线方程为x=r(或x=-r),同样满足①式.
综上所述,过点M的切线方程为x0x+y0y=r2.



图1
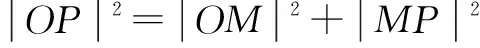

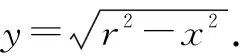
从“高考母题”这一探索点开始,学生展开了思考和探究,学生的思维从被动转变为主动,从一般性策略到创意求解方法,灵活地运用向量、导数等相关知识.正是由于为学生创建的深度思考的氛围,才能让学生在不断探索中拥有无穷的思维创造力,这对提升学生的思维品质和数学核心素养意义重大,同时有效地沟通了多个知识点,实现了知识间的有机融合,进而达到完善自身认知体系的目的.
3.2 善用“高考母题”,一题多变
倘若仅仅是就题论题式解答,既使求解过程再完美,也不过是掌握了一个问题,但一题多变的训练有助于消除这一弊端.所谓的一题多变并非若干个独立题目的简单堆砌,而是具有内部关联的多个习题,意在激发学生的探究兴趣,开拓思路,深化学生对基础知识的理解,培养解题能力.因此,一轮复习中教师应不拘泥于一道习题,活用典型问题,进行深入剖析和精细设计,做到一题求变,将高考母题拓展为多个值得学生探究的数学问题,让高考母题真正成为学生思维拓展的有效素材.这样,不仅可以让知识更加透彻,还能开阔学生的解题视野,更重要的是能提高一轮复习的效果.
例2线段AB的长为2a,且其两个端点A,B分别在互相垂直的两条直线上滑动,动点M为AB的中点,试求点M的轨迹.
经过讨论和交流,学生很快探究得出本题的解法,更进一步地,笔者设计以下变式:

变式2线段AB的长为2a,且其两个端点A,B分别在夹角为θ(0<θ<90°)的两条直线上滑动,动点M为AB的中点,试求点M的轨迹.
复习课无法回避“炒冷饭”的尴尬局面,而如何在“翻炒冷饭”的过程中调动学生的思维,为“冷饭”增添新的“佐料”,让旧知识“炒”出新意,让学生在一轮复习中保持热情是教师的重要关注点.本例中,教师善于以“变”促学,让变式问题不断上升,使学生兴趣盎然.通过解决变式,有助于学生在一轮复习中将基础知识形成网状知识结构,内化为自己的基本技能,感悟数学思想方法,同时还可以提高学生的自主探究能力.
3.3 善用“高考母题”,一题多用
学生听懂一道习题并不意味着掌握,真正的掌握应该是利用此问题的解法去解决新的问题,也就是实现一题多用,这才是真正意义上的领悟和掌握.因此,在一轮复习中,为了实现触类旁通,在探究和解答完高考母题之后,还需引导学生站在研究和剖析的角度审视问题,进一步回顾、总结和提炼,从而深化认识,提高复习效能.
例3试求出平面内到两个定点的距离之比为2的动点M的轨迹方程.(具体解答过程略.)
本题推广引申后,可得如下命题:平面内到定点A和B的距离之比为定值λ(λ>0,λ≠1)的动点的轨迹是一个圆.(这就是著名的“阿波罗尼斯圆”,这一结论就是阿波罗尼斯轨迹定理,这一问题频繁出现于近几年的高考试题之中,可见,是高考热点问题之一.)
进一步地,笔者提出以下问题:

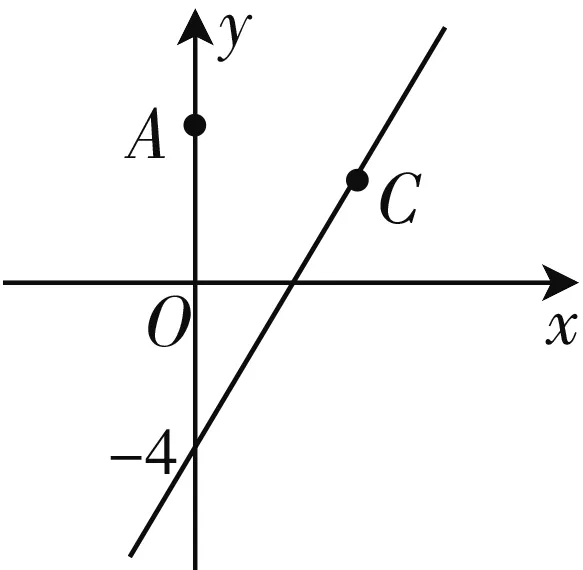
图2
问题2如图2,已知平面直角坐标系xOy中,直线l:y=2x-4,点A(0,3).设圆C的半径为1,且圆心C在直线l上.若圆C上存在一点M使得|MA|=2|MO|,试求出圆心C的横坐标a的取值范围.
问题1和问题2背景相差甚远,但题目中均涉及到“阿波罗尼斯圆”,这一知识点是解题的突破口.正是由于之前的总结和提炼,学生可以很快突破难点,寻得解法,灵活运用相关知识点解决问题.
4 总结
总之,一轮复习的主要目标是夯实基础,提升能力.教师只有切实精心准备,以具有代表性的“高考母题”为指引,在深度和广度上下足功夫,实施一题多解、一题多变、一题多用,才能让学生真正做到做一题会一类,做一类通一法,才能帮助学生构建知识体系,提高思维能力,达到真正提高一轮复习效果的目的.

