交换环上的w-弱平坦模与w-弱内射模
宋菲菲,乔 磊,夏伟恒
(四川师范大学 数学科学学院,四川 成都 610066)
0 引言
本文恒设R是有单位元的交换环,且所有模都是酉模.众所周知,平坦模与FP-内射模(也称绝对纯模)是模范畴理论和同调理论中重要的模类,对凝聚环的刻画发挥了重要作用[1].2015年,Gao等[2]利用超有限表现模引入了弱平坦模和弱内射模的概念,并把凝聚环上的一些结论推广到了任意环上.需要指出的是,弱平坦模和弱内射模的概念与Bravo等[3]引入的FP∞-内射模(绝对clean模)和level模的概念是等价的.
1997年,Wang等[4]介绍了整环上相对于w-算子的平坦模,即w-平坦模,这里要求w-平坦模是无挠模.随着Yin等[5]把整环上的w-模理论推广到一般交换环上,w-平坦模的概念也被Kim等[6]推广到了一般交换环上.此后,Wang等[7]利用w-平坦模刻画了VN正则环,Wang等[8]引入了模的w-平坦维数和环的w-弱整体维数.
2018年,Xing等[9]引入了绝对w-纯模,并利用绝对w-纯模刻画了VN正则环.2021年,Wang等[10]引入w-FP-内射模,并研究了模的w-FP-内射维数与环的整体w-FP-内射维数.在凝聚环下,w-FP-内射模与绝对w-纯模是等价的.本文对经典的弱平坦模和弱内射模进行w-模化理论研究.首先引入w-弱平坦模和w-弱内射模的概念,并讨论它们的基本性质;其次,研究模的w-弱平坦维数和w-弱内射维数,给出它们的一些等价刻画;最后,讨论环的w-超有限表现维数.
1 预备知识
设J是R的有限生成理想,若自然同态φ:R→J*=HomR(J,R)是同构,则称J为R的Glaz-Vasconcelos理想,简称GV理想(相关概念与记号参见文献[5]),并记J∈GV(R).
设M为R-模,记torGV(M)={x∈M:存在J∈GV(R)使得Jx=0},则有torGV(M)是M的子模,称torGV(M)为M的完全GV-挠子模.特别地,若torGV(M)=M,则称M为GV-挠模.若torGV(M)=0,则称M为GV-无挠模.

设M是GV-无挠模,令Mw={x∈E(M):存在J∈GV(R)使得Jx⊆M},则Mw称为M的w-包络,其中E(M)是M的内射包.可以看到,GV-无挠模M是w-模当且仅当Mw=M.设f:M→N是R-模同态.若对R的任何极大w-理想T,fT:MT→NT是RT上的单同态(满同态或同构),则f称为w-单同态(w-满同态或w-同构).设A→B→C是与R-模同态的序列.若对R的任何极大w-理想T,AT→BT→CT是RT上的正合列,则称A→B→C为w-正合列[13].
对w-正合列A→B→C→0及任何R-模M,若诱导序列0→M⊗RA→M⊗RB→M⊗RC→0仍是w-正合列,则称序列0→A→B→C→0为w-纯正合列.特别地,若A是R-模B的子模,且序列0→A→B→B/A→0是w-纯正合列,则称A为B的w-纯子模[14].设A是R-模,如果A是每个R-模中的w-纯子模,其中包含A作为子模,那么A称为绝对w-纯模[9].


设X是R上的未定元,令
Sw:={f∈R[X]:c(f)w=R},
其中c(f)表示多项式f的容度.Sw是R[X]中的乘法集,记R{X}=R[X]Sw,称为R的w-Nagata环.设M是R-模,定义M{X}=M[X]Sw=R{X}⊗RM[1].记M+为M的特征模,即M+=HomZ(M,Q/Z).
2 主要结论
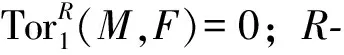
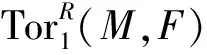

显然,弱平坦模、GV-挠模和w-平坦模都是w-弱平坦模.弱内射模、绝对w-纯模都是w-弱内射模.若R是凝聚环,则超有限表现模与有限表现模是等价的,即w-弱内射模与w-FP-内射模(绝对w-纯模)是等价的,且w-弱平坦模与w-平坦模是等价的.
引理1设T是R的极大w-理想,M是超有限表现R-模,N是R-模,则
证明考虑R-模正合列
0→A→F→M→0,
其中F为有限生成投射模.由M是超有限表现模及文献[18]引理2.3可知,A是超有限表现模.对任何T∈w-Max(R),考虑以下两行为正合列
由文献[1]定理2.6.16(1)可知θ1,θ2是同构.因此,θ是同构. 】
命题1GV-挠模是w-弱内射模.

设A是环,E是A-模.在A×E中定义:
其中r1,r2∈A,x1,x2∈E,则A×E是环,称为A通过模E的平凡扩张,记为A∝E[19].
下面例1说明w-弱平坦模(w-弱内射模)不一定是w-平坦模(绝对w-纯模).
例1设K是域且E是无限秩的K-向量空间,设R=K∝E是K关于E的平凡扩张.由文献[19]定理3.4可知,每个超有限表现R-模是投射的,因此每个R-模是弱平坦(弱内射)的,也是w-弱平坦(w-弱内射)的.由于R不是VN正则环,所以存在一个R-模不是w-平坦模(绝对w-纯模).
弱平坦模(弱内射模)是w-弱平坦模(w-弱内射模),反之不一定成立.下面的例2和例3分别说明了这两个事实.
例2设(R,T)是2维Noether正则局部环(一定是整环),则T是由长度为2的正则序列x,y生成,于是T=(x,y)是GV-理想.故M:=R/T是GV-挠模,从而是w-弱平坦模,但M不是弱平坦模,否则M是GV-无挠模,导致M=0矛盾.
例3设(R,T)是2维Noether正则局部环(一定是整环),则T是由长度为2的正则序列x,y生成,于是T=(x,y)是GV-理想.故M:=R/T是GV-挠模,从而是w-弱内射模.注意到,R-模N是可除模当且仅当对R的任何非零因子s有N=sN.假设M:=R/T是可除模,取0≠a∈J(R),则M=aM.但M是有限生成模,故由中山引理知M=R/T=0,即R=T.这与T是真理想矛盾,故M不是可除模,从而不是内射模.由于在Noether环下内射模与弱内射模是等价的,因此M不是弱内射模.
命题2(1)设{Mi}i∈I是一簇R-模,则⊕Mi是w-弱平坦模当且仅当每个Mi是w-弱平坦模.
(2)设{Ni}i∈I是一簇R-模,则⊕Ni是w-弱内射模当且仅当每个Ni是w-弱内射模.

(2)类似于(1)的证明,由同构关系
即得(参见文献[1]定理3.9.2(1)). 】
弱平坦模关于直积是封闭的,但对于w-弱平坦模并不成立.文献[20]例2.1说明在Noether环条件下,w-平坦模的直积并不总是w-平坦模,因此w-弱平坦模的直积并不总是w-弱平坦模.
命题3(1)设M是R{x}-模,若M作为R-模是w-弱平坦模,则M作为R-模是弱平坦的.
(2)设T∈w-Max(R),M是RT-模.M作为R-模是w-弱平坦模,则M作为R-模是弱平坦模.
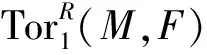
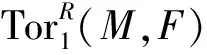
命题4(1)设N是R{x}-模.若N作为R-模是w-弱内射模,则N作为R-模是弱内射的.
(2)设T∈w-Max(R),N是RT-模.若N作为R-模是w-弱内射模,则N作为R-模是弱内射模.
证明证明类似于命题3. 】
命题5(1)若对任何极大w-理想T,有MT是弱平坦RT-模,则M是w-弱平坦模.
(2)若对任何极大w-理想T,有NT是弱内射RT-模,则N是w-弱内射模.
证明(1)设F是超有限表现R-模,则FT是超有限表现RT-模.由文献[1]定理3.4.12有
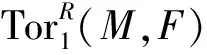
(2)设F是超有限表现R-模,则FT是超有限表现RT-模.由引理1有

引理2[21]设N是R-模.对于正整数n≥1,以下结论等价:
(1)N是n-表示的.
(2)对于正向指标集J上的正向系(Mj)j∈J及每个i 是双射. 命题6(1)w-弱平坦模类关于正向极限封闭. (2)w-弱内射模类关于正向极限封闭. (2)设{Ni}i∈I是w-弱内射模的正向系统.由引理2,对任何超有限表现模F,有 证明(1)M是w-弱平坦模,则对每个超有限表现模F,存在正合列 0→G→Fn-2→…→F0→F→0, (2)与(1)的证明类似. 】 命题8(1)设0→A→B→C→0是R-模正合列,其中C是w-弱平坦模,则A是w-弱平坦模当且仅当B是w-弱平坦模. (2)设0→A→B→C→0是R-模正合列,其中A是w-弱内射模,则B是w-弱内射模当且仅当C是w-弱内射模. 推论1设M是GV-无挠R-模,则M是w-弱平坦模当且仅当Mw是w-弱平坦模. 证明由文献[1]命题6.2.5(2)有Mw/M是GV-挠模,自然也是w-弱平坦模.由短正合列 0→M→Mw→Mw/M→0 及命题8(1)即可得证. 】 定理1设0→A→B→C→0是R-模w-正合列,其中B是w-弱平坦模.若0→A→B→C→0是w-纯正合列,则C是w-弱平坦模. 弱平坦模的每个纯子模是弱平坦模,弱内射模的每个纯子模是弱内射模[2].w-弱平坦模与w-弱内射模的w-纯子模也有类似的结果. 命题9w-弱平坦模的每个w-纯子模是w-弱平坦的. 证明设A是w-弱平坦模B的w-纯子模,令C=B/A,则0→A→B→C→0是w-纯正合列.由定理1有C是w-弱平坦模,由文献[6]定理3.2有w-正合列 命题10w-弱内射模的每个w-纯子模是w-弱内射的. HomR(F,B)→HomR(F,C)→0 定义2设M是R-模,记M+=HomR(M,E0),其中E0=∏{E(R/T):T∈w-Max(R)}是GV-无挠内射模,称之为M的广义特征模. 引理3[23]设P是素理想,M是R-模,则MP=0当且仅当HomR(M,E(R/P))=0. 命题11(1)M是GV-挠模当且仅当M+=0. (2)M是GV-无挠模当且仅当M可嵌入到E0的一些直积. 证明(1)若M+=0,则 即HomR(M,E(R/T))=0.于是对任意T∈w-Max(R),由引理3有MT=0,即M是GV-挠模.反之,由文献[1]习题6.22可得. 则θ是一个单同态,因此M可嵌入E0的一些直积. 】 由N,F0是超有限表现的及文献[24]引理3.60可知θ1,θ2是同构,因此θ是同构. 】 证明证明类似于引理4,需要用到相伴同构定理. 】 命题12设M是R-模,则以下结论等价: (1)M是w-弱平坦模. (2)M+是弱内射模. (3)M+是w-弱内射模. (2)⟹(3).由弱内射模是w-弱内射模可得. 命题13设M是R-模,则以下结论等价: (1)M是w-弱内射模. (2)M+是弱平坦模. (3)M+是w-弱平坦模. (2)⟹(3).由弱平坦模是w-弱平坦射模可得. 推论2在凝聚环R上,以下结论成立: (1)M是w-平坦模当且仅当M+是FP-内射模,当且仅当M+是w-FP-内射模. (2)M是绝对w-纯模当且仅当M+是平坦模,当且仅当M+是w-平坦模. 命题14设M是R-模,则以下结论等价: (1)w-wfdR(M)≤n. (4)若序列0→Fn→Fn-1→…→F0→M→0是正合列,其中F0,F1,…,Fn-1是w-弱平坦模,则Fn也是w-弱平坦模. (5)若序列0→Fn→Fn-1→…→F0→M→0是正合列,其中F0,F1,…,Fn-1是弱平坦模,则Fn也是w-弱平坦模. 证明(1)⟹(2).由定义3(i)可得. (4)⟹(5).由弱平坦模是w-弱平坦模可得. 命题15设R是环,N是R-模,则以下结论等价: (1)w-widR(N)≤n. (4)若序列0→N→E0→…→En-1→En→0是正合列,其中E0,E1,…,En-1是w-弱内射模,则En也是w-弱内射模. (5)若序列0→N→E0→…→En-1→En→0是正合列,其中E0,E1,…,En-1是弱内射模,则En也是w-弱内射模. 证明与命题14的证明类似. 】 命题16设0→A→B→C→0是R-模正合列,若w-wfdR(B) 命题17设0→A→B→C→0是R-模正合列,若w-widR(B) 证明与命题16的证明类似. 】 引理6[17]设M是有限表现R-模,则以下结论等价: (1)M是w-分裂模. (2)M是w-投射模. (3)M是w-平坦模. (4)对于R的任何极大w-理想T,有MT是自由RT-模. 命题18对于任何n≥0,以下结论等价: (1)对于所有超有限表现R-模F,有w-sdR(F)≤n. (2)对于所有超有限表现R-模F,有w-fdR(F)≤n. 证明(1)⟺(2).由引理6及超有限表现模是有限表现模知,当F是超有限表现模时,F是w-分裂模当且仅当F是w-平坦模. (1)⟺(3).由文献[17]命题3.3可得. (2)⟺(4).由文献[8]命题2.3可得. 】 设R是任何环,sp.gldim(R)=sup{pdRM:M是超有限表现R-模}称为R的超有限表现维数. 定义4设R是任何环,w-sp.gldim(R)=sup{w-sdR(M):M是超有限表现R-模}称为R的w-超有限表现维数. 引理7[17]设R是环,则以下结论等价: (1)对任何R-模M,pdR(M)=w-sdR(M). (2)对任何R-模M,fdR(M)=w-fdR(M). (3)R是DW环. 定理2若R是DW环,则 w-sp.gldim(R)=sp.gldim(R). 证明由引理7可证. 】 定理3设R是任何环,则 (1)w-sp.gldim(R)≤w-w.gl.dim(R);当R是凝聚环时,w-sp.gldim(R)=w-w.gl.dim(R). (2)w-sp.gldim(R)=sup{w-widR(M):M是R-模}=sup{w-wfdR(M):M是R-模}. 证明(1)假设w-w.gl.wid(R)=n<∞.设M是超有限表现模,则存在一个正合列 0→Pn→Pn-1→…→P0→M→0, 其中P0,P1,…,Pn-1是有限生成投射模,Pn是w-平坦模.由文献[18]引理2.3知Pn是超有限表现模,自然是有限表现模.由引理6知Pn是w-分裂模,因此w-sdR(M)≤n,即w-sp.gldim(R)≤n. 由于R是凝聚环,所以超有限表现模与有限表现模是等价的.由引理7有w-分裂模与w-平坦模是等价的.此时,w-分裂维数与w-平坦维数也是等价的.结合文献[8]命题3.3即可得证. (2)由命题18可得. 】 推论3对任何R-模,以下结论等价: (1)w-sp.gldim(R)=0. (2)每个R-模是w-弱内射模. (3)每个R-模是w-弱平坦模. (4)每个超有限表现模是w-分裂模. 推论3表明,如果R是凝聚环,则可以在w-sp.gldim(R)=0的条件下给出VN正则环的一个刻画.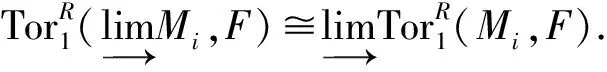








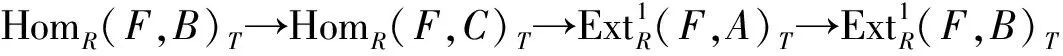
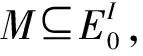


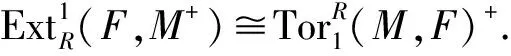
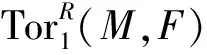


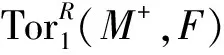


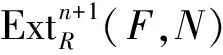





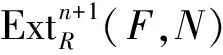
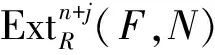


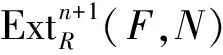

——以指数、对数函数同构问题为例

