Banach空间中时滞发展方程周期解的存在性与唯一性
李永祥,韦启林
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
1 引言与主要结果
在理论和应用中,许多时滞偏微分方程,如时滞反应扩散方程、时滞波方程、时滞Schrödinger方程等均可化为某个Banach空间X中的抽象时滞发展方程
(1)

对不含时滞的抽象发展方程周期问题,其解的存在性已有较深入的研究[2-6].Liu[2]对一般Banach空间中半线性发展方程
u′(t)+Au(t)=f(t,u(t)),t∈R
(2)
在其具有有界mild解的条件下获得了周期mild解的存在性.文献[3-5]讨论了有序Banach空间中T(t)(t≥0)为正C0-半群时方程(2)ω-周期mild解的存在性.李永祥[3]、沈沛龙等[4]在方程(2)具有一对有序的下ω-解v0与上ω-解w0的条件下,应用单调迭代方法获得v0与w0之间最大与最小周期mild解的存在性.李永祥[5]在非线性项f满足适当序不等式条件下,获得了方程(2)ω-周期mild解的存在性与唯一性;Li[6]研究了Hilbert空间中A为正定自伴算子的情形,在f满足与A谱分离条件下获得了方程(2)ω-周期强解的存在性与唯一性.
近年来,时滞抽象发展方程(1)周期解的存在性引起了学者的广泛关注.Liu[7]在一般Banach空间中通过初值问题mild解的有界性和最终有界性获得了周期mild解的存在性;Li[8]研究了A为Hilbert空间中正定算子情形下多时滞发展方程周期解问题,其应用解析半群理论与一个含时滞的积分不等式获得了周期解的存在性与渐进稳定性;Li[9-10]讨论了有序Banach空间中T(t)(t≥0)为正C0-半群时时滞发展方程ω-周期mild解的存在性,文献[9]应用单调迭代方法获得了最小与最大周期mild解的存在性,文献[10]运用正算子半群理论及Leray-Schauder不动点定理得到了方程正周期mild解的存在唯一性与渐进稳定性.
本文讨论一般Banach空间中时滞发展方程(1)ω-周期mild解的存在性.不失一般性,我们假设-A生成的C0-半群T(t)(t≥0)指数稳定,即线性算子A满足下列假设:
(A1)设-A生成X中C0-半群T(t)(t≥0),且存在常数M≥1及ν>0,使得
‖T(t)‖≤Me-νt,t≥0.
(3)
否则,取适当大的常数C,并在方程(1)两边同加Cu(t),然后以A1=A+CI代替A讨论.因为-A1生成C0-半群T1(t)=e-CtT(t)(t≥0),按C0-半群T(t)的指数有界性,C>0适当大时,T1(t)指数稳定.因此我们总假设条件(A1)成立.
设S(t)(t≥0)为X中的C0-半群,若t>0时S(t)为X中的紧算子,则称S(t)(t≥0)为X中的紧半群.
首先对紧半群情形,有如下存在性结果:

(A2)存在常数C0,C1,C2>0,满足M(C1+C2)<ν,使得
则时滞发展方程(1)至少存在一个ω-周期mild解.
当T(t)(t≥0)不是紧半群时,加强条件(A2),可得如下存在唯一性结果:

(A3)存在常数C1,C2>0,满足M(C1+C2)<ν,使得
则时滞发展方程(1)存在唯一ω-周期mild解.
2 预备知识

设h∈Cω(R,X),考虑X中的线性发展方程
u′(t)+Au(t)=h(t),t∈R
(4)
ω-周期解的存在性.假设半群T(t)(t≥0)指数稳定,即满足条件(A1),则由Gelfand谱半径公式及(3)式可得
因此,1为算子T(ω)的正则值,从而I-T(ω)有有界逆算子(I-T(ω))-1,且
(5)
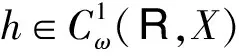
(6)
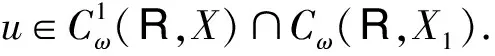

证明对h∈Cω(R,X)及∀t∈R,由(5)及(6)式可得
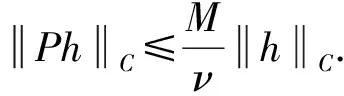
对非线性方程(1),类似于线性方程(4),若u∈Cω(R,X)满足积分方程
(7)


(8)
则方程(1)的ω-周期mild解等价于Q的不动点.我们将对Q应用不动点定理,来获得方程(1)ω-周期mild解的存在性.
3 主要结果的证明

F(u)(t):=f(t,u(t),u(t-τ)),t∈R,(9)

‖F(u)‖C≤(C1+C2)‖u‖C.
(10)
按定义(8),Q为算子线性方程(4)的ω-周期解算子P与F的复合,即
Qu=(P∘F)(u),
(11)

下证Q为全连续映射,即对任意有界的D⊂Cω(R,X),Q(D)在Cω(R,X)中相对紧.
首先,证明Q(D)为等度连续集.令
(12)
对∀u∈D及t1,t2∈R,不妨设t1≤t2,t2-t1<ω,则按(9)与(11)式有
我们分别估计‖J1‖,‖J2‖,‖J3‖.对‖J1‖与‖J2‖,由(10)与(12)式,有
按紧半群的性质,当t>0时,T(t)按算子范数连续.对J3,利用T(t)在(0,+∞)上按算子范数的连续性及积分的Lebesgue有界收敛定理,有
因此与u∈D无关,从而有
故Q(D)等度连续.

(13)
因为Qδ(D)(t)=T(δ)(Q(D)(t)),按Q(D)(t)的有界性及T(δ)的紧性,Qδ(D)(t)在X中相对紧.另一方面,对∀u∈D及t∈R,由(12),(13)式及T(t)在(0,+∞)上算子范数的连续性,并用积分的Lebesgue有界收敛定理可得
因此,对∀ε>0,当δ充分小时,‖Qδu(t)-Qu(t)‖<ε.即Qδ(D)(t)为Q(D)(t)的相对紧的ε-网,因此Q(D)(t)完全有界,从而相对紧.

及Cω(R,X)中的有界凸闭集
D0={u∈Cω(R,X):‖u‖C≤R0},
则对∀u∈D0,由引理1及(10)式,有
因此,Q(D0)⊂D0.由Schauder不动点定理,Q在D0中有不动点u0,该不动点即为时滞发展方程(1)的ω-周期mild解. 】

对∀u1,u2∈Cω(R,X)及t∈R,由(9)式及条件(A3),有
因此
‖F(u2)-F(u1)‖C≤(C1+C2)‖u2-u1‖C.
于是由引理1,有
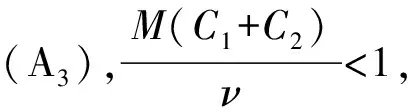
4 应用
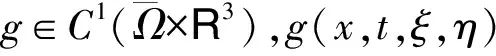
(14)
的时间ω-周期解的存在性.
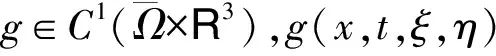
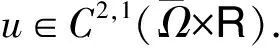
证明取X=Lp(Ω)(p>N),作X中的算子A:

f(t,v,w)=g(·,t,v(·),w(·)),
(17)

例2设g∈C1(R4),g(x,t,ξ,η)关于x与t都以2π为周期.考虑R2中的含有时滞的半线性一阶偏微分方程
(18)
满足双周期条件
(19)
解的存在性,其中a,τ>0为常数.
定理4设g∈C1(R4),g(x,t,ξ,η)关于x与t都以2π为周期.若存在常数C1,C2>0满足C1+C2<α,使得对∀x,t,ξ1,ξ2,η1,η2∈R,有
(20)
则时滞双周期问题(18)~(19)存在唯一解u∈C1(R2).
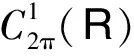
(21)
按文献[5],-A0生成X中的压缩C0-半群T0(t)(t≥0),这意味着对∀t≥0,‖T0(t)‖≤1.因此-A=-A0-aI生成X中的C0-半群T(t)=e-atT0(t),且T(t)满足指数稳定条件(3),其中M=1,ν=a.作g在X中对应的非线性映射f:
(22)


