优化数学活动 促进概念理解
——以二年级上册“角的初步认识”教学为例
浙江杭州市萧山区新塘小学(311200) 朱莹莹
数学课程标准指出,“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。”“教师应激发学生的学习积极性,向学生提供充分从事数学活动的机会……”这给课堂教学提供了一个启示:教师应关注数学活动,以数学活动引导学生观察、思考、实践、交流,真正理解和掌握概念的本质。
一、教材分析
在人教版中,“角”的内容分两次进行学习,分别安排在二年级上册和四年级上册。二年级是初步认识角,感知角的大小,会画角(直角、锐角和钝角)以及能用角的知识解决简单的数学问题。四年级是对角的再认识,在射线的基础上建立角的概念,认识平角和周角,会用量角器量角。
“角的初步认识”这一单元的学习有三个目标:(1)认识角,知道角的特征和各部分名称;(2)画角,从一个点起,用尺子向不同的方向画两条笔直的线;(3)区分角的大小,能通过两条边张开的程度区分角的大小。这三个学习目标都是在帮助学生建立角的概念:目标(1)是从实例中抽象出角的特征,即角由一个顶点和两条边组成;目标(2)既让学生掌握画角这项技能,又让学生通过画角感受角的产生过程;目标(3)让学生感悟角是两条边所夹的部分,角的大小与角两条边张开的程度有关。
二、后测分析
本学期,笔者所在学校的数学组以“角的初步认识”开展教学研究。在一个班的教学完成后,就对这个班进行后测,后测主要是为了了解学生对知识的掌握情况,从而为改进教学提供依据。
1.调查内容的测试与结果
数学组拟定4个题目进行调查,结果如图1所示。
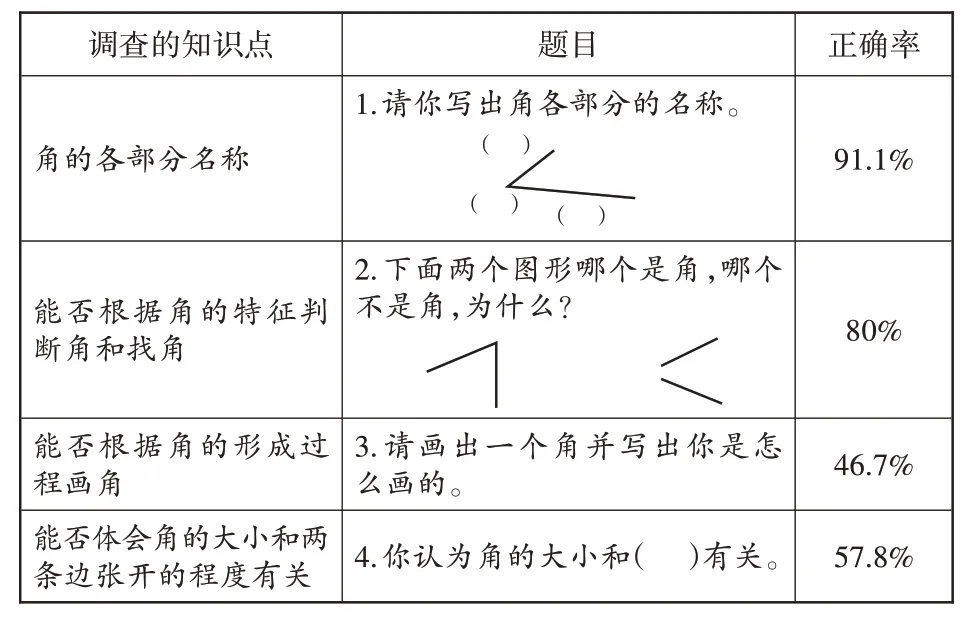
图1
2.调查结果的梳理与分析
(1)从调查结果来看,第1题回答得较理想,只有个别学生因为写了错别字被扣分。
(2)第2题,全班都能正确判断哪个是角,但在判断理由中,有9人认为右图的两条直线没有连接起来,因此它不是角。这说明学生是根据角的表象进行判断的,没有进一步抽象出角的特征。
(3)第3题,学生都能画出角,但细看他们画角的步骤,却发现了很多问题,具体有2种情况。
第一,先画一条线,再画另一条线(如图2)。

图2
第二,先画边再画顶点,而不是按射线延长的方向画(如图3)。

图3
从画角调查的结果来看,这个环节的目标落实不到位。
(4)第4题,只有26名学生认为角的大小与两条边张开的程度有关,有17名学生认为角的大小和边的长短有关,还有2名学生空着。可见,角的大小和什么有关,学生体会不深刻,还需要改进教学。
三、教学思考
“角的初步认识”这一单元属于概念课,概念形成和概念同化是两种基本的概念获得方式。由于二年级学生的认知结构简单、数学知识贫乏,因此他们一般通过概念形成的方式来学习,也就是借助具体的例子和各种数学活动,概括出概念的关键特征。通过教材分析及后测结果分析,我们认为在教学时可以把数学活动做精做细。
1.读懂并用好活动材料
小学生学习数学概念离不开活动材料的支持,尤其是角这个图形。人教版教材中提供了剪刀、钟面和三角尺,细细品味书中给出的几种材料,三角尺是静态的,剪刀和钟面中的角是动态的,后两种通过旋转可以形成任意角,有利于学生感受角的大小和方向。这些材料的选择,为角的概念的学习提供了有效的保障。
2.根据学情调整活动方式
例如,在画角时,可以让学生先思考:画角时,要画出角的什么特征?通过引导学生思考,关注活动重点,让数学活动更有目的性。当然,也可以让学生先画再思考,在反思、交流的过程中掌握画角这一知识点。还可以由教师先示范,学生再模仿。虽然活动方式多样,但教师需要根据学生的学习情况,选择合适的活动方式。
3.根据目标修改活动内容
例如,活动的内容可以来源于学生出现的问题,针对学生出现的问题,教师可设计有效的数学活动,帮助学生解决问题。通过后测发现,体会角的大小是学生认知的难点,在后续的教学中我们将根据教学目标重新设计、修改活动内容,以提高课堂教学效果。
四、教学实践
基于对“角的初步认识”的深入分析与思考,我们对原来的教学设计进行修改,以期可以呈现更好的教学效果。
1.用好活动材料,认识角
二年级学生正处于从以具体形象思维为主向抽象逻辑思维过渡的阶段,因此,数学概念的教学要重视活动材料的运用。
【调整前】
在教学中,教师先呈现剪刀、钟面和三角尺三种材料,让学生找一找角,随着学生的回答,课件直接出现一个角。在后面概括这些角的共同特征时,学生认为尖尖的部分就是角,而直接忽视了两条边的存在。为了增强材料的刺激性,我们在呈现方式上做了调整。
【调整后】
(教师利用课件出示一把慢慢张开的剪刀,形成一个锐角)
师:你能指出剪刀的一个角吗?
(学生上来指其中的一个顶点,但没有指出它的两条边)
师(在黑板上画一个点):角是这样的,你同意吗?怎么指才可以把剪刀中的角完整地指出来?
(学生再次指角,按“顶点→边→边”的顺序指)
(教师利用课件出示一个钟面,分针从12走到了4,形成一个钝角。学生按“顶点→边→边”的顺序指角)
师:这些图形都被称为角,那它们有什么共同特征呢?
在这个环节中,教师将剪刀、钟面中的角动态呈现,使“角”从整体到分步呈现。虽然只是呈现方式的改变,但是却增强了角的“顶点”和“边”的刺激性,将学生的注意力吸引到角共同的关键属性上来。
2.改变活动方式,画好角
【调整前】
师:画一个角,我们要把角的哪些东西画出来?
生1:两条直的边和一个顶点。
师:谁来说一说画角的步骤。
生2:先画顶点,再画两条边。
师:请按照这个步骤试着画一画。
(学生按步骤画角)
学生是学习的主体,教师要做的是如何引发学生的思考,让学生通过自己的探索解决问题。如果教师先示范再让学生模仿,那学生便只是按部就班地画角,至于为什么这么画,学生一点也不理解。基于这样的认识,我们对活动进行了调整。
【调整后】
师:画一个角,我们要把角的哪些东西画出来?
生(齐):两条直的边,一个顶点。
(学生尝试画角)
师:老师收集了两份作业,我们先让这两名同学介绍自己是如何画角的。
生1:我是先画顶点,再从上到下画出一条边,接着从左到右画出另一条边。
生2:我是先画顶点,再从顶点出发画两条边。
师:两名同学的画法不同,你喜欢谁的?
生3:我喜欢生2的,因为他是从一个顶点出发画出两条边的。
师(小结):生1、生2都画出了角的特征——一个顶点和两条边。画角时,我们不仅要画出其特征,而且还要注意画法——从一点开始向不同的方向引出两条直直的线。
活动方式从“教师示范”到“学生尝试”的调整,让课堂更开放,让学生更活跃。通过“要把角的哪些东西画出来”这个问题的引导,将学生的思维聚焦到画角时要画出角的特征,这样的画角尝试更有目标性。
3.调整活动内容,辨角的大小
受生活以及教材中积累的比长短、比面积、比体积等经验的迁移影响,有的学生认为两条边所夹部分“面”的大小就是角的大小,也有学生用两条边的终点连线的长短来判断角的大小。基于这些情况,教师可以设计丰富的体验活动,引导学生体会角的大小。
【调整前】
师:这里有一个角(图略),如果要让这个角变大或变小,该怎么做呢?
生(齐):把两条边拉开,角就变大;把两条边拉拢,角就变小。
师:把两条边拉开,哪里变大了?
生1(指角):角张开的“嘴巴”变大了。
(总结:角的大小与两条边张开的程度有关)
师(出示两个不同的角,图略):刚才我们探究了怎样让角变大变小,现在我们来看看怎么比这两个角的大小。
生2:先将两个顶点叠合,再将其中一条边叠合,最后看另一条边的情况。
师(按照学生说的操作):同学们发现了吗?虽然一个角的两条边长一些,但是张开的程度却没有另一个角的大。因此,角的大小与两条边的长短无关。
调整前,教师出示的两个角除了边的长短不一样,角的大小也不一样。变量多了,学生关注的点就不集中。因此,学生对“角的大小与两条边的长短无关”的体会不深刻。
我们通过课后的访谈得知,很多学生是因为感觉角的两条边拉拢后占的“面积”小了,所以才觉得角小了。这说明学生的“明白”并不是真的明白。在教学中,我们也需要多问“为什么”“你是怎么想的”,以了解学生是否真的明白了。
为了让学生深刻地理解“角的大小与两条边张开的程度有关,与两条边的长短无关”,我们对活动内容进行了调整。
【调整后】
师(出示一个角,图略):如果想让这个角变大,该怎么做呢?
生(齐):把两条边拉开,角就变大。
师:哪里变大了?
生(齐):角的张口变大了。
师:如果想让这个角变小,哪里变小了?
生(齐):角的张口变小了。
师(小结):看来,角的大小是指角两边张口的大小。张口变大,角就会变大,张口变小,角就会变小。请同学们拿出活动角摆出一个角。
师(展示学生摆出的角,如图4所示):这两个角都是直角,比一比谁大?

图4
生1:我认为左边的角大,因为它的两条边长。
生2:我认为一样大,因为它们的张口一样大。
师:怎么证明这两个角的张口一样大?
生2(一边操作,一边说):将两个角的顶点叠合,再将两个角的其中的一条边叠合,两个角的另一条边也是叠合的情况,说明它们的张口一样大。
师(将右边的角放在投影仪上):把这个角放大,现在再和左边的角比一比,谁大?
生4:还是一样大,虽然它的边变长了,但是张口大小没变。
师:如果想让右边的角比左边的大,该怎么做呢?
(学生改变右边的活动角,如图5所示)

图5
在第一次比角中,教师给出的材料是两个一样大的直角,只是边的长短不同。在引导比角的过程中,学生只需要关注一个变量——边的长短,突出了角的大小和边的长短无关。在第二次比角中,教师给出的两个角排除了学生因为角所占“面积”的大小判断角的大小的可能性。两次比角活动,使学生真正理解“角的大小与两条边张开的程度有关,与两条边的长短无关”。
五、效果检测
在调整教学设计后,我们选取了学习水平差不多的班级进行教学,并开展了后测。

调查的知识点角的各部分名称能否根据角的特征判断角和找角能否根据角的形成过程画角能否体会角的大小和两条边张开的程度有关题目1.请你写出角各部分的名称。2.下面两个图形哪个是角,哪个不是角,为什么?3.请画出一个角并写出你是怎么画的。4.你认为角的大小和( )有关。调整前正确率91.1%80%46.7%57.8%调整后正确率90.9%84.1%81.8%77.3%()()()
从后测的数据可以看出,调整后的教学效果比调整前的好,尤其是画角的活动,两次数据相差很大。这些数据告诉我们,数学课要关注数学活动,要向学生提供充分从事数学活动的机会,使学生经历、感受知识的形成过程。
综上所述,在开展数学活动时,为了提高学生的学习兴趣、活跃学生的学习思维,教师可以在活动目标、活动方式、活动内容等方面进行调整,从而提高课堂效率。这种调整值得教师借鉴,因为它确确实实让学生学得更扎实!

