遴选关联评价:“至理数学”视域下大单元新授课教学设计路径
——以二年级上册“乘法口诀”教学为例
江苏南京市栖霞区教师发展中心(210028)陈新涛 张明红
新授课的任务主要是教学新知识、新内容,促使学生完成知识建构,它的特点是“新”,即保证学生有新的收获。在小学阶段,新授课数量最多,以苏教版教材为例,新授课课时约371个,占总课时的一半以上,新授课教学的重要性不言而喻。纵观当下小学数学新授课教学,方法和手段各不相同,实施效果却不尽如人意,究其缘由:一是教师对新授课教学理解五花八门、参差不齐;二是“教、学、评”三者孤立,教学目标、学习任务、评价内容之间缺少沟通和联系;三是教师缺乏全局观念和大单元整体教学设计意识,使得教学碎片化现象严重,同一主题下的课例发力均匀,导致教学重点不突出。基于此,本团队在“至理数学”教学主张指导下,以苏教版教材二年级上册“乘法口诀”教学为例,开展大单元新授课教学实践研究,以探寻新授课教学设计路径。
一、遴选课例,精准定位
1.遴选种子单元
选择“乘法口诀”作为新授课代表开展研究,是因为“乘法口诀”的教学既可看成概念课,也可归为计算课,同时还是同一主题下跨越不同单元的典型课例,有着较强的可迁移性和生长性。然而,在实际教学中,关于乘法口诀的新课课时多(有1~4的乘法口诀、5的乘法口诀、6的乘法口诀、7的乘法口诀、8的乘法口诀、9的乘法口诀等6个课时),且教材内容、结构基本相同,导致教师教得重复、学生学得低效,无法达到创新学习的要求。因此,重新审视教学内容,理解和定位这6个课时之间的内在关联就尤为关键。
学生的认知规律是“整体—局部—整体”,教学内容呈现也应如此。课时设计如同“局部”,大单元、大主题设计如同“整体”。例如,“乘法口诀”是一个大单元、大主题,6个课时中的每一个课时都是它的“局部”,即在理解乘法意义的基础上感受加法和乘法之间的关联,实现教学的整体性和一致性。此外,这6个课时的教材内容、呈现形式和编排结构有很多相似之处,口诀的学习方法和学习经验也具有较强的可复制性。因此,学生完全可以将前面学习乘法口诀的经验自主迁移到后续口诀的学习中,并不断将乘法口诀这一知识系统化、结构化。
2.遴选种子课例
如前所述,“乘法口诀”6个课时的学习方法可以相互影响与迁移。例如,学习1~6的乘法口诀后再学习7、8、9的乘法口诀,学生会感觉比较容易;掌握了乘法口诀含义后,再学习用乘法口诀求商会更加简单。这是因为它们彼此之间有着相似的结构,而小学生的这种迁移能力正是小学数学教学要培养的能力。
为了更好地说明乘法口诀的“前世”“今生”“后续”,下面以图谱的形式表示乘法口诀在整个知识结构中所处的位置以及知识之间的关联(如图1)。
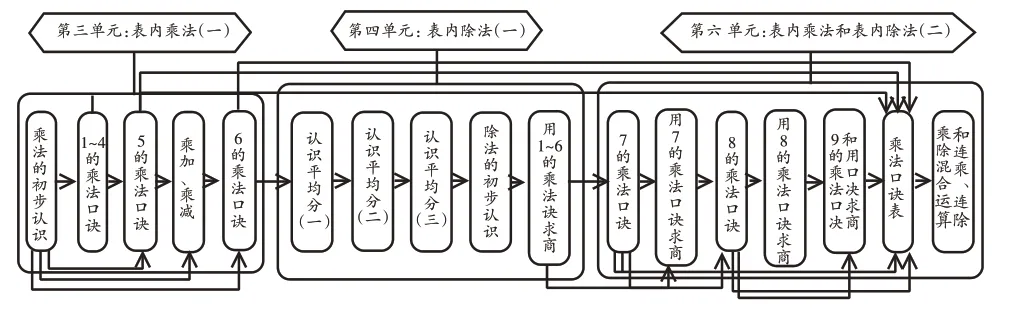
图1 “乘法口诀”相关知识结构图谱
如图1所示,横跨三个单元的“乘法口诀”教学中,“5的乘法口诀”是编排在学生学习“1~4的乘法口诀”之后。因为学生已经具备一定经验,所以“5的乘法口诀”的教学既要基于学生的已有经验,又要为“6的乘法口诀”学法迁移奠基。“7的乘法口诀”在第六单元并作为该单元的起始课,具有承上启下的作用。“9的乘法口诀”是最后一次口诀学习,可以看作前面乘法口诀课的“生长课”,其代表性和特殊性不言而喻。基于此,我们把“5的乘法口诀”“7的乘法口诀”“9的乘法口诀”这三节课作为“乘法口诀”中的种子课来重点研究。
二、关联结构,整体教学
1.板块关联
理学单是落实“至理数学”教学主张的载体之一,主要供学生课堂学习使用。理学单的设计分为横向和纵向两个维度,其中纵向维度有“寻本质·讲道理”和“会关联·能应用”两个栏目。“寻本质·讲道理”重在对新知内容的探究、理解,通过理学单的研究1-1和研究2-1呈现;“会关联·能应用”不仅是对新知学习的巩固和应用,也是对新知学习的关联和评价,对应理学单中的研究1-2和研究2-2。三节种子课的理学单均以四宫格形式呈现(如表1、表2、表3),实现教学设计板块的关联性和一致性。

表1 “5的乘法口诀”理学单

表2 “7的乘法口诀”理学单

表3 “9的乘法口诀”理学单
2.内容关联
(1)自主表征编口诀,讲清数学道理
“至理数学”强调对知识本质来龙去脉的探究,特别要研究知识形成和知识运用背后的道理,帮助学生丰富体验,实现对数学知识的自主解读和整体建构。
如表1、表2、表3所示,“5的乘法口诀”“7的乘法口诀”“9的乘法口诀”三个课时研究1-1中都安排了“编(选)一句乘法口诀,写一写、画一画或算一算”。虽然要求有差异,层次也不同,但都指向让学生自主编写口诀,多元表征对口诀的理解。在“5的乘法口诀”中,学生在之前学习1~4的乘法口诀的经验和基础上,再次借助具体情境感受乘法口诀来自于“几个几”,接着再自主编一句5的乘法口诀,并尝试用自己的方式表征。不同的学生会用不同的方式表达自己的理解,而这一数学理解又会支持学生讲清知识背后的道理。如此设计,不仅尊重了学生学习的自主性和差异性,也让学生将5的乘法口诀编写经验自主迁移到6~9的乘法口诀编写中。正如表2、表3中研究1-1所示,“7的乘法口诀”“9的乘法口诀”教学已经去情境化,促使学生自然迁移已经积累的乘法口诀编写经验。“借助画一画、算一算等数学活动,验证是否正确”的研究任务,目的就是让学生经历讲清数学道理的过程,引导学生个性表征对乘法口诀的检查或验证。不论是画图还是采用连加算式计算,都体现着学生对乘法口诀本质的认识,即“几个几相加”。
(2)二维空间画口诀,加深数学理解
为了帮助学生进一步理解口诀含义,我们在三节课中提供了不同规格的方格纸作为学材,帮助学生在丰富的体验和探究中加深理解。
例如,在表1“5的乘法口诀”的研究1-2环节,学生经历了1~4的乘法口诀学习和研究1-1初步验证口诀之后,再借助6×6的表格继续经历两个层次的学习:一是在方格纸上画乘法口诀,借助图形中的二维空间理解乘法口诀本质,培养乘法口诀记忆的灵活性;二是对比同学的画法,以厘清记忆乘法口诀的几何形体,抽象出不同画法中的相同本质,即乘法口诀的本质是“几个几相加”。此外,还可以通过比较相邻两句口诀的图示,帮助学生主动理解乘法口诀之间的联系(如图2、图3、图4、图5)。

图2

图3

图4
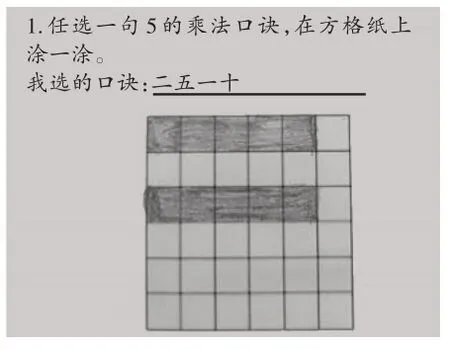
图5
(3)数形结合用口诀,发展数学理性
编口诀、画口诀可以帮助学生有效达成学习目标——对口诀含义的深度理解。但是光理解还不够,运用乘法口诀进行相关计算也是学习目标之一。如表1~表3所示,三个课时的研究2-1环节均设计了运用乘法口诀进行计算的任务,旨在帮助学生在理解口诀含义的基础上灵活运用口诀,达成预期的教学目标。
以“9的乘法口诀”研究2-1为例,借助“任选一句9的乘法口诀,说说它能计算什么算式”,让学生由一句口诀联想若干道与之相关的算式。由于有了学习1~8的乘法口诀的经验,学生思维的发散度很大,学生不仅想到乘法算式,还能想到除法算式、加法算式等。此时,教师可以顺势把学生想到的不同算式以思维导图的方式呈现出来(如图6),通过数形结合的方式帮助学生把不同层次的表达关联起来,从而实现对乘法口诀的多维理解。
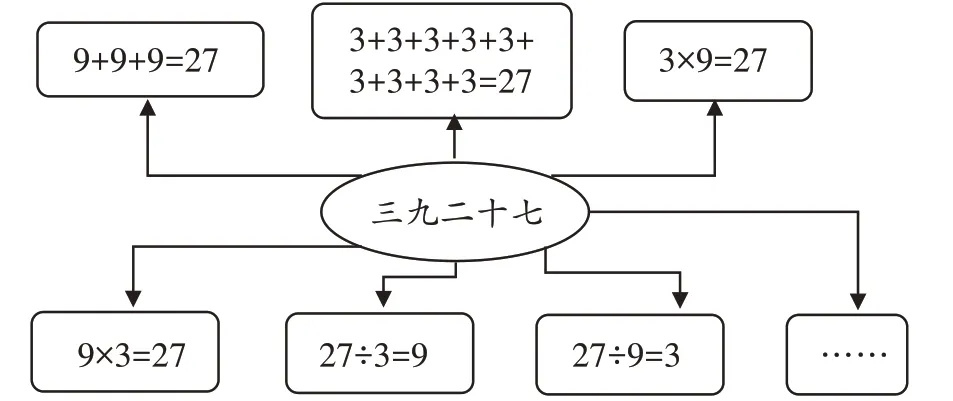
图6
三、评价诊断,“教、学、评”一致
1.课中评价
理学单中研究1-2和研究2-2的内容是对新知学习的关联和评价。表1“5的乘法口诀”理学单、表2“7的乘法口诀”理学单和表3“9的乘法口诀”理学单的研究2-2环节,均设计了根据乘法口诀编实际问题的评价任务,这不仅发展了学生的理性思维和创新精神,还检测了学生对乘法口诀的理解和应用情况,便于教师调控教学。以“7的乘法口诀”为例,因为已经有了用1~6的乘法口诀编实际问题的经验,学生给出的答案大多是用乘法解决的实际问题(如图7、图8);因为在本册教材第四单元“表内除法(一)”中,学生已经学过用1~6的乘法口诀求商,所以也出现如图9、图10所示的答案。这些都表明学生不仅真正理解了乘法口诀的含义,而且能够结合生活实际灵活运用。

图7

图8

图9

图10
2.课后评价
“至理数学”教学主张倡导教师在教学前后均展开学情调研,以便准确了解学生的已有经验、教学起点和学习效果等。其中,课后评价(简称后测)是对已学效果的反馈,也是下一课时的教学参考,利于后续课时的教学调整。例如,教学“7的乘法口诀”后,我们设计了两道题:一是“先把乘法口诀填完整,再写出与它相关的算式”,二是“如果忘记‘四七二十八’中的得数,你会用什么办法想起来”。显然,前者考查乘法口诀的记忆和应用,后者检测乘法口诀的关联情况。

表4 “乘法口诀”单元评价
3.单元评价
“至理数学”视域下的大单元教学评价除了前面提到的课中评价与课后评价,还可以在整个单元学习后进行一次整体评价。与课时评价相比,单元评价的内容应该更多元、更综合,且指向学科关键能力与核心素养。表4是与乘法口诀相关的三个单元教学之后的综合评价,从形式上看,沿用了理学单的“双向四宫格”以呈现基础评价和进阶评价;从内容上看,特别关注演绎推理、归纳对比、概括总结等高阶思维能力的培养。总之,单元评价旨在整体反馈和教学补偿,同时总结经验,以便对其他大单元教学产生正向的影响。
综上,“至理数学”视域下的大单元新授课,要立足大单元整体教学,遴选种子课例,精准把握教学定位,关联孤立、割裂的单课时内容,让知识系统化逐渐走向思维结构化,通过评价诊断教学,最终实现“教、学、评”一致。

