列联表的数据还原算法

李光辉，滕凯敏，赵海清

(1.凯里学院 理学院，贵州 凯里 556011；2.凯里市统计局，贵州 凯里 556001；3.岭南师范学院，广东 湛江 524048)

1 引言

由样本推断总体是统计学的主要工作，通常我们通过抽样调查的方式来收集数据，所获得的这批数据称之为一手数据，或原始数据.将这些数据经过整理归纳分析之后得到的各类统计报表称之为二手数据，其中最为常见的统计报表就是列联表.列表不仅能够显示出一批数据的总体特征，还能探索多个指标之间的相互关系，发掘数据之间内部的联系，直观地体现数据分布的情况.

关于列联表分析的文献有很多，特别是关于独立性检验方面的研究可见文献[1-4]，并且列联表在实际中应用也很广泛，例如文献[5-6]都是基于列联表研究了实际的问题.在列联表分析中也有诸多有趣的问题，例如Simpson悖论[7]等.列联表表现直观，应用广泛，我们也使用列联表研究了关于试验设计方面的问题，特别是构造格点剖分下的均匀设计与均匀性检验方面的问题[8-10].

很多情形下，我们无法获得统计调查的原始数据，而收集到的资料都是零散的各类统计报表.我们希望能从现有的资料中发掘出原始数据的更多信息，或者更进一步，希望通过已有的列联表推断出原始的数据.这样不仅可以基于原始数据进行深层次的分析，而且可以推断出总体的特征，这就是我们希望实现的工作.

常见的列联表主要有2维与3维的列表，3维以上的列联表在各类统计报表中是比较少见的.在一手资料缺失的条件下，现有一批资料，其中共有若干张列表，我们可以看出数据中各项指标之间的关系，而在很多情形下，我们更希望通过现有的列表发掘出更多的信息.这就需要基于现有的列联表对样本数据进行推断，这里就涉及到三个重要的问题：

(1)如何由已知的列联表推断出样本的信息？

(2)如何评价推断结果的优劣？

(3)如何进一步调整推断结果，使之更接近于真值？

本文就围绕这三个问题展开讨论，首先我们定义几个尺度来衡量参数估计的优劣，然后讨论如何求解参数的估计值，由已知的列联表推断出样本的总体信息；进一步以实际的例子来分析讨论.最后提出可进一步研究的问题以及需要改进的地方.

2 列联表数据的矩阵形式

假设我们研究的数据涉及p个指标，称这些指标为p个因子，并将其记为X1，X2，…，Xp.设因子Xi具有li个水平，为方便记，将各水平记作1，2，…，li，i=1，2，…，p.

统计工作者收集到一批样本容量为n的样本，这批数据可以用下表来表示.

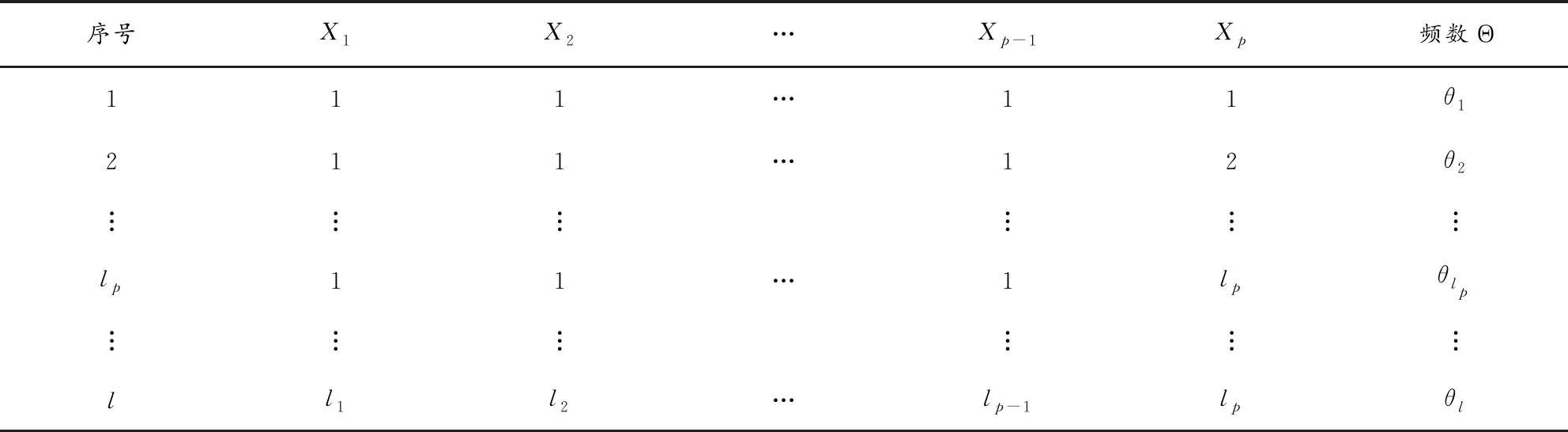
表1 原始数据集

(1)

其中：ni=(1，2，…，li)T，i=1，2，…，p，“⊗”表示Kronecker积，1k是元素全部为1的k维列向量.可见，这里的矩阵

是一个l×p阶矩阵.X中的各行就是因子(X1，X2，…，Xp)在不同水平下的组合，称之为一个“处理”.

由形如表1的原始数据经过整理得到若干张列联表.最为常见的是2维列联表具有如下的形式.

表2 2维列联表(ls×lt列联表)

形如表2的2维列联表，我们也记作ls×lt列联表.在2维列联表中，记

(2)

表示由Xs与Xt形成的2维列联表频数矩阵，我们用记号

表示这批数据中，第s个因子和第t个因子在组合水平a，b下的的频率，也就是

表示的是样本中(Xs，Xt)在水平组合(a，b)下的频数.

C2={T12，T13，…，Tp-1，p}

称为完整的2维列联表集，否则称为不完整的2维列联表集.

对于3维列联表形如以下的形式.

表3 3维列联表(li×lj×ls列联表)

我们将3维列联表记为li×lj×lk列联表.并令

(3)

表示由Xi，Xj与Xk形成的3维列联表矩阵，其中元素如表3所示.同理，用

C3={T123，T124，…，Tp-2，p-1，p}.

由2维和3维列联表可见，样本容量

3 列联表的还原测度

一批资料中有若干张不同的列联表，将这些列联表构成的集合记为C′，并称其为初始列联表集.如果C′中既有2维列联表，也有3维列联表.我们知道，由高维列联表可以推导出低维的列联表和各因子在各水平下的频率.由一张3维列联表可以生成3张2维列联表，以及3张单因子的分布列.单因子分布列可由

得到.3维列联表还可以推导出3张2维列联表

现在的目的是要从现有的资料估计出样本的信息，也就是通过现有的列联表集推断出样本的信息.首先要在C′中剔除多余的列联表.

例如，如果C′中含有3维列联表Tijk，因为Tijk包含了Tij，Tik，Tjk的全部信息，即由3维列联表Tijk可以推导出2维列联表，此时，我们将C′中的Tij，Tik，Tjk剔除(如果有的话)，将此过程描述为以下的定义.

定义1 对于初始列联表集C′，若Tijk∈C′，且{Tij，Tik，Tjk}⊂C′，则将Tij，Tik，Tjk从C′中剔除.经过清理后得到的列联表集记作C，称之为列联表集.

在此，我们定义两个测度，用于度量还原列联表数据的难易程度与精准程度.

为这批列联表集合的完整度.

列联表集的完整度仅仅是定义了2维和3维列联表的完整性，需要注意以下几点.

其次，由前面的讨论可以知道，高维列联表可以推导出低维的列联表，而有的情况下，由若干张低维列联表也可以推导出高维的列联表.最理想的状态是由现有的列联表集推断出表1中的频数值Θ=(θ1，θ2，…，θl)T，这一过程就称之为列联表的数据还原.即使列联表集的完整度α=1，并不一定就能推断出所有组合的准确频数.

的值.

虽然我们无法度量参数估计值与真值之间的偏差，但是希望尽可能的保证估计值的准确度.于是给出下面的定义.

为还原度偏差.

下面我们将介绍求解参数估计的方法.

4 频数的估计方法

设(xr1，xr2，…，xrp)是(1)式中的矩阵X的第r行，xri∈{1，2，…，li}，令yr表示在第r个处理下的频数，它是未知的.这里的行数r可以按照以下方式来确定.

(4)

再设xi=(x1i，x2i，…，xli)T(i=1，2，…，p)是矩阵X的第i列.现在需要根据已有的资料求解出y1，y2，…，yl的值.在列联表集C中，由2维列联表Tst可以确定lslt-1个方程

(5)

由3维列联表Tijk可以确定liljlk-1个方程

(6)

在(5)和(6)中，I(·)为示性函数，且示性函数中的数值与下标满足以下条件

(7)

在条件(7)中有几点是需要说明的.

首先，由于列联表集的不完整性，在方程组中的下标s，t，i，j，k中，仅是标注了它们的值范围，而不表示取遍在此范围内的所有整数.除非列联表集的完整度α=1.

其次，由于列联表集T是由定义1经过整理而得的，所以(7)中任意的(s，t)∉σ(i，j，k)，其中σ(i，j，k)={i，j，k，(i，j)，(i，k)，(j，k)，(i，j，k)}是由元素i，j，k生成数对构成的集合.

最后，在这些方程中，之所以要剔除最后一个方程，即(5)中有(a，b)≠(ls，lt)，(6)中有(a，b，c)≠(li，lj，lk)，这是因为2维列联表和3维列联表的自由度分别是lslt-1和liljlk-1.

若令y=(y1，y2，…，yl)T是未知数向量，定义示性函数向量

I(xi，a)=(I(x1i=a)，I(x2i=a)，…，I(xli=a))T.

方程组(5)和(6)可以记作

(8)

其中“⊙”表示Hadamard积，方程组(8)中的各参数满足条件(7).

进一步，我们对方程组(8)中的每个方程进行编号.

列联表集C中共有n0张不同的列联表，设由C={T1，T2，…，Tn0}中的列联表Tm生成的方程组具有矩阵的形式

Amy=bm，m=1，2，…，n0.

(9)

若Tm是2维列联表，不失一般性，设若Tm对应的是列联表Tst，矩阵Am是(lslt-1)×l阶矩阵，bm是可表示为lslt-1维列向量，即

(10)

若Tm是3维列联表，不失一般性，设若Tm对应的是列联表Tijk，矩阵Am是(liljlk-1)×l阶矩阵，bm是可表示为liljlk-1维列向量，即

(11)

联立两类方程组(10)和(11)，将(8)式记作矩阵的形式，得

Ay=b，

(12)

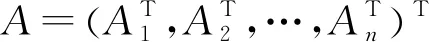
在极少情形下y=(y1，y2，…，yl)T的解是唯一的.并且因为由每个列联表生成的方程组中，我们都剔除了最后一个方程，所以矩阵A的最后一列都是0.也就是说，在大多数情形下，不完整的列联表集推断出的频数估计是不唯一的.在(8)式中，如果

(1)当N=l，且rank(A)=l时，方程(8)有唯一解，但是这种情况非常少，多数情况下是多张列联表推断多因子的数据.例如一张2×2×2列联表恰好还原3因子2水平的数据.

(2)当N>l时，且rank(A)=l，此时求解超定方程(8)，有唯一解，此时方程(8)有唯一解，但不一定能准确的还原数据表1，但是还原度偏差β=0.这种情况也是比较少的.

(3)当N

①AA+A=A；②A+AA+=A+；③(AA+)T=AA+；④(A+A)T=A+A，

并且A+是唯一的.在此我们使用矩阵A的加号广义逆来求解y，y的解可以表示为

y=A+b+(I-A+A)μ，

(13)

由此得到频数的估计，解出y值，令

(14)

5 实例分析

例1 一批3因子2水平的数据，假设各个处理的频数向量为

Θ=(θ1，θ2，…，θ8)T=(2，16，14，10，25，17，25，9)T，

如表4的第5列所示，这些频数值是未知的.如果现有3张2×2的列联表如下

定义未知量向量y=(y1，y1，…，y8)T，根据(9)，(10)，(11)式可以写出矩阵A与向量b分别为:

表4 3张2×2的列联表的估计结果

现在有6张2维列联表分别是

有的情形下，当列联表中的因子与对应的水平都较多时，计算大型矩阵的广义逆是存在困难的.对比例1与例2就可以发现，随着水平数的增大，计算的精度会随之骤降.如果我们关心的是重要的处理下的频数估计，根据文献[12]中更新的正交表，计算在对应处理下的频数估计.文献[13-15]中涉及到了正交表的应用，可以事先将(12)中对应的列联表集中未包含的处理剔除，估计出正交表中对应的处理的频数即可.

6 讨论

由于本文是基于原始数据缺失的情形下，通过现有的列联表来推断原始数据的结构分布，因此对实际情况来说，还存在着许多有待进一步研究的问题.

首先，由于没有参照标准，我们推断出来的频数估计值，要想评价其优劣，也只能通过现有的列表来评价即还原度.而且尽管还原度偏差β=0也不能说明数据还原无误.

其次，由现有的列联表来推断出的各种处理的频数，然后在此基础上分析样本其他的特征，也肯定是会失真的，如何控制偏差的范围也是有待研究的问题.

再次，由列联表的Pearsonχ2性检验与Fisher精确独立性检验的知识可知，由列联表中的频率值构造的检验统计量具有近似的分布.那么我们自然会想到，能否构造出关于各个处理下频数的枢轴量，以此得到各频数的置信区间.

最后，本文所讨论的问题是理想化的情形，但这类问题却有着很好的实用价值，在实际统计工作中经常会遇到类似的问题.如果能很好解决这一问题，对诸多统计工作将会有实质性的帮助.