基于改进MPA 优化的高斯混合模型算法

张长有，张文宇，袁永斌，叶贇瑞

（1.西安邮电大学现代邮政学院，陕西西安 710061；2.西安邮电大学经济与管理学院，陕西西安 710061；3.中国航天系统科学与工程研究院，北京 100854）

1 研究背景

近几年，聚类分析已成为进行数据挖掘的重要工具。根据样本数据的特征，聚类的目的等，聚类方法大致分为以下几类：基于划分的聚类、基于密度的聚类、基于层次的聚类、基于模型的聚类、基于图的聚类等［1］。高斯混合模型（gaussian mixture models，GMM）是一种基于模型的聚类方法，每个簇内的样本数据都被假定为服从某个高斯分布，并且整体的数据分布假定为多个高斯分布按照一定权重进行混合［2］。由于GMM 的数学严谨性以及方法的可行性，GMM 聚类正逐渐应用于各个科学领域，如图像处理、对象识别、信号处理等［3-5］。

通常采用最大期望（expectation-maximization，EM）算法对GMM 的极大似然函数进行求解，从而实现对参数进行估计。EM 算法对初始参数极为敏感，初始参数的好坏直接影响到收敛速率以及是否能得到全局最优解，因此导致GMM 聚类结果波动很大，很大限制了GMM 算法的应用。针对这一问题，许多学者提出了相应的解决方案。Jeffrey 等［6］提出使用bootstrap 结合EM 算法避免算法陷入局部最优。为了防止陷入局部最优和降低初始参数的敏感程度，Reddy 等［7］提出了基于TRUST-TECH 的期望最大化算法。王卫东等［8］提出使用DPC 算法初始化参数，同时令相对熵作为算法的迭代终止条件，提升聚类效果。目前将群智能优化算法与GMM 算法结合的文献较少，而群智能优化算法进行参数优化的研究又是当下研究的热点之一，因此本文将改进的海洋捕食者算法和GMM 算法相结合，避免算法陷入局部最优，提高聚类精度。海洋捕食者算法（marine predators algorithm，MPA）是Faramarzi 等［9］人引入的一种新的自然启发式元启发式算法，具有搜索速度快、全局搜索能力强等特点。但是，MPA 也存在着缺乏对搜索空间的广泛探索、无法快速跳出局部最优等不足。因此，诸多学者对MPA 算法进行了改进，如陈龙等［10］提出基于Tent混沌序列的MPA算法，实现了初始种群的多样化；Fan 等［11］人在MPA 的基础上引入了种群自适应更新策略，提高算法的搜索能力。

因此本文提出一种基于改进的MPA 优化的GMM 聚类算法，首先引入混沌变量代替随机变量初始化种群，同时采用伪反向学习策略，使初始种群更加均匀分布在解空间；其次，引入非线性收敛因子来平衡算法全局和局部搜索过程；同时借助灰狼优化的思想，采用融合等级制度的位置更新策略，提升算法的全局搜索性能。通过对4 个测试函数的实验仿真结果表明，改进的MPA 算法具有更快的收敛速度和更强的寻优能力。将改进的MPA 算法与GMM 算法结合，利用改进MPA 算法的搜索能力，以聚类评价指标作为适应度函数［12］，实现对GMM 初始化参数进行优化，解决GMM 算法对初始参数敏感问题。最后，在4 个UCI 数据集上的实验证明，新的GMM 算法具有更高的聚类精度。

2 相关算法

2.1 GMM 算法

GMM 算法是一种概率式的聚类算法，属于生成式模型。GMM 假定所有的数据样本都是由某个给定参数的多元高斯分布所生成的。给定类个数K，对于给定的样本数据X，GMM 的概率密度函数是由K个多元高斯分布组合而成，其定义如下［13］：

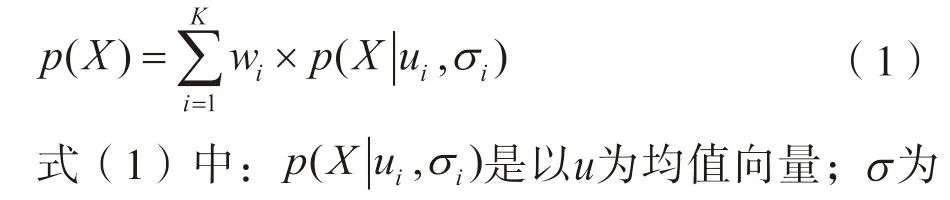
步骤1：根据给定的K值，初始化K个多元高斯分布的均值和协方差矩阵以及其权重w；

步骤2：根据贝叶斯定理，估计每个样本由每个多元高斯分布生成的后验概率；

步骤3：根据步骤2 得到的后验概率计算新一轮迭代的均值、协方差和权重；

步骤4：重复步骤2 和步骤3，直到似然函数增加值已小于收敛阈值，或达到最大迭代次数。

当参数估计过程完成后，对于每一个样本点，根据贝叶斯定理计算出其属于每一个簇的后验概率，并将样本划分到后验概率最大的簇上去，最终实现对样本点的聚类。

2.2 海洋捕食者算法

海洋捕食者算法是一种新提出的群智能优化算法。MPA 的灵感来源于海洋捕食者和猎物之间的生物相互作用，即捕食者根据猎物密集度的高低使用布朗运动或Lévy 运动进行觅食。同时，除了猎物对捕食者的影响之外，涡流形成或鱼类聚集装置（FADs）的影响也是改变捕食者行为的因素之一。MPA 算法的优化过程如下：

（1）初始化阶段。根据式（3）在解空间的上界和下界之间定义具有n个成员的初始猎物种群。

3 算法改进

本文针对GMM 聚类算法对初始参数敏感的问题，提出一种基于改进MPA 优化的GMM 聚类算法。采用改进的MPA 算法对GMM 的初始参数进行优化，实现聚类精度的提高。

3.1 改进的海洋捕食者算法

针对MPA 算法缺乏对搜索空间的广泛探索、无法快速跳出局部最优等问题，提出如下的改进策略从而提升MPA 算法的搜索性能和求解精度。

3.1.1 混沌序列和伪反向学习策略

对元启发式算法而言，初始种群的好坏影响着算法的收敛速度与求解质量。原始MPA 算法使用随机变量初始化种群，由于随机性无法使初始种群均匀分布在解空间的各个区域，因此在初始化种群时，应尽可能使种群均匀分布在解空间中，保障种群的多样性。本文提出一种基于混沌序列和伪对立学习策略的初始化方法，提高初始种群质量。

（1）Circle 混沌序列。混沌序列存在于动态和非线性系统中，具有非周期性、非收敛性和有界性。因此由于混沌序列的动态行为，在元启发式算法中使用混沌变量代替随机变量能有助于更好地探索空间。图1 表示了分别使用均匀随机变量和混沌变量在范围内生成值的对比效果。

图1 随机变量与混沌变量分布效果对比

从图1 可以看出混沌变量比随机变量更均匀地分布在0 到1 内，具有更好的分布效果。本文采用改进的Circle 映射函数［14］来生成范围内的混沌序列，代替随机变量来初始化种群，尽可能让初始点均匀地分布在可行域的空间里。改进的Circle 映射函数表示如下：

（2）伪对立学习策略。Tizhoosh［15］提出的对立学习策略是一种机器智能新方案，研究结果表明对立解相比初始解接近最优解的概率更高。该策略目前已经在PSO 等智能算法中得到成功应用。对于作用域对称情况，对立解是对初始解进行取反，但是两者函数值相等，此时对立解与初始解效果相同。为了提高对立学习的效果，Rahnamayan 等人［16］引入了伪对立学习策略（QOBL），证明了伪对立解通常比原始解更接近最优解。QOBL 策略表示如下：

本文通过使用混沌变量代替随机变量产生初始化种群，然后基于伪对立学习策略生成对应的伪对立解，通过适应度函数对生成的解进行评估，如果对立解优于初始解，则对初始解进行替换。

3.1.2 非线性收敛因子改进策略

MPA 算法的优化阶段根据捕食者与猎物的速度比分为三个部分，第一部分是算法进行全局搜索的过程，第二部分是进行全局与局部共同搜索，第三部分则是局部搜索的过程。MPA 算法令各个部分进行相同的次数，即三个部分各占总迭代次数的三分之一。但是对于相同的优化问题上增加总迭代次数时，会相应地增加各个部分同等的搜索次数，从而产生不同的中值结果，有时优化效果更好，有时会更差。因此本文提出一种非线性收敛因子策略来平衡全局和局部搜索过程。本文使用如下两种函数：

根据图2 可以看到，在迭代初期，算法有很大概率进行全局搜索，迭代中期则容易执行优化阶段的第二部分，而在迭代后期，有很大概率进行局部探索。

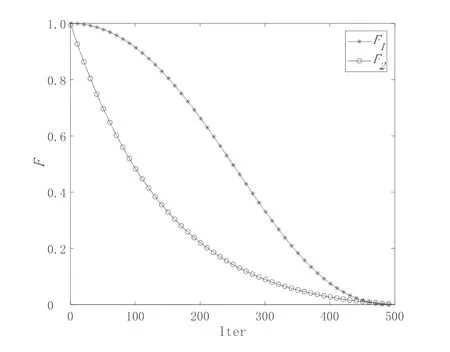
图2 F1 和F2 的变化趋势

3.1.3 融合等级制度的位置更新策略

灰狼优化算法作为一种元启发式算法［17］，模拟了自然界中灰狼的社会等级制度和狩猎过程。算法将灰狼进行等级分层，划分为4 个等级，在位置更新策略中，考虑了狼群的位置信息和狼群最优解、次优解、第三最优解的位置信息，实现了个体与狼之间的信息交换。本文将灰狼优化算法的等级制度融入MPA 算法中，增强捕食者获取猎物的能力，即提升算法的全局搜索性能。

在MPA 算法中，种群的最优个体作为捕食者，本文依据等级制度，将每次迭代前的种群最优个体作为第一级捕食者（α），次优个体作为第二级捕食者（β），适应度值排行第三的个体作为第三级捕食者（δ）。以优化阶段的第一部分为例，此时捕食者不发生移动，猎物进行布朗运动。根据捕食者α、β、δ，其步长计算如下：

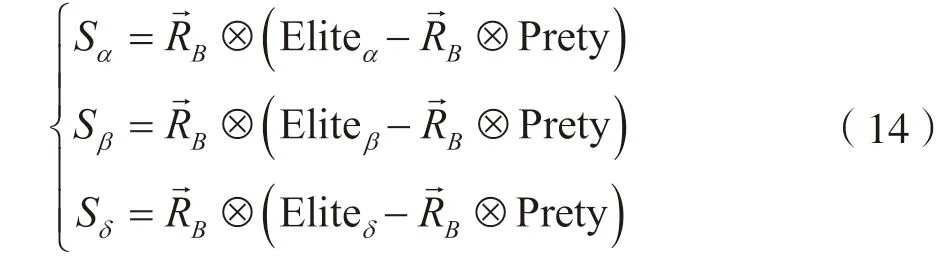
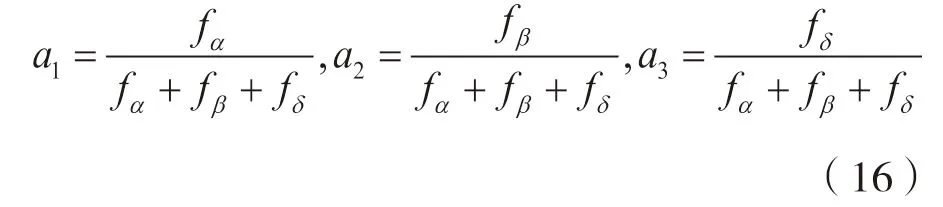
3.1.4 改进的海洋捕食者算法步骤

根据上述的改进策略，改进的海洋捕食者算法（MMPA）的流程图如图3 所示。其实现步骤如下：

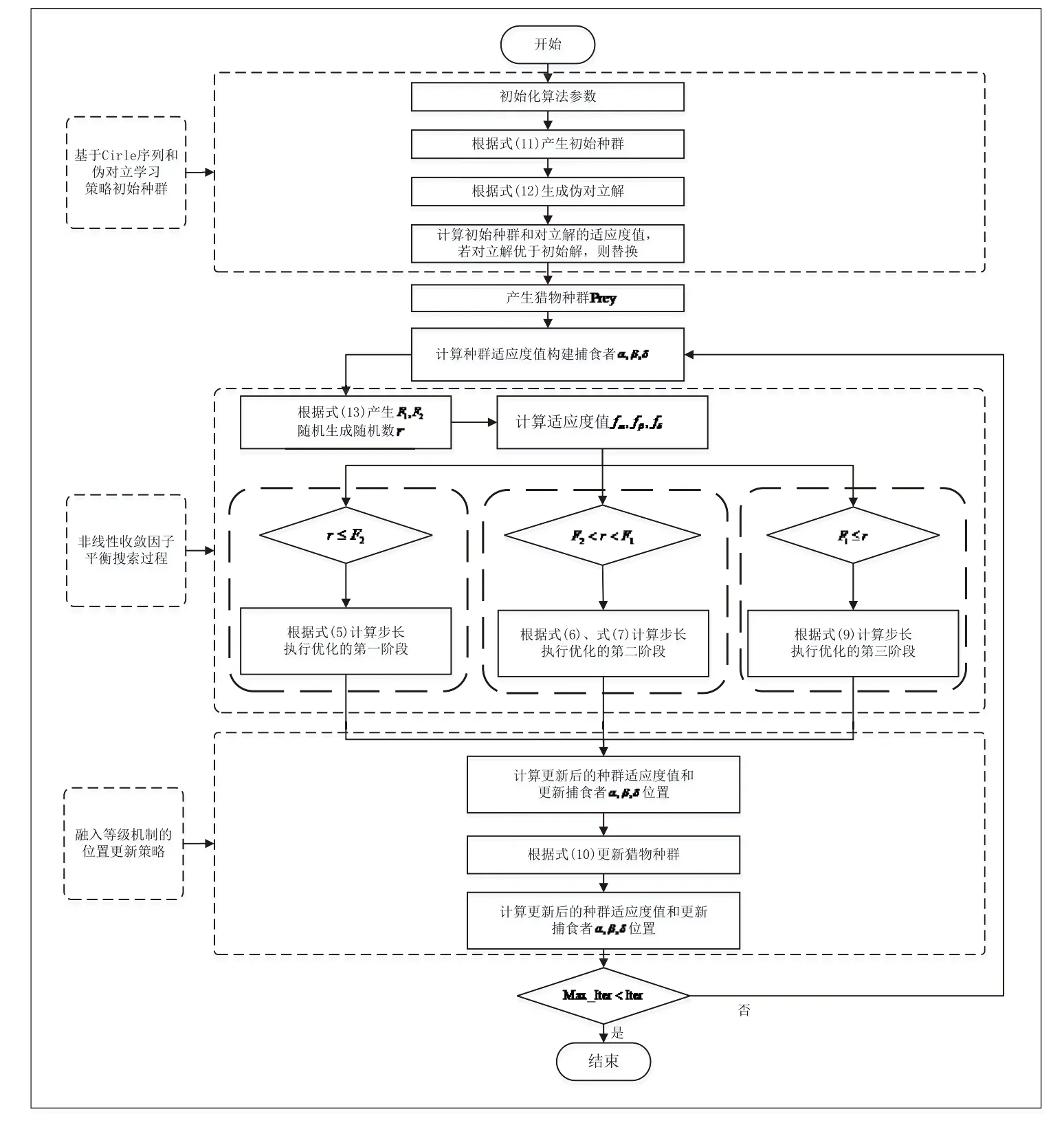
图3 MMPA 算法流程

步骤2：通过式（11）产生混沌序列初始化种群，再根据式（12）生成对应的伪对立解，然后计算初始种群和对立解的适应度值，如果对立解优于原始解，则进行替换；

3.2 MMPA-GMM 算法

3.2.1 算法适应度函数

3.2.2 算法步骤

MMPA-GMM 算法的基本步骤如下：

步骤1：根据给定的聚类数据集，指定其聚类类别数k，数据集中聚类数据的维度数d以及各个维度的最大值与最小值；

步骤6：根据初始化的参数，使用GMM 算法对数据集进行聚类，输出聚类结果。

4 实验结果与分析

实验仿真是在MATLAB2017b 中执行的，使用AMD Ryzen 5 350 0X 6-Core Processor 3.60 GHz 处理器，运行内存为16GB。

4.1 MMPA 性能评估

为了评估MMPA 算法的寻优能力，本文选取4个基准测试函数对MMPA 进行仿真测试，其中包括单峰测试函数和多模态高维测试函数。单峰测试函数常用来测试算法的局部寻优能力，多模态高维测试函数具有许多局部最优值，可以较好地测试算法的全局寻优能力。测试的基准函数如表1 所示。

表1 测试函数相关信息

4.1.1 寻优性能分析

本文通过对MMPA、MPA、GWO、PSO 进行仿真分析，令其分别在各个测试函数上重复运行30 次，得到四种算法在各个测试函数优化上的平均值、标准差、最大值、最小值。各算法的参数设置如表2所示。

表2 参数设置情况

为了更好地测试算法的性能，所有的仿真计算均在同一台计算机中运行。运行结果如表3 所示。

表3 测试结果比较

由表3 可以看到，对于测试函数f1(x)和f2(x)，MMPA 运行30 次的最优平均值分别为2.470e-19 和0.080 4，标准差为2.880e-19 和0.138 2，均远远优于MPA、GWO 和PSO 得到的结果。由于单峰函数具有一个全局最优解，可以测试算法的局部寻优能力，因此基于单峰函数测试结果，可以认为MMPA算法具备更强的局部寻优能力。在多模态高维测试函数仿真中，与其它三种算法相比，不论是求解均值和求解的稳定性上，MMPA 算法都取得了更好的优化结果。而由于多模态测试函数具备许多的局部最优解，因此根据表3 测试结果可以得到MMPA 算法具有更强的全局寻优能力，能较好地在解空间中找到最优解，有效避免陷入局部最优。

从表3 中可以看到，算法在测试函数上运行30次后，MMPA 算法的标准差均小于其余三种算法，说明MMPA 算法与MPA、GWO 和PSO 相比具有更强的稳定性。

4.1.2 收敛速度分析

为了测试MMPA 算法收敛速度，令MMPA 和MPA、GWO、PSO 分别在4 个测试函数上重复运行30 次，得到其收敛次数统计结果。分析结果如表4所示以及各个算法的收敛曲线如图4 所示。

表4 收敛次数比较

由表4 可知，MMPA 算法相比于其余三种算法而言，在4 个测试函数上其平均收敛次数和最小收敛次数都要更小；由图4 可以看到，在相同的迭代次数下，MMPA 算法对比其它算法更快达到了收敛，这也说明MMPA 算法具有更快的收敛速度。

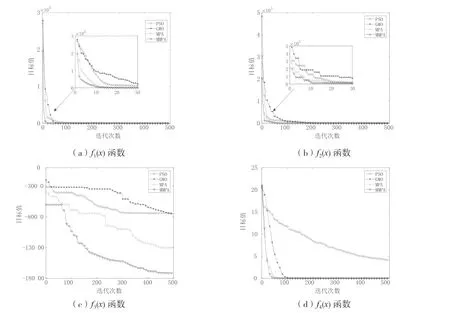
图4 各算法在各个测试函数的收敛曲线

4.2 聚类性能分析

为了验证MMPA-GMM 算法的有效性，本文从UCI 数据库中选取了4 类数据集，分别为Iris、Wine、Seeds、Wdbc 数据集。4 类数据集的相关特征数据如表5 所示。

表5 数据集相关特征

4.2.1 聚类评价指标

本文采用三种聚类评价指标［18］对聚类结果进行分析评价，来验证算法的有效性。这三种评价指标分别为调整的兰德系数ARI、标准互信息NMI 和F-measure 值。指标相关计算如下：

（1）调整兰德系数（adjusted Rand index）：通过计算两个簇之间的相似度来对聚类结果进行评估，ARI 的范围是［-1,1］，值越大，聚类结果与真实情况越一致。

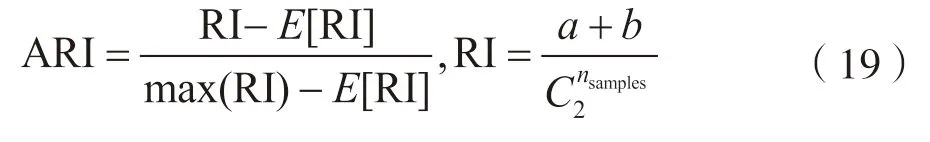
（2）标准互信息（normalized mutual information）：NMI 是度量聚类结果与真实结果之间的相似度指数，如果两者越相似，NMI 值越接近于1，反之接近于0。

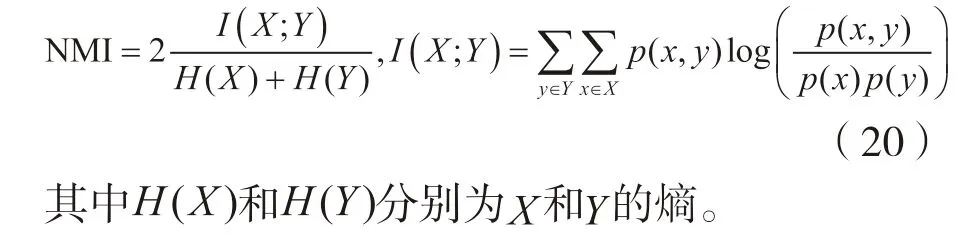
（3）F值（F-measure）：F-measure 是准确率（precision）和召回率（recall）的加权调和平均，是两者的综合度量，更能体现聚类算法的性能。

4.2.2 性能分析

在实验中本文比较了MMPA-GMM、MPAGMM、GWO-GMM、PSO-GMM、GMM 五种算法在4 个UCI 数据集上的性能。设置各算法种群数目为50，最大迭代次数为200。在MATLAB2017b 上仿真分析得到五种算法在数据集上的聚类结果，并计算得到如表6 所示的各个聚类评价指标值。

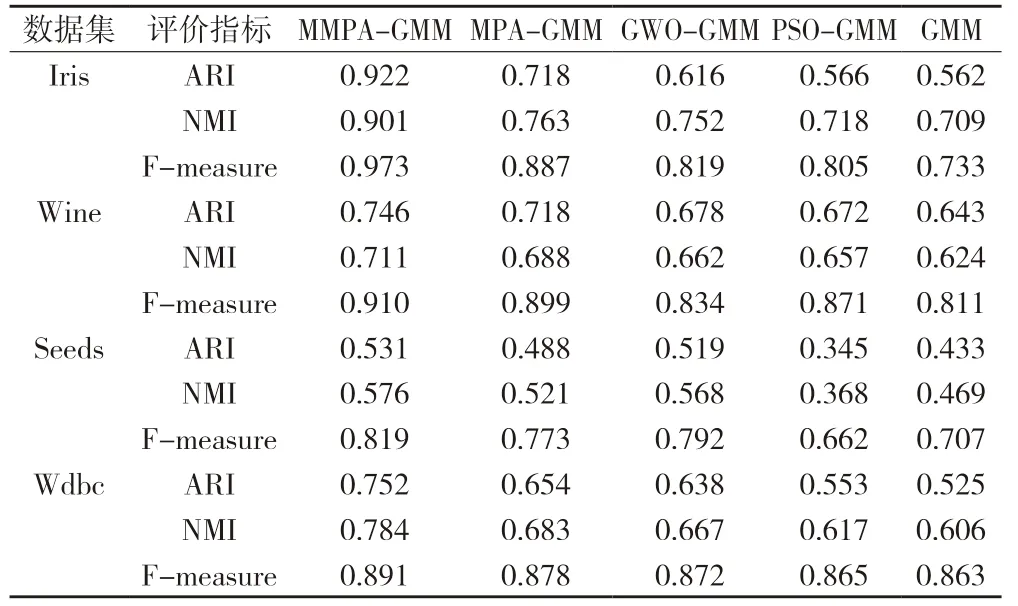
表6 不同算法的聚类仿真结果

由表6 可知，MMPA-GMM 与其它算法相比，在4 个数据集上的聚类效果都更优，其ARI 值、NMI 值以及F-measure 值在各个数据集上都高于另外几种算法。尤其在Iris 数据集上，本文所提出的MMPA-GMM 算法其ARI 值相比于MPA-GMM、GWO-GMM、PSO-GMM、GMM 算法提高了28.4%、49.7%、62.9% 和64.1%，NMI值提高了18.1%、19.8%、25.5%和27.1%，F-measure 值提高了9.7%、18.8%、20.9%和32.7%。结果表明MMPA-GMM 算法相比于其它几种算法的聚类性能更优，能达到更佳的聚类效果。

从图5 可以看到，MMPA 算法相比于MPA、GWO 和PSO 算法在不同数据集上进行参数寻优上都取得了更好的效果，尤其在Seeds 和Wdbc 数据集上，MMPA 最终迭代得到的S_Sbw 指标值明显优于其余三种算法，说明MMPA 算法运行得到的聚类中心坐标使得聚类效果更佳。而且在各个数据集上MMPA算法的寻优速度也优于其它三种算法，在迭代初期就找到了较优的参数，也证明了MMPA 算法的寻优性能。因此可以表明MMPA 算法最终搜索到的参数更优，使得GMM 算法获得了更优的初始化参数，从而令MMPA-GMM 算法聚类性能优于其余算法。

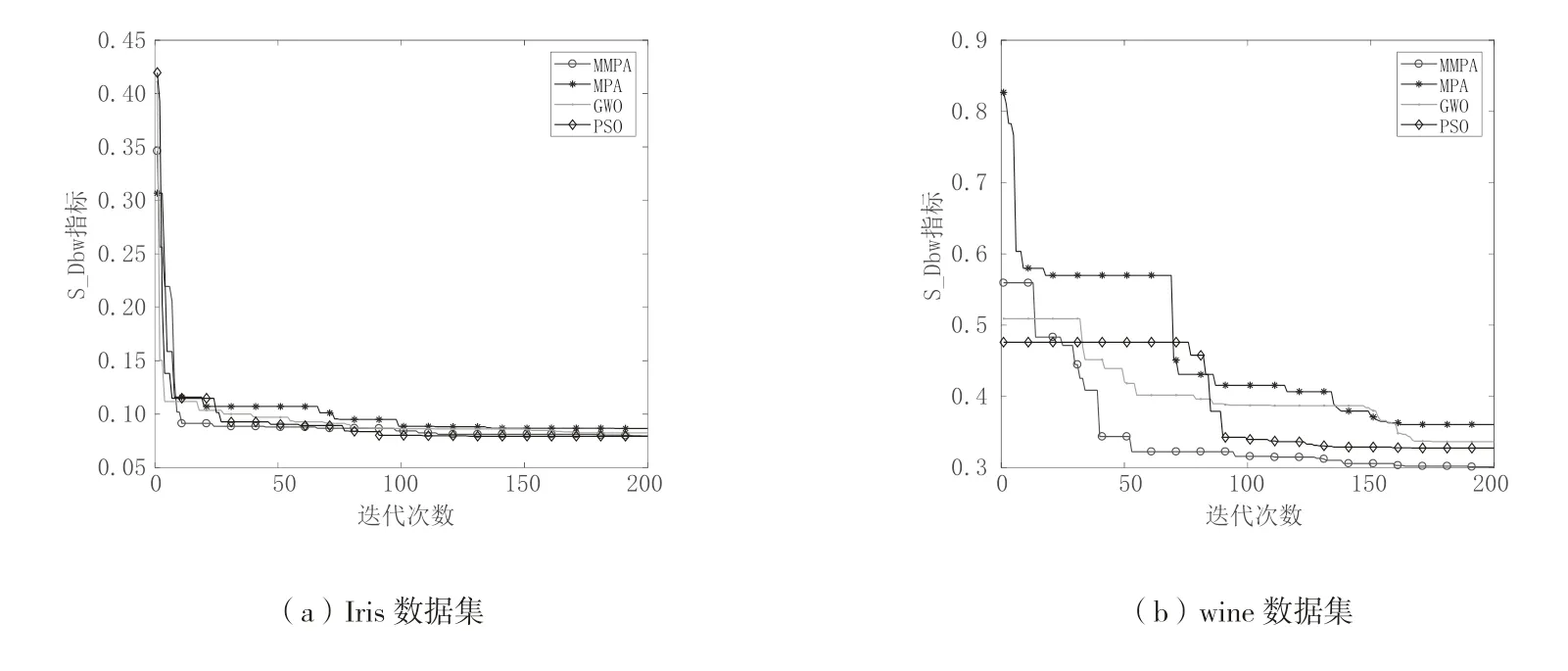
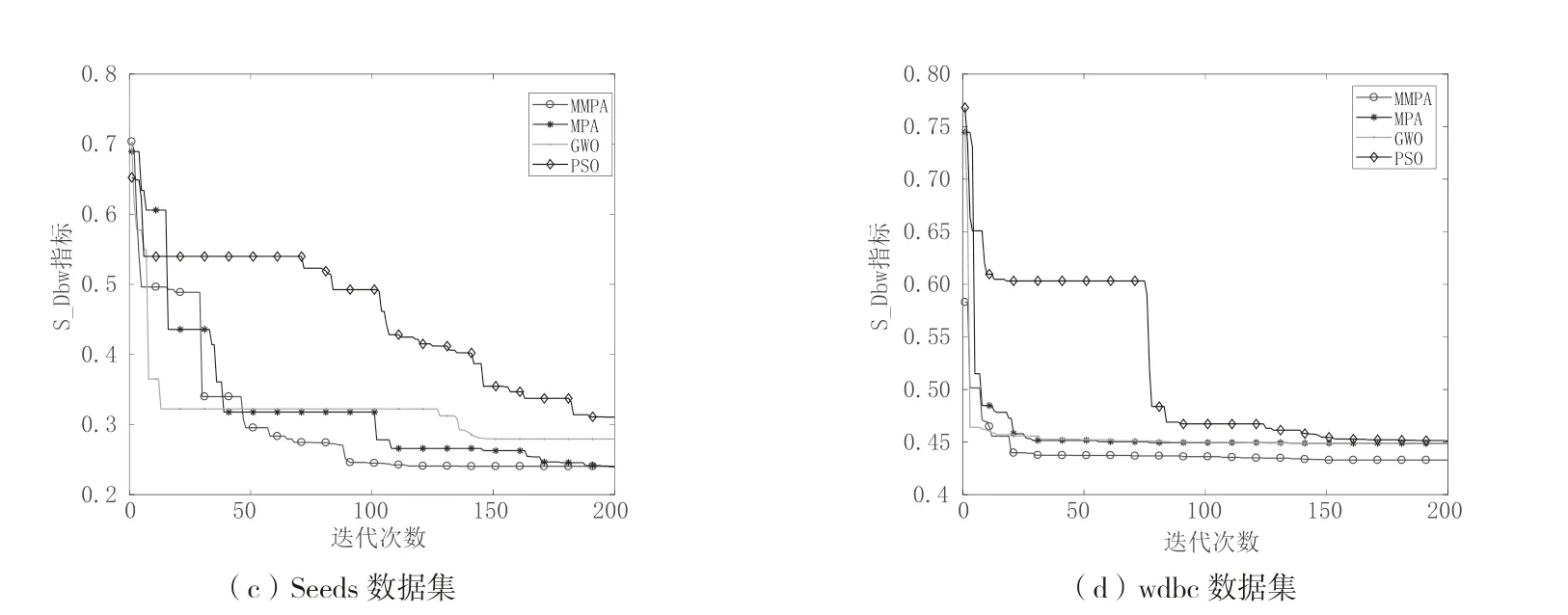
图5 各算法在各个测试集的S_Dbw 变化曲线

4.2.3 稳定性分析

实验将MMPA-GMM、MPA-GMM、GWO-GMM和PSO-GMM 算法分别在4 个数据集上独立运行10次，然后统计四种算法聚类结果的NMI 值，并通过计算各个算法运行10 次后NMI 值的均值和方差作为衡量算法稳定性的指标，验证本文提出的MMPAGMM 算法的稳定性。实验结果如表7 所示，各个算法运行10 次的NMI 值的变化情况如图6 所示。

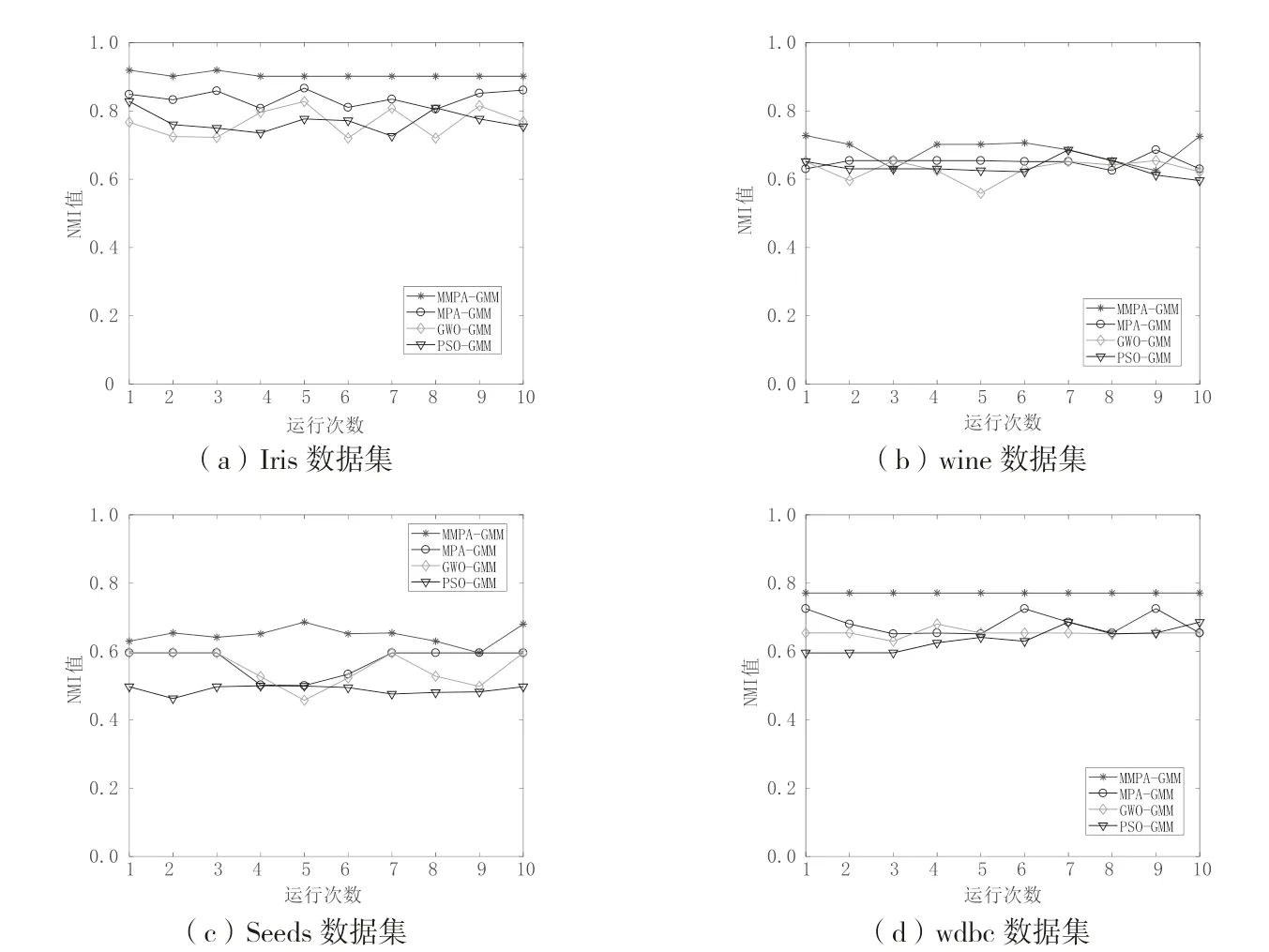
图6 各算法NMI 值变化曲线

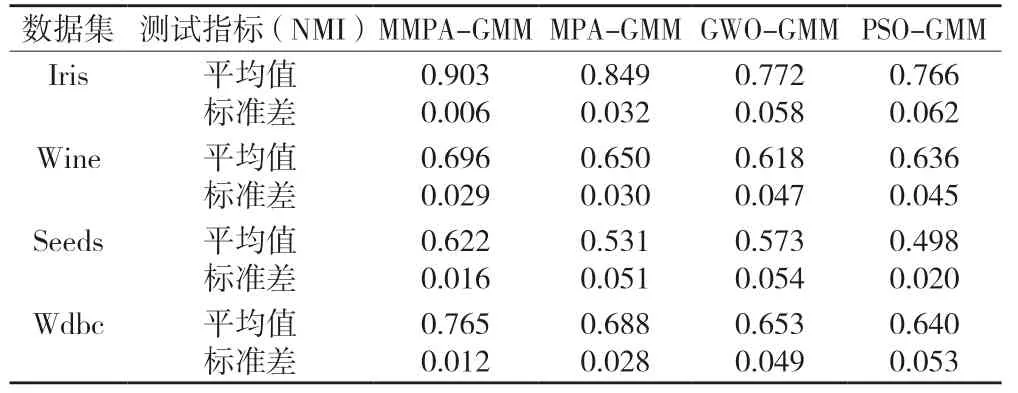
表7 算法稳定性测试结果

由表7 可知，MMPA-GMM 算法在各个数据集上的标准差都低于MPA-GMM、GWO-GMM 和PSOGMM 算法，而NMI 值的平均值都高于其余三种算法。表明MMPA-GMM 算法运行10 次的NMI 值都较为接近，且聚类结果优于另外三种算法，因此可以说明MMPA-GMM 算法在4 个数据集上的稳定性优于MPA-GMM、GWO-GMM 和PSO-GMM 算法。

由图6 可见，MPA-GMM、GWO-GMM 和PSOGMM 算法在四个数据集上NMI 值都出现了一定的波动，而MMPA-GMM 算法在Iris、Seeds、Wdbc 数据集上的NMI 值变化较为平稳，在Wine 数据集上NMI 值变化波动也较小，且在4 个数据集上NMI 值整体高于另外三种算法。综上所述，说明MMPAGMM 算法相比于MPA-GMM、GWO-GMM 和PSOGMM 算法聚类稳定性更高。

5 结论

针对GMM 算法易受初始参数影响的问题，本文提出了一种基于改进海洋捕食者算法优化的高斯混合模型聚类算法。通过在4 个测试函数上的实验结果表明，在单峰和多模态高维测试函数上，MMPA算法都取得了更好的测试效果，改进的MPA 算法与基本MPA 算法、GWO 算法和PSO 算法相比具有更强的搜索能力和更快的收敛速度。然后利用改进的MPA 算法优化GMM 聚类算法的初始化均值和协方差，克服了GMM 算法对初始化参数敏感，易陷入局部最优的不足，从而提高了算法的聚类性能。最后通过在UCI 上4 个数据集上的测试，验证了MMPAGMM 算法相比于MPA-GMM、GWO-GMM、PSOGMM 和GMM 具有更好的聚类性能，能有效避免陷入局部最优。但算法还有较大的提升空间，如何实现对GMM 聚类算法聚类数目优化来提升聚类性能以及算法的实际应用是下一步的研究方向。