基于多尺度有限元模型的海上变电站管轴式吊耳强度分析

吕国儿，何俊生，汤群益，黄珊珊，孙震洲，於刚节

(1.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122；2.三峡新能源南通有限公司，江苏 南通 226400)

0 引 言

海上变电站是海上风电场的关键设施，其可靠性关系到整个风电场的可靠性。变电站结构的上部组块和下部组块一般在陆上分开建造，再分别通过吊装的方式完成海上安装，配备足够强度的吊耳是确保组块顺利完成海上安装的关键。为满足风电场大规模发展的需求，海上变电站结构的尺寸和重量均不断增长，这对海上吊装提出更高的要求。因此，吊耳的强度分析和校核是设计中的重要环节。

关于吊耳强度分析，国内已取得一些研究成果。蔡东等[1]对变电站导管架和上部组块的吊耳分别进行计算分析，验证采用有限元法进行吊耳强度校核的可靠性。吴子昂等[2]对比理论计算与有限元计算的吊耳强度差异，并探讨吊耳板不同布置角度对结构强度的影响。冯加果等[3]研究不同加载方式对吊耳强度计算结果的影响，并推荐沿吊孔孔径方向施加载荷。贠亚杰等[4]在未改变吊耳与其他构件之间装配尺寸的前提下，对船用吊耳板的角度、厚度等参数展开优化。总体上，以往关于海洋平台吊耳强度的研究几乎都围绕耳板式吊耳展开，且运用有限元软件进行分析的思路大多为分2步：(1) 开展梁系结构整体分析；(2) 将整体分析的相关结果经过处理，作为外载荷施加到用ANSYS等软件所建立的吊耳局部模型中。对于边界条件的设置，往往在局部模型的端部施加固定或者简支约束，该简化方法与实际情况有偏差，通常会对计算结果造成较大误差。若对整体模型采用精细化建模的方式，虽会得到相对精确的计算结果，但计算量过于庞大，计算效率过低。因此，建立同时满足计算精度和计算效率的模型对海上变电站吊耳强度的分析具有重要意义。

多尺度有限元是近年来较为流行的分析方法，指在同一个计算模型中既建立高精度的精细单元，又建立高效率的宏观单元，通过一定的方法实现不同单元间的连接，且由于不涉及局部结构的边界条件及其简化处理，通常能达到计算精度与效率的平衡。目前，多尺度有限元被广泛应用于桥梁[5-7]、框架结构[8-10]等领域，尚未有海上变电站吊耳强度校核方面的报道。

本文针对如东海域某大型海上变电站的导管架结构开展其管轴式吊耳强度分析，在SACS软件中建立导管架结构的多尺度有限元模型，即对管轴式吊耳部分进行精细化建模，对其余部分进行宏观建模。同时，在ANSYS软件中建立管轴式吊耳的局部模型以形成对比，分析多尺度有限元模型与局部模型计算结果的差异，并探究筋板设置对吊耳强度的影响，为今后海上变电站吊耳强度的分析和校核提供参考。

1 基本原理

吊耳是海洋工程结构吊装过程中最直接的受力部件，常用的型式分为耳板式和管轴式。耳板式吊耳(见图1(a))主要应用于中小型结构的吊装，规范[11]对于此类吊耳的强度计算方法有明确规定。管轴式吊耳(见图1(b))大多应用于大中型结构的吊装，目前尚无相关规范对其强度计算方法进行规定。

图1 常用吊耳型式示例

按照传统方法，当建立局部有限元模型对吊耳进行强度分析时，通常需先开展基于梁系结构的整体计算，以获得构成吊耳结构每根杆件的杆端载荷，并将其作为外力施加于吊耳局部模型。梁理论一般包括Euler-Bernoulli梁理论(经典理论)和Timoshenko梁理论。对于前者，梁内各点的位移u可用中面挠度ω表示(式(1))，对于后者，梁内各点的位移可用ω和转角φ表示(式(2))：

(1)

(2)

经典梁理论忽略剪切变形的影响，只适用于长梁，不适用于杆件截面高度与长度相比不太小的吊耳局部模型。Timoshenko梁理论对此进行相关改进，即假设变形前垂直于梁中面的横截面在变形后与梁中面存在转角φ，但也仅考虑一阶剪切变形，对于管轴式吊耳局部模型中的短粗梁仍不能精确求解[12]。

根据板壳理论，当结构的曲率半径R与厚度h的比值大于等于20时，可选择壳单元[13-14]。吊耳构件的径厚比为25～35(尺寸信息详见第2.1节)。因此，采用Shell 181单元建立管轴式吊耳的局部有限元模型，该单元既可考虑弯曲和薄膜效应，又可考虑剪切变形，适合对薄板结构到具有一定厚度的壳体结构进行分析，对于线性分析及大转动、大应变的非线性分析均十分适用。

在实际吊装过程中，吊绳仅与管轴壁下侧180°范围内的部分有接触，且吊绳力从其底部向两侧逐渐减小，符合垂向正弦分布规律，用正弦函数[15]可描述为

F=ksinθ

(3)

式中：k为载荷系数；θ为节点角度；F为θ角度处的节点力。

所有节点力的合力等于吊绳力：

(4)

式中：i为接触面上的节点数；P为吊绳力。由式(4)可确定k。

由此得到的局部有限元模型中吊耳垂向正弦分布力的作用如图2所示。

图2 垂向正弦分布力作用

2 数值模型

2.1 工程概况

位于江苏海域的某大型海上变电站下部结构设置2个6柱腿竖直桩式导管架，每个导管架的平面尺寸为12 m×78 m，重约2 000 t，并设置2种类型共4个管轴式吊耳(每种类型各2个)，2种吊耳的构造如图3所示。管轴式吊耳的弦杆采用φ1 700 mm×48 mm圆管(弦杆2)和φ1 200 mm～φ1 700 mm×48 mm锥管(弦杆1和3)，其中圆管段内部均布有6块内径为800 mm、外径为1 604 mm、厚度为48 mm的环形筋板(从左向右编号依次为1～6)，筋板间距为0.8 m。吊耳的撑杆采用φ1 200 mm×36 mm(立面)和φ600 mm×24 mm(水平)圆管。吊耳的管轴采用φ1 200 mm×48 mm圆管，端部用厚度为48 mm的钢板密封。2种吊耳类型的区别仅在于φ600水平撑杆的数量，其余构造均一致。吊耳结构的钢材采用DH36-Z35和DH36，屈服强度为355 MPa，材料密度ρ=7 850 kg/m3，弹性模量E=206×103MPa，泊松比υ=0.3。通过试算，从2种吊耳类型中各自选取其中受力较大的吊耳开展具体研究(即每种类型中各选取1个)。

图3 管轴式吊耳构造示例

2.2 SACS多尺度有限元模型

采用SACS自带的网格划分功能，选中目标节点，并设置网格的形状、尺寸和材料属性。进行网格划分的杆件长度范围如下：水平撑杆1～撑杆3的长度均取3 m，立面撑杆1和撑杆2的长度取2 m，弦杆1和弦杆3(锥管)取其各自端部。软件在上述范围内进行网格划分，最终形成由梁系结构宏观单元和划分网格后的吊耳节点精细单元组成的导管架多尺度有限元模型。SACS软件可自动实现上述2种单元之间的连接，且其网格划分功能可同时实现为目标节点建立不同形状的筋板。多尺度有限元模型中的网格形状采用四边形，其边长定义为0.1 m。2种多尺度有限元模型及其吊耳局部放大模型分别如图4和图5所示。为探究筋板设置对吊耳强度的影响，在上述2种吊耳模型的基础上，分别去除弦杆内部的所有筋板，另外形成一组对比模型。对上述模型开展吊装工况下的结构计算，并重点关注吊耳部分(即精细化网格划分部分)的应力分布情况。

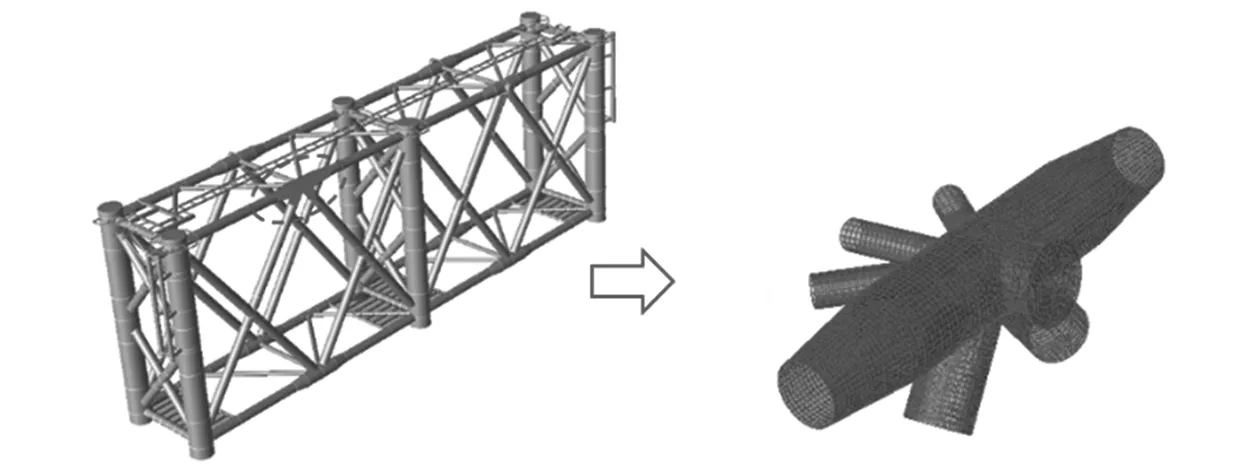
图4 管轴式吊耳类型一

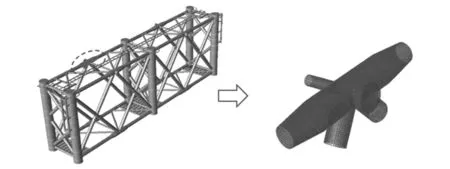
图5 管轴式吊耳类型二

2.3 ANSYS局部有限元模型

建立吊耳的ANSYS局部有限元模型，各杆件的建模长度与多尺度有限元模型中进行网格划分的杆件长度保持一致，并同样采用边长为0.1 m的四边形单元对其进行网格划分。在本研究中，杆端载荷及边界条件的简化需符合圣维南原理和平面假设，即不能显著影响距边界条件较远区域的分析结果。因此，在各杆端形心处建立节点并用link单元将该节点与杆端节点逐一连接，再将从导管架SACS整体模型中提取的吊装工况下计算得到的杆端载荷施加至该形心节点，同时对其施加固定约束。2种管轴式吊耳的ANSYS局部有限元模型如图6所示。同样地，在上述2个模型的基础上去除内部筋板，以形成对比模型。

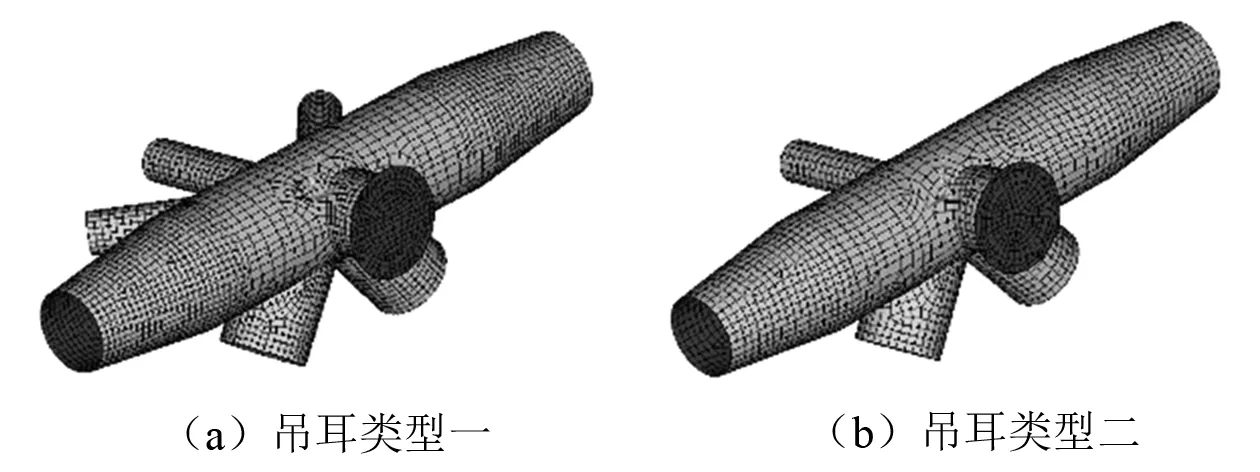
图6 ANSYS局部有限元模型

3 结果分析

3.1 多尺度有限元模型计算结果

多尺度有限元模型的计算结果如图7(无筋板)和图8(有筋板)所示，为更清晰地表示应力(von Mises应力，下同)分布情况，仅给出吊耳局部放大模型。本研究中容许应力比取0.84[16]，则钢材最大许用应力为298.2 MPa。

图7 多尺度有限元模型计算结果(无筋板)

图8 多尺度有限元模型计算结果(有筋板)

由图7(a)可知：吊耳类型一的立面撑杆、管轴与弦杆连接处的小部分焊缝有应力集中现象，最大应力达923 MPa；其次受应力较大的部位为中间横向水平撑杆与弦杆的连接处及与其邻近的弦杆上表面部分区域，应力约250 MPa；圆管段弦杆和立面撑杆的吊耳侧所受应力约200 MPa；吊耳其余部分的应力较小。由图7(b)可知：吊耳类型二应力集中区域的最大应力为841 MPa；其余应力分布规律与吊耳类型一相似。设置筋板后，2种吊耳的应力集中现象均得到消除(见图8)，且均表现为在管轴与弦杆的连接处及立面撑杆的吊耳侧应力较大，分别达298 MPa和295 MPa，在钢材应力的最大容许值之内。此外，吊耳类型一水平撑杆的受力规律表现为两侧斜向撑杆的受力较小，中间横向撑杆与弦杆连接处的应力稍大，为150～200 MPa，与仅有横向水平撑杆的吊耳类型二计算结果相近，表明管轴式吊耳的受力以横向水平撑杆为主，两侧斜向撑杆的设置对整个吊耳的强度变化影响不大。在2种吊耳的筋板中，位于立面撑杆上方的4块筋板承担主要的力，其中距管轴较远的2块筋板(筋板2和筋板5)受力主要集中于靠近管轴侧的下方1/4环，距管轴较近的中间2块筋板(筋板3和筋板4)受力以靠近管轴侧的半环为主。边缘筋板(筋板1和筋板6)受力较小。由于2种吊耳内筋板的应力分布规律类似，以吊耳类型一为例，给出6块筋板的应力云图，如图9所示。此外，该导管架已顺利完成海上安装，表明用多尺度有限元法进行管轴式吊耳的强度计算是可靠的。

图9 筋板应力云图

3.2 局部有限元模型计算结果

局部有限元模型的计算结果如图10(无筋板)和图11(有筋板)所示。

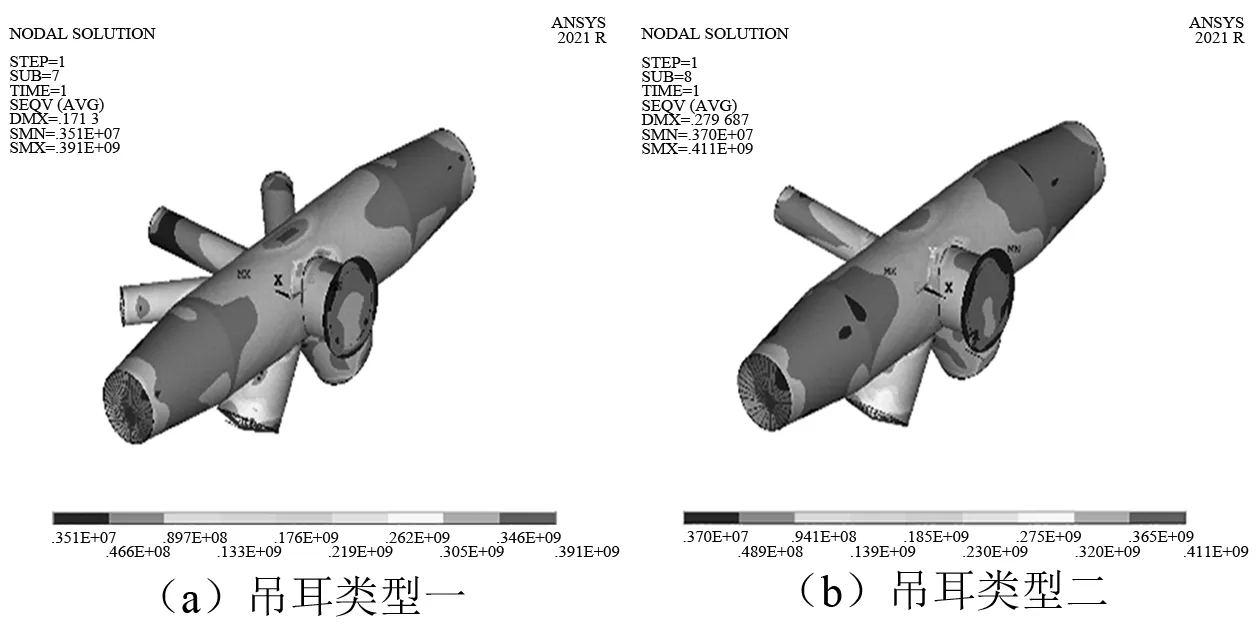
图10 局部有限元模型计算结果(无筋板)

图11 局部有限元模型计算结果(有筋板)

由图10和图11可知，未设置筋板的吊耳均出现与多尺度有限元模型计算结果中类似的应力集中现象，但最大应力分别为391 MPa和411 MPa，远小于前者的最大应力。设置筋板后，应力集中区域的范围有所缩小，但并未消除，且应力未明显改变。此外，筋板设置前后，吊耳弦杆和立面撑杆的端部均存在小范围的应力集中，该现象是由上述杆件较大的端部载荷以及对边界条件的简化处理导致的。局部有限元模型中筋板的应力云图如图12所示。

图12 筋板应力云图

由图12(a)可知，当设置3根水平撑杆时，除筋板1和筋板6应力较小之外，其余4块筋板的应力分布规律与多尺度有限元模型的计算结果相反，即筋板受力以远离管轴侧为主。当仅设置中间横向水平撑杆(见图12(b))时，只有中间2块筋板(筋板3和筋板4)的受力以远离管轴侧为主，其余4块筋板的应力分布规律均与多尺度有限元的计算结果一致。上述现象表明吊耳水平撑杆边界条件的简化处理会导致筋板应力重新分布，使吊耳的强度计算结果与实际有偏差。

4 结 论

对某大型海上变电站管轴式吊耳的强度计算开展研究，探讨吊耳类型、筋板设置对吊耳强度的影响，同时对比分析SACS多尺度有限元模型与ANSYS局部有限元模型的计算结果，得出如下结论：

(1) 多尺度有限元模型计算结果表明，筋板可消除杆件连接处的应力集中现象，且位于立面撑杆上方的筋板承担主要的力，建议在立面撑杆上方设置一定数量的筋板。此外，对水平撑杆而言，吊耳的受力以横向撑杆为主，两侧斜向撑杆的设置对整个吊耳的强度变化影响不大。

(2) ANSYS局部有限元模型计算结果表明，筋板仅缩小应力集中区域的范围，但并未消除，且设置筋板前后吊耳的最大应力未有明显变化，对吊耳水平撑杆边界条件的简化处理会导致筋板应力重新分布。此外，由于杆件端部载荷较大以及对边界条件进行简化处理，弦杆及立面撑杆的端部均存在小范围的应力集中。

(3) 对于管轴式吊耳的强度分析和校核，采用多尺度有限元方法和局部有限元方法计算得到的结果有所差别，且局部有限元方法的计算结果相对更为保守，在设计中应结合工程实际需要和关注的侧重点选择合适的方法。