双前导车影响下高速公路施工路段混行交通流仿真

罗 京, 连 萌，李 伟, 王宝杰

(1.中交第一公路勘察设计研究院有限公司，陕西 西安 710075；2. 深圳高速公路股份有限公司，广东 深圳 518026； 3.长安大学 运输工程学院，陕西 西安 710064)

0 引言

随着我国汽车保有量的增长，居民出行需求不断增加，现有的交通基础设施难以满足当今的交通需求。为提升道路的服务能力，需对其进行升级改造。在施工改造期间，应尽量保证改造路段交通通畅，但施工区仍不可避免地会对交通流产生不利影响。高速公路交通流主要由小汽车和货车组成，其行驶方式因其驾驶员视线高度而不同。在拥堵路段，小汽车跟驰行驶时，只受前方一辆车的影响，即为单前导车影响下的跟驰行为。而货车驾驶员的视线比小汽车高，其跟驰行驶受到双前导车的影响[1]。因此，通过交通流仿真研究双前导车影响下的高速公路施工路段交通流特性有重要意义。

Kesting等[2]提出了考虑最小化车道变换的MOBIL通用车道变换模型来推导车道变换规则。 何民等[3]通过对交通流跟驰模型研究的回顾，评述认为在跟驰模型中存在的问题就是驾驶员可以看到前方不止一辆前导车，而且也会考虑到周边其他车辆和信号灯等交通信息。金春霞等[4]回顾了跟车模型的发展过程，提出跟车的微观模型和宏观模型在仿真中都不可或缺，要结合微观影响建立跟车模型。徐学明等[5]将混合神经网络模型(CNNM)应用于跟驰模型的建立，取得了比单一神经网络模型更好的预测效果。王殿海等[6]通过对车辆跟驰行为建模的回顾，认为跟驰行为建模应该更多地考虑人的因素，如驾驶人的感知阈值、临界安全车头间距等方面。已有众多学者对“小车-大车”混合交通流进行了深入研究[7]。Chanut等[8]基于小汽车和货车的速度差建立了一种混合交通流模型，分析了客货混行交通流宏观特征。Nathan等[9]基于交通流密度，对高速公路基本路段小客车/货车混合交通流中货车对交通流影响的换算系数进行了研究。Wang等[10]采用博弈论模型对车辆换道和跟随模型进行了建模，通过建立成本函数来表示受控车辆与周围车辆之间的相互作用关系。邵长桥等[11]基于实测数据和数值仿真，分析了高速公路改扩建路段的流量及速度特征。吴德华等[12]研究了高速公路因车道减少造成的瓶颈路段的通行能力。在对双前导车交通流稳定性分析方面，廖孝勇等[13]通过考虑双前导车信息的影响，建立了扩展优化速度模型，通过数值仿真分析，研究得出考虑双前车能够更有效抑制交通阻塞。刘有军等[14]通过引进换道系数和换到阈值，对两车道交通流格子模型进行了改进，通过Vissim仿真确定了换道阈值，采用Matlab编程对改进后的两车道交通流格子模型进行了模拟分析。Ahmed等[15]最早提出了基于效用函数的换道需求模型，考虑了前方紧邻的前导车，将换道行为描述为一个概率事件。王昊等在Ahmed等的研究基础上，考虑双前导车引入模型的效用计算，并对原模型进行了适当简化。因此，本研究在王昊等人引入双前导车的跟驰换道模型基础上，建立了高速公路施工路段客货混行的交通流模型场景，确定了小汽车和货车混行状态下的跟驰和换道模型，并采用仿真的方式研究了货车混入率对交通流运行状态的影响。

1 混合交通流模型

1.1 建立交通场景

根据深圳机荷高速升级改造工程施工方案，本研究建立了单向车道施工路段混合交通流模型场景。路段上游包含3条车道，在施工区缩减为两条车道。路段全长1 500 m，分为3个区域：区域1长500 m，车辆在3个车道上行驶，并可执行任意换道；区域2长500 m，车辆同样在3个车道上纵向行驶，并可在内侧车道和中间车道间之间任意换道，外侧车道上的车辆需强制换道至中间车道，如在到达施工区前仍未成功汇入中间车道，需要在施工区前停车等待；区域3长500 m，车辆在内侧车道和中间车道上行驶，禁止换道。

图1 高速公路施工区域的交通场景Fig.1 Traffic scene in expressway construction area

1.2 纵向跟驰模型

全速度差跟驰模型可以很好地体现驾驶员在跟车行驶时，减少与前车直接的速度差和保持与前车之间的适当间距的行驶特点[17]。小汽车在当前时刻的加速度可由速度、速度差和间距计算获得：

(1)

式中，αs为小汽车在当前时刻的加速度；V(Δx)为FVD模型中的优化速度函数；Δx为目标车辆与前车的车头间距；vs为目标车辆速度；Δv为目标车辆与前车之间的速度差；k为驾驶人反应灵敏度系数,λ为速度差项权系数;V(s)为Newell提出的优化速度函数[18]，其表达式如下所示：

(2)

(3)

式中，s为车头距离，也可为Δx；vd为小汽车的期望速度；L为前车的车长；s0为拥堵时的最小车头间距；α为参数。

货车司机的视线比小客车司机的视线高，小客车的跟驰行为受前方一辆车的影响，货车的跟驰行为受到前方两辆车的影响。采用双前导车全速度差模型模拟货车的跟驰行为[16]，其表达式如下所示：

(4)

Δx1=xl1-xs，

(5)

Δv1=vl1-vs，

(6)

Δx2=xl2-xs，

(7)

Δv2=vl2-vs，

(8)

式中，Δx1为目标车辆与前方距离最近的第1辆车之间的车头间距；xl1为目标车辆前方最近第1辆车的位置；xs为目标车辆位置；Δx2为目标车辆与前方距离最近的第2辆之间的车头间距；xl2为目标车辆前方最近第2辆车的位置；同样为优化速度函数，Δv1为目标车辆与前方距离最近的第1车辆之间的速度差，Δv2为目标车辆与前方距离最近的第2辆之间的速度差；vl1为目标车辆前方最近第1辆车的速度；vl2为目标车辆前方最近第2辆车的速度；k1，k2，λ1，λ2为双前导车模型中的参数。

1.3 横向换道模型

高速公路施工路段前后，车辆的换道行为主要分为任意换道和强制换道。任意换道是指，车辆为达到更快的行驶速度和更大的行驶空间而换道进入交通环境更好的车道。强制换道是指，因前方施工区阻挡车道，车辆汇入相邻的可通行的车道。任意换道行为由换道需求和换道条件共同决定。采用车道效用来判断车辆的换道需求。由于货车驾驶员的视线比汽车驾驶员视线高，所以在考虑各车道对于货车的效用时，需要考虑前方紧邻的两辆车对于货车的影响。

1.3.1 货车任意换道模型

(9)

(10)

(11)

Δxdes,vn=V-1(vn)，

(12)

货车产生换道至车道i的需求的概率采用Logit模型进行计算[18]，如式(13)所示：

(13)

货车接受换道条件要基于货车对理想安全间隙的要求[19]。理想安全间隙通过货车的行驶速度、货车与相邻车道上前车的速度差来决定，前方理想间隙和后方理想间隙的具体计算方法如下：

(14)

Δvl=vn-vn-1，

(15)

(16)

Δvf=vn+1-vn,

(17)

驾驶员接受理想间隙的概率满足对数正态分布，货车接受换道条件的概率为：

Pn(e|vn)=Pn(dl,n(t)|vn)Pn(df,n(t)|vn)=

(18)

式中，Pn(e|vn)为速度vn时换道条件接受概率；df,n(t)为目标车辆n在t时刻与相邻车道前车的间距；dl,n(t)为目标车辆n在t时刻与相邻车道上后车的间距；σf，σl为货车可接受的前方和后方换道间隙的对数标准差。

1.3.2 小汽车任意换道模型

除车道效用计算方式外，其他均与货车任意换道模型相同。车道对小汽车的效用如式(19)所示：

(19)

1.3.3 强制换道模型

在区域2，要从外侧车道强行汇入中间车道的车辆，在相邻间隙满足理想换道间隙时进行换道。如式(20)所示：

(20)

2 仿真与分析

2.1 参数设置

采用开放性边界条件，在路段起点以移位负指数分布产生车辆。货车只允许在外侧车道和中间车道行驶。根据机荷高速交通管理情况，及施工区交通组织管理方案，确定起点输入车辆的速度上下限。进入外侧车道的车辆最高速度为100 km/h，最低速度为60 km/h；进入中间车道的车辆的最高速度为100 km/h，最低速度为80 km/h；进入内侧车道的车辆的最高速度为120 km/h，最低速度为90 km/h。在区域1内行驶的车辆最高速度均不超过进入路段时的最高速度限制。从区域2开始进行限速，外侧车道、中间车道和内侧车道的最高速度分别为80、80和100 km/h。仿真时长共1 h，一个时间步长为1 s。车辆从前往后更新其加速度、速度和位置，车辆不允许连续换道。为了减少仿真中的随机误差，每次试验进行10次取其平均值作为试验结果。

根据对深圳机荷高速行驶车辆的统计分析，确定交通仿真车辆类型。交通流中，包含3种车型：小汽车、A类货车和B类货车。其中，A类货车是指车长为8 m的车辆，B类货车是指车超过10 m的车辆。小汽车车长为5 m。因不同车辆的动力性能不同，其加速度有所差异。货车尺寸、重量大，加速时间较长，即货车的重量越大，其加速度越小。小汽车的最大加速度为3 m/s2，A类货车的最大加速度为2 m/s2，B类货车的最大加速度为1 m/s2[20]。根据机荷高速公路监控视频数据标定跟驰模型和换道模型中的模型参数，模型参数取值如表1所示。

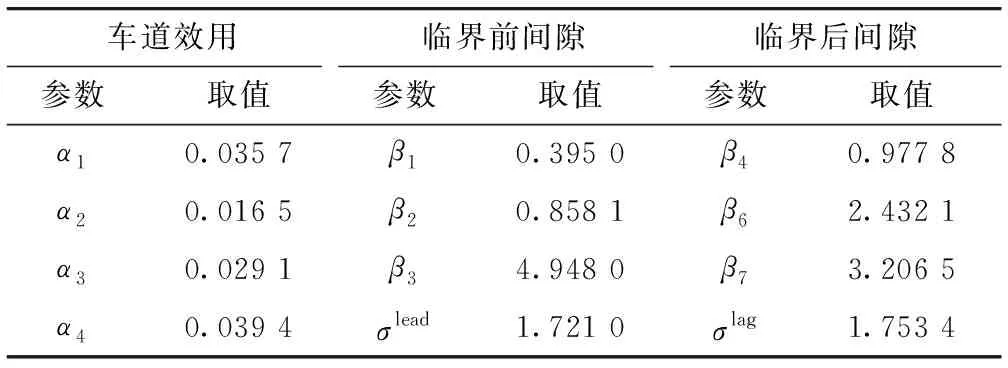
表1 模型参数标定Tab.1 Calibration of model parameters

2.2 交通拥堵

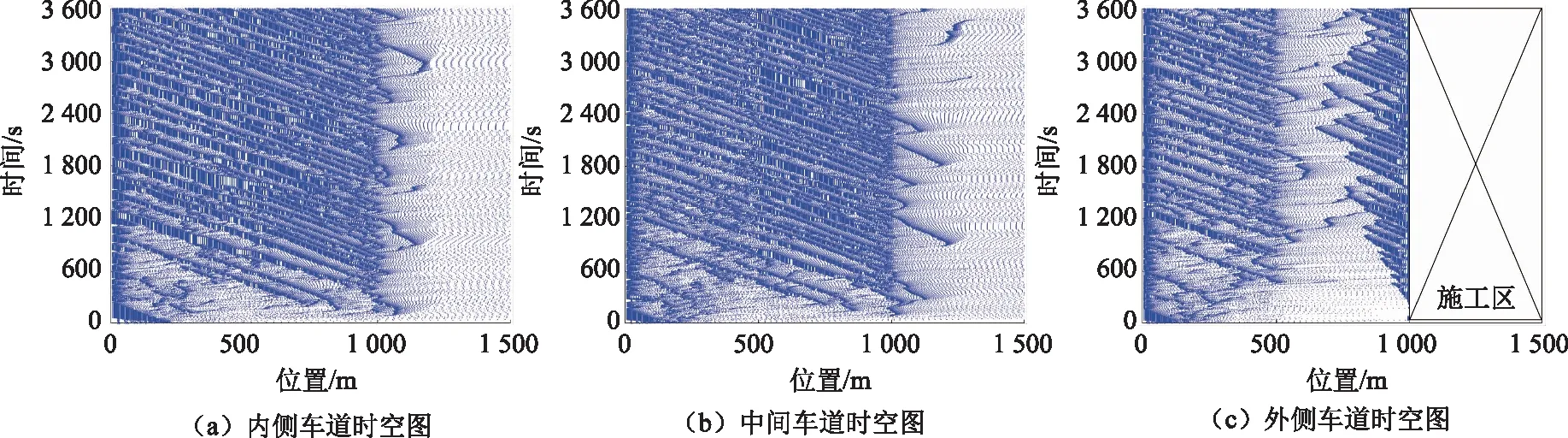
图2 无货车时各车道时空图Fig.2 Spatio-temporal diagrams of each lane without truck

图3 A类货车混入率为25%时各车道时空图Fig.3 Spatio-temporal diagrams of each lane when mixing rate of type A truck is 25%

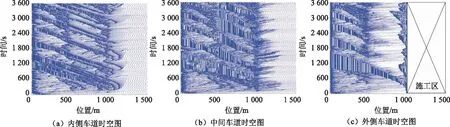
图4 B类货车混入率为25%时各车道时空图Fig.4 Spatio-temporal diagrams of each lane when mixing rate of type B truck is 25%

根据机荷高速实际情况，拥挤流状态下，货车比例最高可达25%。改变货车混入率，分别设置为0%和25%，对施工路段进行仿真。通过3个车道的时空图可见，货车的加入对施工路段的交通拥堵状况影响较大。当没有货车加入时，内侧车道和中间车道在区域3内的交通状况良好，行车流畅。内侧车道和中间车道在区域2内的交通状况略显拥挤，但未产生长时间的排队等待和拥堵。外侧车道的车辆从进入区域2开始便逐渐汇入中间车道，起初区域2内交通状况良好。但随着仿真的进行，外侧车道的车辆不能及时地在区域2内汇入中间车道，以致在区域3前停车等待，使排队长度逐渐增加，导致外侧车道拥堵。当有A类货车混入大道25%时，车辆在3个车道内的行驶均不同程度受到影响，从时空图上可以看出车道占有率有所降低。当B类货车混入率达到25%时，车流运行稳定性受到的影响更大，车辆在区域2内更难以汇入左侧车道，中间车道和外侧车道上都产生了延续时间更长的拥堵交通流。

图5 无货车时各车道时空图Fig.5 Spatio-temporal nephograms of each lane without truck

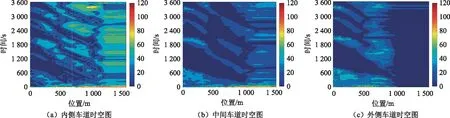
图6 货车混入率为50%时各车道时空图Fig.6 Spatio-temporal nephograms each lane when truck mixing rate is 50%

2.3 行驶速度

货车混入率的改变对车辆行驶速度也有不利影响。在进入区域3之前，车辆的换道行为对交通流产生干扰，使后方车辆减速，限制了区域1和区域2内车辆的行驶速度。区域3内禁止换道，车辆的行驶速度较高。外侧车道因车辆急需汇入中间车道，行驶空间比其他两个车道较为充足，车辆的行驶速度较高。当没有货车时，交通环境虽然较为拥挤，但运行稳定。但当货车混入率增长到50%，内侧车道交通流不稳定，车辆反复加速减速。中间车道和外侧车道上车辆因停车等待，导致上游大量车辆减速停车，且持续时间长。

2.4 通行能力

在1 250 m处设置监测点统计该点的交通流量，取最大的流量作为路段通行能力。统计货车混入率从0增长到50%的路段通行能力。随着货车的增加，路段通行能力逐渐减低，从1 750 veh/h降低到1 500 veh/h。当货车混入率增长到30%之后，通行能力的变化趋于稳定，没有明显下降。货车在施工路段行驶，限制了小汽车的行驶空间，使车辆难以在施工区前及时汇入中间车道，从而影响了路段通行能力。

在Vissim中建立同一交通场景，改变货车混入率，得到不同货车混入率下的路段通行能力。通过Vissim仿真得到的通行能力变化，与Matlab仿真得到的结果一致。进一步证实货车混入率对施工路段通行能力的不利影响。

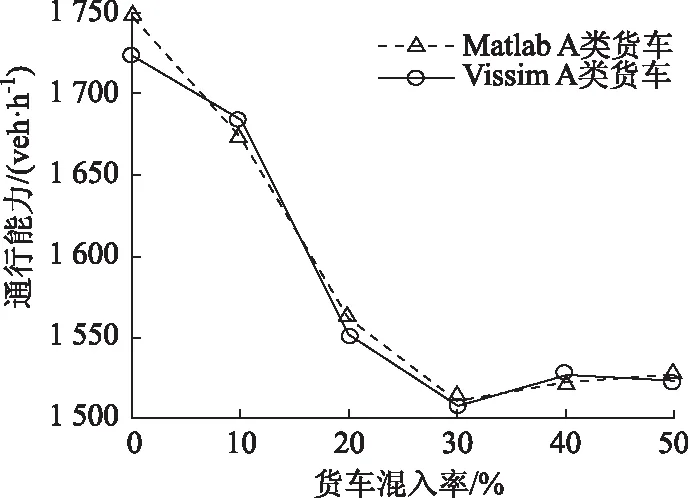
图7 货车混入率对通行能力的影响Fig.7 Influence of truck mixing rate on capacity

3 结论

通过建立高速公路施工路段客货混行交通流，分析货车混入率对交通环境、行驶速度和通行能力的影响。根据货车驾驶员的视线高度的特征，选择双前导车跟驰模型。根据货车长度和启动性能，对机荷高速交通流中货车进行分类。分析不同货车混入率对机荷高速施工路段交通运行的影响。由分析结果可见，货车在施工路段行驶会使车辆不能从外侧车道及时汇入中间车道，从而导致拥堵，降低通行效率，影响行车安全。车身越长、启动性能越差的货车混入率越高，施工路段的排队拥堵状况越严重。

为避免机荷高速在升级改造过程中产生严重拥堵，降低交通效率。应在施工路段上游提前引导大型货车绕行分流，限制大型货车的驶入，从源头避免货车对施工路段交通的不利影响。