刚构桥梁墩梁结合部的拓扑优化及拉压杆模型

余茂峰，杨 屾，李 闯，戴少东，贺志启

(1.浙江数智交院科技股份有限公司，浙江 杭州 310030; 2.东南大学 土木工程学院，江苏 南京 211189)

0 引言

整体长联刚构体系桥梁通过墩梁固结传递荷载(见图1)，具有整体刚度好、行车舒适、后期维护少等诸多优点[1]。目前世界上最长的整体长联高架桥是2017年建成的比利时A11高速公路K032高架桥[2]，该650 m长联由23孔构成，桥墩和主梁之间采用完全刚性连接。在国内，广州地铁12号线、郑州市四环线、浙江杭绍甬高速公路上虞1号高架桥等桥梁采用跨度为30～46 m的多跨长联连续刚构体系，以达到减少支座维护、降低运维成本的预期。

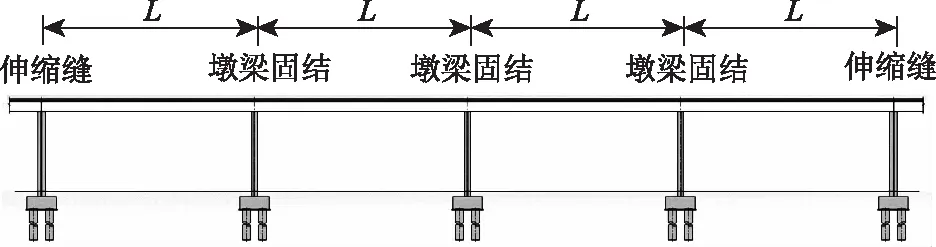
图1 整体长联刚构体系桥梁的基本布置Fig.1 General layout of integral long rigid-frame system bridge

在整体长联刚构体系桥梁中，墩梁结合部是关键的连接构造和受力部位。墩梁结合部可视为T形节点，承受以弯矩为主的弯、剪耦合作用，是典型的应力扰动区[3]。我国2018版《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[4](下称公路桥规)中推荐采用拉压杆模型等方法进行应力扰动区的设计。拉压杆模型是从混凝土结构连续体内抽象出的一种简化力流分析模型，由压杆、拉杆和节点组成，用以反映结构内部的传力路径[5]。针对拉压杆模型合理构形的问题，常用的方法有荷载路径法、应力迹线法、拓扑优化法等[6-7]，但迄今仍没有普适性的简明方法。国内外学者针对建筑框架结构的L形和十字形梁柱节点，开展了基于软化拉压杆模型的节点抗剪承载力计算方法研究[8-11]，以及基于拓扑优化的节点区域拉压杆模型构形研究[12]。美国加州大学Sritharan[13]针对盖梁与桥墩的连接节点，开展了基于拉压杆模型的节点抗震性能评估研究。由于刚构体系墩梁结合部T形节点的受力工况和传力机理复杂，目前尚缺少合适的拉压杆模型构形方法。

本研究基于拓扑优化分析方法，研究了典型工况下墩梁结合部T形节点的弯矩和剪力传递路径，并构建了相应的拉压杆模型，可直接用于结合部的配筋设计。

1 墩梁结合部的内力分析

多跨长联刚构体系桥梁结构承受的主要荷载作用可以分为两类[14]：一是温度、制动力等引起的水平力作用；二是恒载、汽车活载等引起的竖向力作用。为掌握墩梁结合部的内力情况，将多跨长联桥梁结构简化为图2所示的框架结构进行分析。在梁端水平力和跨中竖向力工况下，刚构体系的弯矩分布可以利用力法进行求解。节点区域的弯矩分配取决于主梁与桥墩的线刚度比β：

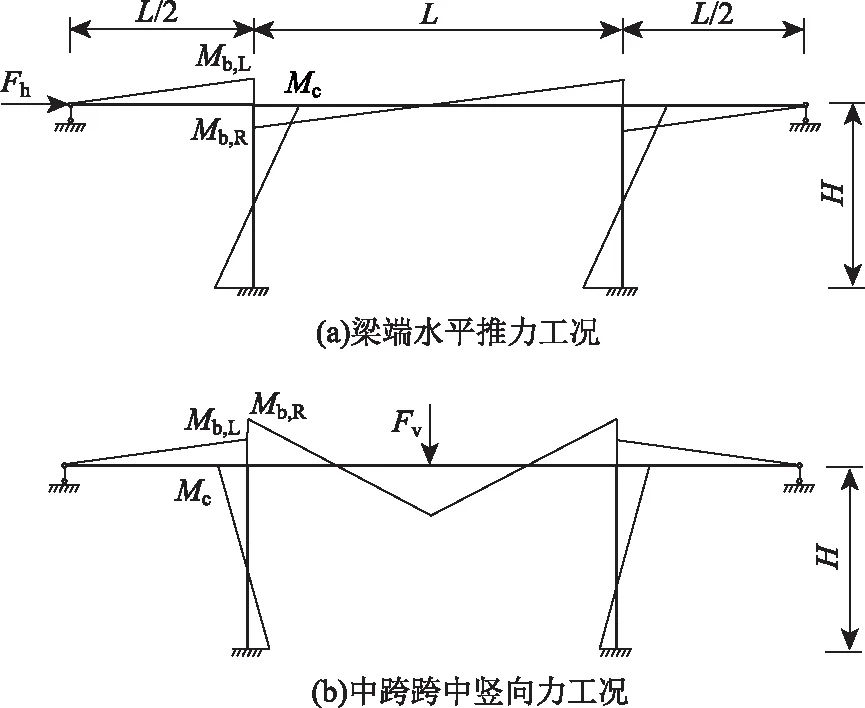
图2 典型工况下刚构体系的弯矩分布Fig.2 Distribution of bending moments in rigid-frame system under typical working conditions

(1)

式中，ib，ic分别为一跨主梁及桥墩的线刚度；Ib，Ic分别为主梁截面惯性矩及桥墩截面顺桥向惯性矩；L，H分别为主梁跨径及桥墩高度；Ec为混凝土弹性模量。

在梁端水平力Fh作用下，墩梁结合部两侧作用的梁端弯矩大小相等、方向相同(这里定义弯矩以逆时针为正)，柱端弯矩值是梁端弯矩值的2倍，可以表达为：

(2)

Mc=-2Mb,L,

(3)

式中，Mb,L，Mb,R分别为节点左侧和右侧梁体的弯矩；Mc为节点的柱端弯矩；弯矩以逆时针为正。

在跨中竖向力Fv作用下，墩梁结合部两侧作用的梁体弯矩方向相反(弯矩以逆时针为正)，可以表达为：

(4)

(5)

(6)

根据式(4)～式(6)，可以定义节点梁体右端与左端所承受弯矩大小的比值α为：

(7)

由此可见：跨中竖向力工况下，墩梁结合部右端梁体弯矩是左端的2倍以上。以浙江杭绍甬高速公路上虞1号高架桥为例，该桥采用7×30 m整体长联刚构体系，主梁为14片30 m标准跨径T梁，桥墩高度为20 m左右，采用双肢薄壁墩。经计算，主梁与桥墩线刚度比β取值约为5，则式(7)中的α取值约为2.3。

墩梁结合部的剪力和轴力等内力情况，亦可通过结构力学方法确定，在此不再赘述。

2 墩梁结合部的拓扑优化分析

2.1 拓扑优化的原理及二次开发

拉压杆模型的自动生成问题可转化为连续体的拓扑优化问题。结构渐进拓扑优化(ESO)的原理[15-16]为：不断地从连续体中剔除应变能密度低的单元，实现结构总体刚度的极大化，即结构应变能的最小化，优化的目标函数为：

Minimize：∑CjWj，

(8)

式中，Cj为结构中单元j的应变能；Wj为单元j的重量。

通过定义结构性能指标PI，则优化目标是使PI取得极大值，即：

(9)

式中，C0,W0分别为初始状态结构的应变能和重量；Ci,Wi分别为经过i次优化后结构的应变能和质量；下标中的“0”表示初始状态；“i”表示经过第i次优化后的状态。

本研究通过对通用有限元程序ANSYS进行二次开发，实现了结构渐进拓扑优化功能，可实现拉压杆模型的自动生成[17-18]。该程序的基本流程为(见图3)：不断地剔除低应变能密度的单元，直至有限元模型的连续性遭到破坏而不能运算为止，性能指标PI取得最大值时对应的拓扑构形即为最优构形。

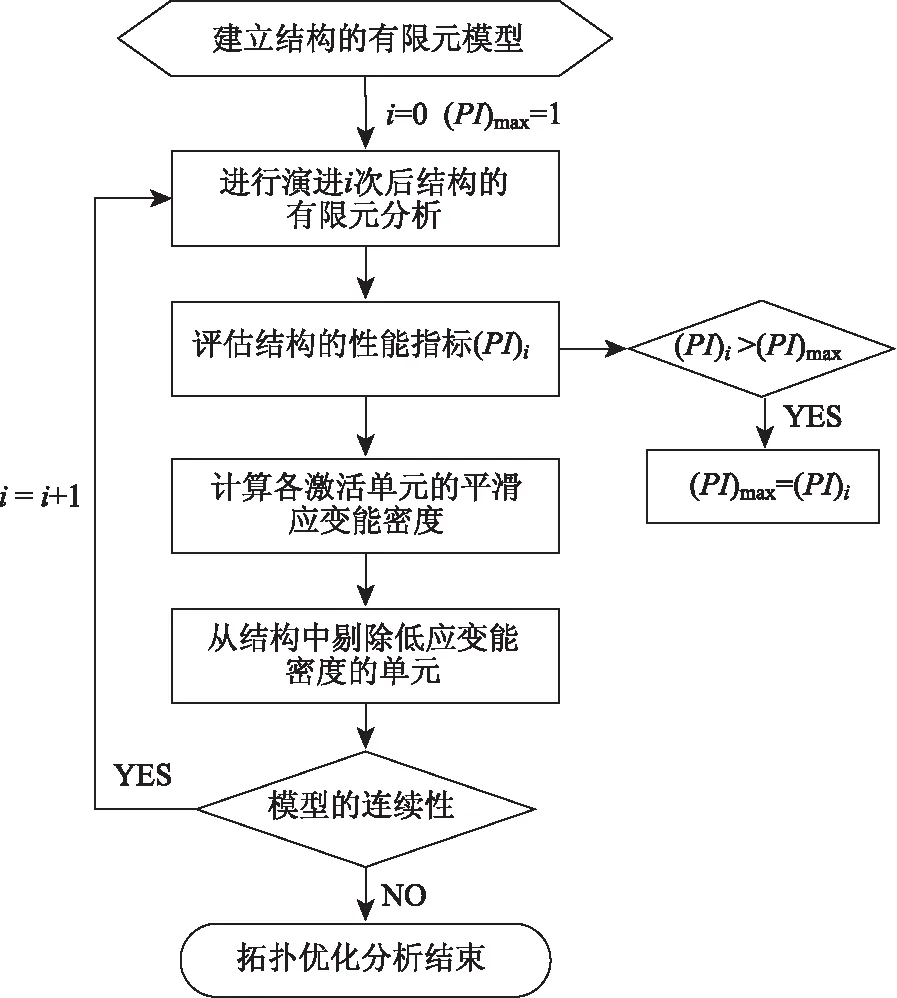
图3 拓扑优化分析的流程Fig.3 Flowchart of topology optimization analysis

2.2 结合部弯矩传递的拓扑优化分析

在水平力工况下，墩梁结合部两侧作用的梁端弯矩大小相等、方向相同，柱端弯矩值是梁端弯矩值的2倍。这里利用本研究编制的程序进行墩梁结合部的拓扑优化分析。图4显示了结合部在此边界力情形下的渐进演化过程。当演进至第60步时，性能指标PI达到最大值1.79，此时对应的最优拓扑构形为X形。在竖向力工况下，墩梁结合部两侧作用的梁端弯矩方向相反，且右端弯矩值是左端的α倍(前述上虞1号高架桥，α取值为2.3)。图5显示了结合部在此边界力情形下的渐进演化过程。当演进至第55步时，性能指标PI达到最大值2.0，此时对应的最优拓扑构形为“△”形。

图4 水平力工况下墩梁结合部弯矩传递的拓扑优化分析Fig.4 Topology optimization analysis of pier-girder joint bending moment transfer under horizontal force working condition

图5 竖向力工况下墩梁结合部弯矩传递的拓扑优化分析Fig.5 Topology optimization analysis of pier-girder joint bending moment transfer under vertical force working condition

2.3 结合部剪力传递的拓扑优化分析

在梁端水平力Fh作用下，结合部左侧梁体的轴力为Fh、右侧梁体的轴力为0.5Fh，则传递至桥墩的水平剪力为0.5Fh。图6给出了结合部在此边界力情形下的渐进演化过程。当演进至第45步时，性能指标PI达到最大值2.1，此时对应的最优拓扑构形为“X”形。

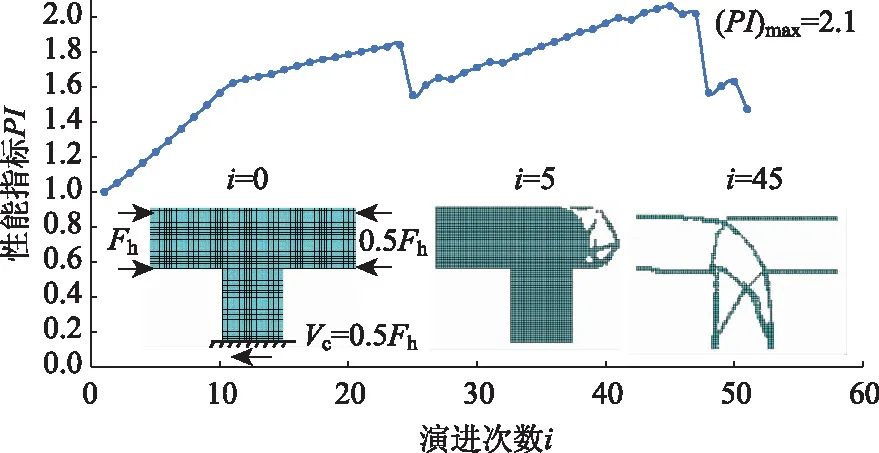
图6 水平力工况下墩梁结合部水平剪力传递的拓扑优化分析Fig.6 Topology optimization analysis of pier-girder joint horizontal shear transfer under horizontal force working condition

在跨中竖向力Fv作用下，结合部右端的竖向剪力为Vb,R= 0.5Fv，左端的竖向剪力vb,L为：

(10)

式中λ为剪力比例系数。

以浙江杭绍甬高速公路上虞1号高架桥为例，主梁与桥墩的线刚度比β约为5，则Vb,L= 0.085Fv。图7给出了结合部在此边界力情形下的渐进演化过程。当演进至第42步时，性能指标PI达到最大值1.33，此时对应的最优拓扑构形为鱼腹形。

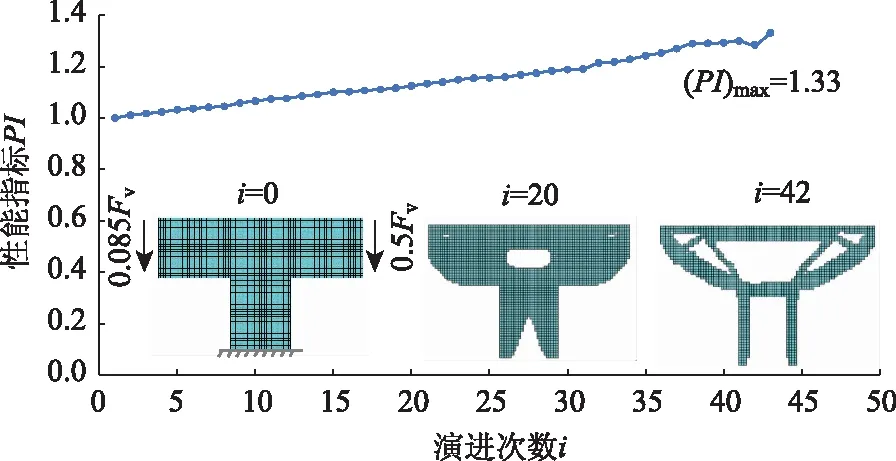
图7 竖向力工况下墩梁结合部竖向剪力传递的拓扑优化分析Fig.7 Topology optimization analysis of pier-girder joint vertical shear transfer under vertical force working condition

3 墩梁结合部的拉压杆模型

3.1 4种典型工况下的拉压杆模型

拓扑优化分析的结果可以作为拉压杆模型构形的直接依据[15]。表1给出了4种典型工况下墩梁结合部的拉压杆模型及拉杆内力计算公式，再结合公路桥规中对拉杆承载力的计算规定[4]，可直接用于结合部的配筋设计。参考公路桥规的规定，拉压杆模型的内力臂z可取为0.9h0(h0为梁体或墩柱截面的有效高度)。

表1 典型工况下墩梁结合部的拉压杆模型及拉杆内力计算公式Tab.1 Strut-and-tie models for pier-girder joints and calculation formula of internal force of tie under typical working conditions

根据表1中的拉压杆模型，可以清晰地得出墩梁结合部的传力路径及关键受力效应：

(1)在水平力工况下，结合部通过“X”形交叉的斜拉杆和斜压杆传递两侧梁部的同向弯矩，一侧梁顶至另一侧梁底的连续配筋是传力的关键构造。

(2)在竖向力工况下，结合部通过“△”形交叉的斜拉杆和斜压杆传递两侧梁部的反向弯矩，将桥墩受拉侧钢筋内弯伸入结合部顶部是传力的关键构造。

(3)在水平力工况下，水平剪力通过交叉桁架传递至桥墩，将桥墩受拉侧钢筋竖直伸入结合部是传力的关键构造。

(4)在竖向力工况下，竖向剪力通过斜压杆进行传递，将梁顶的钢筋下弯，对控制斜向受剪裂缝的开展有利。

我国新版《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[4]中给出了拉压杆模型构形的基本准则和方法，包括拓扑优化法、应力迹线法、力流线法等。但是，针对墩顶结合部这一具体构造和受力情形，规范中并没有给出具体的拉压杆模型构形。本研究遵循了规范中建议的拓扑优化分析方法，给出了墩梁结合部的拉压杆模型，是对规范的有益补充。

利用表1计算得到拉杆内力后，可根据公路桥规按下式进行相应的配筋计算：

fsdAst+fpdAps≥γ0Td,

(11)

式中，γ0为桥梁结构重要性系数；Td为拉杆内力设计值；fsd为普通钢筋抗拉强度设计值；Ast为充当拉杆的普通钢筋面积；fpd为预应力钢筋抗拉强度设计值；Aps为充当拉杆的预应力钢筋面积。

3.2 复合受力下的拉压杆模型

墩梁结合部往往受到弯矩、剪力和轴力的复合作用，受力十分复杂。基于前述的单工况分析结果，图8给出了复合受力情形下的拉压杆模型构形示意图，可供设计参考。根据Schlaich等[5]的建议，也可偏于简化和保守考虑，按各单个工况分别进行配筋设计并叠加。

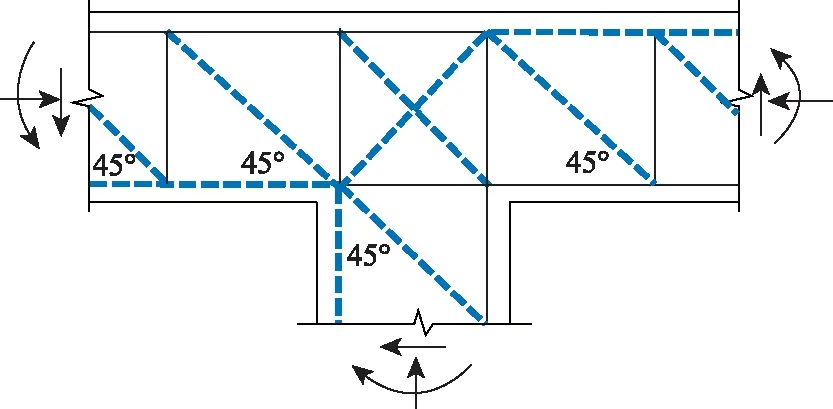
图8 弯矩剪力轴力共同作用情形下的拉压杆模型Fig.8 Strut-and-tie model under combined action of bending moment, shear force and axial force

4 结论

本研究基于拓扑优化方法和拉压杆模型方法，研究了典型工况下墩梁结合部T形节点的弯矩和剪力传递路径，主要结论有：

(1)基于结构渐进拓扑优化分析，可以清晰地得到墩梁结合部T形节点在典型工况下的最优拓扑构形和传力路径。

(2)在水平力工况下，结合部通过X形交叉的拉杆和压杆传递梁部两侧的同向弯矩，通过交叉桁架传递水平剪力；在竖向力工况下，结合部通过Δ形交叉的拉杆和压杆传递梁部两侧的反向弯矩，通过斜压杆传递竖向剪力。

(3)构建了4种典型受力情形下墩梁结合部的拉压杆模型，并给出了拉杆内力计算公式，可供配筋设计参考。

(4)本研究将墩梁结合部看作平面问题进行分析，有一定的近似性。实际上，上部结构往往由多片梁构成，上部结构荷载通过墩梁结合部传递至盖梁再传递至桥墩，具有一定的空间传力特征，值得进一步研究。