基于k 近邻的多尺度超球卷积神经网络学习
刘子巍,骆 曦,李 克,陈富强
(北京联合大学智慧城市学院,北京 100101)
0 概述
随着深度学习技术的快速发展,其在人脸识别、机器翻译、自然语言理解、业务管理等领域得到了广泛的应用[1-3]。以卷积神经网 络(Convolutional Neural Network,CNN)为代表的深度学习模型主要面向图像[4-5]、视频[6]、语音[7]等数据类型,数据样本的基本特征是均匀致密采样、各属性项性质相同的欧氏域数据,此处称之为均匀同质欧氏数据。
卷积神经网络在图像识别等领域得到有效应用,其中一个重要原因在于其能从输入数据中学习出数据的空间结构特征,即如果一个输入变量与其相邻的输入变量之间的关系比与距其较远的输入变量之间的关系更密切,则可认为这样的数据具有空间结构特征。例如在图像识别中,构成图像某个局部要素(如眼睛)的临近像素点之间的相关性比间隔较远的像素之间相关性更大。因此,可以借助CNN卷积窗的迭代训练来提取这种特征。
除了上述数据之外,在实际应用中还有一大类数据并不具备上述特征,如气象监测数据、用户购物记录以及各类工业企业经营过程中大量产生并留存的业务数据。这类数据通常以二维表的形式存储,表头为各样本的属性项,通常称之为结构化数据。此类数据各属性项的含义、数据类型、取值范围通常有很大区别,具有异质特性,且各样本是在整个高维属性空间中通过非均匀、稀疏采样获得的,但在多数应用中仍可以用欧氏距离来描述样本间的相似性特征,此处称之为非均匀异质欧氏空间数据。在深度学习兴起之前,对这类数据的分析预测通常采用以k近邻(k-Nearest Neighbor,kNN)、决策树、支持向量机(Support Vector Machine,SVM)等为代表的传统机器学习算法。
由于深度学习具有上述优良性质和性能,探索如何将深度学习技术应用于非均匀异质欧氏空间数据和相关场景中的任务是一个具有挑战性且有意义的问题,有助于扩展深度学习的应用领域。目前,已有研究者开展了这方面的尝试,提出了雷达图[8-9]、应用不规则卷积核或可变性卷积核[10-12]、将分类不平衡的数据应用在卷积神经网络[13-15]等方法。
面向异质、非均匀稀疏采样结构化数据集的预测任务,本文提出一种基于k 近邻的超球卷积神经网络学习方法。给出一个朴素的假设,即2 个样本在属性空间中的距离与其标记的相似性高度相关。在此基础上,利用kNN 算法预处理实现异质数据的同质化改造以及邻域样本标记的空间分布特征构造,同时设计多尺度的超球卷积核,从而有效提取目标样本的邻域标记空间分布特征。
1 相关工作
1.1 非均匀异质欧氏空间数据
在各个领域中,最常见的数据是图片、视频等均匀采样的欧氏空间数据。在均匀欧氏空间数据集中,样本间可以通过一组相同维度属性,由欧氏距离表示样本间和样本内各采样点间的相似性,样本各个维度的属性具有同质特性。在非均匀欧氏空间数据集中,同样是根据样本间一组相同维度属性构成的欧氏距离表示样本间的相关性,但样本内部属性与属性之间却通常是异质的。
由图1 可以看出,在属性空间中,可以用欧氏距离来衡量样本间的相似性,但样本的空间分布为稀疏、非均匀采样的,这样的数据集通常不能满足kNN 算法所要求的密采样假设。图2 所示的图像是典型的均匀欧氏空间数据,样本中各像素采样点之间具有等距、致密的空间结构特征,更便于利用卷积操作和神经网络迭代提取局部特征。
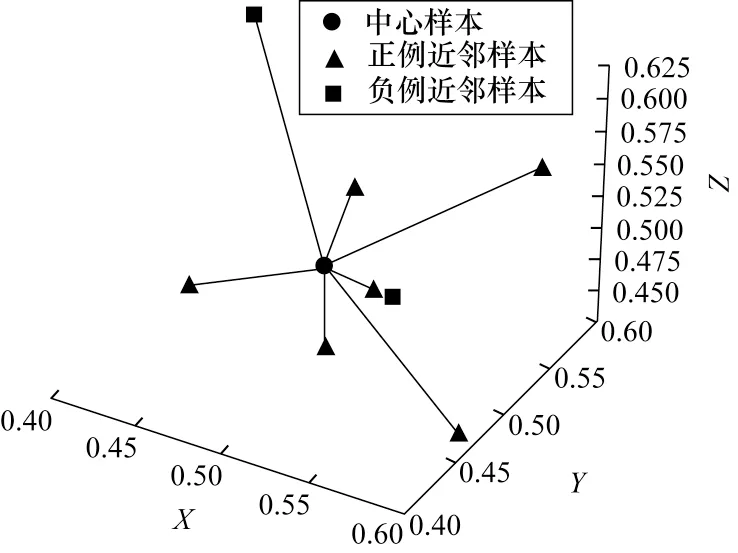
图1 非均匀欧氏空间数据特性Fig.1 Characteristics of non-uniform Euclidean domain data

图2 均匀欧氏空间数据示例Fig.2 Example of uniform Euclidean domain data
1.2 面向异质非均匀欧氏空间数据的深度学习方法
对于非均匀异质欧氏空间数据,多采用传统的机器学习方法进行处理。基于局部不变性先验和密采样假设的kNN 算法对多数数据集简单有效。为了将kNN 扩展到可处理多标记问题,文献[16]提出了ML-kNN 算法。与kNN 核心思想一致,该算法也是通过寻找一定数量的相似样本来判断测试样本标记,但与kNN 不同的是,ML-kNN 通过最大化后验概率的方式推理待测样本的标记项,在处理二分类问题时取得了不错的效果。然而,kNN 算法在复杂分类边界情况下对于边界附近标记高度混淆样本的分类能力较差,尤其对高度不平衡数据,因为其简单的邻域投票机制无法捕捉稀疏正例样本的邻域空间分布特征,而由文献[17]提出的SVM 算法在解决线性可分的二分类问题时获得了较好的效果。
深度学习在均匀欧氏空间数据集的应用中相对于传统机器学习具有明显优势。卷积神经网络由于其特有的平移不变性,在图像识别、语义分割等领域得到广泛应用。文献[18]提出的GoogLeNet 摒弃了传统单纯依靠层数堆积来增加模型深度的方法,而是利用inception 模块在增加模型深度与宽度的同时尽可能减少计算量。在此之后,文献[19]提出的inception-v4 架构将GoogLeNet 中 的inception-v1 架构与残差连接结合,进一步提升了inception 架构的稳定性。
鉴于以CNN 为代表的深度学习在同质均匀采样数据上的优异表现,研究者也围绕如何将这类方法应用于异质数据集展开了研究,这其中最直接的思路是先将异质属性数据进行同质化改造,以适应深度神经网络各层的处理。对此,一种方法是先利用全连接操作将异质属性值转化为同质化的神经元输入,再对神经元进行卷积池化等操作,最后利用Softmax 分类器进行分类预测[20],称之为全连接CNN(Fully Connected CNN,FC-CNN)。FC-CNN 适用领域较广,并且能够得到较好的分类预测效果。文献[8]提出一种基于雷达图表示数值型数据的卷积神经网络分类方法,利用CNN 在图像数据处理领域的优势,先对数值型数据样本进行标准化操作,再将标准化后的N维属性映射到N边形雷达图中,实现异质结构数据向同质结构数据的转化,最后将雷达图数据作为图像数据输入到常规的CNN 模型中进行分类预测。该方法在化工过程数据集中取得了较好的故障分类结果。文献[4]利用CNN 算法进行心脏病预测,先通过词嵌入方法将非结构化数据转换成向量,再输入CNN 模型中进行训练和预测,取得了较好的效果。
1.3 卷积核的设计
在CNN 模型中,卷积核的设计和网络模型的构造是影响分类预测效果的关键部分,其中卷积核的设计尤为重要。为了完成特定的学习任务,可以采用不同的卷积核以及卷积方式来提取感受野的数据特征。以图像识别为例,卷积层的卷积核具有良好的平移不变性,即卷积核仅对特定的特征才会有较大激活值。无论上层特征图中的某一特征平移到何处,卷积核都会在该特征处呈现较大的激活值,目前最常用的方法是矩形卷积窗。为了在扩大感受野的同时减少参数降低计算量,文献[21]提出了空洞卷积,使深层的卷积神经网络在扩大感受野的同时减少了参数数量,以这一方法代替传统增加感受野进行降采样而导致丢失分辨率的方法。文献[22]提出转置卷积这一概念,通过转置卷积使网络模型最优化地进行上采样,并且还可用于可视化卷积的过程。该方法在GAN 等领域中得到大量应用。
卷积神经网络对于输入信息有严格要求,多是规则的矩形排列。文献[10]提出不规则卷积神经网络,将形状与参数与卷积核参数融合,一同在反向传播的过程中更新参数,以此更好地提取贴合待测目标形状的特征信息。该方法在语义分割数据集上获得了较好的效果。
在面向异质非均匀数据的分类预测任务中采用卷积神经网络方法时,一个重要的问题是如何合理设计卷积核以有效提取样本在高维属性空间中邻域样本标记的空间分布特征,本文将对此进行研究。
2 邻域标记特征的提取
异质非均匀数据中各个属性往往具有不同的衡量标准,为了消除各个指标之间的量纲影响,需要先进行数据标准化解决数据指标之间的可比性问题。本文利用min-max 标准化方法对所有属性维度进行归一化处理,如式(1)所示:

其中:x*为标准化后的属性值;x为原属性值;xmin和xmax分别为该属性的最小值和最大值。通过归一化过程,可确保后续邻域标记特征提取与邻域标记样本集构建的准确性。
邻域标记项特征提取的核心思想是利用kNN 的近邻搜索寻找邻域样本标记,即对待测样本在训练集特征空间中根据欧氏距离寻找一定数量的邻域样本,构成邻域样本集,其中,待测样本的标记取为邻域样本集中占比最大的标记值。kNN 算法简单有效,在处理很多分类问题上性能优异,且对噪声不敏感,但是kNN 算法在一些特定条件下效果并不好,如在邻域数据集标记项分布较均衡时预测效果就很不理想。为了定量描述近邻样本标记的混淆程度,定义混淆系数为:

其中:n为待测样本的同标记近邻数;k为总近邻数;Cf∈[ 0,1] 。当近邻中正负例样本数相同时,Cf=0,表示完全混淆;当近邻全部为正例或负例时,Cf=1,表示无混淆。以北京市空气质量监测采样数据集[16]为例,采用kNN 算法进行预测(取k=15),kNN 对于同标记数相同近邻数不同的待测样本的预测准确率如图3所示。可以看出,当混淆系数小于0.3 时,kNN 预测性能明显变差,将此类样本定义为重度混淆样本,对于这类样本,很难利用kNN 实现准确预测。类似地,将混淆系数在0.3~0.6 之间的样本定义为中度混淆样本,而将混淆系数大于0.6的定义为轻度混淆样本,对于轻度混淆样本,可以利用kNN 实现准确预测。
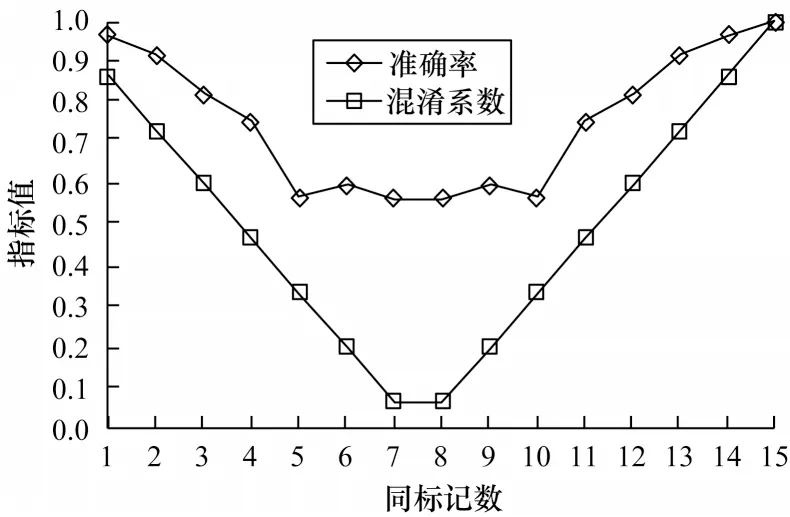
图3 不同近邻混淆条件下的kNN 性能差异Fig.3 Performance difference of kNN under different neighbor confusion conditions
然而,kNN 仅利用了邻域样本标记的统计特征而忽略了其空间结构特征。因此,本文利用邻域样本标记项构成的邻域标记样本集所包含的空间结构信息,并且将数据集的属性描述由异质转变为同质,从而更好地利用CNN 在处理数据的空间平移不变性特征上的优势。首先定义邻域标记样本如下:
定义1邻域标记样本
已知d维样本集D={(xi,yi)|1 ≤i≤m},yi∈Y={1,-1},设Dik={(xik,yik,dik)| 1 ≤k≤K}为中心样本xi在属性空间中前k个邻域样本的属性、标记及其到该中心样本的距离信息集合,各样本按距离排序即dik≤dil(1 ≤k<l≤K)。定义K维邻域标记样本集D*={(xi,yi|1≤i≤m},其中邻域标记样本为Xi=(yi1,yi2,…,yiK),dik≤dil(1≤k<l≤K)。
本文将邻域标记样本集所包含的丰富的标记空间结构特征信息输入卷积神经网络模型进行分类预测,利用邻域标记样本集增加后续卷积操作的特征输入信息。图4 为邻域标记样本集D*示例,其中第1 列为中心样本的标记yi,第2 列为距中心样本最近的邻域样本的标记yi1(1 ≤i≤m),第2列至最后一列根据欧氏距离升序排列,依次类推,颜色越深表示距中心样本越近。
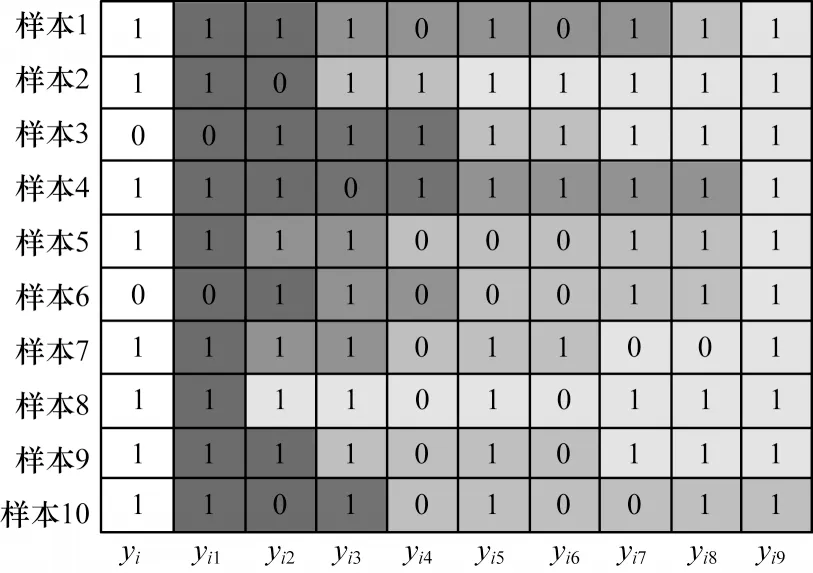
图4 邻域标记样本集示例Fig.4 Example of neighborhood label sample set
由于邻域样本对待测样本的影响通常随距离增大而减小,为了尽可能捕捉不同感受野范围内的邻域标记空间分布特征,本文对邻域标记样本集进行划分,使用不同尺度的邻域标记样本数作为CNN 模型的训练输入样本,在弥补kNN 对单一k值选择局限性的同时,增加CNN 模型输入样本规模和鲁棒性。图5 为邻域标记样本的邻域尺度示例(彩色效果见《计算机工程》官网HTML 版)。可以看出,在原始高维属性空间中,所有邻域样本根据与中心样本间的欧氏距离进行排列并且分布在中心样本附近,图中给出了2 个不同邻域尺度(4 和9)下邻域样本在原始属性空间的分布和标记值,分别对应图中的黑色和蓝色球形区域。依此类推,可以提取更多尺度的邻域样本信息,构造出对应的邻域标记样本集作为CNN 模型的输入数据。
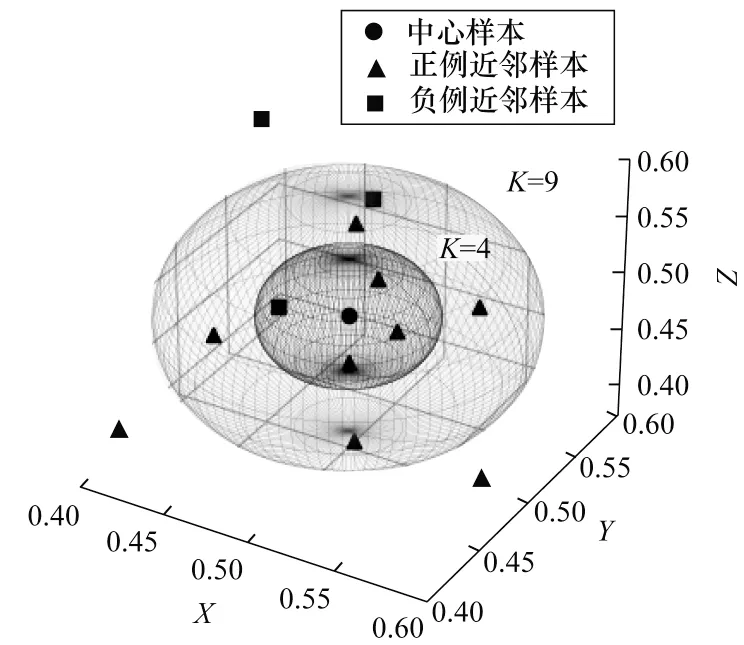
图5 邻域标记样本的邻域尺度Fig.5 Neighborhood scale of neighborhood label samples
3 基于k 近邻的超球卷积神经网络学习
3.1 超球卷积
给出超球卷积定义如下:
定义2超球卷积
对于样本集D及其邻域标记样本集D*∈RK,定义一个尺度为k(1 <k≤K) 的1D 卷积核W(k)=作为对样本特征空间中各中心样本xi的一个超球卷积,即:

超球卷积是在d维特征空间中对中心样本xi的k个邻域样本的标记值进行的卷积操作,具有模型简单、计算量小的优势,具体实现上可通过简单的1D 卷积实现,但与常规的1D 卷积具有不同的物理意义:超球卷积是在原始高维属性空间中提取待测样本与其邻域样本在标记上的统计特征与空间结构特征,其前提是必须先利用kNN 近邻搜索构造出邻域标记样本集作为CNN的输入数据,而不是直接对原始样本进行卷积,其通过选取不同的尺度值k进行卷积,实现对不同范围内邻域样本的标记与空间特征的提取。
超球卷积在原始数据样本的特征空间中采用CNN 而不是利用贝叶斯原理从概率的角度去估计中心(未知)样本的类标记,其通过卷积核的迭代训练来提取局部特征,从而利用CNN 卷积的平移不变性来提取中心样本与邻域样本标记值的相关性特征。超球卷积中的平移不变性提取与CNN 图像识别的处理不同,超球卷积是对整个属性空间进行局部采样构成邻域标记样本集,通过对每个邻域标记样本利用多个尺度卷积核进行一次性的多副本卷积,实现在整个属性空间中的特征提取。
3.2 HCNN 网络模型设计
基于传统CNN 模型,本文引入超球卷积设计超球卷积神经网络(Hypersphere CNN,HCNN)模型。HCNN 将多种不同尺度的邻域标记样本集作为输入,对每条样本的邻域按升序排列并分别提取距中心样本最近的前22,32,…,n2个邻域标记样本构成n-1 种尺度的输入数据。图6 为提取4 种尺度(即k=4,9,16,25)邻域标记样本的示意图(彩色效果见《计算机工程》官网HTML 版)。

图6 多尺度邻域标记样本提取Fig.6 Extraction of multi-scale neighborhood label samples
1)超球卷积层。超球卷积层用于提取各种不同尺度的邻域标记的空间特征,可以用1D 全连接来实现,操作流程如图7 所示,图中采用了4 种尺度,每种尺度均按照式(3)进行400 个副本的超球卷积,形成(n-1)×400 的输出矩阵,并将其转变为每层尺寸为(20,20)深度为n-1 层的张量。
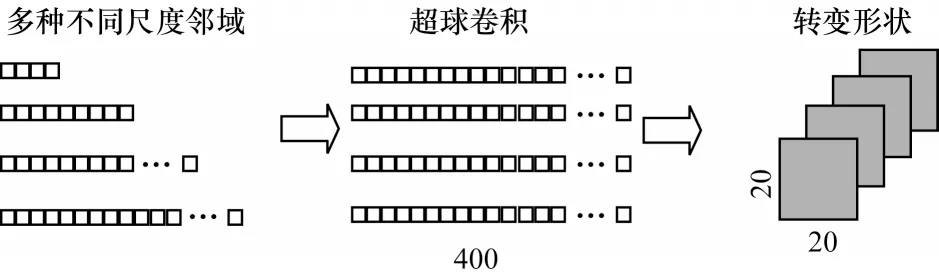
图7 超球卷积层操作流程Fig.7 Operation procedure of hypersphere convolution layer
2)卷积层。由于各层张量代表不同尺度的邻域标记样本,为了使各种尺度提取的特征具有不同的意义以及权重,卷积方式采用深度可分离卷积。深度可分离卷积层与传统卷积层不同之处在于一个卷积核只提取一个通道(层)的特征提取,将各个尺度的邻域分别进行超球卷积以此来对各种尺度的邻域标记进行特征提取。卷积层由依次利用3×3、3×3 和5×5 的卷积核且步长均为1 的3 个深度可分离卷积层所构成,3 次深度可分离卷积具体操作如图8 所示,在每层深度可分离卷积后加入一层Batch Normalization 来加快学习收敛速度,同时避免梯度消失。
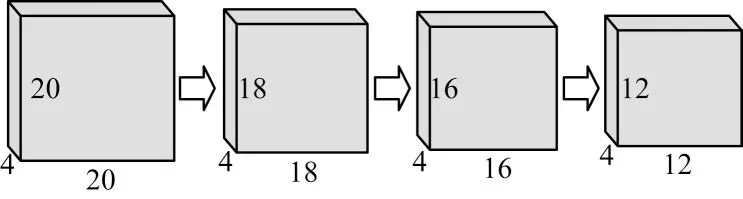
图8 3 次深度可分离卷积Fig.8 Cubic depth separable convolution
3)全连接层。全连接层的目的是利用提取出的特征进行有效分类。该层由普通的多层普通神经网络组成,激活函数采用SELU 函数,并且利用Dropout防止过拟合现象。
4)输出层。输出层利用全连接层实现,用于输出模型判断出的该样本的正例概率,激活函数采用Sigmoid 函数。
5)损失函数。损失函数用于衡量预测值和真实值之间的差距,并用于更新全连接层和卷积层参数,由于本文是针对二分类问题,因此采用二元交叉熵作为损失函数。
以4、9、16、25 这4 种尺度为例,HCNN 模型整体架构如图9 所示。

图9 HCNN 模型整体架构Fig.9 Overall architecture of HCNN model
3.3 HCNN 算法描述
HCNN 模型中主要分为三步:构建邻域标记样本集,HCNN 模型训练和利用HCNN 模型进行分类预测。具体算法描述如下:
算法1HCNN


4 实验结果与分析
4.1 实验数据集
本文实验所使用的数据为北京市昌平气象监测站2013 年3 月1 日—2017 年2 月28 日每小 时的空气污染物监测采样数据[23]。数据集总共包含32 681 条样本,数据样例如表1 所示。数据样本属性包括年、月、日、时、SO2浓度、NO2浓度、CO 浓度、O3浓度、温度、压强、露点温度、降水量和风速。
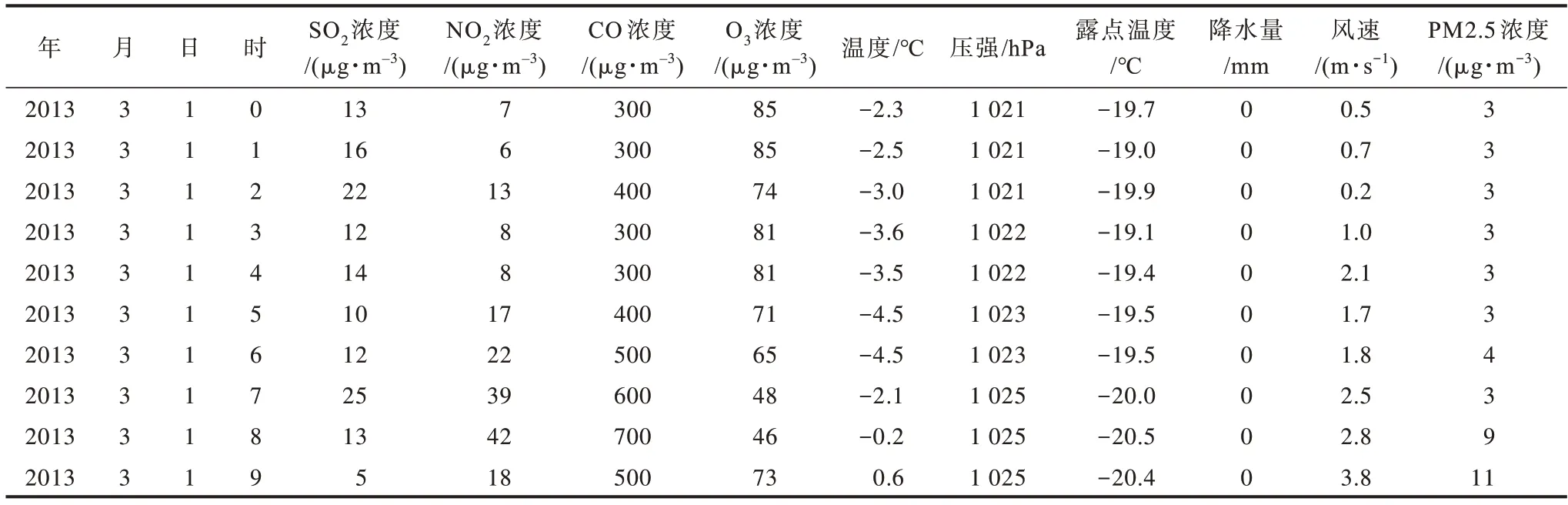
表1 北京市空气污染物监测数据样例Table 1 Samples of air pollutant monitoring data in Beijing
取PM2.5 浓度为标记项。图10 为PM2.5 的概率密度分布,可见出现PM2.5 浓度小于200 的出现天数占绝大部分,因此,将PM2.5 浓度大于200(对应中重度污染)设为正例,共2 116 条样本,在数据集中占6.47%,属于典型的不平衡数据集。作为对照实验,同时取门限50 μg/m3(设PM2.5 浓度小于50 为正例)得到一套平衡数据集,其中正例共17 221 条样本(占比52.69%)。
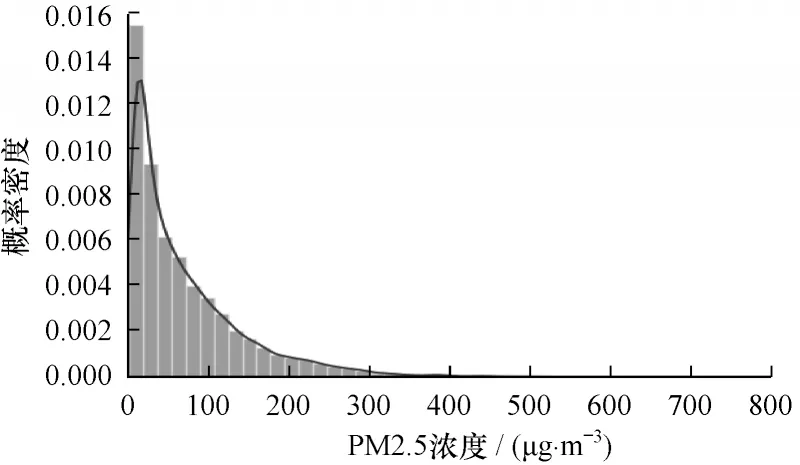
图10 PM2.5 浓度的概率密度分布Fig.10 Probability density distribution of PM2.5 concentration
图11 为各属性与标记项之间相关系数的统计分布,可见SO2、NO2、CO 浓度这三个属性与标记项之间以及这三个属性间均有较高的相关性。
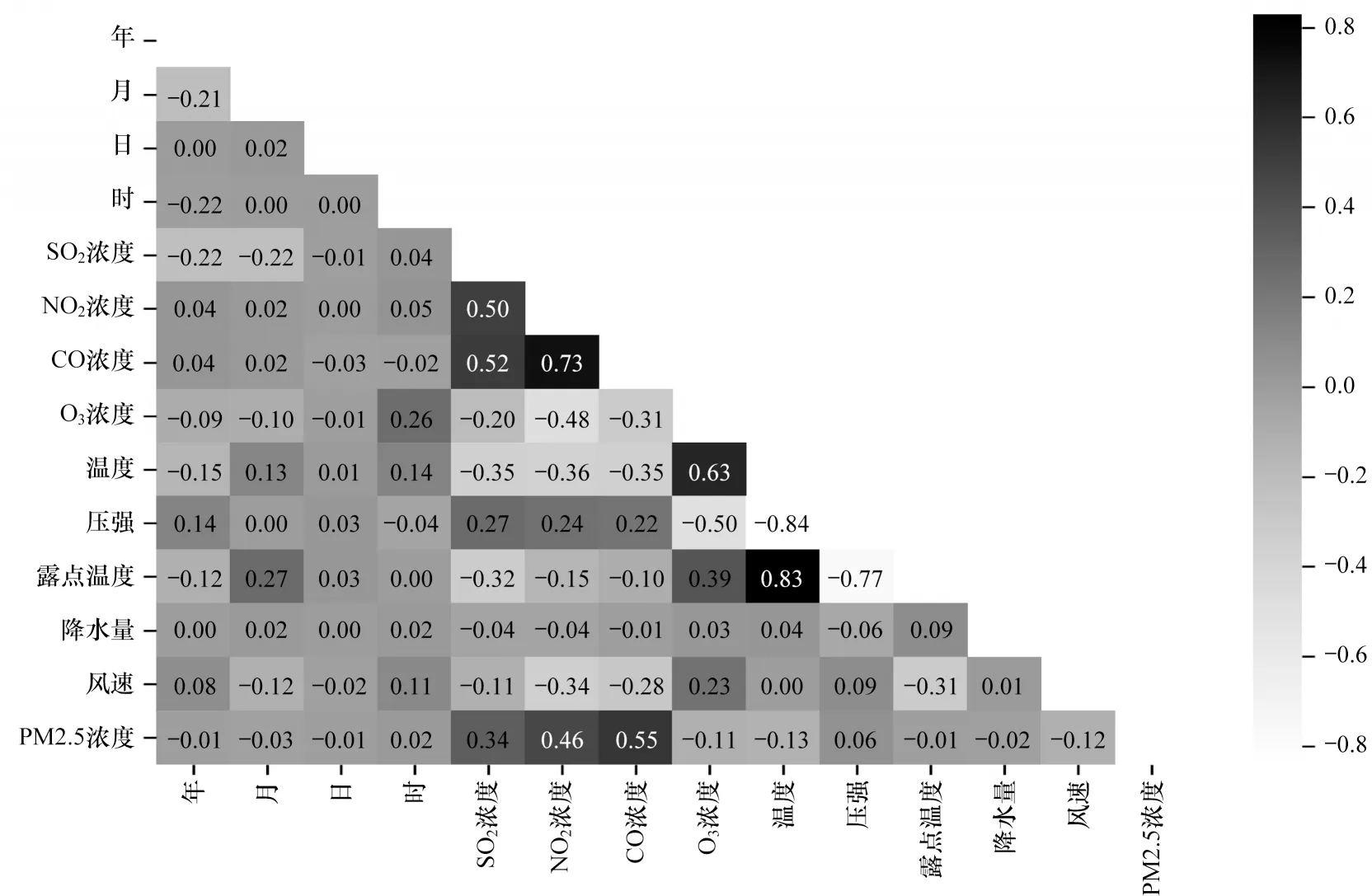
图11 属性及标记项间的相关系数统计分布Fig.11 Statistical distribution of correlation coefficients among attributes and label items
4.2 性能评价准则
由于本文研究的问题属于分类问题,因此评价指标采用准确率、精度、召回率和F1 测度。以下实验均使用Python 语言在PyCharm 平台上完成。
4.3 算法实验分析
本文将HCNN算法与kNN、FC-CNN,Radar-CNN等算法进行对比,并对算法各关键参数的选取进行实验对比。此外,为了对比HCNN 在不采用kNN 预处理时的性能变化,采用普通CNN 模型进行消融实验,其神经网络网络模型与HCNN 基本相同,区别在于对原始的异质数据不经过异质化,而是直接进行卷积处理,下文中称为CNN 算法。将训练集与测试集比例设定为8∶2,采用5折交叉验证的方法得到最终的性能评价结果。
4.3.1 HCNN 实验结果
HCNN模型的训练过程以及收敛曲线如图12所示,其中,图12(a)和图12(b)为训练集的残差与准确率收敛曲线,可见训练集loss 值和准确率在迭代50 次左右时即快速收敛,图12(c)和图12(d)为验证集的残差与准确率收敛曲线,同样在迭代50 次左右逐渐收敛趋于平滑。由此可见HCNN 模型并没有产生明显的过拟合现象,可有效地对未知样本进行预测。
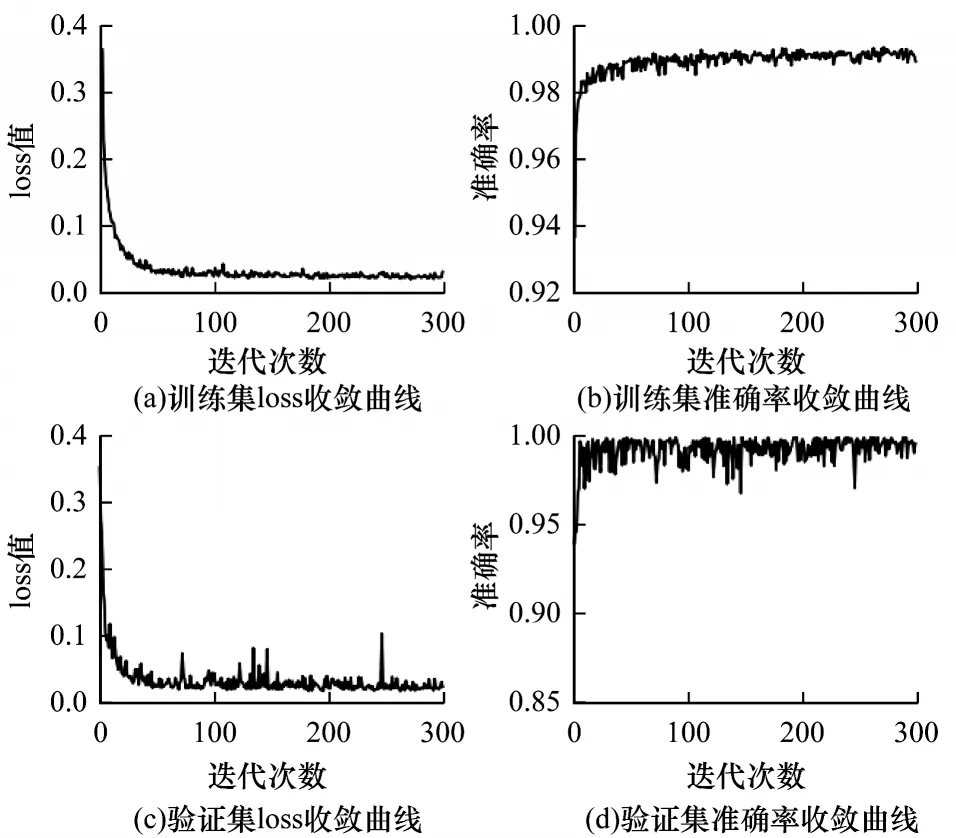
图12 HCNN 模型训练的残差与准确率收敛曲线Fig.12 Convergence curve of loss and accuracy of HCNN model training
4.3.2 超球卷积核最大尺度的选取
邻域样本与中心样本的距离关系如图13 所示(彩色效果见《计算机工程》官网HTML 版),其中,图13(a)是从全部训练数据集中随机抽取200 个样本(不同颜色的曲线代表不同样本与其邻域样本间的欧式距离曲线),取最大邻域尺度为200,分别计算各样本与其邻域样本的欧氏距离并按升序排列绘制的曲线。可以明显看出,当邻域尺度k取到25 以后,中心样本与邻域样本的距离差逐渐趋于平缓。为了评估训练样本规模的影响,从训练集中随机抽取5 000 个样本作为新的训练集进行近邻搜索,结果如图13(b)所示。可以看出,在减小训练集规模后,中心样本与邻域样本间的距离依旧在尺度为25 左右开始趋于平缓。因此,本文实验中取最大尺度数为25。选取更大范围的邻域样本参与训练不仅会导致计算量过大,而且可能因为领域样本的区分度降低而引入不必要的干扰。对于不同的应用数据集,仍建议将最大尺度数作为一个重要的超参数,通过上述分析找到最优值。
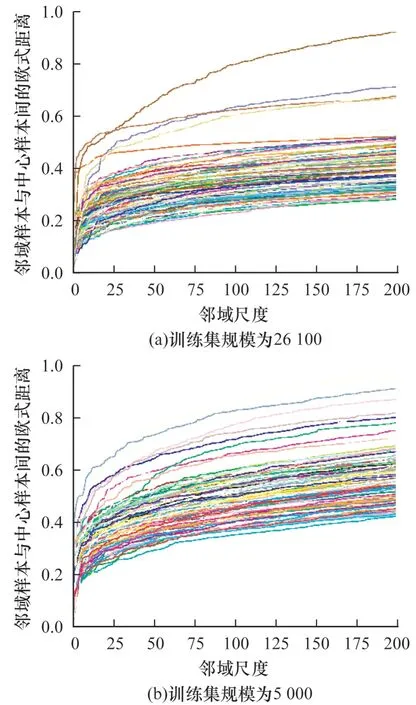
图13 邻域样本与中心样本的距离关系Fig.13 Distance relationship between neighbor sample and center sample
图14 是邻域样本不同尺度数下的预测准确率对比。实验采取的邻域尺度分别为k=22,32,…,n2。尺度数为1 就选邻域尺度为k=22尺度的邻域标记样本作为输入,尺度数为2 就选k=22、32这2 个尺度的邻域标记样本作为输入,依此类推。可以看出,当模型输入取邻域尺度数为4 时,HCNN 模型分类预测准确率最高。
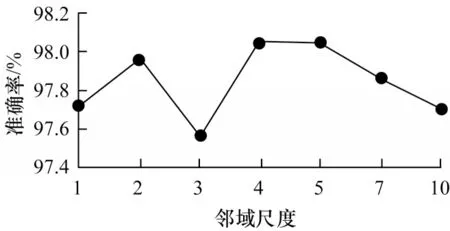
图14 不同邻域尺度下的准确率对比Fig.14 Comparison of accuracy under different neighbor scales
4.3.3 软硬邻域标记的实验对比
在邻域标记样本集中,各属性项是每个邻域样本的标记值(即PM2.5 浓度是否超标,需要将实际的数值通过门限判决转为硬标记,即±1),这样输入到HCNN 模型的数据中就损失了PM2.5 浓度的细节信息,因此,也可以考虑保留各邻域样本的PM2.5 浓度原始值,即软标记值。
图15 为HCNN 算法在邻域标记样本集分别采用软硬标记值的各项指标对比。可以看出,软标记输入所得的各项指标略好于硬标记输入,因此,本文使用邻域样本的软标记值作为模型训练的输入。
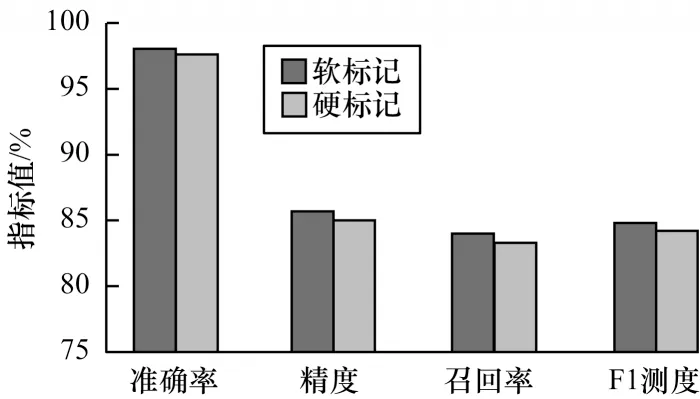
图15 邻域样本软硬标记值的HCNN 性能对比Fig.15 Comparison of HCNN performance with soft and hard labels of neighbor sample
4.3.4 HCNN 算法在混淆样本中的性能分析
由于kNN 算法依靠邻域投票机制进行分类预测,因此往往无法解决混淆样本的分类问题(如图3所示)。在高度不平衡样本集中,这种情况更为突出。为此,分别针对平衡样本集和不平衡样本集对比HCNN 和kNN 算法在不同的混淆条件下的性能,实验结果如图16 所示。
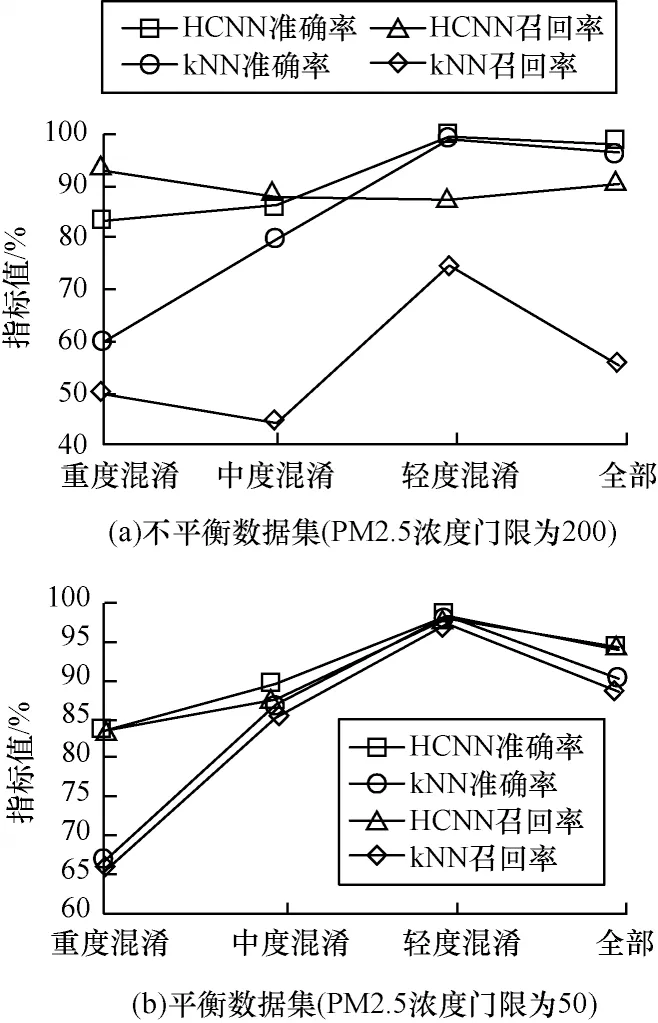
图16 HCNN 与kNN 在不同混淆条件下的预测性能对比Fig.16 Comparison of prediction performance between HCNN and kNN under different confusion conditions
由图16 可以看出,HCNN 对混淆样本的预测效果要远好于kNN 算法,体现了超球卷积在提取复杂邻域标记空间结构特征上的优异能力。
4.3.5 HCNN 与其他算法的性能对比
将HCNN 与kNN、Radar-CNN、FC-CNN、CNN这4 种算法进行性能对比,实验结果如图17 所示。可以看出,HCNN 的预测准确率略高于其他3 种算法,预测精度kNN 最高、HCNN 算法排列第二。由于在不平衡数据集中准确率失真,因此主要对比召回率等指标,可以看出,HCNN 算法显著优于其他算法,体现出HCNN 在不平衡样本集上的性能优势。
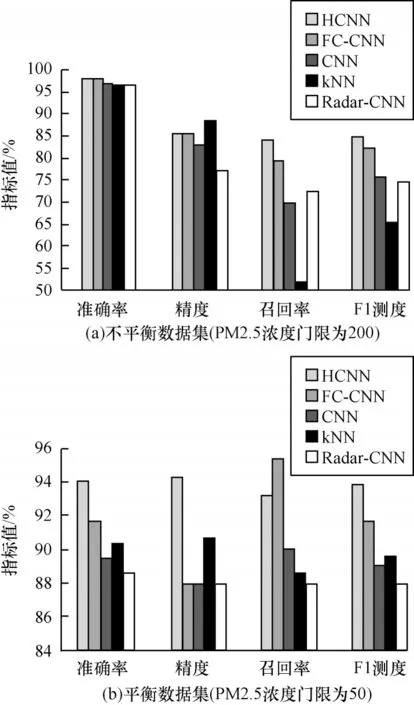
图17 不同算法的性能指标对比Fig.17 Performance comparison of different algorithms
通过与CNN 算法的消融实验对比可以发现,利用kNN 预处理进行近邻结构信息的提取后能够显著提升模型性能,由此可见,对于异质数据集,利用kNN 进行样本同质化是一种有效的手段。
5 结束语
本文提出一种结合kNN 和CNN 的深度学习模型。利用kNN 的近邻搜索,将仅携带多维属性信息的异质数据样本集转化为携带邻域样本标记信息和属性空间结构特征的同质化数据集。在此基础上,通过对邻域样本标记进行超球卷积的方式提取未知样本的邻域标记特征,进而对该样本的标记进行预测。实验结果表明,该模型能够有效提取未知样本的邻域样本标记特征并对该样本的标记进行准确预测,与kNN、CNN、FC-CNN、Radar-CNN 等算法相比预测性能更优。下一步将分析HCNN 在多种数据噪声环境、尺度变换(平移/旋转等)条件下的性能,并验证其在处理多标签分类和回归问题时的预测性能。

