基于时空图卷积网络的交通事故风险预测研究

王庆荣，魏怡萌，朱昌锋，田可可

（1.兰州交通大学 电子与信息工程学院，兰州 730070；2.兰州交通大学 交通运输学院，兰州 730070）

0 概述

随着科技和社会的发展与进步，车辆和道路在增加，交通事故发生的频率也在不断增加，人们的生命和财产受到严重威胁［1］。预测交通是一项具有挑战性的任务，虽然日常通勤是相对可预测的，但在节假日、休闲活动、恶劣天气等情况下的交通出行均具有很强的随机性，较难预测。目前，通过交通大数据预测交通事故风险成为研究热点，如果能准确预测交通事故，并根据预测结果对交通事故的发生进行重新规划，那么将提高城市交通效率，减少交通事故的发生导致的城市、个人经济损失，同时也能保障人们的人身安全。

目前，研究人员对交通事故预测方面的研究可以分为两大类。第一类是传统预测方法，比如统计回归法、灰色预测法等。传统回归法常用于短期数据变化的预测，但对于随机性较大、干扰因素较多的交通数据来说，其预测的结果比较片面，可靠性难以得到保障。灰色预测法适用于样本数量较少的预测，其模型简单，对中短期预测有较好的预测结果，但对于中长期的预测仍有不足。第二类是神经网络预测法，该方法的自主学习能力较好，非线性映射和高鲁棒性也较强，在交通预测领域的应用前景较广泛。虽然现有对交通事故的预测研究已有较好的成果，但交通事故的发生受很多复杂因素影响，如驾驶员的行为等不可控因素给交通事故的预测增加了很多困难，交通事故的复杂机制依旧不太明确。

经典的机器学习技术大多将交通事故的预测看作分类问题，目的是预测下个时段是否会发生交通事故，未考虑相关复杂因素的影响，因此预测结果相对较差。文献［2］使用逻辑回归方法对美国4 号洲际公里的交通事故进行预测，文献［3］提出连续的非凸优化的k-means 算法，通过一个等效模型，利用矩阵优化理论分析和解决交通预测模型问题。文献［4］通过动态预测模型建立基于马尔可夫链和云模型预测道路交通事故的数量。文献［5］提出使用多层感知器模型预测事故热点地区的事故情况。文献［6］提出基于反向传播（Back Propagotion，BP）神经网络的高速公路事故预测，但BP 神经网络的缺点是易陷入局部最小点，收敛速度较慢，训练时间也较长。文献［7］提出一个组合预测优化模型预测交通事故，以提高预测精度，但在如何更好地结合单一模型方面还有待提高。文献［8］提出灰色BP 神经网络模型预测发生交通事故后的车型分担率，并结合BP 神经网络模型和灰色预测模型进行优势互补，相比单纯的BP 神经网络有较高的预测精度和稳定性。文献［9］建立了基于改进深度森林算法的交通事故风险状态等级预测模型，通过对比传统预测模型验证该模型的优势。文献［10］通过引入交通风险概念，建立一个堆叠自编码器模型，研究在城市道路中过往人流量的变化对交通事故风险的影响。文献［11］对长短期记忆（Long Short-Term Memory，LSTM）模型进行改进后提出双尺度LSTM 模型，用以预测交通事故，并得到了很好的效果，但混合模型的训练时间较长，且未考虑复杂的天气、路况等影响因素。

文献［12］提出一种新的堆栈去噪卷积自动编码模型用于预测城市交通事故风险，并使用空间依赖性学习事故中的隐藏因素，实验表明该模型的性能优越，但该模型未考虑天气因素的影响。文献［13］提出一种基于时空注意力网络的区域交通事故风险预测深度学习框架，并综合影响交通事故的外部因素，提高了模型的预测性能。文献［14］提出基于卷积神经网络的车边缘网络，用于交通事故风险预测，经过实验对比发现，该网络的精度较传统机器学习网络较高。文献［15］提出基于路网结构预测短期城市交通事故，采用多层图卷积神经网络和双链LSTM 构建预测模型，发现时空特征属性对最终的预测结果影响较大，但该模型存在多源数据和因子分析缺乏的问题。

综上可知，目前交通事故风险预测的研究主要存在以下几点问题：一是未考虑在实际场景下，发生交通事故的多源外部影响因素，如车流量、路况、天气、兴趣点（POI）等；二是未考虑时空特征对交通事故产生的影响；三是现有研究大部分是对交通事故量预测的研究，在交通事故风险预测方面的研究较少。

本文采用神经网络方法构建基于时空特征的交通事故风险预测模型，在考虑时间依赖、空间依赖、时空依赖的情况下，在模型中使用改进的时空图卷积网络（Improved Spatio-Temporal Graph Convolutional Network，ISTGCN），通过添加批标准化（Batch Normalization，BN）层解决梯度消失爆炸问题，并采用均方误差（Mean Squared Error，MSE）损失函数，解决样本零膨胀问题。

1 图卷积网络

图卷积网络（Graph Convolutional Network，GCN）［16］和卷积神经网络（Convolutional Neural Networks，CNN）均可以作为特征提取器，但GCN 的对象是图数据，其先从图数据中提取相关特征，然后用这些特征对图数据进行结点分类、图分类、边预测等。一个图的结构如式（1）所示：

2 ISTGCN 模型

2.1 时空图卷积网络的结构

时空图卷积网络（Spatic-Temporal Graph Convolutional Network，STGCN）在交通中的应用最开始用于交通事故预测，后来逐渐被学者应用于交通流［17］的预测。由于交通流和交通事故均在一定的空间和时间背景下发生，因此均会受到时空特性相关复杂因素的影响，且交通事故相比于交通流受时空特性的影响更大，且交通流也是交通事故的一个影响因素。本文将STGCN 网络用于交通事故预测中，并验证其预测性能。

STGCN 网络的输入是N×C×V×T，先通过尺寸为1×1 的2d 卷积层输出N×(C×K)×V×T，再与邻接矩阵A(K×V×V)相乘，这里K表示子集的个数，得到空间卷积N×C×T×V，最后通过一个定义的时间长度n_t×1，2d 卷积层进行时间维度的卷积。其中：N为个数；C为通道数，即特征维度；V为顶点个数；T为时间维度。STGCN 网络的结构如图1 所示。

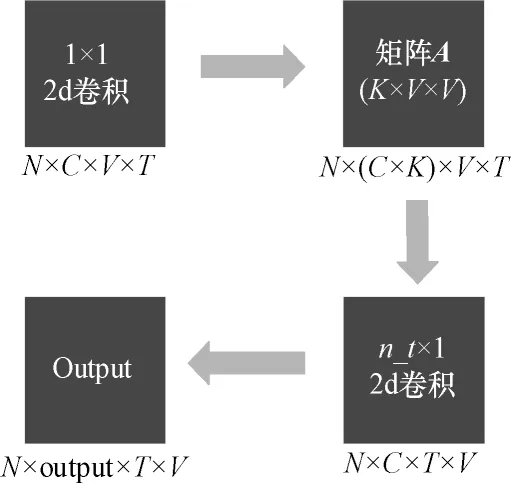
图1 STGCN 网络的基本结构Fig.1 Structure of STGCN network

交通事故的致因主要分为空间相关性、时间相关性和时空相关性三大类，本文对每类因素的不同特征采取不同的网络结构，依次进行特征提取，并将处理后的相关数据放入本文模型中进行训练。

2.2 ISTGCN 模型框架

ISTGCN 模型由2 个时空卷积模块和1 个全连接层组成，时空卷积块的每个模块有2 个时间门控序列卷积层和中间1 个空间卷积模块，如图2 所示为本文模型的结构。首先使用GCN 网络提取相关特征的空间属性，然后使用门控线性单元（Gated Linear Units，GLU）来建模事故的相关时间依赖，最后通过时空卷积模块，并利用图形和卷积捕捉时空特征的相关动态变化。此外，以构造好的时空相关属性的图信号权重矩阵作为输入，通过时空卷积模块的时空相关性预测模块，并将前3 个模块的输出进行加权融合，输出最终的预测值。

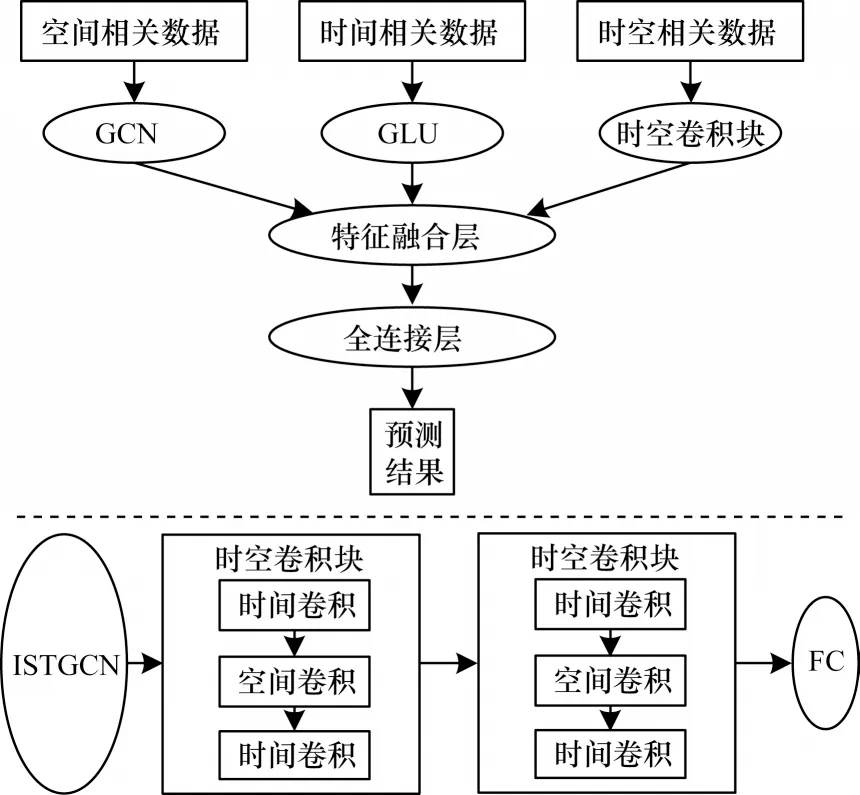
图2 ISTGCN 模型结构Fig.2 Structure of ISTGCN model

空间卷积层由图形卷积组成，该卷积将路段及其邻域的空间信息聚合在一起。时间卷积层在图形卷积操作上捕获时间维度的标准卷积层，并通过合并连续时隙中的有效信息以更新各个节点的有效信号。使用空间图形卷积捕获空间相关属性，利用时间门控卷积捕获时间相关属性，并采用时空卷积块融合空间域和时间域的特征。

为解决梯度爆炸问题，本文在模型中加入BN层，并采用MSE 损失函数，在计算损失时，对交通事故风险较大的样本给予较大的权重，避免模型预测结果聚集在0 附近。

2.2.1 空间卷积模块

在一般情况下，用图形结构表示交通网络，用数学公式表示路网。以往的研究忽略了交通网络的空间属性，交通网络常被分为多个分段或网络，导致网络的连通性和整体性被破坏。本文模型将直接在图形结构数据上使用图形卷积，用来提取空间域中有意义的特征，并计算图卷积中的核Θ。由于图傅里叶基数［18］运算代价较高，因此采用切比雪夫多项式［19］逼近策略来克服该问题。

选择几个空间卷积空间段组成空间分量，选用相应的表示形式，并通过全连接（Fully Connected FC）层略微减小空间特征。然后，将特征输入到堆叠的空间卷积块中，一个空间卷积块由几个空间卷积层组成，聚集了路段与领域的空间信息，通过在该空间卷积层中加入BN 层来增加模型初始化的健壮性，提升训练速度与分类效果。BN 层对于初始化的要求不高，所以可以使用较大的学习率进行训练，假设第1 层的输入和输出分别为H(L)∈RN×F和H(l+1)∈RN×F，则空间卷积层的计算式如式（4）所示：

其中：BN 是标准归一化；ReLU 为激活函数；H是可训练参数。

2.2.2 时间卷积模块

通过门控线性单元（Gated Linear Unit，GLU）提取时间相关属性，相比LSTM 来说，GLU 模型更加简单，收敛速度更快，需要的op（Operation）更少，这样一来，模型所需非线性的操作也就更少，因此能够有效降低梯度弥散现象，提高模型训练及收敛速度。

在时间维度上采用一维因果卷积对数据进行并行处理，采用GLU 实现时间维度上的卷积操作，在每个节点上使用GLU 捕获时间上的依赖关系。首先在CNN 的卷积层中引入门控线性单元机制，使卷积层的输出变成式（5）所示，表示一个没有非线性函数的卷积层输出，再通过Relu 非线性激活函数的卷积层输出，表达式如式（5）所示：

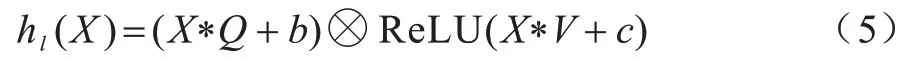
其中：X是层hl的输入，即前一层的输出；Q和V 表示不同的卷积核；n表示输出通道数；b和c为偏置参数。式（5）后半部分含激活函数的卷积，即门控机制，其控制了X*Q+b当中的哪些有效信息可以传去下一层，然后将该模型进行堆叠以便获取时间相关属性。在获取空间维度上各个节点的相邻信息时，采用基于图形卷积操作上的时间卷积层，通过合并连续时隙中的信息来更新节点信息。

时间特征可以反映每个路段的历史交通状况，第1 个时间卷积层的第vi路况的输入信号为，输入信号的第j通道的计算式如式（6）所示：

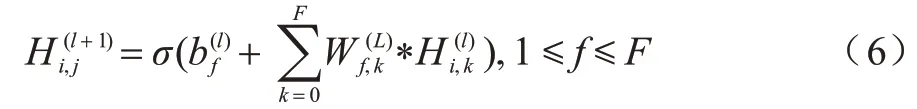
2.2.3 时空卷积模块

本文构造了时空卷积块（Spatio-Temporal Convolutional Block，ST-Conv）以联合处理图结构时间序列，融合时空域的特征。ST-Conv 利用图形和卷积捕捉空间和时间相关特征属性的动态变化，时空卷积模块可以根据特定情况的规模和复杂性进行堆叠和扩展。一个空间卷积块由2 个时间卷积核和1 个空间层组成，空间卷积层是连接2 个时间卷积层的桥梁，通过时间卷积层可以实现图卷积到时间卷积的快速时空传播［20］。

将GCN 网络与加入CNN 的门控线性单元GLU组合成ST-Conv，把输入的数据先做时间维度的卷积，将时间维度卷积的输出结果再做图卷积操作，图卷积的输出结果经过1 个Relu 之后再进行1 个时间维度卷积，以上即为整个ST-Conv 的输出。

此外，本文使用Relu 激活函数，在叠加2 个ST-Conv 之后增加1 个额外的时域卷积层，并和1 个全连通层共同作为输出层，以防止过拟合，ST-Conv的输入和输出都是3D 的张量。

2.2.4 融合预测模块

堆叠2 个时空卷积模块及1 个时间卷积模块的输出后，通过拼接操作将空间、时间、时空以及外部信息融合在一起，形成一个融合的表示，将融合后的表示输入，得到输出层，并使用式（7）进行融合：

其中：*表示卷积操作；W1，W2，W3为卷积核参数；Y1，Y2，Y3为3 个模块的输出；FC 为全连接层，输出结果Y∈RI×J是下一个阶段发生交通事故的风险。

在交通大数据中，交通事故数据与交通流数据存在较大差别，例如交通事故样本中会出现“零值”，代表伤害程度最低等级，比如未受伤。研究结果表明，当事故样本中含有大量的零值时，容易导致各影响因素对“零值”的边际概率被高估，若忽略这种零膨胀现象，将导致有偏估计，从而导致错误的结论［21］。因此，本文采用MSE 损失函数解决数据零膨胀问题，在计算损失时给予事故风险样本较大的权重值，以避免预测值在0 附近。本文将事故风险分为3个等级（轻度、中度和重度），对应的风险值i分别为1、2、3，计算式如式（8）所示：

其中：Y表示真实值；Y'表示预测值；λi代表权重值（事故风险等级为i的样本权重）。

本文模型的流程如图3 所示。

图3 本文模型的流程Fig.3 Procedure of model in this paper

3 实验结果与分析

3.1 数据来源与分析

选用Kaggle 上的2005～2018 年英国道路安全交通事故和车辆公开数据集，该数据集是实时收集的，使用了多个流量应用程序编程接口（Application Programming Interface，API）。这些API 广播各种实体捕捉到的交通事件，比如英国和国家运输部门、执法机构、交通摄像头以及道路网络内的交通传感器，目前该数据集大约包含120 000 起事故记录。本文选取了2005～2018 年期间部分事故数据进行验证，并从2018 年1 月到2018 年12 月的全英国事故中，挑出部分事故严重的时间段进行了可视化，统计分析图如图4 所示。

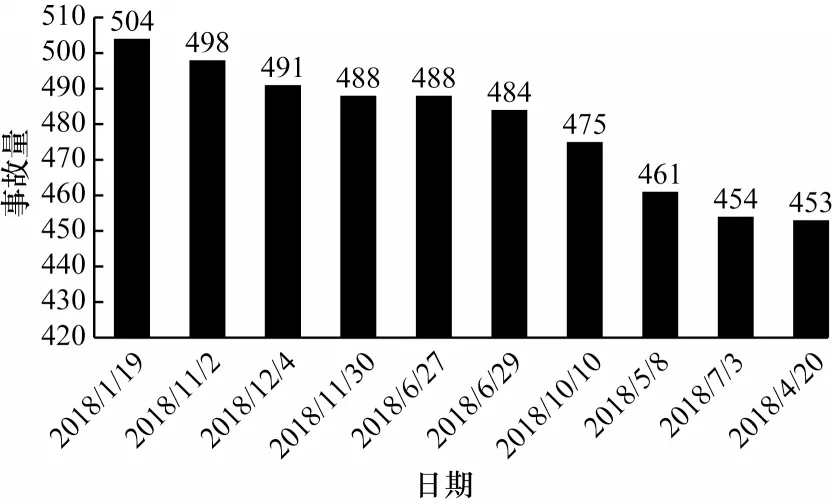
图4 不同时间下的交通事故量Fig.4 Traffic accidents at different time

本文收集的数据集均是英国的交通事故量、交通流量、天气数据，此数据集一共包含32 条属性，包括事故记录ID、严重程度、开始时间、结束时间、温度、经纬度、风向等。所选取数据的具体分类如下：

1）交通事故。该数据包含了2005～2018 年期间所有记录的交通事故。除了街道相关信息、时间、地点等一些基本信息外，该数据集还包括撞车的原因。本文把数据集按事故严重程度等级划分为1，2，3，数值越小，表示事故越严重，该数据集不同风险等级下的交通事故量统计如图5 所示。

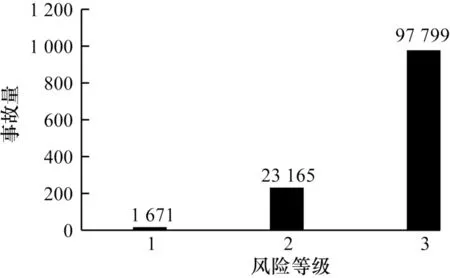
图5 不同风险等级下的交通事故量Fig.5 Traffic accidents quantity under different risk levels

2）交通流量数据。由相关识别设备检测到的行车记录计算而来，行车记录包括设备ID、车牌号、车辆过车时间、方向、车道号5 个属性，正常路段车速对交通事故的影响如图6 所示。

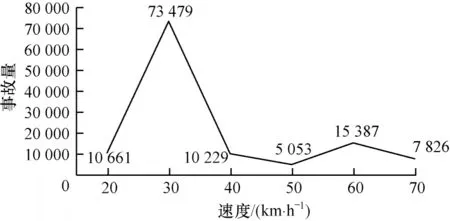
图6 交通事故量与速度的关系Fig.6 Relationship between traffic accidents volume and speed

3）天气数据。本文采集的天气数据来自英国天气数据中心，数据属性有时间、天气、经纬度、能见度、湿度、温度、风向等。天气状况对交通事故的影响如图7 所示。对天气状况进行标签化，将天气条件恶劣程度等级划分为-1～9，数值越小，表示天气越恶劣。由图7 可以看出天气条件严重恶劣情况下造成的交通事故量最多。

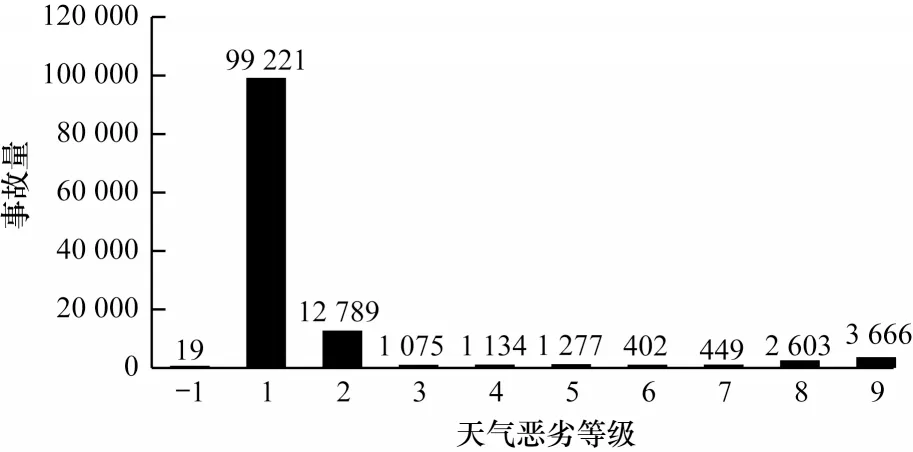
图7 交通事故量与天气的关系Fig.7 Relationship between traffic accidents volume and weather

4）POI 数据，POI 数据也来自英国公共数据中心，包含学校、购物中心等的POI 坐标。

3.2 数据预处理

对收集到的数据进行去除冗余值、补全缺失值等预处理操作之后，将其转化为权重矩阵的形式，并作为模型空间预测单元的输入。数据对象每一个属性权重都是该权重占所有权重的比例，定义一个二元空间对称矩阵H，以此来表达n个节点位置区域的相邻关系，如式（9）所示：

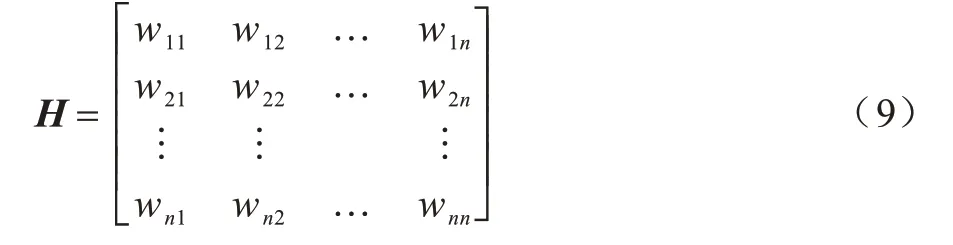
其中：wi j指的是第i行数据对象的第j个属性占所有属性的比例。

图8 为构造图形结构［22］的数据权重矩阵，数据点vt为一个图形信号，该图形信号定义在无向图G=(vt，ε，w)上，其权重为图8 的wi j，vt是一组有向的顶点，对应于交通道路网络中监测站的观测值，ε表示站与站之间连通的一组边。

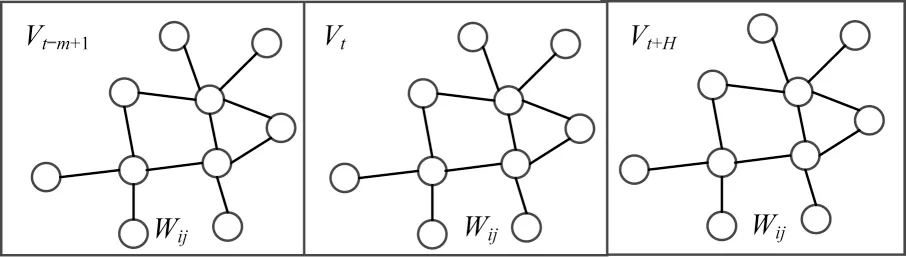
图8 图形结构的数据权重矩阵Fig.8 Data weight matrix of the graph structure

3.3 评价指标

本文使用平均相对误差（Mean Relative Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、召回率（Recall）等评价指标评估预测模型，相关计算式如下所示：

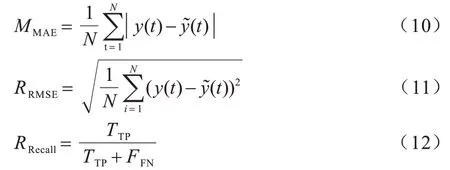
其中：y(t)为t时刻交通事故的实测值；(t)为预测值；N为样本个数；TTP表示实则为正类且预测为正类的样本数目；FFN表示实则为正类且预测为负类的样本数目。

3.4 结果分析

本文实验在Python3.6 和TensorFlow1.9 的环境下进行，将所选用数据集的交通流量、交通事故量、外部特征属性作为训练输入，2018 年的交通流量、外部特征作为预测模型输入，模型输出交通事故量。在实验中，按照时间顺序以6∶2∶2 的比例划分训练集、验证集、测试集。基于TensorFlow 框架实现ISTGCN 模型，经过实验比较，使用3 层图卷积，卷积核大小均为3；GLU 为3 层，每层隐藏单元个数为128，使用BN 层将数据归一化。每个实验包含7 个对比交通事故预测模型：历史平均HA 模型（利用相同时段事故风险的平均值预测下一时段的事故风险）、基于提升树的机器学习（XGBoot）模型［23］、多层感知机（Multilayer Perceptron，MLP）模型、门控循环单元网络（Gate Linear Unit，GLU）模型［24］、基于CNN的堆叠降噪自动编码器模型、CNN 和LSTM 相结合（ConvLSTM）模 型［25］和本文 所提出 的ISTGCN模型。

3.4.1 对比实验分析

将本文模型和对比模型在英国真实数据集上进行预测分析，分别迭代200 次和300 次，所有对比模型均在同一数据集下进行调试，结果如表1 所示。由表1 可以看出，迭代300 次的整体预测结果比迭代200 次的好，HA、XGBoot、MLP 和GLU 模型的整体预测效果都比较差，这些模型均没有捕获空间特性。SDCAE 模型较HA、XGBoot、MLP 和GLU4 个模型的整体预测效果较好，但却忽略了时间的长短期相关性。ConvLSTM 模型同时考虑了时间和空间相关属性依赖，但却忽略了时空特性对交通事故预测的影响，相比之下，本文ISTGCN 模型在同时考虑时间、空间、时空相关属性依赖后，取得了较好的预测结果。

表1 不同模型的结果对比Table 1 Results comparison of different models

3.4.2 模型结构分析

对本文ISTGCN 模型的模块结构进行对比分析，在去掉空间层和时空层后，对剩下结构进行模型预测训练。由于模型在迭代300 次时效果最好，因此本文结构分析分别是在迭代300 次后的预测结果，预测结果如表2 所示，其中S、ST 分别代表空间层和时空层。由表2 可以看出，ISTGCN 模型的每块结构都有不同的作用性能，去除任一模块结构，得到的预测结果都很差，ISTGCN 模型采用空间层获取空间相关属性，使用时间层获取时间相关属性，利用时空卷积层捕获时空相关特征，只有这3 种结构相互作用，才能得到最佳性能。为验证ITSGCN 模型性能，使用运行时间消耗这一指标进行性能分析，表3 所示为不同模块结构训练时间的对比，本文模型ISTGCN 实现了更快的训练速度，在去除任意结构之后性能表现都不佳，只有3 种结构彼此相互作用，才能实现最佳性能。

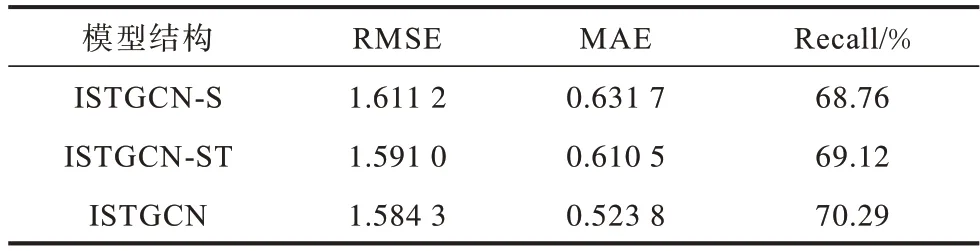
表2 本文模型结构对预测性能的影响Table 2 Influence of structure of model in this paper on prediction performance

表3 数据集训练时间消耗Table 3 Training time consumption of data sets 单位：s

3.4.3 激活函数分析

分别用3 种不同激活函数验证模型性能，迭代次数选择300 次，对比在激活函数前和激活函数后加入BN 层的变化，激活函数对模型预测性能的影响结果如表4 所示。由表4 可以看出，当激活函数为ReLU 的时候，预测性能整体较好，将BN 层加在激活函数前比加在激活函数之后效果更好，这是因为卷积层在进行BN 操作时，会把数据分布在指定的区间，当ReLU 函数再进行激活操作时，神经元失活的概率会下降，模型性能得到较大幅度的提升。

表4 激活函数对模型预测性能的影响Table 4 Impact of activation functions on predictive performance

如果先在ReLU 函数后进行BN 操作，ReLU 函数激活后的部分神经元已失活，参与BN 操作时的神经元数量就会减少，模型的泛化能力降低。由表4 也可以看出ReLU 函数在BN 层前后的变化并没有Sigmoid 和Tanh 函数变化大，这是由于BN 层在ReLU 函数前可以让ReLU 函数更好地产生特征选择作用，由于输入值的分布更接近于零均值，此时ReLU 函数可以展现单侧抑制作用，且不会出现输入全分布在0 的一侧。但如果将BN 操作放在ReLU 函数之后，在激活函数后进行归一化能更好地保证下一层的输入是零均值，能避免下一层连接权重的梯度同号，模型训练效率更高，收敛更快。由表5 结果可知，将ReLU 函数放在BN 前后的差别不大，但也因不同实验而有区别。

4 结束语

本文提出一种基于时空图卷积的交通事故风险预测模型，以多源异构数据作为输入，分别基于空间卷积层、时间卷积层和时空卷积层处理不同类型的特征，并将处理后的隐含特征拼接成紧凑的表示，馈入全连接层，学习不同特征之间的相互作用，预测下一个阶段的交通事故风险。在空间卷积层中加入BN 层，解决梯度爆炸问题，应用MSE 损失函数来解决数据零膨胀问题。在英国真实数据集上的实验结果表明，与GLU、SDCAE、ConvLSTM 模型相比，该模型的RMSE 指标分别降低3.28%、4.87%、4.19%。下一步将优化网络结构与参数，通过收集违章、行人、出租车等数据，训练并优化模型，提高模型的运行速度和预测效率。