基于曲率和的主动声呐干涉条纹特征表征方法

孙同晶，闫志明，范 军，张 豪

（1.杭州电子科技大学 自动化学院，杭州 310018；2.上海交通大学 海洋工程国家重点实验室，上海 200240）

0 概述

声波在浅水域中的传播是一种很复杂的现象，受水中噪声及水底环境的影响，各传播模式之间相互干扰，声波与信道边界之间相互作用，从而导致信号衰减和多径传播，这种传播所产生的时频或时空结构可生成恒定强度的干涉条纹。被动声呐所产生的声场的条纹结构表现为频率-距离方向上斜率恒定的直线，CHUPROV［1］提出波导不变量的概念来表述这一恒定斜率的条纹结构，KUPERMAN 等［2-4］通过群慢度差和相慢度差来近似求解波导不变量的值，田玲爱［5］根据Hough 变换图像处理的方法提取到条纹特征，安良等［6］利用二维傅里叶脊计算波导不变量的值。但在主动声呐研究中，由于目标散射回波的多路径效应，不同简正波相互叠加，生成频率-距离方向上弯曲的条纹结构，对这种条纹结构特征进行表述难度较高。QUIJANO等［7-9］对主动声呐干涉现象进行研究，尝试通过在水深、声速剖面与高信噪比条件下研究主动声呐波导不变性原理，并首次提出基于广义Hough 变换［10］估计条纹图中不变量参数的方法，该方法得到了条纹特征的分布形式，但是未能给出具体的数值。

曲率信息反映了图像中曲线的纹理特征。刘军［11］利用曲率的计算方式进行车道线检测，对于曲线上离散点的曲率，可通过参数方程［12］进行求解。本文提出曲率和的概念，即对曲线上离散点曲率值进行求和，以刻画曲线的总体弯曲程度。通过基于离散点曲率和估计条纹图中特征的方法，可得出某一频段内条纹结构的变化，且提取出的条纹特征值可作为主动声呐波导不变量［13-15］的重要参考。

1 主动声呐声场干涉结构

在浅海波导中，设声源深度为zs，接收器深度为zr，声源发射一个宽带脉冲信号，经过海洋波导传播后，传到深度为zt的目标，经目标散射［16-17］后由接收器接收。接收点处的声压场写成简正波模式［16］，如下：

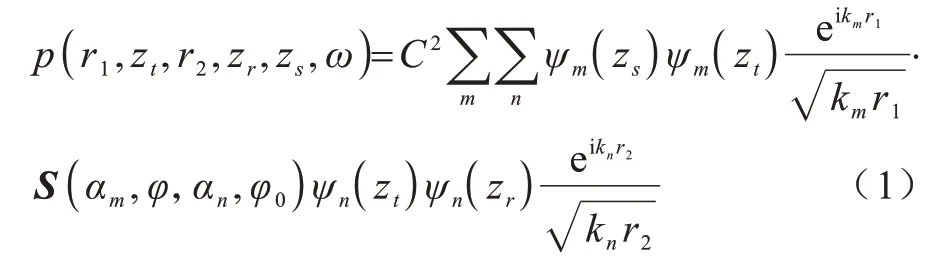
其中：C=为常数；r1、r2分别为声源到目标、目标到接收器的距离；ω是声波频率；S(αm，φ，αn，φ0)表示散射矩阵；km是第m个信道传播的水平波束，kn是第n个信道传播的水平波束；ψm是入射模态相关的模式函数；ψm(zs)是发射声源深度相关的模式函数；ψm(zt)是目标深度相关的模式函数；ψn是反射模态相关的模式函数；ψn(zt)是反射模态中目标深度相关的模式函数；ψn(zr)是反射模态中接收器深度相关的模式函数。

假设海面绝对软且海底为绝对硬的刚性海底，根据海底和海面边界条件得到模态函数表达式［18］如下：

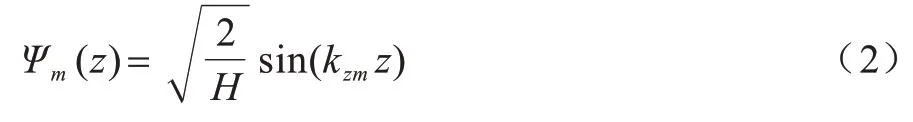
其中：H为水深；z代表物体摆放深度。根据接收点处声压场的计算，可得到信号传播过程中频率-距离干涉条纹图。

2 离散点曲率数值计算

对于曲线y=f(x)，可知二维平面中曲线曲率标量形式［19］表示为：

在曲线表达式已知的情况下，可以直接对曲线表达式进行解析求导。当曲线表达式未知时，本文采用离散点曲率的方法进行求解，选取曲线上3 个点，使用由3 个点确定的二次曲线的曲率作为待求曲率，曲线上选取3 个点，要求3 个点之间的距离尽可能近，以中间点处的曲率作为3 个点的曲率估计［20-23］。离散点曲率估计曲线如图1 所示。

将图1 中曲线t用参数方程表示为：

上述参数方程可转化为根据已知3 个点求解参数(a1，a2，a3)以及(b1，b2，b3)的问题。为求得参数方程的解析解［13］，使用曲线中3 个点的矢量长度作为t的取值范围：

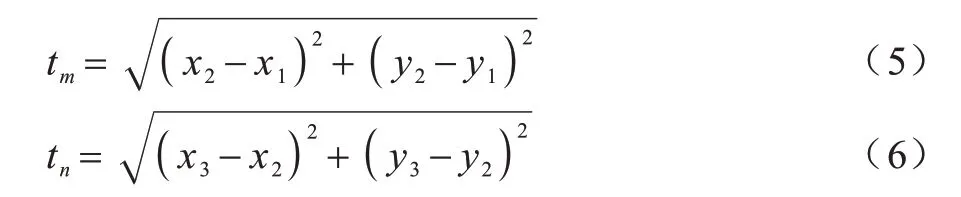
对于曲线上的3 个点，满足条件：

根据边界条件，代入曲线上的3 个点，可将式（4）表示为：

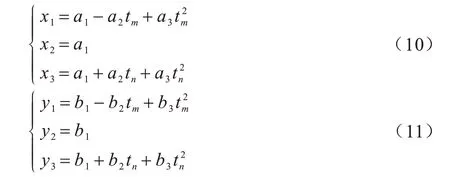
式（10）、式（11）为三元一次方程组，将它们写成矩阵的形式：

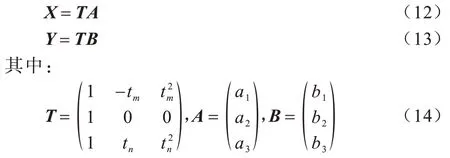
根据矩阵求逆运算公式，可求得A和B的值，至此曲线方程转换为t的函数，根据求解一般曲率的表达式（式（3）），在t=0 处分别求出x和y的一阶导数与二阶导数：

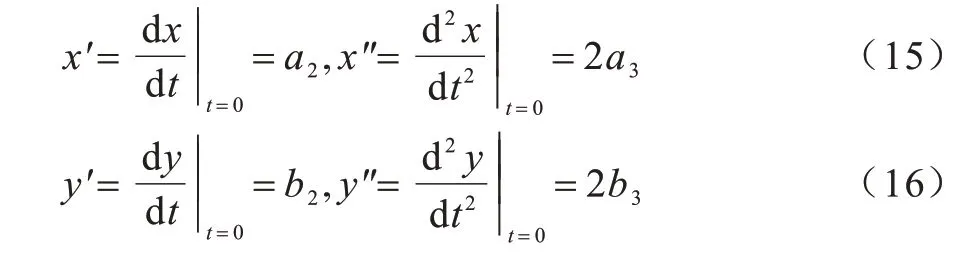
将式（15）和式（16）代入式（3）可得：

根据式（17）可计算出曲线上一点处的曲率值，由图1 生成的主动声呐频率-距离干涉条纹图，选取曲线上的离散点进行计算，可得到离散点曲率值。本文通过量化单位频率内条纹曲线的曲率和来表征这一范围内曲线的弯曲程度，并用于表述主动声呐干涉条纹的特征。

3 主动声呐条纹特征及表征

本节根据式（1）的声场模型对声场干涉条纹结构进行仿真，然后通过曲率和的求解得到条纹特征信息。

3.1 理想波导中球体目标干涉条纹仿真

在理想波导条件下进行仿真，如图2 所示，海底距水面深度为50 m，发射器与接收器距水面7 m，目标深度为7 m，目标在距离发射器50 m 的范围内往返移动，发射频率段为40～80 kHz，理想波导采用海面为绝对软、海底为绝对硬的介质，计算出接收器处声压场的变化情况，可得到理想波导条件下目标移动过程中频率-距离的变化关系。图3 所示为根据声场模型得到的频率-距离干涉条纹，为探究不同频率对干涉结构的影响，仿真结果分为不同的频率段。

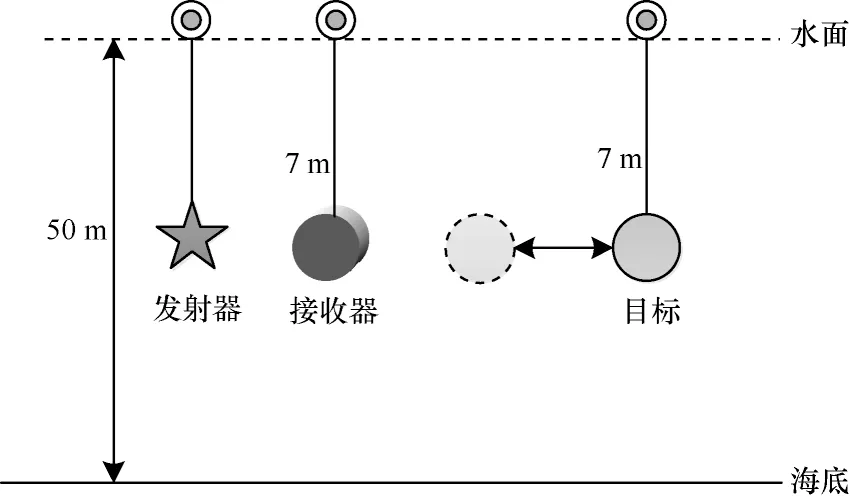
图2 理想波导仿真场景Fig.2 Ideal waveguide simulation scenario

图3 主动声呐频率-距离干涉条纹Fig.3 Interference fringe of active sonar frequency-distance

从图3 可以看到明显的亮暗相间的干涉条纹，且这些条纹由曲线构成，通过分析条纹的曲率可得到条纹特征。

3.2 基于曲率和的条纹特征表征

本文取不同频率段的声场干涉条纹图进行分析。为得到条纹特征，需要对条纹曲线进行处理，选取图中的标记曲线计算干涉条纹特征。由于条纹的弯曲程度在不同频率上会发生变化，因此将图像所在频率分成3 份并分别提取曲率特征，最后取不同频段上曲率的平均值。可根据图3 提取曲线上的点计算每一点处的曲率变化，曲率变化反映了条纹特征的大小，根据式（17）可得不同频段的曲率值变化关系。

图4 反映了不同频率段曲率的变化轨迹，其中，箭头表示曲线上一点处曲率的标量大小，由图4 可知，曲线弯曲处曲率值较大，表现为波谷处箭头密集且长度最长，而当曲线弯曲程度较小时，表现为图中箭头稀疏且长度较小，由此可得到干涉条纹曲率变化的量化关系。在40～80 kHz 频段内，随着频率的增大，干涉条纹曲率和呈现减小的趋势，最后取不同频段条纹曲率特征的平均值，计算可得3 个频率段上的平均曲率和为0.653。调整接收器的深度，利用相同的方法分别模拟不同深度处的接收器声压信号，得到不同深度处曲率和的平均值，结果如表1 所示。从表1 可以看出，接收器位于不同深度时提取到的曲率和有所变化，计算结果均在0.6 附近，这说明用曲率和的形式表述条纹特征值具有可行性。表1 中展示的曲率和随深度变化有规律可循，当接收器与目标位于同一深度时，表现为此时的曲率和接近最大值，实验证明这种方法可以较稳定地表示干涉条纹谱图中的条纹特征，充分地利用了微分几何中曲率不变的特性，能够同时体现条纹谱图的宏观和微观特征信息，最后利用曲率和的概念表示条纹特征信息，可作为提取主动声呐干涉条纹特征的一种衡量标准。

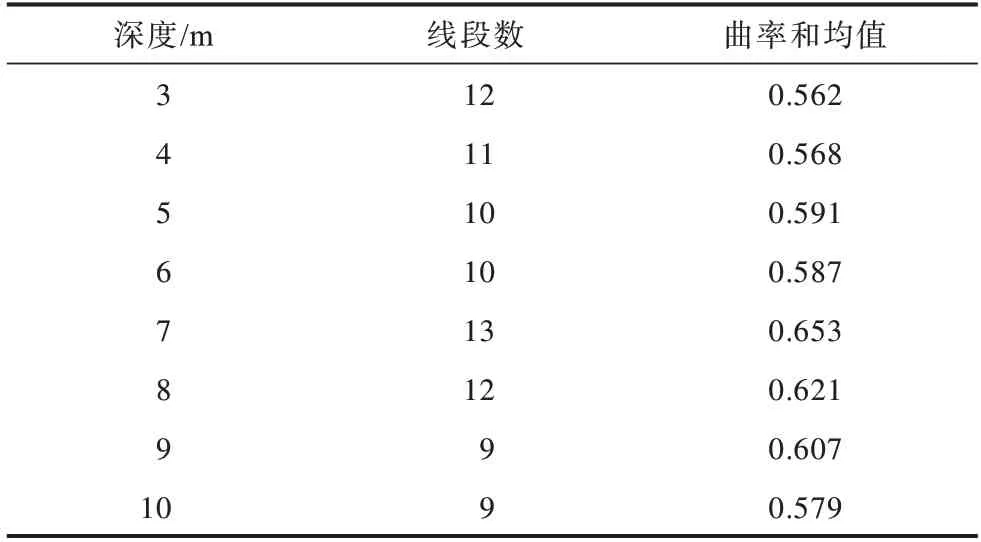
表1 接收器位于不同深度时的平均曲率和Table 1 The average sum of curvature extracted by the receiver at different depths

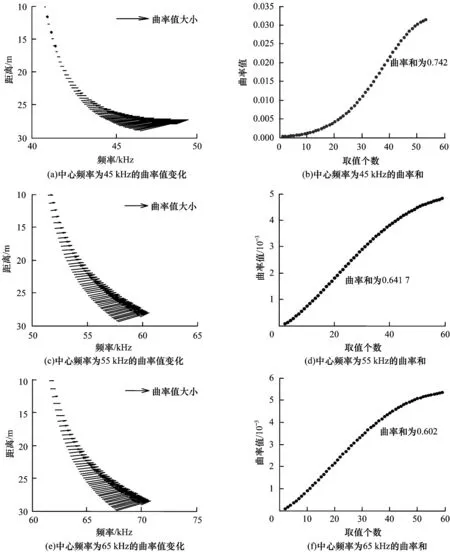
图4 不同频率段的曲率值变化关系Fig.4 Variation of curvature values in different frequency bands

4 基于实测数据的条纹特征分析

本次实验在莫干山湖泊进行，莫干山湖泊水深14 m，水底为泥沙水质，湖面开阔，水体环境及水声传播特性近似为浅海波导环境。发射阵距目标50 m，发射信号为线性调频信号，发射换能器和目标均处于水下7 m，声源频率f为40～80 kHz 频段，脉宽为2 ms，目标模型是半径为1.2 m 的刚性球，采用4 个标准水听器，接收共采用26 个通道，接收器通道深度为7 m。

获取到水声回波采集信号如图5（a）所示。第3 节仿真中选取了目标单向移动时接收器处的声压进行处理，但在实测数据中目标是往复运动的，获取到的回波信号为目标往复运动的结果，而且由于仿真中考虑的信号较为简单，选择不含噪声的数据进行处理，而实测数据中还会出现噪声干扰和较高的混响，因此，需要对回波信号进行处理，采用匹配滤波［24-26］的方法可以很好地对回波信号进行预处理，预处理后的回波信号如图5（b）所示。图5（a）中第1 个峰值为主动声呐直达波信号，第2 个峰值为目标回波信号。因为会有水底反射波的干扰，所以对目标回波信号进行处理，得到图5（b）对应的轨迹图，可以看出，第50 个脉冲到第250 个脉冲之间的目标信号较强，并且没有直达波的干扰。为了获得目标的频率-距离条纹特征，取该距离段的信号进行分析，对提取后的回波信号进行时频变换，得到声场干涉谱图如图6 所示。

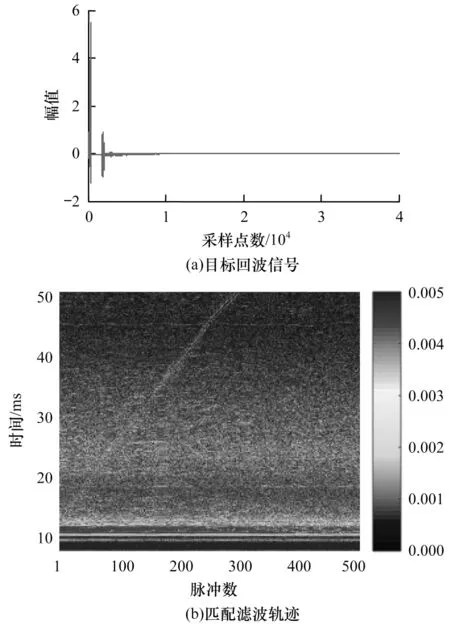
图5 信号预处理结果Fig.5 Signal preprocessing results

图6 实测信号干涉条纹Fig.6 Interference fringe of measured signal

图6 是水听器接收到的声压信号经过滤波器预处理后的声场干涉条纹，从中可以看出明显近似曲线的干涉条纹，波导中存在散射体时，声信号不仅在传输过程中存在色散效应，还会被散射体散射，接收信号频谱在原波导影响后的频谱上叠加散射特征，使得低频频谱产生畸变，表现在图6 中会产生频率的偏移，使得低频部分信号变得不清晰，但中频段简正波能量较为集中，主要信息仍能反映波导中被目标散射后的特征。

为得到干涉条纹的特征信息，将距离-频率干涉条纹分为多个频段，选取相同距离处频段的一条干涉条纹曲线进行处理，得到的曲率值分布如图7 所示。根据曲率累计和可求得图7 中的曲率和为0.512，实验数据对比仿真数据表现为曲率和偏小，这主要与声源-接收阵间距离的测量误差有关，水底环境、散射以及声速剖面随距离的变化均会对接收信号产生一定的影响。

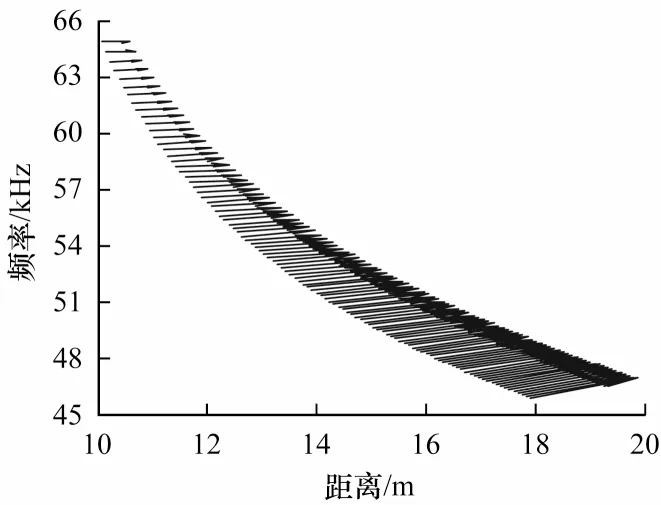
图7 实测曲率变化情况Fig.7 Measured curvature change

5 结束语

主动声呐声场强度生成频率-距离平面上的干涉条纹，其结构反映了简正模色散和相干特性，并具有一定的稳定性。本文对仿真数据进行分析，利用离散点曲率和的形式表述条纹特征，主动声呐条纹特征值为谱图中干涉结构提供了一种简单的量化关系，并且随着发射频率的增大，曲率和强度表现为减小的趋势。通过弹性球壳水下实验获得接收器处的声场干涉条纹，所得的曲率和值与理论分析结果之间有较好的吻合度。但是，本文在理想波导环境下进行研究，未考虑复杂波导环境下主动声呐干涉条纹的生成及变化，下一步将在复杂海洋环境下研究主动声呐干涉条纹的生成及特征表征，并探索不同水体环境对干涉结构的影响以及目标运动轨迹与干涉条纹结构的关系，同时根据干涉条纹结构进行目标跟踪及定位相关研究。