比较大小也可以“小题大做”

刘大伟 李勇霞

(重庆市江津中学校)

纵观近几年的高考,比较大小问题已从单一的知识考查,过渡到多知识融合的综合性考查,求解方法也从常规的作差法和作商法,过渡到借助函数、不等式和导数等知识进行知识和技巧的双重运用.该类型问题综合性很强,旨在考查学生的转化能力、推理能力和计算求解能力等,涉及化归与转化思想,渗透直观想象和数学运算素养等.

1 利用对数函数的单调性实现“小题大做”

点评在利用对数函数的单调性进行试题求解的过程中,往往会涉及对数形式的化简及实数比较大小的常用方法等,同时,要求学生具有敏锐的观察力,找到中间值是求解该题的关键.

点评在判断对数值正负的过程中,有时会用到如下结论:logab的正负由a,b共同决定,若a,b都在区间(0,1)或(1,＋∞)上,则对数值为正,否则为负.

2 借助中间值实现“小题大做”

例3若a＝log23,b＝log34,c＝log45,则a,b,c的大小关系是( ).

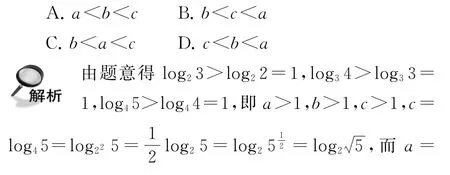
由于y＝xlnx在(1,＋∞)单调递增,故当x∈(1,＋∞)时,h′(x)＜0,即h(x)在(1,＋∞)单调递减,所以h(2)＞h(3)＞h(4),即c＜b＜a,故选D.

3 利用基本不等式实现“小题大做”

例4(2020 年全国Ⅲ卷理12)已知55＜84,134＜85.设a＝log53,b＝log85,c＝log138,则( ).

A.a＜b＜cB.b＜a＜c

C.b＜c＜aD.c＜a＜b

点评由题意可知a,b,c∈(0,1),故

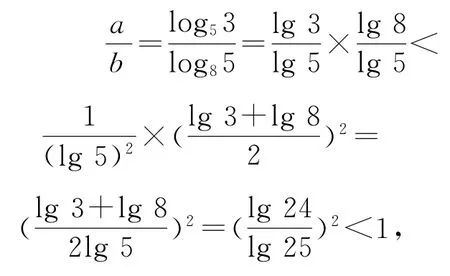
所以a＜b.

综上,a＜b＜c,故选A.

点评该题的求解过程用到对数的换底公式、基本不等式、指数函数单调性等知识,该题在求解过程中,基本不等式的运用是解题的关键,而基本不等式在试题中的主要作用往往涉及最值的求解.一般地,利用不等式(当且仅当x＝y时,等号成立)求最小值;利用不等式(当且仅当x＝y时,等号成立)求最大值.在比较大小过程中,求解对数的运算以及基本不等式的综合试题的关键在于熟练运用运算的技巧以及相关性质.

4 通过构造函数实现“小题大做”

综上,c＜a＜b,故选C.

解析该试题要求学生具备敏锐的观察能力,由c＝－ln0.9＝ln0.9－1＝,可以构造函数h(x)＝ln(1－x)－x,从而探究b,c之间的大小关系,因此,寻求条件中相关数据之间的联系是构造函数的前提.

例7(2022年全国甲卷文12)已知9m＝10,a＝10m－11,b＝8m－9,则( ).

点评首先由条件9m＝10,可得m∈(1,1.5),同时,根据条件a,b的特点,构造函数f(x)＝xm－x－1(x＞1),从而进行常规求导,判断单调性,利用函数的单调性比较a,b的大小.

5 小结

纵观近几年的高考,通过构造函数,实现大小比较,依然成为一种重要方法,关键在于通过对比题干数据,构造恰当函数,通过常规求导,实现数据的大小比较.该类问题综合性很强,旨在考查学生的转化能力、推理能力和计算求解能力等,涉及转化与化归思想,渗透直观想象和数学运算素养等.

总而言之,比较大小类问题往往以指数、对数函数、幂函数的定义、图像和性质为基础,综合不等式、三角函数、导数等相关知识,实现知识的综合运用.此外,该类型试题往往涉及函数与方程思想、特殊与一般思想以及转化与化归思想等,设置巧妙,考查学生的数学抽象、逻辑推理以及数学运算等核心素养.

链接练习

链接练习参考答案

1.A.2.B.3.B.

(完)