3d过渡金属离子在无机化合物中的基态能级及变价趋势理论探索

屈冰雁，王雷

（合肥工业大学 材料科学与工程学院，安徽 合肥 230009）

1 引 言

3d过渡金属（TM,Transition metal）离子的3d轨道对晶格环境非常敏感，这一特性为新型发光材料的设计提供了巨大空间。近年来，3d-TM离子如Mn2+、Fe3+以及Cr4+等，在激光[1]、LEDs[2]以及长余辉[3-4]等多种功能材料中均展示了广阔的应用前景。3d-TM离子激活发光材料掺杂时，其在化合物中的能级位置影响着材料的发光性质，对设计相关发光材料而言，关键点在于3d-TM离子基态在带隙中位置的确定[5]。如图1（a）所示，在宽带隙化合物中，若3d-TM离子的基态在带隙中的位置已确定，则激发态位置可通过Tanabe-Sugano图进行预测；若激发态进入导带，则会发生猝灭。类似地，如基态进入价带，其发光也会发生猝灭[6]。如存在能级位置合适的载流子陷阱中心，则会形成余辉现象。上述过程的示意图如图1（b）所示[3,7]。因此，预先评估离子在化合物中的基态和激发态位置，对相关材料的发光性质设计以及调控具有重要意义。

图1 （a）3d5构型过渡金属离子（如Fe3+或Mn2+）在宽禁带化合物中的电子结构示意图［8］，其中右侧为该构型的Tanabe-Sugano图；（b）过渡金属离子在化合物中可能的猝灭或者余辉（PerL）机理示意图。G表示基态，E表示激发态。Fig.1（a）Schematic electronic structure of transition metal ions with 3d5 configuration（e.g.Fe3+or Mn2+）in wide band compounds［8］with the corresponding Tanabe-Sugano（T-S）diagram.（b）Possible quenching and afterglow mechanisms.G denotes ground state and E denotes excited states.

首先，回顾3d-TM离子基态位置的物理描述方式。通常存在两种描述3d-TM离子在材料中能级的方式。其一为晶体场理论[9]，即Tanabe-Sugano图[10]，可成功揭示3d-TM离子的吸收、激发等组态内跃迁性质。另一种描述是分子轨道理论，侧重于描述3d轨道与配体轨道之间的杂化作用。考虑到晶体的价带是由配体轨道相互作用形成，若以配体轨道为桥梁，理论上可以给出杂化作用后的3d轨道能级在晶体能带中的相对位置，这是晶体场理论所不能提供的。该位置信息可用于解释因3d-TM离子掺杂而产生的电学、光电导和离化等特性。晶体场理论侧重描述电子在离子轨道的局域特性，后者可描述有关电荷与非局域相关的属性，如热/光离化、电荷俘获等变价特性。

与此对应，镧系离子（Ln2+、Ln3+）与TM离子也存在上述两种物理描述，4f-4f以及4f-5d的跃迁可用晶体场理论描述。对于4f轨道的离化或者5d轨道的离化、4f轨道的俘获（从价带至三价Ln3+）等变价行为则可用分子轨道理论描述。在镧系离子激活的发光材料中，根据4f轨道对晶体场不敏感的特性，以及镧系离子的离化（离化能）、俘获（电荷迁移带）等变价特性，Dorenbos对镧系离子能级给出了化学势模型，指出其在一般化合物中折线趋势的变化规律（图2）[11-12]。这与苏锵院士给出的镧系离子价态变化趋势[13-14]（图3）基本一致。该趋势反映镧系离子的变价行为，本质上源自不同离子间的光学电负性差异[13-15]，而光学电负性可以描述离子的电荷迁移属性[16-17]。在大量化合物中，镧系离子的价态变化趋势波动幅度很小。可利用镧系离子掺杂引入不同深度的电子陷阱，为设计相关载流子俘获-释放过程的发光材料提供了理论依据。

图2 镧系离子在YPO4中的能级图［18］。红色折线为Ln2+/3+的价态转变能级（2+价转3+价）；蓝色折线（4f）为Ln3+/4+的价态转变能级（3+价转4+价）。其中的短横线为离子的激发态，嫁接自Dieke Diagram。Fig.2 Energy levels of lanthanide ions in YPO4［18］.The red zig-zag like curve presents Ln2+/3+charge transition levels（from 3+to 2+）.The blue curve（4f）presents the Ln3+/4+charge transition levels（from 3+to 4+）.The short bars represent excited state levels of Ln ions derived from the Dieke-Diagram.

图3 镧系离子变价趋势图［13-14］Fig.3 The charge transition tendency of lanthanide ions［13-14］

值得注意的是，Dorenbos认为图2中红色或蓝色折线可以视为镧系离子2+或3+价的基态位置[19]，并将Ln3+的能级结构图（Dieke Diagram）[20]嫁接在镧系离子的基态位置上[21]，用于估算4f和5d轨道的激发态能级[18]。这种把晶体场和晶体能带结构结合起来的做法为预测镧系离子的发光性能提供了理论支撑[21]。

那么，对于3d-TM激活发光材料是否存在类似的趋势？为回答该问题，我们从近70年文献的大量光谱数据中整理了相关TM离子的信息，并结合第一性原理计算研究了3d-TM离子在化合物中的能级规律[5,8]。在这里，所涉及的大量文献不再一一列出，仅提供部分关键文献供参考。

2 3d-TM离子基态测算的物理依据和方法

在激发光谱中，与3d-TMn+离子相关的激发峰主要有两类，一类是电荷迁移带（Charge transfer band，CT），是指配体轨道上的电子激发到TMn+的未占据轨道。另一类为3d电子组态内跃迁，可给出TMn+的基态和各激发态之间的能量差，即Tanabe-Sugano图。通常，材料的价带主要由阴离子轨道形成，因此，CT能量即为TMn+最低激发态能级与价带之间的能量差，可反映TM（n-1）+（激发后，TM变为（n-1）+价）束缚电子能力的大小。所以，可称之为“相对于价带的电子束缚能HRBE（Host referred binding energy）”，即以价带为能量参考零点时的电子束缚能。通常，将HRBE（TMn+/（n-1）+）视为TM（n-1）+基态能级位置，这与Dorenbos在处理镧系离子时的做法一致。于是，HRBE、CT和TM基态能量满足如下关系：

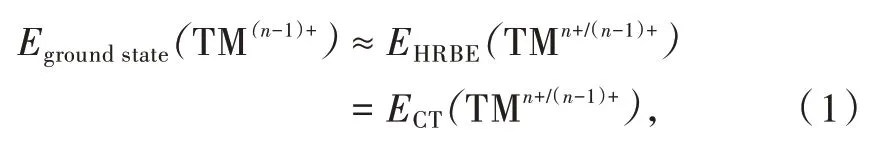
为便于比较不同基质中3d-TM离子的电子束缚能，需选择一个共同的能量参考零点。真空能级是一个很好的选择，对应的能级称为真空电子束缚能VRBE（Vacuum referred binding energy）。HRBE和VRBE满足方程：

其中，EVRBE（VB）为以真空能级为能量参考零点时价带的能量。

在理论计算方面，3d-TM离子的光学转变能级（Optical transition level,OTL）表示价带顶（Valence bands maximum，VBM）的电子跃迁到3d-TM离子最低未占据缺陷能级所需的能量，这与CT过程在物理上几乎一致，仅有的不同点是：在OTL中，电子是从价带顶跃迁到3d-TM离子的最低未占据能级；而在CT中，电子是从价带开始跃迁的。因此，OTL低估CT，但是OTL有可能准确提供同一个化合物中不同3d-TM离子的CT变化趋势。从TMn+转变到TM（n-1）+的OTL定义为：

其中，E（TMn+）和EVBM分别为TMn+掺杂时系统的能量和基质价带顶的能量。所有这些能量都是采用基于密度泛函理论的VASP软件包计算获得。电子波函数采用截断能为400 eV的平面波基组描述，交换关联势采用广义梯度近似（GGA）下的PBE泛函。原子受力的收敛条件为0.1 eV/nm。

3 3d-TM离子在四面体和八面体晶体场中的基态能级位置

3d轨道处于3d-TM离子的最外层，对晶体场较为敏感，可根据晶体场类型将3d-TM离子在发光材料中的占位情况进行分类以评估3d-TM离子对电子的束缚规律。本文主要介绍四配位四面体晶体场和六配位八面体晶体场。在八面体环境下，OTLεf（TM3+/2+）、εf（TM4+/3+）和3d-TM离子的CT的规律如图4所示。从总体来看，采用GGA-PBE计算的εf（TM3+/2+）可以再现ECT（TM3+/2+）的变化趋势，表明当已知一个离子在某一化合物中的CT值时，可以通过理论计算估计其他9个相同价态离子的CT能量。前面提到，CT值决定了3d-TM离子在化合物中的基态位置，采用该方法也可估计3d-TM离子的基态相对价带位置。采用类似的办法可以获得OTLεf（TM4+/3+）的变化趋势。该趋势与OTLεf（TM3+/2+）非常相似，这是由于它们有着相同的电子组态。连接这些OTL或CT数据点，可以得到两条OTL折线。根据公式（1）和（2），可以得到这些离子的VRBE折线，如图4右边纵坐标所示。

随着原子序数的增大，3d原子的轨道能级总体呈降低趋势[22-23]。3d-TM离子在基质中引入的缺陷能级也存在类似趋势（如图4所示），仅有εf（Cr3+/2+）比εf（V3+/2+）高了约1.2 eV。这是因为，α-Al2O3中，V3+为d2电子构型，在CT过程中来自价带的电子应跃迁到自旋向上的三重态上。Cr3+为d3电子构型，而Cr3+在带隙中引入的自旋向上的三重态是满占据的，CT过程中来自价带的电子只能占据能量更高的自旋向上二重态或者自旋向下的三重态。很明显，这需要付出更多的能量（晶体场劈裂能或成对能，Pairing energy），所以，εf（Cr3+/2+）比εf（V3+/2+）要高。

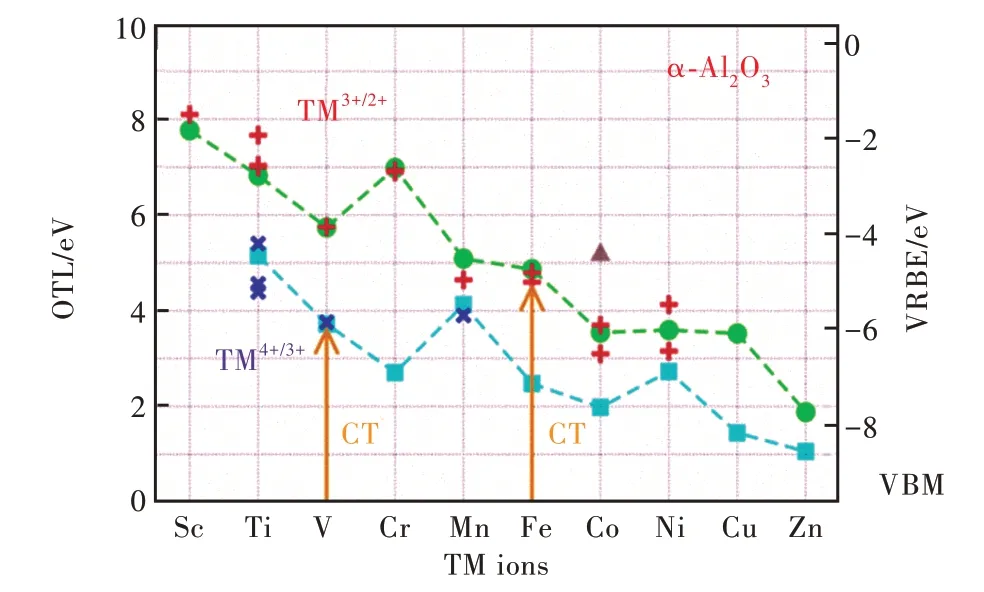
图4 3d-TM离子在α-Al2O3中（八面体环境）的电荷迁移带（CT）和平移后的光学转变能级（OTL）［5］。其中，OTLεf（TM3+/2+）和εf（TM4+/3+）分别采用符号“●”和“■”表示，实验CT能量ECT（TM3+/2+）和ECT（TM4+/3+）采用符号“+”和“×”表示，“▲”表示低自旋态时的εf（Co3+/2+），箭头表示CT过程。Fig.4 The charge transfer bands（CT）and the shifted optical transition levels（OTL）of 3d transition metal ions inα-Al2O3（in octahedral sites）［5］.Here，OTLεf（TM3+/2+）andεf（TM4+/3+）are presented with“●”and“■”while the CT data of ECT（TM3+/2+）and ECT（TM4+/3+）are denoted with“+”and“×”respectively.The low spin state ofεf（Co3+/2+）is denoted as“▲”.The arrows present the CT processes.

除了八面体晶体场环境，3d-TM离子在四面体晶体场中的OTL变化趋势如图5所示，所涵盖的化合物包括铝酸盐、硅酸盐、氮化物和氯化物等。从图5可以看出，3d-TM离子在上述化合物中的OTL变化趋势几乎一致，意味着它们的基态在四面体环境下遵循着一个共同的规律，即从Sc至Zn，离子之间基态的相对位置在四面体环境下几乎不会发生显著变化。

图5 四面体环境中3d-TM离子的OTL趋势图。实线和点划线分别表示εf（TM3+/2+）和εf（TM4+/3+）的OTL［8］；实心点和空心点分别表示精确数据和低估的数据。其中YAG表示Y3Al5O12。Fig.5 The trends of OTL of 3d-TM ions in tetrahedral crystal field［8］.The solid symbols present the accurate data and the open symbols present the underestimated data.YAG is Y3Al5O12.

为了便于评估四面体环境下离子在化合物中的基态位置，我们从图5提取出3d-TM离子的OTL变化趋势，也即是VRBE变化趋势，并与实验结果对比，展示在图6（a）中。将八面体和四面体中3d-TM离子的VRBE结果对比显示于图6（b）。二者有着较大的不同，这表明3d轨道在这两种晶体场中截然不同的劈裂方式不但导致激发态不同，而且其基态位置也会受到影响。

图6 （a）3d-TM离子在四面体化合物中的VRBE趋势［5，8］，其中符号“●”和“■”分别表示计算值，符号“+”和“×”表示实验值；（b）3d-TM离子在四面体和八面体环境下的VRBE，或3d-TM离子的变价趋势图。Fig.6（a）The VRBE trend of 3d-TM ions in tetrahedral sites of inorganic compounds［8］.“●”and“■”represent the calculated results，while“+”and“×”denote the experimental ones.（b）The comparison of the VRBE for 3d ions in tetrahedral sites and octahedral sites，or the charge transition tendency of TM ions in both sites.

4 讨 论

4.1 3d-TM离子在化合物中的缺陷本质

图7为Fe4+掺杂的Y3Al5O12电子结构及态密度。从图7中可以看出，带隙中出现了一些缺陷能级，这些能级的电荷密度图表明它们是由Fe的3d轨道和与Fe配位的O离子轨道形成的反键态。其中Fe的3d轨道贡献较大，表明这些轨道主要体现3d轨道的性质。因此，在特定晶体场类型下，3d轨道的缺陷能级相对固定，这一点与镧系离子类似。其他3d-TM离子的计算结果也支持这一结论。

图7 Fe4+掺杂的YAG电子结构及态密度［8］，右图为两个缺陷能级的电荷密度等值面，其中Fe和O离子分别由大球和小球表示。费米能级为0 eV。Fig.7 Computed electronic band dispersion and DOS of Fe4+doped YAG［8］.The iso-surfaces of the charge density of two defect levels are shown on the right hand.The Fe and O ions are represented by the large and small balls.The Fermi level is set to 0 eV.

同时，缺陷能级既然为3d-TM离子的反键轨道构成，其位置也应受到配体轨道影响，因此化合物的阴离子轨道也会影响这些能级位置。为印证上述论断，基质的价带VRBE与Cr3+/2+、Fe3+/2+以及Mn4+/3+在对应材料中的VRBE进行对比分析，发现两者之间近乎呈线性关系，且不同离子拟合获得的斜率不同（图8（a））。这是因为化合物的价带主要是由配体轨道构成，而配体轨道也在3d轨道引入的缺陷能级中有少量贡献。当配体轨道能量上升时，价带和3d缺陷能级都随之升高，因此，3d-TM离子的基态VRBE随着价带升高。同理，在四面体中，也可以观察到相同的规律（EVRBE（Fe3+/2+））（图8（b））。采用该量化关系，可以从3d-TM离子的VRBE计算出化合物的价带能量，反之，也可从价带能量计算出3d-TM离子的VRBE，其计算精度为±0.23 eV。结果表明，采用本方法可以非常精确地估计TM离子的基态位置。根据这个关系，可以在不经过繁琐计算的情况下估计3d-TM离子的基态能级，结合Tanabe-Sugano图，可以预测3d-TM离子在化合物中的发光性质、电学性质、载流子俘获特性等，也可以结合基质本身的性质对离子的价态进行调控。

图8 （a）八面体环境下Cr3+/2+、Fe3+/2+以及Mn4+/3+的VRBE与基质价带关系［5，8］；（b）四面体环境下Fe3+/2+的VRBE与基质价带关系［8］。Fig.8（a）The VRBE of Cr3+/2+，Fe3+/2+and Mn4+/3+as a function of valence band for octahedral sites［5］.（b）The VRBE of Fe3+/2+as a function of valence band for tetrahedral sites［8］.

4.2 用分子轨道理论评估3d-TM离子能级的近似方法

既然3d-TM离子在化合物中的基态可以预测，在材料晶体场强度不清楚的情况下，是否可以采用分子轨道理论评估3d-TM离子能级？为阐述该问题，图9给出了Mn4+在YAG的电子结构。当3d-TM离子掺入材料后，将会在材料的带隙中形成一些缺陷能级，3d电子在这些缺陷能级上的不同占据方式就构成了3d-TM离子不同的电子组态，其中能量最低的占据方式（电子组态）对应的能级就是基态，其余的能级为激发态。电子在这些能级上的不同占据方式也会造成这些缺陷能级位置的变化，虽然第一性原理计算得到的是基态的缺陷能级，但可以在此基础上定性地讨论电子的激发和发射过程。如图9所示，根据晶体场理论，具有3d3电子构型的Mn4+离子受到八面体环境（YAG）中阴离子的库仑作用后，分裂成三重态t*和双重态e*两种能级位置[6]。激发前，电子满占据自旋向上的三重态，对应着基态4A2，当激发时，电子从该能级激发到自旋向上的双重态，对应着4T2或4T1（这两个状态取决于3d电子在上述轨道上的占据方式）；在弛豫和发射时，由于自旋向下的三重态能量比自旋向上的双重态低，所以自旋向上的三重态将能量弛豫到自旋向下的三重态上，即自旋发生反转，该过程对应着4T2或4T1到2Eg的转变。最后，电子从自旋向下的三重态跃迁回自旋向上的三重态，即自旋再次翻转，并伴随着光发射。

图9 Mn4+的激发发射过程在能带结构（Y3Al5O12）中的描述［6］。（左）3d轨道在八面体晶体中劈裂为能量较高的两重简并态（Doublet）和能量较低的三重简并态（Triplet），Spinup和Spindown表示不同的自旋；（右）Y3Al5O12∶Mn4+的能带和态密度。Fig.9 The schematic graphic of the excitation-emission process of Mn4+in Y3Al5O12.The left panel shows the 3d orbitals in an octahedral crystal field split into the doublet states and the triplet states of both spin states.The right panel is the electronic structure and density of states of Mn4+doped Y3Al5O12.

5 结论与展望

本文介绍了3d-TM离子（从Sc至Zn）作为激活剂离子在一般无机化合物中的缺陷能级的起源及其在不同化合物中的演化规律。在特定构型下，3d-TM离子的基态能级位置会随着价带能量呈线性增加。根据这种线性关系，可以将3d-TM离子在化合物中缺陷能级位置的预测精度提升到±0.23 eV。在此基础上，结合Tanabe-Sugano图，可精确预测离子的猝灭行为、光谱形状、由掺杂形成的陷阱能级等。根据3d-TM离子的基态位置演化规律以及上述预测方法，可为3d-TM离子激活发光材料的智能设计提供更多评估手段。

值得注意的是，本文给出的3d-TM离子基态的演化趋势也可描述3d-TM离子在化合物中的变价趋势，且同一种价态离子趋势图在同一种对称格位下几乎不发生很大变化。因此，由2+或者3+价态的任一TM离子的基态能级位置可获得其他九种对应价态离子的基态位置。在电荷迁移带光谱的归属上，同样具有重要参考价值。同时，由3d-TM离子的变价趋势图，通过调节化合物基质的费米能级，可智能调节过渡金属离子的价态等[24]。随着实验光谱数据的增加，有理由相信，上述设计方法的精度会进一步提高，可为新型发光材料的设计提供更加有力的支撑。

感谢荷兰代尔夫特理工大学Dorenbos教授和罗宏德博士、合肥工业大学陈雷教授、周如龙教授和蒋阳教授、中国科学技术大学潘必才教授和夏上达教授、兰州大学王育华教授的有益讨论和支持等。

本文专家审稿意见及作者回复内容的下载地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220222.