基于快速独立分量分析与改进随机子空间算法相结合的次同步振荡模态辨识

王雨虹，宋志超，孟宪敬，孙少华

（1.辽宁工程技术大学电气与控制工程学院，辽宁 葫芦岛 125105；2.开滦集团，河北 唐山 063000；3.国网宁德供电公司，福建 宁德 352100）

0 引言

近年来，我国风力发电总装机容量不断增加，为了适应能源赋存与消耗逆向分布的格局，大功率高电压直流输电在风电系统中得到了广泛应用。输电线路中串联了大量的电容补偿器，致使次同步振荡（subsynchronous oscillation，SSO）问题日益突出［1-2］。输电系统次同步振荡的发生不仅会造成降低系统传输功率，严重时还可能导致风机脱网、发电机轴系断裂的事故，对电力系统的稳定运行有着严重的威胁。为此，需要快速、准确地辨识出次同步振荡的各个模态，以便对次同步振荡进行监测、预警和抑制。

传统的次同步振荡分析方法多以系统整体模型为基础，如频率扫描法［3］、特征结构分析法［4-6］、复转矩系数分析法［7］等。然而，随着电力系统规模的扩大，整体结构复杂度的增加，难以建立完善的电力系统模型，使得稳定性分析结果存在较大的误差。近年来，广域量测系统的成熟发展，为基于实测数据的次同步振荡在线辨识提供了充足的条件［8-10］。文献［11］采用小波去噪和Prony算法结合的辨识方法，虽能解决Prony算法抗噪性弱的问题，但在去噪中过于依赖阈值的选取，易产生虚假模态或模态遗漏现象。文献［12］在次同步振荡辨识中采用总体最小二乘-旋转不变算法，该方法在辨识速度和精度上具有优势，但在强噪声环境下辨识结果存在较大误差。为此文献［13］引入Hankel矩阵来改进总体最小二乘-旋转不变算法，降低噪声干扰，但该算法存在模态阶数定阶难的问题。文献［14］采用的递推随机子空间辨识方法虽能提高辨识速度，但随机子空间算法的应用必须具备模态阶数确定的前提。文献［15］采用稳定图法来对随机子空间算法定阶，但由噪声引起的稳定极点并非真实情况的稳定点，稳定图无法剔除噪声模态。

由于电网中存在大量电力电子设备，造成实测信号中包含强干扰噪声，而噪声的干扰会让辨识方法出现系统阶数难以确定的问题。当系统模态阶数过高会包含噪声子空间存在虚假模态，模态阶数过低会遗漏信号模态。因此，对实测信号有效地降噪进而准确地确定系统模态阶数在次同步振荡辨识中至关重要。为此，本文提出一种将快速独立分量分析技术（fast independent component analysis，FastICA）和基于精确模态定阶改进随机子空间算法（stochastic subspace identification，SSI）相结合的方法。首先，用快速独立分量分析技术对实测信号进行噪声和原信号的分离预处理［16］，将处理后的信号输入随机子空间算法，针对随机子空间算法难以准确估计模态阶数的问题［17］，用精确模态定阶的方法予以改进，避免出现虚假模态和模态遗漏的现象，确定信号中的主要模态，进而辨识出各个模态参数。由风电场仿真算例和实际电网数据验证了该方法在强噪声环境下能够有效地进行去噪预处理，并且准确地计算出模态阶数，快速辨识出振荡的主要模态参数。

1 快速独立分量分析技术与精确模态定阶改进随机子空间算法的基本原理

1.1 快速独立分量分析技术

快速独立分量分析技术是一种快速寻优迭代算法，在信号的盲源分离和特征提取方面应用广泛。广域量测系统从电网采集的信号数据都会包含由快速励磁、负荷功率随机变化产生的干扰噪声。对于这种混杂信号，快速独立分量分析算法能够有效地将噪源信号分离，起到降噪的作用［18］。

次同步振荡采样信号由Y表示，线性模型为：

式中：A为混合矩阵；S为独立源向量。

快速独立分量分析技术的任务是在A和S未知的情况下构建解混矩阵B，将原信号从采样信号中比较完善地分离出来。表达式如下：

若要使͂最大程度逼近S，只需要满足解混矩阵B最佳近似于A-1。

在随机变量中，用负熵来度量非高斯性［19］。负熵表达式近似为：

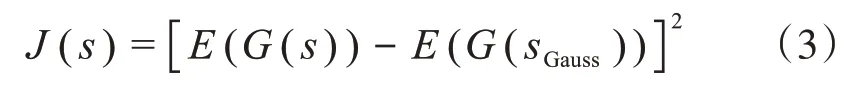
式中：E(⋅)为均值函数；G(⋅)为非线性函数；s为独立源信号；sGauss为s的高斯分布向量。

依据极大化非高斯性原理，通过负熵使目标函数最大化，得到最佳估计解混矩阵，对源信号进行有效地分离［20］。以负熵最大作为搜寻方向，其迭代公式为：

式中B*为中间矩阵。

标准化处理得到解混矩阵，进而从采样信号中分离出原信号。

1.2 基于精确模态定阶改进的随机子空间算法

1.2.1 随机子空间算法

将由快速独立分量分析技术分离而来的原信号y k构造Hankel矩阵。

式中：i=2n，n为系统阶数；j为量测量采样数。令Y-f=Y i+1|2i-1和Y+p=Y0|i。

使用Hankel子矩阵确定投影矩阵P i。

对投影矩阵P i进行奇异值分解。

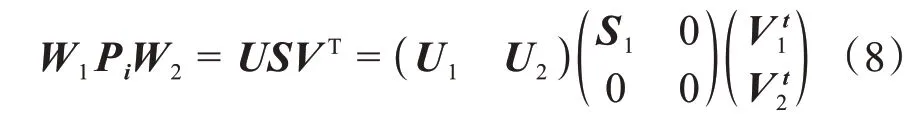
形成扩展可观测矩阵Γi。

计算卡尔曼滤波状态序列。

确定系统状态矩阵并且对其进行特征值分解。

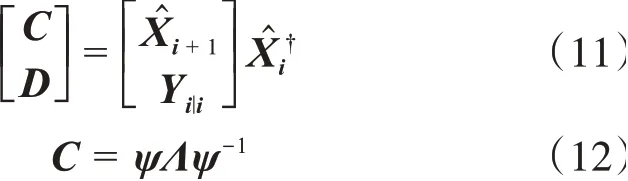
式中：C为系统状态矩阵；Λ=diag(λi)∈Rn×n，i=1，2，…，n；λi、ψ分别为离散系统特征值和特征向量矩阵。

根据系统连续特征值ηi计算次同步振荡的频率fk、阻尼比ξi和衰减因子ςi。

式中：Δt为采样时间间隔；ηi*和ηi互为共轭；|·|表示模。

1.2.2 精确模态定阶法

随机子空间算法虽对诸多振荡模态具有很好的识别效果，但是在含噪信号中对模态阶数的选取要求较高，难以识别出信号的主要模态［21-22］，所以精确地估计系统模态阶数是该方法的关键［23］。文献［24］中直接用奇异值分解确定系统阶数，但在含噪信号中奇异值并不能很好地表示各个模态的能量分布，会有过多的虚假模态，使辨识结果存在较大误差。文献［25］提出用奇异熵来确定系统阶数，这种方法过度依赖阈值的选取，在信噪比不同的信号中，阈值选取困难，在强噪声干扰环境下，会遗漏信号模态。

本文将精确模态定阶的方法应用到随机子空间算法中，对其定阶难的问题予以改进。在次同步振荡信号辨识中，特征值的大小分布能够代表信号的能量分布，根据特征值的大小和分布规律，设定两个判据，对模型阶数精确定阶。

1）特征值的相对差值最大。

由系统状态矩阵分解而来的特征值能够显著地代表次同步振荡信号的功率谱密度，因此在信号和噪声子空间的接合点处会有显著的变化。按照其能量大小的分布，较大的特征值表示包含主要模态的信号，即信号子空间；较小的特征值表示噪声信号，即噪声子空间。按降序排列的特征值从最大值逐渐减小，直到λi骤然降低，随后λi+1保持很小的能量且缓慢地降低。说明λi是信号子空间和噪声子空间的界点，即i为系统模态的阶数。定义连续特征值λi的相对差值（relative difference，RD）来确定信号子空间和噪声子空间的界点。

当相对差值取到最大值时，i即为系统的实际模态阶数。此时，已经能够解决由噪声带来的虚假模态问题，准确地确定系统模态阶数。然而当信号中出现一个或多个主要模态，并且其能量远大于其他振荡模态时，系统可能会将取得最大相对差值对应的阶数确定为模态阶数。实际阶数对应的相对差值并非最大相对差值，因此出现模态遗漏现象。为避免这种现象的发生，用第二判据进行验证。

2）相对差值对应的特征值属于信号子空间

在第一判据中选取多个较大相对差值对应的阶数作为候选阶数，候选阶数所对应的特征值由大到小依次用式（18）进行验证。

式中：l为系统模态的候选阶数；λi为相应的特征值；α为灵敏因子，取值在2—4。本文灵敏因子取值为4，因较大的灵敏因子对应较高的灵敏度，即使信号中模态分量较小也能够被检测出，做到不遗漏模态。

精确模态定阶法以特征值的相对差值最大作为第一判据，避免系统模态阶数过高，产生虚假模态；以相对差值对应的特征值属于信号子空间作为第二判据，避免系统模态阶数过低，出现模态遗漏现象。上述两个判据能够很好地解决在噪声环境中模态定阶难和阈值难选取的问题，极大地提高了定阶的准确性。

2 基于快速独立分量分析技术和改进随机子空间算法对振荡模态参数的辨识

2.1 算法流程

以广域量测信号作为采样信号，对包含噪声和原信号的采样信号用快速独立分量分析技术进行噪源信号的分离，减少强噪声的干扰；采样信号经过预处理后，依然存在干扰噪声，为了提高辨识精度，用精确模态定阶法改进随机子空间算法，来精确计算系统模态阶数，避免出现虚假模态和模态遗漏的现象，确定主要模态，准确地辨识各个模态参数。具体步骤如图1所示。

图1 方法流程图Fig.1 Method flow chart

步骤1：以广域量测得到的采样信号输入信号，并对其进行零均值化和白化处理。

步骤2：确定需要估计分量的个数，设定迭代次数。

步骤3：构建解混矩阵，在负熵最大的方向进行迭代计算。

步骤4：确定收敛后的解混矩阵，对采样信号分离出噪声信号和原信号。

步骤5：由含微弱噪声的原信号构造Hankel矩阵，并且由观测矩阵确定系统的状态矩阵，进行特征值分解。

步骤6：为了准确地得出系统模态阶数，用精确模态定阶法改进随机子空间算法。对特征值求取相对差值，以此来确定信号子空间和噪声子空间临界点。

步骤7：选取系统模态的候选阶数，并用式（18）来判别所选阶数是否对应主要信号子空间。

步骤8：确定模态阶数，进而得出各个振荡模式的特征参数。

2.2 评价标准

为比较辨识后的重构信号和原信号的拟合程度，引入评价标准—拟合精度（accuracy of fitting index，AOF）。

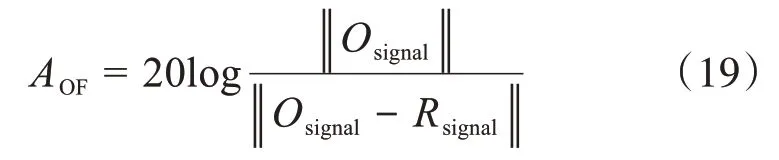
式中：Osignal为原信号；Rsignal为重构信号；‖‖·表示二范数；AOF单位为dB。正常而言，当AOF≥10时就满足拟合精度的要求。

3 算例分析

3.1 理想算例

构造理想信号x(t)：

其中：

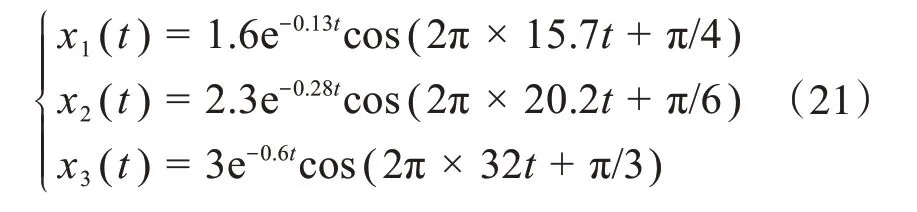
该信号的主要参数如表1所示。

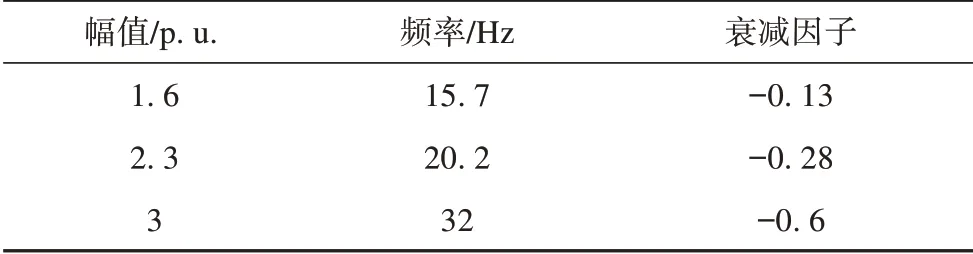
表1 理想信号参数(模型阶数为3)Tab.1 Idealsignal parameters with a modalorder of three

为了验证本文方法在强噪声环境下的去噪效果，在理想信号式（21）中加入高斯白噪声，图2为理想信号和加噪信号。利用快速独立分量分析技术对信号进行预处理，图3为分离后的信号和理想信号，图4为分离后的噪声信号。通过观察图3中两条曲线，可以很明显地看出原信号能被较好地分离出来，信噪比也由原来的5 dB提高到了19.574 1 dB，说明快速独立分量分析技术能够对含噪信号进行有效的预处理。

图2 理想信号和加噪信号Fig.2 Idealand noise-added signals

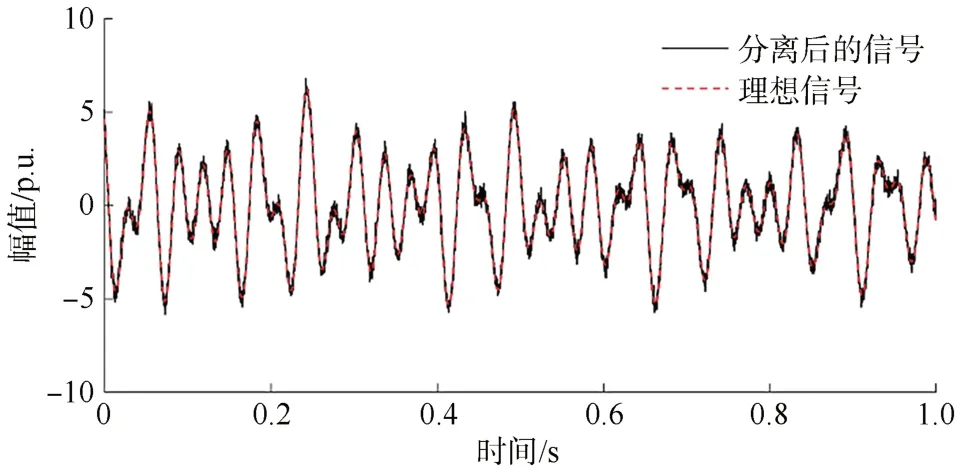
图3 分离后的信号和理想信号Fig.3 Separated signaland idealsignal

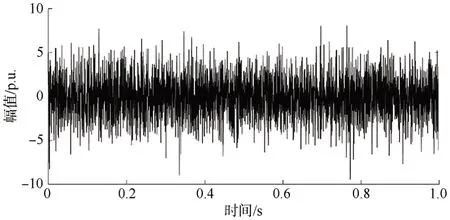
图4 噪声信号Fig.4 Noise signal

分别采用本文方法、基于集合经验模态分解（ensemble empirical mode decomposition，EEMD）［26］的矩阵束算法（matrix pencil，MP）和特征值系统实现算法（eigenvalue system realization algorithm，ERA），对添加了5 dB、15 dB高斯白噪声的理想信号算例进行辨识，结果如表2所示。

表2 辨识方法对比Tab.2 Comparison of identification methods

由表2可以看出，在模型定阶中，基于集合经验模态分解的矩阵束算法（EEMD-MP）和ERA算法确定的模型阶数均存在过高现象，在信噪比（signal noise ratio，SNR）为5 dB的信号中，EEMD-MP法出现了虚假模态的现象。ERA算法虽然能够辨识出各个模态特征，但模型阶数估算过高导致辨识精度上误差较大。相较而言本文方法在含噪信号中不仅能够有效准确地确定模态阶数，更精确地辨识出各个模态的参数，对各个振荡模态的频率、衰减因子辨识精度更高。说明本文方法能够有效地去除噪声的干扰，并且准确地计算模态阶数，进而在误差更小的情况下辨识出信号中各个模态的频率和衰减系数。

为了进一步验证本文方法在去噪和辨识精度方面有更好的优越性，作出加噪信号经本文方法、EEMD-MP算法和ERA算法辨识后的拟合曲线，并计算拟合精度，其结果如图5、表3所示。可以看出，与其他两种方法相比，加噪后的理想信号经本文方法辨识后与原始信号拟合精度更高，从而使得拟合曲线和原信号更吻合。

表3 拟合精度Tab.3 Fitting accuracy

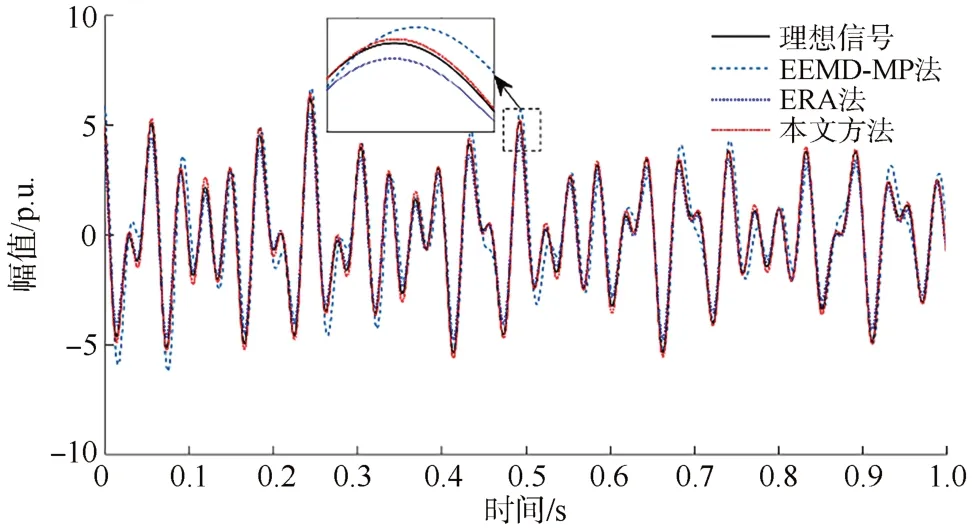
图5 拟合曲线Fig.5 Fitting curves

表4为用本文方法和随机子空间算法对不同的SNR值下的信号进行模型阶数估计和完成时间的对比。相较于随机子空间法，本文方法对模态阶数估计更为精确，并且具有更快的辨识速度。

表4 模态阶数和完成时间Tab.4 Mode order and completion time

3.2 风电场标准模型

为进一步验证本文方法在次同步振荡参数辨识时的可行性，在PSCAD平台搭建双馈风电场标准模型进行仿真分析，图6为系统结构图。模型有5个扭振频率：15.70、20.22、25.55、32.30、47.45 Hz。

图6 双馈风电场标准模型结构图Fig.6 Structure diagram of standard modelof doubly fed wind farm

仿真条件：仿真时间设为2 s，在t=1.5 s时，施加扰动使其发生三相短路故障，受到扰动的系统其变流器与电网侧发生动态交互作用，引起次同步振荡。取系统电压作为分析信号，如图7所示。

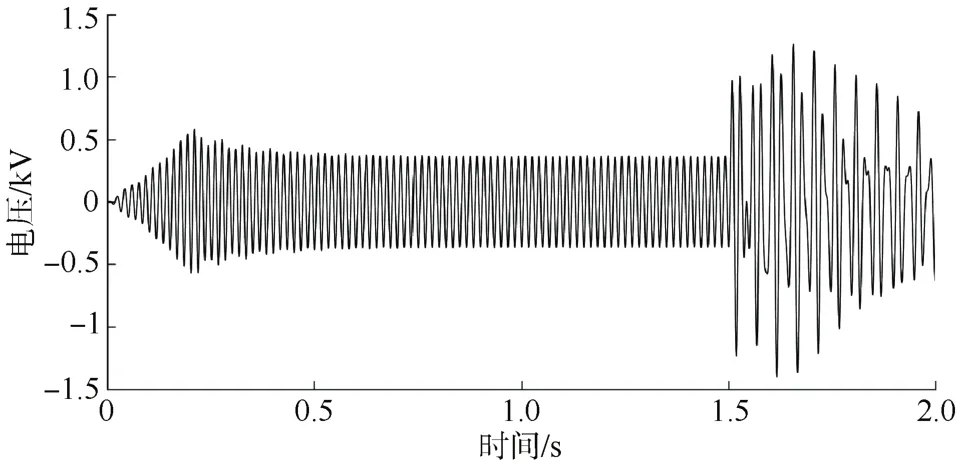
图7 系统电压Fig.7 System voltage

为贴近现场的实际情况，在t=1.5～2 s时段的电压信号中加入SNR值为5 dB的白噪声，加噪后的信号和原信号如图8所示。图9为含噪信号经快速独立分量分析算法预处理后得到的分离信号和原信号，可以看出该算法几乎完整地将原信号分离出来，SNR值也由原来的5 dB提高到了16.734 9 dB，说明确实起到了较好的降噪作用。

图8 加噪信号和局部原信号Fig.8 Noisy signal and localoriginalsignal

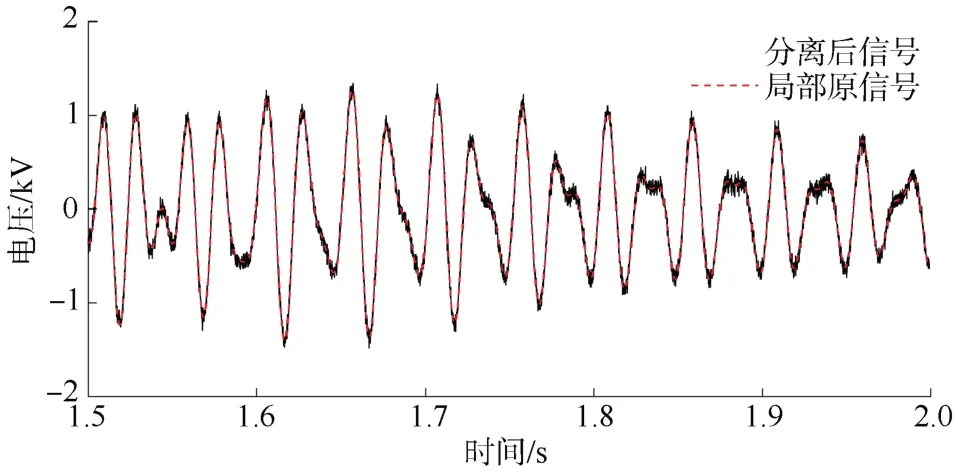
图9 分离后的信号和原信号Fig.9 Separated signaland idealsignal

对加噪信号分别采用改进MP算法［27］、改进Prony算法［28］和本文方法进行辨识，其结果如表5所示。由表5可知，改进的Prony算法由于受到噪声影响，没有辨识出20.22 Hz振荡模式，并且在别的振荡模式上所提方法在辨识精度上更优越。而改进的矩阵束算法，因为对系统模态阶数定阶偏高，致使辨识结果中出现了虚假模态。相较之下，所提方法在对模态阶数准确定阶的前提下，能够准确地辨识出系统的各个模态，并且拟合精度更高。

表5 辨识结果对比Tab.5 Comparison of identification results

3.3 实际工程算例

实际算例采用新疆某风电场输电系统，其网络构架图如图10所示。取ZGH、XH和TD 3个相邻风电场实测数据来验证。其中图11为ZGH、XH和TD 3风电场实测电流信号和局部放大图。由图11可以看出，实测数据在10 s时开始发生持续振荡，并且在15.8 s时振荡幅度增大。

图10 风电场架构图Fig.10 Wind farm architecture diagram

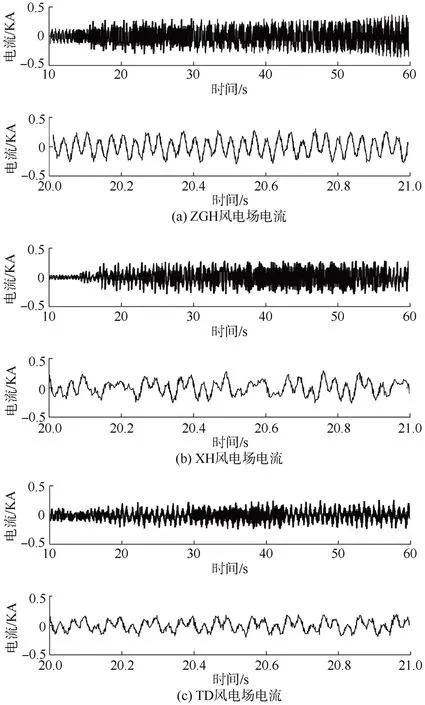
图11 ZGH、XH、TD风电场电流Fig.11 Current of ZGH,XH and TD wind farms

将3个风电场电流作为分析信号，然后用本文方法对采样信号进行降噪处理和辨识，选取20—21 s局部放大，如图12所示。由图12很明显可以看出，与实测信号相比，经快速独立分量分析技术去噪后的信号其由噪声造成的毛刺状得到显著的减少，降噪后的波形完整光滑，说明对于实测信号该方法也能起到很好的降噪作用。

图12 ZGH、XH、TD风电场局部电流分离信号和实际信号Fig.12 Localcurrent separation signaland actualsignalof ZGH,XH and TD wind farms

将去噪后的信号输入改进的随机子空间算法中进行模态参数的辨识，结果如表6所示。由表6辨识结果可知，文中所用方法能够辨识出3个风电场中存在6个次同步振荡模态，且衰减系数均为正值，说明电流呈现振荡发散状态，与电场实测数据波形相符。由此可得，本文方法能够快速有效地辨识出该风电场的各个振荡模式及其参数。

表6 辨识结果Tab.6 Identification results

4 结论

针对次同步振荡在线辨识中在强噪声环境下系统模态定阶难的问题，提出一种快速独立分量分析技术和精确模态定阶改进随机子空间相结合的次同步振荡辨识方法。首先，用快速独立分量分析技术对采样信号进行预处理，分离出原信号，然后用精确模态定阶的思想来计算信号的模态阶数，以此来确定信号的主要模态，最后快速准确地辨识出信号的模态参数，判断是否发生次同步振荡现象。

通过仿真算例和实际工程算例进行验证，结果表明对于强噪声环境里的信号，该方法不仅能够有效地分离出原信号，还能够剔除虚假信号做到不遗漏重要的模态，提高了抗噪性、辨识速度和辨识精度，并且能够准确地辨识出实际输电系统的各个振荡模式，为次同步振荡的抑制措施奠定了基础。