基于下垂控制的柔直变流器孤岛-并网控制模式切换方法

邹常跃，陈俊，魏伟，杨双飞，侯婷，冯俊杰

（直流输电技术国家重点实验室（南方电网科学研究院），广州 510663）

0 引言

近年来国内柔性直流（以下简称为柔直）输电技术快速发展［1］，南澳柔直工程是国内首个多端柔性直流输电示范工程，将风电场接入交流配电网，直流侧电压±160 kV，容量200 MVA。此后国内相继建成了云南背靠背柔直工程、渝鄂背靠背工程、舟山多端柔直、张北工程等［2-3］，其电压等级和容量不断提高，近期建设中的乌东德三端混合直流工程，接入主干网，电压等级±800 kV，将柔直技术应用于特高压领域，控制技术和设备可靠性都在不断提升。基于电网电压定向的矢量控制策略和定电压、定功率等运行方式已在实际工程中广泛应用［4-7］，技术相对成熟。

柔直变流器既可以并网运行也能够单独实现孤岛供电或风电场等新能源接入，如南澳多端柔直工程中，共3个柔直换流站，其中岛上金牛站和青奥站采用交流和直流线路并联方式接入岸上塑城换流站。此外柔直接入电力系统后，在并联交流线路故障期间柔直也可以以孤岛方式运行，持续对负荷供电，待交流系统恢复后再切换为并网运行。孤岛状态下通常为定交流电压幅值和频率（定VF）控制方式，而在并网条件下采用定有功和无功功率（定PQ）方式。两类控制模式转换逻辑相对复杂。对此，文献［8］提出一种变流器孤岛控制结构，在传统基于锁相环的矢量控制结构基础上，附加频率外环和无功外环，使得频率-有功功率和无功功率-电压呈现类似下垂的外特性，改善并网和孤岛间切换过程的稳定性。文献［9］基于一种虚拟同步机外环串联电流内环的控制结构，提出孤岛和并网控制模式的平滑切换方法，在电网频率异常时断开VSG外环，切换为定电流控制模式，电网频率恢复后电流内环给定值恢复为外环输出。文献［10］同样基于虚拟同步发电机（virtual syschronous generator，VSG）设计变流器外环控制结构，仅需要在并网前，调节变流器输出电压幅值和相位与电网同步。文献［11］基于无功功率-电压、有功功率-频率的下垂控制设计变流器控制结构，针对离并网转换提出一种新的交流电压幅值和相位同步方法，避免预同步环节对下垂控制环节的影响。文献［12］针对孤岛和并网分别设计VSG结构和基于常规矢量控制的P Q控制模式，通过控制模式的切换实现两种工况的稳定运行和稳态功率的准确跟踪。文献［13-14］模拟交流系统同步发电机并网过程，在变流器控制结构中附加虚拟阻抗环节，控制流过虚拟阻抗的虚拟交流电流为0实现变流器输出电压与交流电网的自同步。文献［15］基于下垂控制设计变流器孤岛和并网控制器，使二者结构相似，便于孤岛和并网的平滑切换。文献［16］基于抗积分饱和控制器设计方法提出变流器功率环控制结构，当交流电压幅值超过设定上下限值后，在常规PI调节器的积分环节和输出调制信号中加入补偿分量，改变并网时PI调节器无差调节特性，能够在孤岛状态下稳定运行，实现外环控制器特性的自动切换。文献［17］总结了单变流器和多变流器并联时控制模式切换方法，包括下垂控制及其二次调节策略，以及和电网同步方法等。文献［18］考虑多变流器并联运行，孤岛和并网模式下均采用下垂控制，孤岛情况下输出交流电压频率可能偏离额定值，对此提出下垂控制中的二次频率调节的改进方法，在变流器间注入小的交流电流，消除频率偏差的同时避免对功率变流器间功率分配的影响。

由上述控制模式切换相关策略的研究成果可知，模式切换方法大体可分为以下两类：1）根据孤岛-并网逻辑信号切换控制结构，进行定有功-定无功控制结构［19］和定交流电压频率、幅值控制结构［20-21］间的相互切换；2）采用孤岛和并网均能稳定运行的控制结构，孤岛和并网切换过程中仅切换控制目标值，通常可采用下垂控制［22-23］、虚拟同步机控制［24-25］、功率同步控制［26-27］等。其中基于第一类模式切换方法依赖孤岛和并网检测，检测延时通常导致并网冲击，而第二类方法中孤岛和并网工况下采用相同或类似的控制结构，通常由外环直接计算变流器调制信号，暂态过程电流控制能力较弱，容易出现过流导致跳闸。对此本文针对南澳工程中金牛换流站孤岛-并网转换过程提出平滑切换方法，在后续部分分别介绍系统结构、控制器设计、切换方法和所提出控制策略的仿真验证。

1 系统结构

1.1 已有工程中的模式切换方法

南澳柔直系统为三端并联结构，换流站采用基于半桥的MMC拓扑，三端换流站结构相同。其中金牛站和青奥站连接岛上风电场和交流负荷，塑城站连接岸上交流系统。如图1所示，以金牛站为例，存在孤岛和并网两种运行方式，当断路器K1和K2闭合换流站为并网模式，K1闭合，K2断开则为孤岛模式，由换流站为负荷及风电场提供电源。图中P和Q为换流阀输出有功和无功功率，I交流电流，T1为换流变压器。

图1 南澳柔直系统结构Fig.1 System structure of Nanao VSC-HVDC

变流器控制采用常规电网电压定向的矢量控制，在并网运行时，金牛站通常采用定PQ控制方式，孤岛时采用定VF（交流电压和幅值）模式。离并网模式切换过程依赖断路器K1和K2位置信号，存在延时和合闸角度偏差容易出现电流冲击，导致切换失败。尤其在孤岛向并网模式切换过程，VF模式下由电压和频率给定信号直接计算变流器调制信号，没有直接的电流控制回路，暂态电流抑制能力较差，即使配置同期合闸装置，切换至并网运行时仍然存在较大的失败概率，严重影响系统供电可靠性。

1.2 改进的模式切换方法

针对上述问题，设计一种模式切换的“中间状态”，该状态在孤岛和并网工况下均能长期稳定运行，各状态转换关系如图2所示，图中VF控制和P Q控制为常规变流器控制策略。在离并网切换过程中，先切换至中间状态，待断路器位置信号明确后，再平滑切换为常规的孤岛或并网控制模式。其方案主要优势是离并网切换过程不依赖断路器位置信号，以及切换后进入稳态，仍然保持南澳工程原有控制策略，提高切换成功率的同时不影响原有工程的动态和稳态性能。中间状态在并网和孤岛模式下均能稳定运行，以此解决常规P Q和VF控制模式切换过程中，由于网侧断路器位置判断延时导致的系统振荡和不稳定问题。

图2 控制模式状态转换Fig.2 State transition of controlmode

原控制模式切换为图2中“孤岛”与“并网”两种状态的直接切换，切换前后涉及变流器控制结构的改变，即变流器控制的P Q控制结构和VF控制结构的直接切换，并且VF和P Q的切换时刻需要与交流断路器（图1中K2）分、合闸位置时刻同步。而实际工程中机械断路器位置检测通常存在较大的滤波和延时，导致控制结构切换和断路器分、合闸时刻存在偏差，容易导致模式切换过程出现换流阀与交流电网不同步、冲击电流过大等现象。而本文所提出的增加“中间状态”在孤岛和联网模式下均能稳定运行，在该状态下完成换流阀交流断路器的分、合闸操作时，不需要与变流器控制结构转换同步，待断路器位置检测稳定后，再进行变流器控制结构的下一步状态转换，实现控制结构的切换与交流断路器位置判断的解耦。

“中间状态”的控制策略基于下垂控制设计，保持系统在孤岛和并网工况下均能稳定运行，并利用极点配置方法对电流内环附加阻尼控制环节，改善系统动态性能，变流器“中间状态”控制结构如图3所示。

图3 中间状态下变流器控制结构Fig.3 Controlstructure in transient state for converter

图3中包括有功控制回路和无功控制回路，其中有功外环为：频率给定值fref和频率反馈值ffbk经PI1调节器得到有功电流给定值Idref。无功外环为：交流电压幅值给定Eref和反馈值Efbk经调节器PI2得到无功电流给定值Iqref。电流内环为下垂控制结构，其中Idref和有功电流反馈Idfbk的误差经低通滤波后作为下垂控制的输入，经下垂控制系数Kf后得到交流电压矢量角速度的调节量Δω，与其稳态值ω0叠加后得到变流器输出电压角频率ω。经积分环节得到变流器交流电压矢量相位θ。有功控制回路的下垂特性与传统发电机的外特性相似，通过调节输出交流电压频率调整输出有功功率。低通滤波环节抑制高频电流同时使电流控制回路带宽设置在合理范围内。无功电流给定值Iqref和反馈值Iqfbk的误差同样经下垂控制器Kv得到交流电压幅值调节量ΔE，与其稳态值E0叠加。图中虚框分别为dq轴虚拟阻抗环节，由dq轴电流反馈值分别经高通滤波和虚拟阻抗Kid和Kiq后加入d q稳态调制信号，用于加快暂态振荡电流的衰减速度。uvd和uvq为叠加前述各控制分量后最终的d q轴调制信号，uabc为坐标变换后得到的变流器三相调制信号。T1和T2为滤波时间常数。

图3中有功电流和无功电流控制回路为下垂特性，与电力系统中同步发电机有功和无功外特性类似，当交流系统电压频率或幅值偏离给定值时，变流器调节输出的有功功率或无功功率来调节电压频率或幅值，与发电机的有功-频率以及无功-电压下垂特性相同，因此所提出控制结构在孤岛和并网条件下均能稳定运行，本文的有功电流-频率和无功电流-电压幅值的稳态特性如图4所示，图中横坐标为换流阀网侧交流有功电流id和无功电流iq，纵坐标为换流阀交流电压频率f和幅值V，Idnom为期望的换流阀有功电流，Idmax、Idmin和Iqmax、Iqmin分别为换流阀有功和无功电流的上限和下限，fnom为交流电网期望频率，fmax和fmin分别为变流器输出交流电压频率的上限和下限。变流器并网运行时，其稳态运行点由交流系统频率和幅值确定；变流器向无源孤岛供电时，其稳态运行点由孤岛负荷的有功和无功功率确定。变流器并网运行时，暂态过程中需要具有较大的频率调节范围，而在孤岛状态下稳态频率和电压幅值需要在可接受范围内，因此限幅值fmax和fmin用于暂态调节过程中的频率限幅，电压和频率外环均采用PI调节器，通常稳态时交流电压频率和幅值跟踪给定或偏离额定值较小，保持在交流系统可接受范围内。

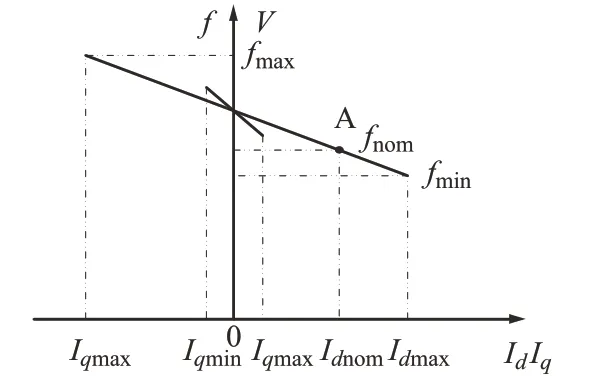
图4 有功电流-频率和无功电流-电压幅值的下垂特性Fig.4 The droop characteristics of Id-f and Iq-V

2 控制结构数学模型

为便于分析系统参数设计和稳定性分析，针对上述控制结构建立单端变流器数学模型。基于阀侧电压定向的同步旋转坐标系将三相交流量变换为直流量，所采用dq坐标系如图5所示，图中usd和usq分别为电网电压定向的同步旋转坐标系dq轴分量，uvd、uvq分别为阀侧电压矢量定向的同步旋转坐标系下dq轴分量。两同步旋转坐标系夹角为θ。

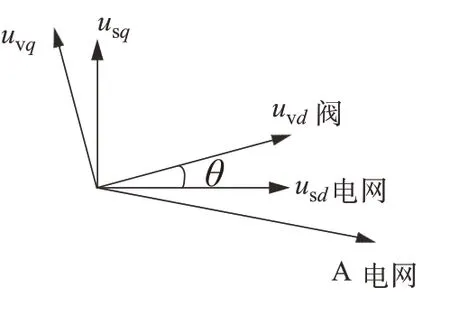
图5 网侧电压和阀侧电压同步旋转坐标系Fig.5 Synchronous rotating coordinate for grid-side and valveside voltage

由图1主回路结构和正方向定义，得到变流器主回路数学模型如式（1）所示：

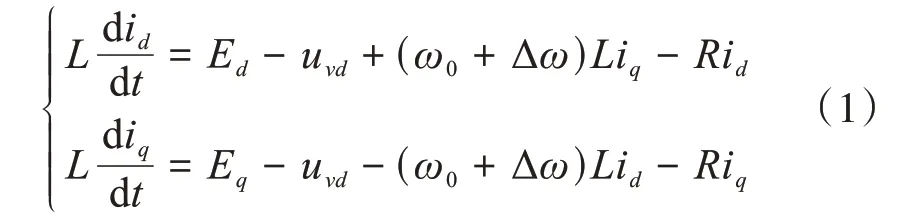
式中Ed和E q分别为电网电压矢量在变流器交流电压矢量定向的同步旋转坐标系上d q轴分量，由图5两坐标系关系可得：

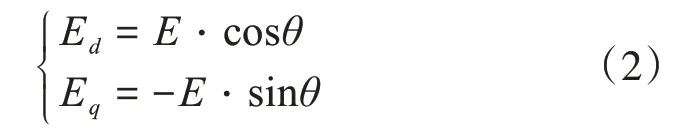
式中E为电网电压矢量幅值。由图3控制结构中ω和θ的关系可得：

由图3中dq轴电流的低通滤波和虚拟阻抗环节中包含两组滤波环节，其动态方程如式（4）所示。

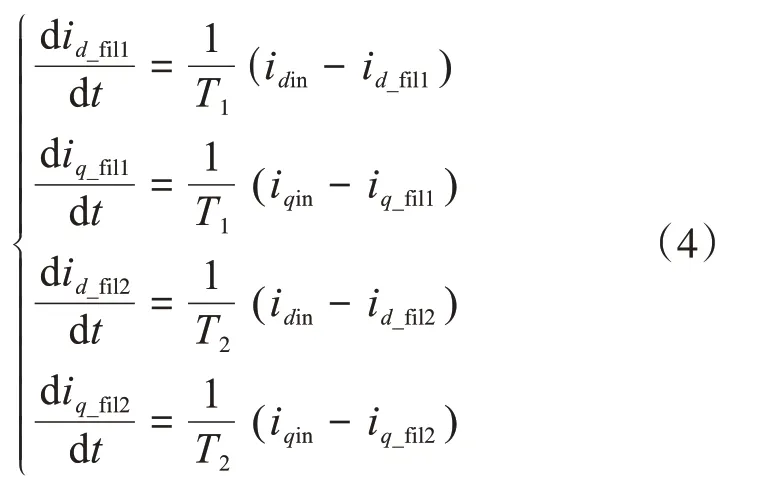
式中：id_fil1和iq_fil1为有功和无功控制回路中低通滤波器输出变量；id_fil2和iq_fil2为dq轴虚拟阻抗控制回路中低通部分滤波器的输出量；idin和iqin为两组滤波器的输入。

由式（1）—（4）可得单端变流器数学模型，为便于分析将式（1）—（4）线性化，并写成如式（5）的形式，为简化忽略式中等效电阻R。

式中：A和B为系数矩阵；x状态变量矩阵；u为输入矩阵。

根据图3所示控制结构，设计控制器状态反馈矩阵K的数值，使得闭环系统特征值在期望的位置上。由图3可知状态反馈矩阵如式（6）所示。

考虑dq虚拟阻抗对称设置，K id=K iq，为验证本文所加入的虚拟阻抗环节对系统影响，保持K v、K f和电流反馈的低通滤波时间常数T1不变，忽略系统中等效电阻，首先验证所建立数学模型的正确性，在状态方程式（5）基础上加入d轴电流给定值I dref的状态变量和输入，设置状态方程的阶跃响应，与实时仿真结果对比如图6（a）所示，图中Idst为状态方程输出的阶跃响应，Idt为实时仿真模型的响应曲线，二者阶跃响应基本重合，证明所建立状态方程的正确性。

图6 系统阶跃响应和电流下垂控制闭环极点Fig.6 Step response of system and closed-loop pole of current droop control

基于系统状态方程分别画出附加虚拟阻抗环节（图3）和断开该回路的系统闭环特征值，如图6（b）所示，虚拟阻抗回路使系统增加两个靠近虚轴的极点，为主导极点，决定系统的响应速度。

3 孤岛和并网切换逻辑

3.1 孤岛至并网模式切换过程

孤岛向并网切换过程包括5个步骤。依次顺序执行如图7所示。

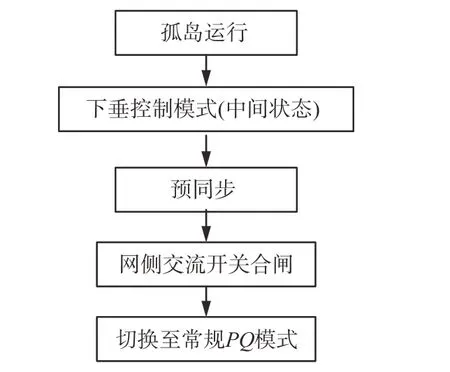
图7 孤岛至并网切换逻辑Fig.7 Switching logic from island to grid

1）孤岛运行，换流阀交流电压相位和幅值均为固定值。即常规的定VF控制。

2）下垂控制模式，在操作员下发并网指令后，变流器按照图2所示状态转换为中间状态，即控制结构切换为图3所示的下垂控制，图中ω0和E0初始值设置为VF控制下输出的角频率和电压幅值，调节量Δω、ΔE和虚拟阻抗环节的输出量均初始化为0，实现VF控制到下垂控制的平滑切换。

3）预同步，调节下垂控制频率给定逐渐偏离额定值，如频率给定值50.5 Hz，使变流器输出电压相位与电网相位偏差缓慢变化。当该相位偏差到达设定范围内时，如±10°，可下发合闸命令

4）切换至常规PQ模式，变流器并网后仍然运行在下垂控制模式，当断路器开关合闸后，确认为并网运行，可切换为常规P Q模式，切换过程相对简单，包括将PQ控制结构中的电流内环调节器给定值初始化为当前下垂控制结构中对应的电流给定值，电流调节器输出值初始化为下垂控制中d q轴当前调制信号值，其他叠加控制量初始化为0，即可实现平滑切换。

在孤岛至并网的控制模式切换过程涉及孤岛模式的VF控制器、中间状态的下垂控制器和并网后P Q控制器，3种状态间控制器切换逻辑如图8所示。

图8 控制器切换逻辑Fig.8 Switching logic of cotroller

图中CMD1和CMD2为模式切换开关，根据控制模式指令选择对应控制器输出，当变流器上位机操作VF-＞中间状态切换时，设置CMD1由1切换为0，CMD2保持为1。当系统交流断路器合闸位置返回后，系统自动设置CMD2由1切换为0，完成孤岛至并网切换过程。

3.2 并网至孤岛切换过程

并网向孤岛切换通常是在交流系统出现故障，由保护装置断开交流网侧开关，对于该种模式转换过程，网侧断路器分合位置的判断延时通常不会造成过大的冲击电流，因此可保持现有模式切换方式不变，在已有的常规P Q控制结构向VF结构切换的基础上，增肌下垂控制结构向常规VF控制结构的平滑转换逻辑即可，如图9所示。

图9 并网至孤岛切换逻辑Fig.9 Switching logic from grid to island

1）初始控制结构，并网向孤岛切换过程可能发生在运行过程的任何时刻，包括变流器运行于常规P Q控制结构或正处于切换的中间状态，即下垂控制结构。因此包含两种初始控制结构。

2）切换为常规VF控制，断路器分闸后，由于原锁相环和系统惯性存在，变流器输出的交流电压频率不会立即大幅度偏离原交流系统额定频率，当检测到交流侧断路器分位时，可通过简单的逻辑切换实现并网至孤岛模式的切换。将常规定PQ控制结构或下垂控制结构在切换时刻的dq轴调制信号直接赋值给VF控制结构，即可实现平滑切换。

并网至孤岛切换过程中网侧交流断路器分、合闸位置信号对切换过程影响较小，可不设置中间状态的过渡过程，模式切换时CMD1=1保持不变，设置CMD2由0切换为1。

如上述稳态VF控制模式或下垂控制结构下，系统仅有VF外环或电流下垂控制环节，与常规的定PQ双闭环控制结构相比，暂态电流控制能力较差，对此可附加文献［28］所提出的峰值电流控制环节，根据本文应用对其简化如图10所示，可改善系统暂态抗扰能力。图中输出峰值电流控制量Dua、Dub、Duc直接与图3的调制信号uabc叠加，所叠加的控制量主要是抑制暂态电流峰值。因此采用比例环节，输出限幅值下限为0，仅当交流电流峰值超过最大运行电流Imax时才参与控制，不影响正常的VF和下垂控制。

图10 暂态峰值电流控制结构Fig.10 Transient peak current controlstructure

4 仿真和分析

基于南澳工程金牛站系统参数在PSCAD下搭建系统仿真模型，其中交流网侧电压110 kV，经110/166 kV变压器与换流阀交流侧连接，直流侧简化为受控电压源，直流电压±160 kV，换流阀为半桥模块化多电平（modular multilevel converter，MMC）拓扑，单桥臂200个模块级联，所采用控制结构如图3所示。本文主要验证在模式切换过程中所设计的“中间状态”在孤岛和并网两种工况下均能稳定运行，解决现有控制模式切换逻辑依赖网侧断路器位置，存在延时的问题，减小切换过程中由于断路器合闸判断延时导致的电流冲击，提高模式切换成功率。由于所提出控制方法主要针对孤岛至并网切换过程，而并网至孤岛切换过程不需要与交流系统同步，切换过程相对简单，仍采用传统模式切换过程，因此不再仿真该过程。仿真初始时变流器交流侧与电网断开，工作于孤岛模式，由直流侧对换流阀供电，变流器运行于前述中间状态，电压幅值和频率给定为额定值，设置t=2 s时加入交流RL负载，t=2.5 s时下发并网命令，并设置输出交流电压频率为50.5 Hz，设置合闸条件为电网电压和变流器输出电压相位差小于3弧度，在大约t=4.38 s时断路器合闸。为验证所提出的控制结构在孤岛和并网工况下均能稳定运行，并网后设置变流器长时间在中间状态下运行。

仿真结果如图11所示，在t=2.5 s前，变流器工作在传统VF控制结下，控制方式t=2.5 s时刻切换，无扰动，在t=2～4 s之间变流器工作在本文所提出下垂控制结构下，始终处于孤岛模式，带电阻和电感（RL）负载运行。图11（a）为11（b）为外环电压幅值、频率调节器的给定和反馈，频率给定值Eref为1.0 p.u.，频率给定值1.01 p.u.（50.5 Hz），频率反馈值ffbk略低于给定，存在稳态误差，偏差在电网可承受范围内，下垂控制结构在孤岛状态下稳定运行。d q轴电流下垂控制的给定和反馈值如图11（c）和图11（d）所示，由于t=2～4 s期间为孤岛运行，系统d q轴电流反馈值由实际负载决定，因此反馈值偏离给定值。在t=4.38 s后，变流器输出电压与电网同步，交流网侧开关合闸，由于有功控制回路中纯积分环节存在，稳态时d轴电流跟踪给定，如图11（d）在t=4～8 s之间波形。而q轴电流始终为有差调节。图10（e）为系统实际输出有功功率和无功功率，孤岛至并网切换过程中功率在额定范围内波动，图11（f）为电流内环虚拟阻抗环节的输出ZK d和ZK q，分别在解锁（t=0.5 s）、突加负载（t=2 s）、并网（t=4.38 s）时输出明显变化，有助于改善系统动态性能，稳态时输出基本为0。由仿真结果可知系统基于下垂控制的有差调节特性，能够在孤岛和并网条件下长期稳定运行，为控制孤岛至并网的平滑切换提供条件。

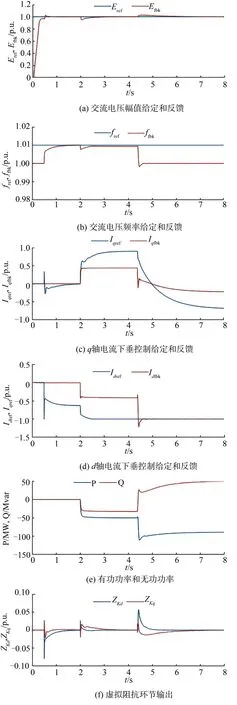
图11 孤岛到并网切换仿真Fig.11 Island to grid switching simulation

为验证所提出控制策略的抗扰性能，变流器在图3所示的下垂控制结构下工作于并网运行模式，在t=6 s后时已进入稳态，设置t=6时发生网侧三相短路故障，持续100 ms后清除，仿真结果如图12所示，图12（a）为网侧三相交流电压Eabc和交流电流Iabc波形，故障期间交流电流主要由峰值电流限制环节抑制故障电流，而电流下垂控制环节主要保证系统稳态运行性能。图12（b）和12（c）为下垂环节电流dq轴给定和反馈信号，与孤岛-并网切换过程类似，稳态时仍然为d轴电流跟踪给定，q轴电流为有差调节，保持系统稳定运行。

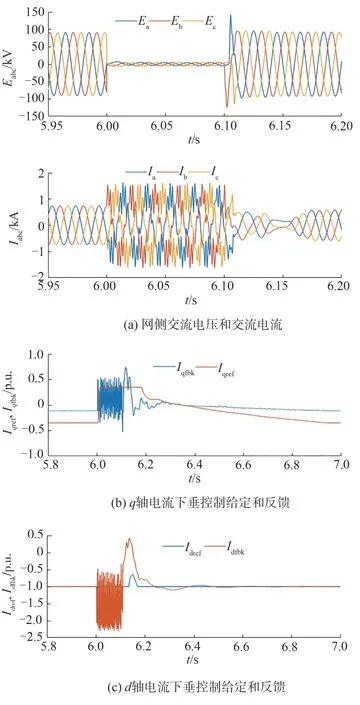
图12 电网三相短路故障仿真Fig.12 Three-phase short-circuit fault simulation of power grid

5 南澳柔直工程验证

南澳三端柔直工程主接线结构如图1所示，其中塑城站连接交流系统，通常工作于定直流电压模式，金牛和青澳站为岛上换流站，交流侧可连接电网或风电场，存在孤岛和并网模式切换，对于岛上两换流站试验方法相同，可根据实际现场情况任选其一。本文选择青澳换流站为试验对象验证所提出模式切换方法。试验步骤如下。

1）设置岸上塑城站与交流电网连接工作于定直流电压控制方式，首先启动，建立系统直流电压。岛上的金牛和青澳换流站初始状态为并网运行方式，运行PQ控制。

2）断开青澳站网侧断路器，青澳站由PQ控制模式切换为VF控制（定交流电压和频率控制方式）。

3）青澳站变流器上位机设置下垂控制使能，青澳站由VF模式切换为“中间状态”的下垂控制方式。

4）合上青澳站交流侧断路器，青澳站控制模式切换为并网运行，控制模式由下垂控制转为P Q控制，完成青澳站孤岛至并网的模式切换。

得到试验结果如图13所示，合闸时交流电流峰值约275 A，切换中的交流电流冲击在保护定值以下，并有一定的余量。与青澳站历史记录的孤岛至并网控制模式切换波形（如图14中2014年录波）比较，图14中切换过程换流阀交流电流峰值约445 A，基于下垂控制的模式切换方法切换过程换流阀交流电流冲击明显小于原控制方法切换电流。试验结果表明本文所提出的下垂控制作为模式切换的中间状态是提高换流阀孤岛至并网控制模式切换成功率的有效手段之一。

图13 改进后青澳站孤岛至并网切换试验波形Fig.13 Test waveforms for switching from island to grid connection at Qing Ao station after improvement

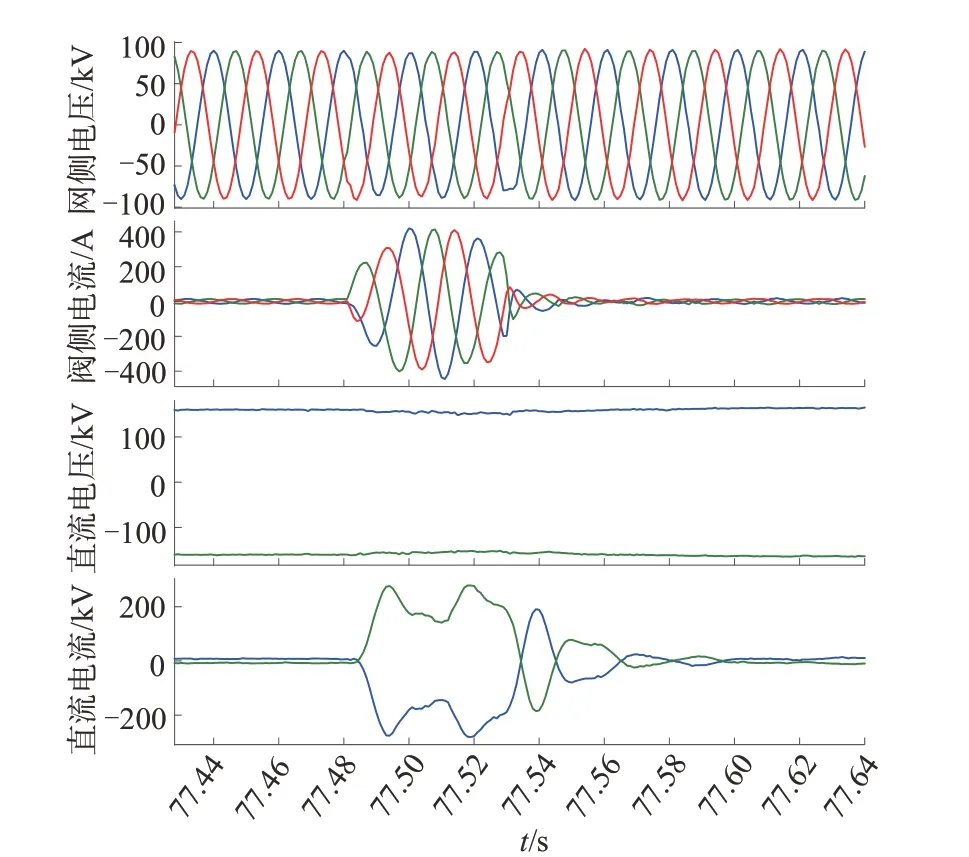
图14 原控制策略下孤岛至并网的控制模式试验波形Fig.14 Test waveform from islanding to grid-connected under the originalcontrolstrategy

6 结语

南澳柔直工程在传统的定P Q控制在并网运行时能够实现较好的动、静态性能，但在模式切换过程中依赖锁相环和网侧交流开关瞬时状态的准确检测，切换过程不可靠，工程运行表明其孤岛至并网运行模式切换过程成功率低的问题较为显著。本文提出切换控制策略中增加模式切换的中间状态，基于下垂控制策略设计电流内环的下垂控制器，并附加虚拟阻抗环节改善系统动态响应速度，所提出控制结构不依赖锁相环与电网同步，在孤岛和并网工况下均能稳定运行，网侧交流开关合闸过程中变流器工作在中间状态，控制器结构不切换，从而解决运行模式切换过程与交流开关位置的耦合。

对于中间状态下所提出的电流下垂控制结构，与同步发电机并网时的同步机制类似，通过调整输出电压相位调节有功功率，控制器外特性也与同步发电机的功率下垂特性相似，因此能够保证孤岛和并网工况下均能稳定运行。该种有差调节特性也能够实现多变流器并联时的功率自动分配。本文所提出的控制方法最终通过青澳站工程验证了其正确性及有效性，减小了切换过程冲击电流，提高了模式切换的成功率，可作为多端系统变流器长期运行的稳态控制策略。