整式概念学习中常见错误例析
⦿湖南省长沙市特殊教育学校 陈赛兰
整式分为单项式与多项式,对单项式与多项式的有关概念,教材中都作了严格的界定.但由于学生对概念的内涵理解不透彻、不到位,导致做题时出错;抑或对概念的外延所包含的特殊对象了解不够,认识不足,导致做题时出错.以下笔者结合实例,作一分析!
1 在区分单项式和多项式时出错
单项式与多项式只有一字之差,但意义却完全不同.单项式是数与字母的乘积组成的代数式,它包括三种类型:单独的数字;单独的字母;数与字母的乘积.单独的数字可以看作字母指数为0的单项式,单独的字母可以看作系数是1或-1的单项式.当整式里的单项式不止一个时,这时的整式就称为多项式,多项式实际上是多个单项式的组合体.
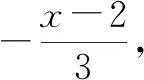
错解:单项式有②⑥;多项式有③⑤.
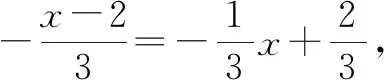
正解:单项式的有①④⑥;多项式的有②③.
例2下列判断错误的是( ).

B.2 020是单项式
C.-a不是单项式

错解:AD.
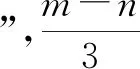
正解:C.
评注:正确理解单项式与多项式的概念是解决问题的前提条件.在区分单项式与多项式时,应着重观察整式中是否含有加号或减号,若含有则是多项式,若没有则是单项式.
2 在确定单项式的系数和次数时出错
在合并同类项时,参与运算的是几个同类项的系数,不变的是字母与字母的指数.而同类项也是单项式,所以确定单项式的系数很重要,它是正确合并同类项的前提.单项式的次数是单项式的一个重要特征,其对于多项式次数的确定至关重要.
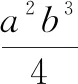
错解:①4;②6.

例4已知(m-3)x3y|m|+1是关于x,y的七次单项式,则m2-2m+2=.
错解:5或17.
剖析:单独的一个数也是单项式,如数0,它的系数是0,次数也是0;15,它的系数是15,次数是0.既然例4中的单项式的次数不是0,那么就必须保证字母的存在.保证字母存在需要满足单项式的系数不能为0,并且所有字母的指数和不为0.根据题意,可得3+|m|+1=7且m-3≠0,解得m=-3.所以m2-2m+2=9+6+2=17.
正解:17.
评注:在确定单项式的系数时,先要把式子写成乘积的形式,然后再找数字因数;在确定单项式的次数时,只关注其中的字母,然后把字母的指数相加即可.
3 在确定多项式的项时出错
多项式的项是指其中的每一个单项式,弄清多项式里的每一项尤为重要.在进行多项式的升降排列时,需要对多项式的某些项重新调整位置,只有理清了每一项,才不会出错;在整式的加减运算中,去括号及合并同类项,都需要变动其中某一项的位置,这也要求学生知道多项式的每一项.
例5多项式2a-3a2b3+4ab2-16的最高次项是,常数项是.
错解:最高次项是5,常数项是16.
剖析:多项式的项是指多项式中的每一个单项式,每个单项式都包括它系数的正负号,所以例5中的多项式的最高次项是-3a2b3,而5是最高次项的次数.常数项是-16,不能丢掉它前面的符号.
正解:最高次项是-3a2b3,常数项是-16.
例6关于多项式-x3y+xy-7,下列说法错误的是( ).
A.是四次三项式 B.最高次项系数是-1
C.不含二次项 D.常数项是-7
错解:AD.
剖析:多项式的项是指多项式中的每一个单项式,每个单项式都包括它系数的正负号.所以例6中的多项式由三项组成,分别是-x3y,+xy,-7.其中-x3y是最高次项,它的系数是-1,次数是4;+xy是二次项,系数是+1,次数是2;-7是常数项.
正解:C.
评注:注意“最高次项”“最高次项的次数”“最高次项的系数”这几个名词的不同,它们主语分别是“项”“次数”“系数”,前面的文字是主语修饰词.虽然研究的是同一项,但所关注的要素不同.
4 在确定多项式的次数时出错
多项式的次数是指在多项式中,比较各单项式项的次数,将次数最高的项的次数作为多项式的次数.多项式的次数是多项式的重要内容,当我们说某个多项式是几次几项式时,首先要确定它的次数;在确定整式方程是几次方程时,实际上也是依据多项式次数的概念进行定义的.
例7若m,n均为自然数,且m 错解:n=4. 剖析:π是圆周率,是一个常数,所以-πn+2也是一个常数.多项式中常数项因为不含字母,所以它的次数为0,从而常数项的次数最低.因为m 正解:n=5. 例8已知关于x,y的多项式x4+(m+2)xny-xy2+3. (1)当m,n为何值时,它是五次四项式? (2)当m,n为何值时,它是四次三项式? 错解:(1)n=4,m为任意实数;(2)m,n均为任意实数. 剖析:(1)多项式x4+(m+2)xny-xy2+3中,第一、二、三、四项的次数分别是4,(n+1),3,0,要使这个多项式的次数为5,则n+1=5,解得n=4.但是第二项的系数是m+2,当它为0时,则不合题意,因此m+2≠0,即m≠-2.(2)要把原来的四项式变为三项式,必须让其中的一项为0,观察多项式可以发现,第一、三、四项都不可能为0,只有第二项有这个条件,因为它的系数是m+2.因此,当m+2=0时,即m=-2,多项式变为三项式,此时n为任意实数. 正解:(1)n=4,m≠-2. (2)m=-2,n为任意实数. 评注:在确定多项式的次数时,只观察含字母的项,在含字母的项中,次数最高的项的次数就是所求多项式的次数.特别注意的是“π”也表示一个数,只不过它是我们将来要学习的无理数.它不是字母. “人非圣贤,孰能无过”!在新知识的学习过程中,由于学生对问题的认识角度及侧重点不同,因此犯一些错误也是正常的.随着错误的纠正,学生对知识的认识会更加深刻,同时,也提高了自身的思辨能力.人生不就是在不断的犯错纠错中成长起来的吗?

