基于蚁群特征选择并行分类集成学习的孪生辐射源个体识别

徐雨芯， 顾楚梅， 曹建军， 许金勇， 魏志虎

(1.南京信息工程大学 计算机与软件学院， 江苏 南京 210044； 2.国防科技大学第六十三研究所， 江苏 南京 210007)

0 引言

随着国际关系的演变和各国军事的发展，各种电台、雷达是战场环境中指挥、控制、通信、情报探测、电子监控等军事活动的基础前端和数据来源，具有举足轻重的地位[1]。掌握军事优势的首要条件是及时获取战场信息，并据此做出正确的战术预测，从而有效打击对方的重要电子装备和载体。从辐射源发射的信号中提取特征信息、识别信号、识别电台是获取战场信息的重要技术手段之一。因此，世界上许多国家都将工作重点放到辐射源个体识别技术的研究上[2]。本文所提出的孪生辐射源指两辐射源个体的工作性能参数、工作环境等条件高度一致甚至基本相同，针对这样的辐射源个体识别定义为孪生辐射源个体识别。

辐射源个体识别也称为特定辐射源识别(SEI)，相关研究主要体现在两个方面：一是从暂态信号(即辐射源非稳定状态下的开机信号)中提取特征，实现辐射源个体识别方法；二是采用基于稳定特征分析的辐射源个体识别方法[3]。暂态信号持续时间较短，在实际环境下截获难度较大，相比之下稳态信号更容易获取，具备更强的操作性，因此基于稳态信号的辐射源信号识别在实际应用中有更强的适用性[3]。

近年来，有不少文献使用基于深度神经网络的端到端的SEI方法，将原始I/Q信号直接输入神经网络，完成端到端的SEI任务。文献[4]将无线电信号识别问题转化为图像识别领域的目标检测问题，提高无线电信号识别的智能化水平和复杂电磁环境下的识别能力；文献[5]提出一种新的基于长短期记忆的递归神经网络，用于射频指纹识别；文献[6]提出一种通信辐射源个体识别的自编码器构造方法，提高了通信辐射源个体识别任务中自编码器的性能；文献[7]提出一种新的基于深度神经网络的射频指纹识别方案，用于硬件特征的自动识别和发射机的分类。这些方法整体性强，但过于依赖神经网络的设计，并且针对不同的原始数据类型都要设计不同的神经网络，可扩展性不强。另外，卷积神经网络更擅长识别二维图像数据，直接处理I/Q数据识别效果会有所降低。

因此，更有效和可靠的方案是将机器学习与信号处理技术相结合，将SEI任务分为两步，一是数据的预处理和特征提取，二是分类器设计和训练。在大多数辐射源信号的研究工作上，通常只使用一个特定分类器进行分类。文献[8]使用支持向量机(SVM)进行分类；文献[9]采用k-近邻判别分类器等。以上方法均对高维特征通过Filter过滤式方法或Wrapper包裹式方法进行降维后[10]，使用单一分类器进行分类。单一分类器难以充分利用特征集合，在低信噪比下准确率不太理想，文献[11]提出一种设计组合分类器的算法，通过改变样本的概率分布，调用子分类器对不同样本分而治之，这种将分类性能彼此互补的子分类器组合或者融合构成新的分类器的思想又称集成学习。集成学习的成功在于保证弱分类器的多样性，弱学习器间的差异性会导致分类的边界不同，将多个弱分类器合并，可以得到更合理的边界，可进一步提高分类性能。

因此，为提高辐射源个体识别的准确率和可靠性，实现孪生辐射源个体识别，本文提出基于蚁群特征选择的并行分类器设计模型。用子分类器输出结果的分布矩阵度量子分类器间的差异性，将不同特征子集输入到并行分类器的子分类器中，使各子分类器分类准确率最高、差异性最大且特征子集规模最小，模型通过蚁群算法进行求解。子分类器权重以其与模型其余子分类器的差异度和可靠度确定，差异度及可靠度越大，当前子分类器所占权重越大。根据不同权重的子分类器预测结果的加权和进行最终决策。实验结果表明，在原始信号、施加10 dB噪声及施加5 dB噪声下，该并行分类器对孪生辐射源个体识别有良好的分类效果。

1 辐射源信号特征提取

由于提升小波包变换具有优良的时频分辨能力和高效的运算效率，因此采用该方法进行特征提取。基于提升小波包变换的特征提取方法分为两类：

1) 最优基小波包分解特征提取方法。在给定训练样本集下，依据某种准则选择最优小波包基，特征提取在最优小波包基分解下进行。如文献[12]提出的距离准则、散度准则，该方法判定准则是依据具体需提取的特征来完成的。因此适用于事先明确特征集(一般与小波包系数直接相关)的情况。

2) 约定小波包分解结构的特征提取方法[13]。依据信号特点约定小波包分解结构进行特征提取，该类方法有利于扩大特征集，为最终选取有效分类的特征提供更多选择。

由于辐射源信号的复杂性，不能事先确定具体特征集，且为获取辐射源信号更多的特征信息，故采用第2种方法进行特征提取。

1.1 提升小波包分解算法

在提升小波包分解系数上定义代价函数En，当分解系数的能量集中在少数几个系数上，多数系数的绝对值很小，则认为对应的基比较好，此时的信息代价函数取值比较小；当分解系数的能量分布比较均匀时，则认为对应的基不好，此时的信息代价函数取值较大。对给定的信息代价函数，如果在所有提升小波包基中，信号在提升小波包基B下分解所得提升小波包系数具有最小的代价函数值，则称小波包基B为信号x(t)相对于代价函数En的最佳提升小波包基。最佳基下的提升小波包分解，提供了一种具有更好能量集中的信号表达。

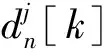
(1)

式中：j=0，1，2， …，CS，CS为分解层数；n=0，1，…，2j-1；L为信号长度。依据信息熵，可以求出具有最小熵的小波包系数，进而求出最佳小波包基。但一般而言求取具有最小熵的小波包系数不易计算，实际应用中通常考虑某个子空间上的小波包分解，即限定分解层数的分解，这种分解可以用一个满二叉树表示，二叉树的所有节点构成了一个基库，根据最小熵准则，从中选取一个满足应用的次优基[14]。

本文采用先序分解后序搜索算法对次优基进行搜索。先序分解后序搜索算法具有与完全分解、自下而上搜索算法相同的时间复杂度，但其分解与搜索同步进行，能及时释放小波包系数所占空间，只记录当前发现较好基对应节点的提升小波包分解系数，空间效率更高。当CS=5时，空间效率提高一倍以上[14]，因此设定CS=5。

1.2 特征提取算法

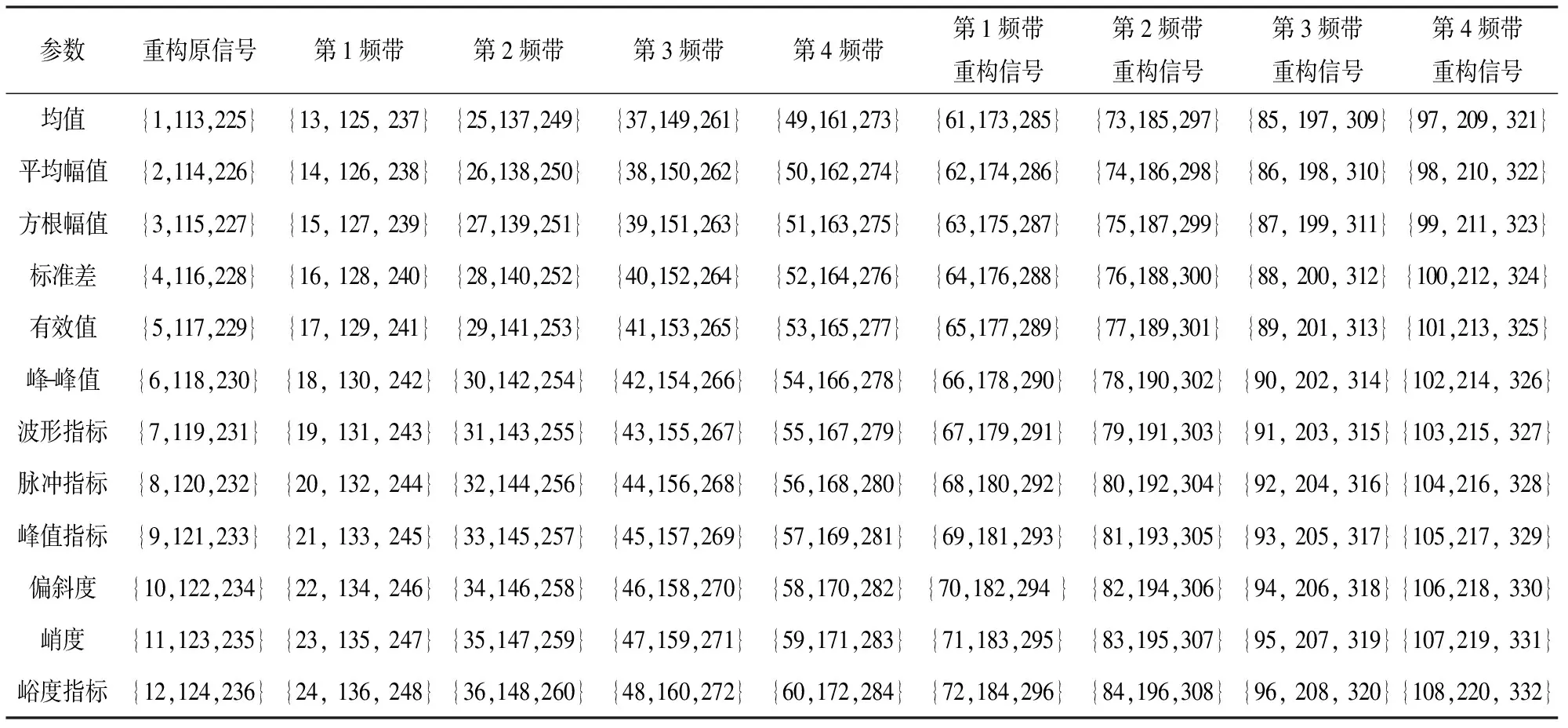
利用提升小波包分解与重构进行特征提取。在不同的提升小波包变换域，对信号的不同成分提取12个统计特征参数[15]，可以得到从不同角度描述信号的特征。统计特征参数分别为均值、平均幅值、方根振幅、标准差、有效值、峰- 峰值、波形指标、脉冲指标、峰值指标、偏斜度、峭度和峪度指标。特征提取算法步骤如下：

1)按先序分解后序搜索算法对数据进行分解，当分解至(4，0)节点时，将此节点系数置零(根据“零”熵最优，此节点不必继续分解)，转到(4，1)节点继续运算，直到完成搜索。在搜索过程中，当需删除(4，0)节点的直系祖先节点的孩子节点时，应首先从最左叶子节点开始对该祖先节点系数进行完全提升小波包重构。

2)将信号进行两层提升小波包分解，利用叶子节点系数，分别提取12个统计特征参数，并提取4个标准化相对能量；

3)分别利用第2层各节点进行单支重构，可以得到相应频带内的时域信号，携带的是相应频带内信号的时域特征，对4个单支重构信号分别提取的12个统计特征参数。

4)利用第2层节点对原信号重构，提取原时域信号的12个统计特征参数。

将原时域信号的12个统计特征参数(1～12)，小波包分解的第2层4个节点系数各12个特征参数(13～60)，4个单支重构信号的各12个统计特征参数(61～108)，及4个标准化相对能量(109～112)，共112个特征参数，依次编号命名。

2 并行分类器模型设计

SVM具有较高的精度和防止过拟合的理论保证，在引入适当的核函数后，可以处理原始特征空间中的线性不可分问题。目前已被应用到很多领域，例如文本分类、模式识别和图像处理等[16]。SVM在解决小样本、非线性和高维模式识别问题中有许多优势[17]，因此本文选用SVM作为子分类器。

对于非线性情况，SVM通过核函数将数据样本从低维空间映射到高维特征空间，使其线性可分，然后在高维特征空间中找到最优分类超平面，使训练样本集中的点尽可能远离最优超平面。常用的核函数有线性核函数、多项式核函数、径向基核函数和Sigmoid核函数等[17]。

2.1 分类器的差异性及其度量

对给定训练样本集，以及功能类型和参数设置相同的二分类器，对于确定的特征子集St(即给定特征向量)，通过特征向量构建新的训练样本并训练分类器，然后用测试样本评估分类器的分类性能，可以将特征子集St映射为一个确定的分类器ΛSt和一个分类器输出分布矩阵P，如(2)式所示：

Λ(St)=(ΛSt,P)

(2)

P=[pii′],i,i′=1,2,…,M

(3)

(4)

输出分布矩阵P中元素pii′为第i类样本被错误分类为第i′类的概率，M=2，nii′表示第i类被错误分为i′类的样本数，Nii′为参加测试的第i类样本数。

分类器ΛSt的相似性可以由结果分布矩阵P的相似程度来度量。对分布矩阵的差异性常见的判别方法有皮尔森相关系数、欧氏距离、曼哈顿距离、切比雪夫距离等。本文采用如下归一化的皮尔森相关系数度量两分类器输出分布矩阵的差异性：

(5)

(6)

(7)

P1=[p1,ii′],P2=[p2,ii′],i∈{1,2,…,M},i′∈{1,2,…,M′}

(8)

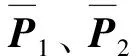
集成学习中的选择性集成思想要求组合分类器中各子分类器有较高的准确率和子分类器之间具有高的差异性，即组合分类器中的各子分类器分类准确率越高，同时它们之间的输出相似性越低，则此组合分类器的分类性能越好。具有此特性的组合分类器，可以确保只有少数子分类器对同一样本同时分类错误。

2.2 基于特征选择的并行分类器设计模型

文献[11]提出一种设计组合分类器的算法，通过对训练样本集进行操作，选择出不同的训练样本子集对分类器进行训练设计分类器，可以得到适应不同样本的分类器，本文利用蚁群算法进行特征选择，从特征选择的角度给出一种新的组合分类器设计算法。基于特征选择的组合分类器设计模型如下：

对含M个(M∈N)分类器的组合分类器，记ρm为第m个分类器的分类准确率，Pj、Pm分别为第j、m个分类器的输出分布矩阵，qm为第m个分类器输入特征子集的基数，采用以下目标函数构造第m个分类器：

maxρm(subsetqm)

(9)

(10)

minqm

(11)

s.t. 1≤qm≤N, subsetqm={t1,t2,…,tqm}

(9)式表明希望所设计的第m个分类器，在当前的特征子集subsetqm下，具有最优的分类准确率；(10)式比较了当前分类器与前m-1个分类器的差异性，选择使得第m个分类器与其他m-1个分类器之间具有最大差异性的特征子集，即互补特征子集，从而最大化分类器的多样性；(11)式表明希望选择基数最小的特征子集，其中N=15。

由于并行分类器由M个子分类器构成，因此需要确定各子分类器所占权重，并对其输出结果进行集成。本文以子分类器的差异度和可靠度确定权重，各子分类器与模型中其余子分类器的差异度和可靠度越大，所占权重越大，根据不同权重的子分类器预测结果的加权和进行最终决策。

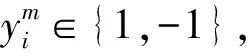
(12)

(13)

(14)

(15)

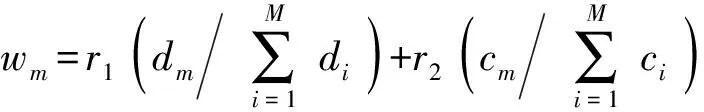
(16)

(17)

(18)

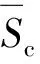
2.3 蚁群算法的设计求解

利用蚁群算法对并行分类器设计模型求解，分析如下：

1)在特征子集基数q确定的情况下，当求解第1个分类器模型时，(10)式并不存在，因此可以直接使用(9)式作为目标函数。当分类器个数大于1时，将(9)式和(10)式加权求和转化为单目标优化函数，如(19)式所示。

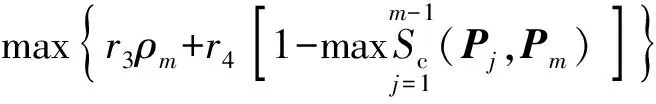
(19)

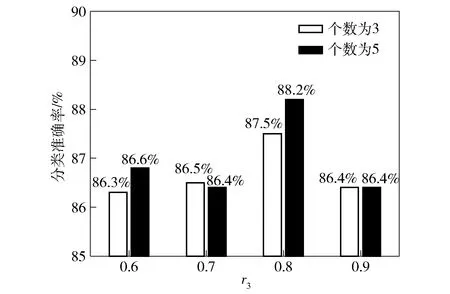
式中：r3与r4是聚合参数，在设计第m个子分类器的过程中，通过聚合参数控制当前子分类器的分类性能与子分类器间多样性之间的平衡。本节通过仿真实验，参数取r3=0.8、r4=0.2时效果较为理想。

2) 对多类分类器而言，特征子集q在5～10之间具有较好的运算效率和分类精度[18-19]，为了不丢失边缘解，将q值的搜索范围限定在1～15之间。

3)算法在当前的特征子集基数条件下迭代完成后，需要为当前分类器选择较好的特征子集。设定转换后的优化目标(19)式的优先级高于(11)式，特征子集基数q不同时，优先选择使得目标(19)式的值较大的特征子集；当两个特征子集的评估值相等时，选择特征基数q较小的特征子集。

根据以上分析，第m个分类器优化设计的具体算法描述如下：

算法1分类器设计算法

输入: 信息素重要程度值α，启发式信息重要程度值β，当前蚂蚁编号ant，每次迭代蚂蚁个数N，蚁群算法当前迭代次数ite，最大迭代次数iter；

输出：特征子集St

1.for 1≤qm≤15 do

2.初始化蚁群算法信息素矩阵、启发式信息；

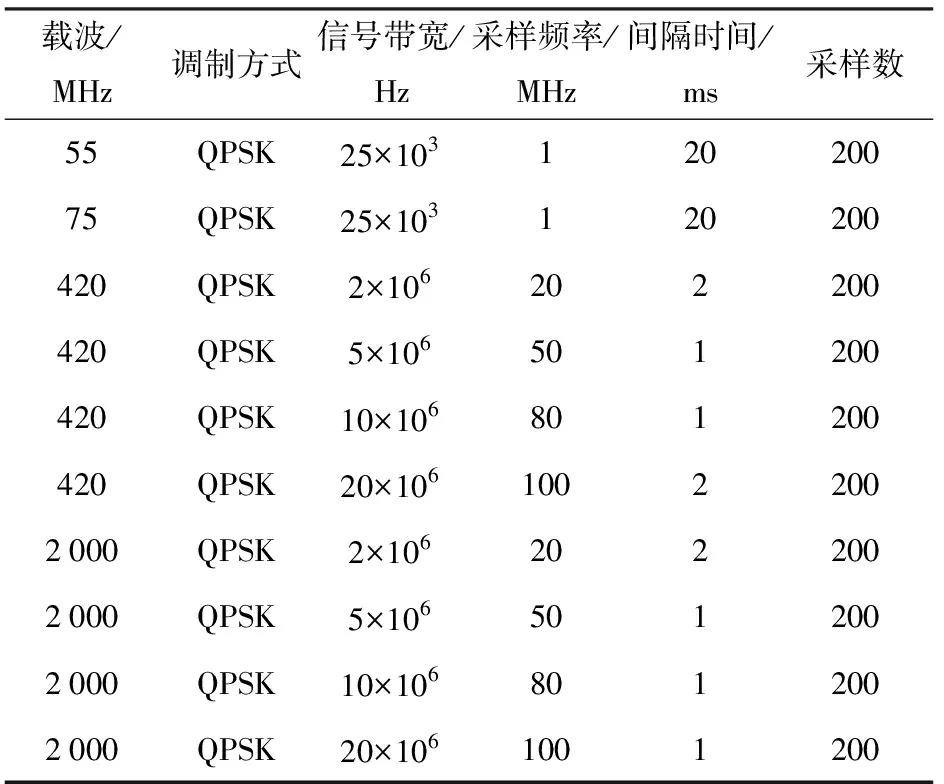
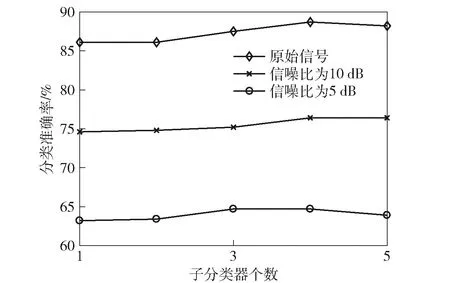
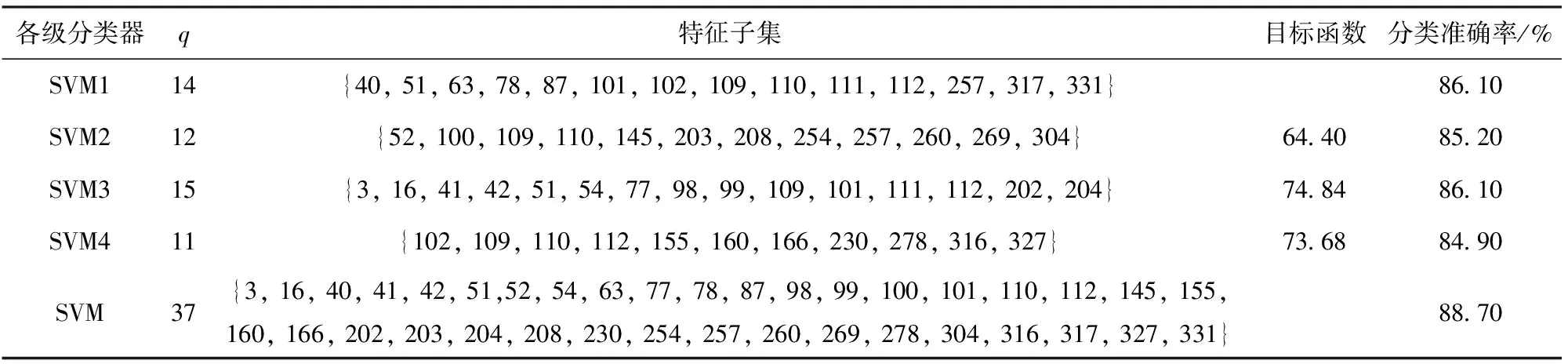
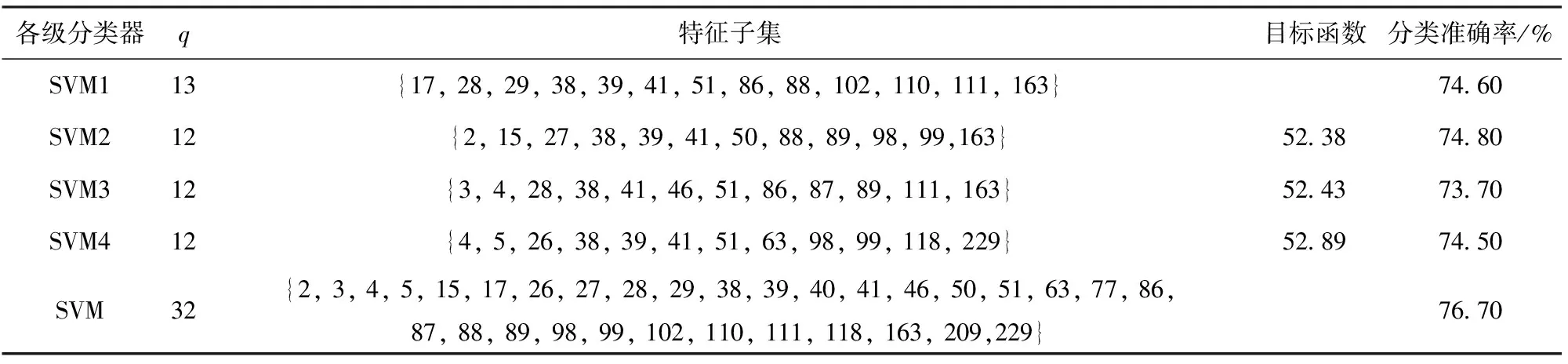
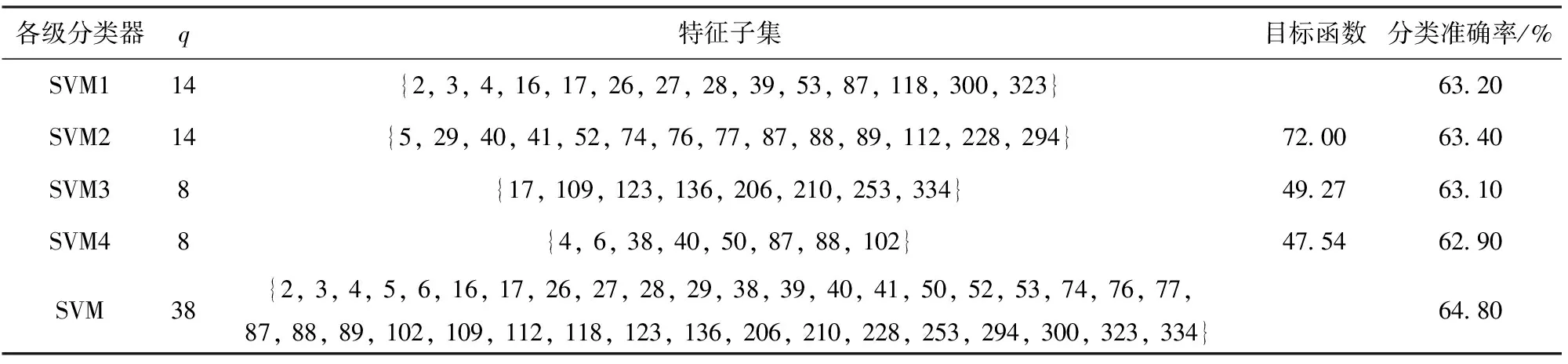
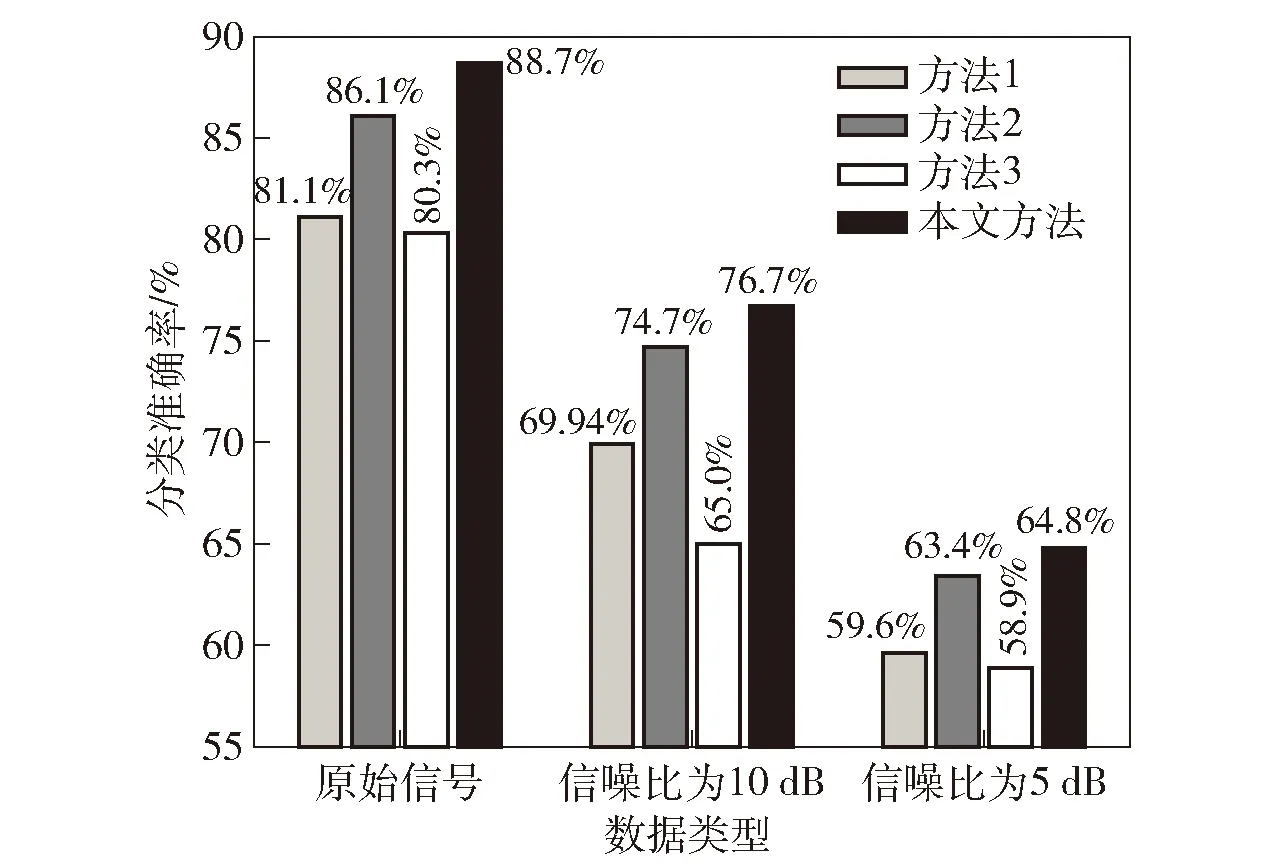
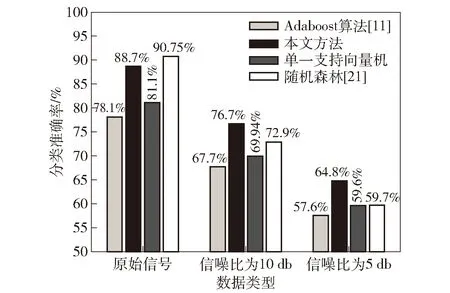
3.whileite

4.for 1≤ant≤Ndo

5.第ant只蚂蚁搜索qm维特征子集；

6.end for

7.按分析1选择特征子集Sqm

并更新信息素矩阵；

8.end while

9.按照分析3 更新当前最优特征子集St；

10.end for

第1行表示当前分类器的特征子集基数；第2～9行是在当前特征子集基数确定的条件下，通过单目标蚁群算法搜索满足优化目标的特征子集；第3～8行是蚁群算法搜索过程；第4～6行是在一次循环中，蚂蚁搜索特征子集的过程；第7行是根据分析1选择较好特征子集并更新信息素矩阵；第9行是根据分析3更新当前分类器的特征子集。

蚁群算法详细设计见文献[20]。

3 实验

3.1 实验数据准备

从电台1、2中采集信号，电台1、2工作性能、采样参数及各参数采样点数均相同，如表1所示。

两电台采集样本数共2×2 000组，每组信号数据分为幅值、I路、Q路3种形式，按1.2节特征提取算法对每种形式下的样本进行特征提取，每组形式提取112个特征，均以12个统计特征参数，4×12个提升小波包二级特征参数，4×12个单分支重建信号特征参数和4个标准化相对能量为序，共提取336个特征。特征编号对应表如表2所示。

表1 电台参数设置Table 1 Setting of station parameters

3.2 实验结果与分析

本文利用分类准确率作为分类结果的评定标准，将不同参数下采集75%的数据作为训练集，剩余25%作为测试集。实验均在PC机上完成，主机配置如下：CPU Intel(R) Core(TM)i7-4770 、3.4 GHz 4核处理器、内存8 GB、操作系统Windows7、编程环境MATLAB R2017a。

记并行分类器子成员为SVM1、SVM2、…、SVMn(n∈N,n>2)，并联构成的组合分类器记为SVM，各SVM子分类器宽度参数g=0.4、惩罚参数C=100。

为确定聚合参数r3、r4取何值时，各不同子分类器个数下的组合分类器能有较好的分类准确率，分 别在原始信号的4组不同聚合参数下进行对比实验，分类结果如图1所示。

表2 特征- 编号对应表Table 2 Features and numbering

图1 不同聚合参数下各组合分类器准确率Fig.1 Accuracy of combined classifiers with different aggregation parameters

由图1可以看出，当r3=0.8、r4=0.2时，子分类器个数分别为3和5的组合分类器分类准确率分别为87.50%和88.20%，均高于r3其余取值下的分类准确率。因此聚合参数取r3=0.8、r4=0.2。

同时，为寻找子分类器个数为何值时，模型分类准确率最高，进行了不同子分类器个数下的对比实验，结果如图2所示。

由图2可知：在电台采集的原始信号下的孪生辐射源个体识别，当子分类器个数为1时，分类准确率为86.10%，即传统单一分类器对原始信号的识别率为86.10%；当子分类器个数为4时，并行分类器的分类准确率为88.70%；当子分类器个数分别为5、6、7时，SVM5、SVM6、SVM7的分类准确率为84.20%、84.40%、84.20%，对应的并行分类器准确率分别为88.20%、88.30%、88.10%。由图2还可以看出，当子分类器个数为4时，分类准确率较单一分类器有一定的提高，表明并行分类器已经具有一定的多样性。当分类器个数再增加时，后续的子分类器未在提高准确率的基础上增加差异性，存在以降低分类准确率而增加差异性的情况，因此子分类器的准确率略微下降，从而导致并行分类器的分类准确率有些波动，又考虑到运行时间，故子分类器个数不再增加。因此在原始信号数据下并行分类器模型的子分类个数设定为4，并联分类器的特征子集为subset37。

对于在原始信号中添加10 dB噪声下的孪生辐射源个体识别，当子分类器个数大于4时，分类准确率未有明显提升，同时考虑到模型运行时间，故模型分类器个数设定为4。此时，分类准确率为76.40%，并联分类器的特征子集q=32。

图2 不同信号下不同子分类器个数的识别效果对比Fig.2 Comparison of the recognition effects of different numbers of subcategories under different signals

类似地，对于在信噪比为5 dB环境下的孪生辐射源个体识别，在子分类器个数为4时，并行分类器的识别准确率更为理想。因此设定此时子分类器个数为4，分类准确率为64.80%，并联分类器的特征子集数q=38。不同信号下的并行分类器模型中各子分类器的特征子集、目标函数等实验结果如表3、表4、表5所示。

表3 并行分类器在原始信号下的分类结果Table 3 Classification results of parallel classifiers using the original signals

表4 并行分类器在加10 dB高斯白噪声后的分类结果Table 4 Classification results of parallel classifiers using signals with 10 dB white Gaussian noise added

为验证最少样本量为何值时，该模型仍有较好的表现，按64%的比例对训练样本量进行递减，分别在数据集大小为3 000、1 920、1 228、786、503、322、206、131、83时，做9组实验，实验结果如图3所示。

由图3可知，该模型在训练集大小为786时，仍有较好的分类效果，此时分类准确率为85.52%，而当训练集小于786时，模型的分类准确率有明显的下降。

表5 并行分类器在加5 dB高斯白噪声后的分类结果Table 5 Classification results of parallel classifiers using signals with 5 dB white Gaussian noise added

图3 不同样本量下的对比结果Fig.3 Comparison results with different sample sizes

同时，为验证提出的模型中创新点的有效性和必要性，进行消融实验。在电台原始采集信号、添加10 dB噪声、添加5 dB噪声3组数据下，分别将本文方法与方法1、方法2、方法3的分类准确率进行对比。实验结果如图4所示。

方法1：未对原始336维特征集合进行特征选择，仅使用单一SVM进行分类。

方法2：使用蚁群算法对特征集合进行选择，但不使用并行分类器，仅用单一SVM进行分类。

方法3：使用文献[21]提出的基于EMD的信号特征提取方法，并使用蚁群算法对特征集合进行选择，在并行分类器下进行分类。

图4 实验结果对比Fig.4 Comparison of experimental results

由图4可知：在3组不同数据下，方法1的分类准确率分别为81.10%、69.94%、59.60%；方法2的分类准确率分别为86.10%、74.70%、63.40%；方法3的分类准确率分别为80.30%、65.00%、58.90%；本文方法的分类准确率分别为88.70%、76.70%、64.80%，均高于其余方法。由此可以看出，本文所提取的特征集合更具完备性，在基于蚁群特征选择的并行分类器集成学习模型中分类效果最好。

最后，由于本文从特征选择和集成学习的角度展开研究，因此将本文提出的模型与文献[11]中提出的Adaboost算法及文献[22]中的随机森林方法进行对比，对比结果如图5所示。

图5 不同方法的分类结果对比Fig.5 Comparison of different classification methods

由图5可知，基于蚁群特征选择的并行分类器的分类准确率明显高于文献[11]和单一分类器，虽在原始信号下准确率略低于随机森林，但在信噪比为10 dB和5 dB的情况下，准确率明显高于文献[21]的方法，抗干扰性更好，更适合实际应用场景。

从上述对比实验可以看出，基于蚁群特征选择的并行分类器模型能充分挖掘特征参数体系的分类能力，在原始信号、添加10 dB噪声、添加5 dB噪声3组不同数据下，均有较好的分类结果。

4 结论

在辐射源信号的二分类识别问题中，常提取到不相关和冗余的高维特征，导致分类器分类性能降低；且当识别的对象为工作性能和工作参数等条件高度一致甚至相似的孪生辐射源时，现有方法分类准确率较低、分类效果较差。本文针对这些问题，提出一种基于蚁群特征选择的并行分类器设计模型，经多组对比实验，该方法切实可行。得出主要结论如下：

1)针对两个工作性能、采样参数等条件均一致的软件无线电电台，首次定义并研究了孪生辐射源个体识别问题，提出了基于蚁群特征选择并行分类集成学习的孪生辐射源个体识别方法。

2)通过最优基提升小波包分解与重构过程，对孪生辐射源按特征参数体系进行特征提取，并利用蚁群算法对高维特征进行特征选择，减少特征冗余和不相关特征，以提高分类准确率。

3)结合集成学习中选择性集成思想，将差异性和子分类器分类准确率作为目标函数，通过蚁群算法对目标函数进行求解，使得并行分类器模型中各子分类器分类准确率最高、差异性最大且特征子集规模最小，并以各子分类器的差异度和可靠度确定权重。子分类器与其余子分类器间的差异度和可靠度越大，所占权重越大，根据不同权重的子分类器预测结果的加权和进行最终决策，提高分类准确率。

目前提出的基于蚁群特征选择的并行分类器设计模型是针对孪生辐射源个体的识别，即二类识别问题，后续研究可以由二分类扩展到多分类，提高模型的适用性。同时，现有的特征集合是按照特征参数体系对辐射源信号在时频域上进行特征提取，下一步可以扩展特征参数体系，以提取更具分类能力的特征，提高分类准确率。最后，可以优化进化算法以提高运算速率等。