利用强化学习开展比例导引律的导航比设计
李庆波, 李芳, 董瑞星, 樊瑞山, 谢文龙
(上海机电工程研究所, 上海 201109)
0 引言
制导规律是指根据导弹和目标的相对运动关系,导引导弹按一定的飞行轨迹对目标实施精确打击拦截。制导规律是导弹精确制导的技术核心,制导规律的研究是精确制导武器研究的关键。
国内外关于末制导规律的研究目前已有大量的理论成果,例如基于最优控制理论的最优制导律[1]、将最优控制理论与微分对策理论相结合的微分对策制导律[2]、基于模糊控制理论的模糊制导律[3]、神经网络末制导律[4]以及被广泛研究的变结构制导规律[5-6]。尽管制导规律的理论成果众多,但受制于工程实现条件,目前在导弹制导中应用最广泛的仍是比例导引末制导律。
由于比例导引规律实现简单、工程易用性强,许多专家学者开展了基于比例导引的进一步研究。李新三等[7]基于模型静态预测规划方法设计了一种协同比例制导律;闫梁等[8]从普适性制导律的角度出发,设计了一种末端碰撞角约束限制的偏置比例制导律;李波等[9]提出一种基于遗传算法的模糊比例导引规律;李辕等[10]设计了针对高速目标拦截特点的三维联合比例制导律;白国玉等[11]提出一种自动选择拦截模式并调整拦截弹速度,兼具顺、逆轨拦截能力的全向真比例制导律;秦潇等[12]考虑用扩张状态观测器对目标的机动形式进行在线估计,设计了一种带有目标机动补偿的反比例制导律;Su等[13]设计了一种考虑零控脱靶以及飞行器间安全距离的偏置比例导引律;王荣刚等[14]提出一种拦截高速运动目标广义相对偏置比例制导律。
关于比例导引规律的扩展研究通常是在传统比例导引的基础上增加修正项,如重力补偿、导弹轴向加速度补偿、目标机动补偿及碰撞角约束等环节。因此无论对于何种比例导引,都无法避开传统比例导引中以视线角速度为输入量的导航比设计过程。文献[15]建议导航比范围为2~6之间,然而这是一个相对宽泛的取值区间,在此范围内的不同取值对导弹制导拦截性能具有显著的影响。
导弹制导拦截的过程实际上是导弹与目标的博弈过程,而导航比的选取问题就是这个博弈过程中制导控制的决策过程。强化学习利用试错法不断与环境交互来改善自己的行为,从而优化自身的应对策略,同时强化学习具有对环境的先验知识要求低的优点,是一种可以应用到实时环境中的学习方式[16-17]。
近些年,强化学习在导弹制导中的应用开始引起学者关注,陈中原等[18]提出基于强化学习的多弹协同攻击智能制导律,用以降低脱靶量和攻击时间误差。梁晨等[19]针对执行机构部分失效条件下导弹对机动目标的拦截问题,提出一种基于深度强化元学习和剩余飞行时间感知逻辑函数的攻击角度约束三维制导律。
本文采用强化学习的方法开展导航比的设计,尝试利用大数据决策替代传统的经验取值设计,解决比例导引规律设计过程中的共性问题,尽可能提升导弹对目标的打击拦截能力。
1 基本设计思路
1.1 比例导引规律

(1)
式中:K为待设计的系数。
导弹和目标的相对运动关系如图1所示。图1中,M表示导弹,T表示目标,v表示导弹速度,vT表示目标速度,η表示导弹速度轴与视线轴的夹角,ηT表示目标速度轴与视线轴的夹角,θ表示导弹速度倾角,q表示弹目视线角,xM为水平方向。
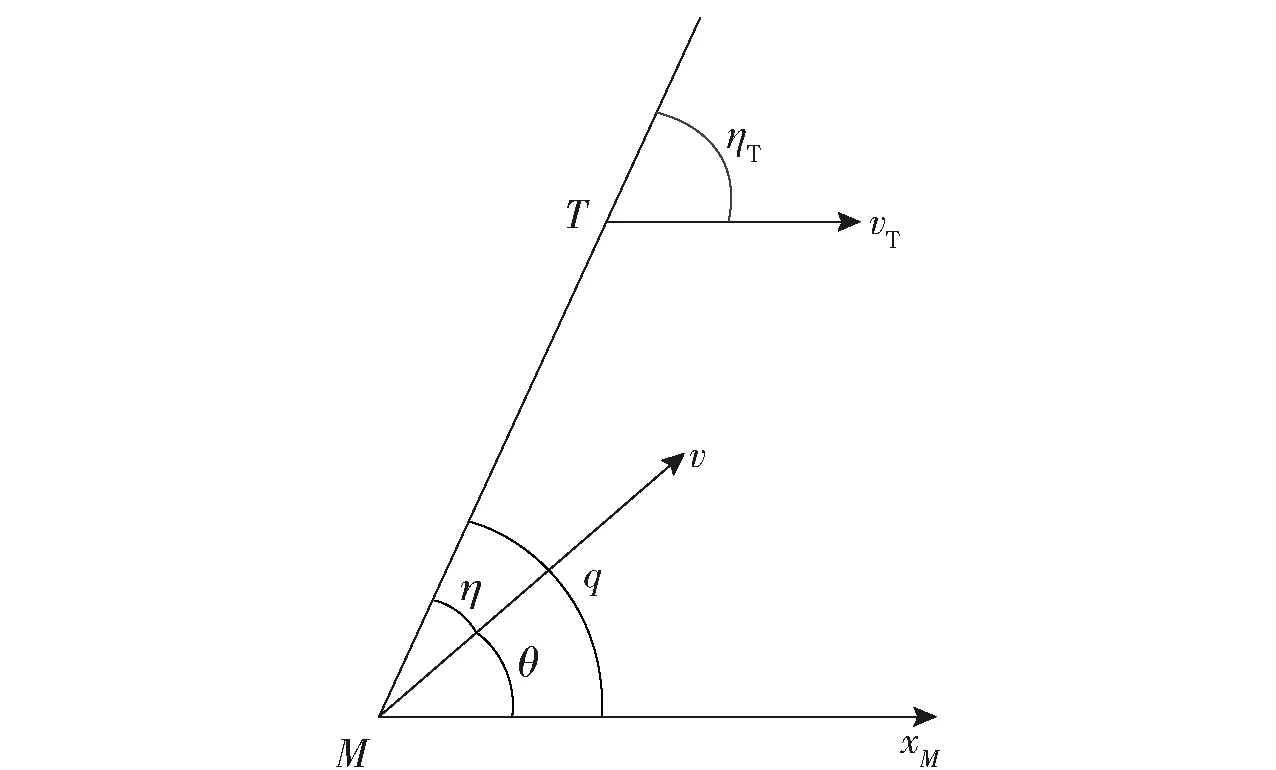
图1 导弹和目标相对运动关系Fig.1 Relative motion diagram of missile and target
(2)
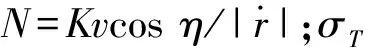
从(2)式可以看出,为保证系统稳定,则要求有效导航比N>2。
在工程应用中,近似认为cosη,可将(1)式改写为
(3)
式中:nc为导弹的过载指令;g为重力加速度。
从(3)式可知,比例导引规律算法简单,且仅需要外部提供弹目相对速度及视线角速度信息,这是比例导引规律能够在工程中获得广泛应用的根本原因。为保证本文的算法具备工程易用性,本文将在比例导引规律的基础上开展设计。
1.2 强化学习基本理论
强化学习任务通常使用马尔可夫决策过程来描述[20]:机器处于环境E中,状态空间为S,其中每个状态为机器感知到的环境的描述,机器能采取的动作构成了动作空间A,若某个动作a∈A作用在当前状态s上,则潜在的转移函数P将使得环境从当前状态按照某种概率转移到另一个状态,在转移到另一个状态的同时,环境会根据潜在的“奖赏”函数R反馈给机器一个奖赏。综合起来,强化学习任务对应了四元组E=〈S,A,P,R〉。图2所示为强化学习原理示意图。
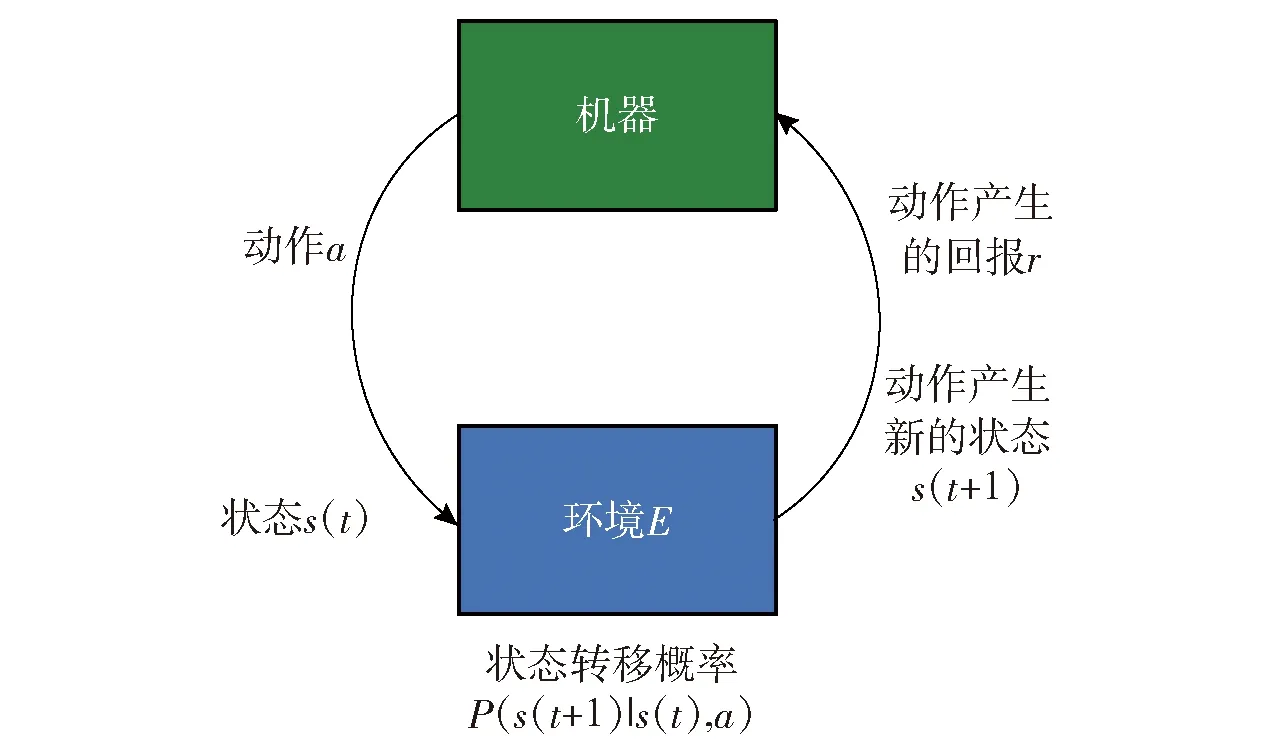
图2 强化学习原理示意图Fig.2 Schematic diagram of reinforcement learning
强化学习的目标是给定一个马尔可夫决策过程,寻找最优策略。所谓策略是指状态到动作的映射,策略常用符号π表示,它是指给定状态s时,动作集上的一个分布,即
π(a|s)=P[At=a|St=s]
(4)
式中:St表示在t时刻或阶段所处的状态;At表示在t时刻或阶段所执行的动作。
策略的定义是通过条件概率给出的,即在状态为s的条件下执行动作a的概率。策略的优劣取决于长期执行这一策略后得到的累积奖励,累积奖励越高,说明策略越好。在强化学习任务中,学习的目的就是找到能使长期积累奖励最大化的策略。
1.3 利用强化学习开展导航比设计的基本思路
为利用强化学习解决导弹制导规律设计问题,首先需将制导规律设计过程转化为典型的马尔可夫决策过程。为不增加工程实现的复杂度,本文在比例导引的基础上,利用强化学习对导航比进行设计。对照马尔可夫决策过程的四元组,建立导航比取值决策过程模型如图3所示。
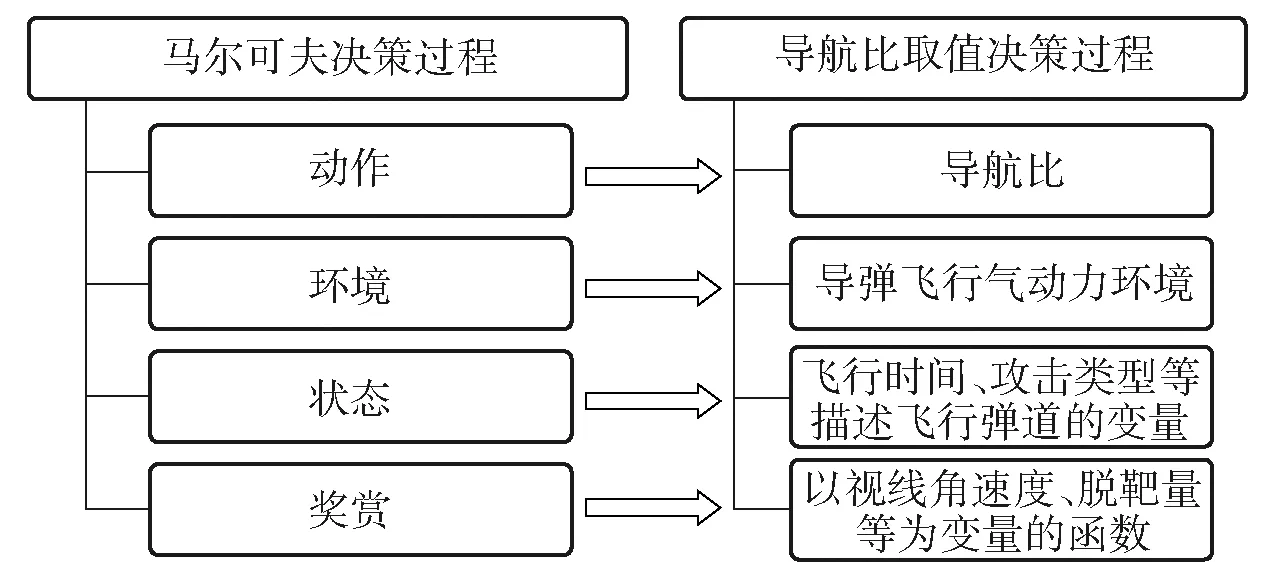
图3 导航比取值决策问题模型关系示意图Fig.3 Schematic diagram of navigation ratio decision model
利用强化学习开展导航比的设计过程可概述为:通过全空域大量典型弹道的仿真计算,评估导弹在不同飞行状态下执行不同导航比策略后的制导效果,按照一定的方法寻求能够获得最佳制导效果的导航比策略。
强化学习多采用ε-贪心或Softmax策略,其目的是在多次采样过程中,既能获得最优的策略,同时也能在采样过程中尽可能获得较大的奖赏。但在进行导航比设计过程中,只关心最终获得最优的导航比策略,希望在采样过程中尽可能获得丰富的样本,而不关心在采样过程中获得的实际奖赏。因此本文中的两种方法均采用“仅探索”的策略开展导航比设计。
2 蒙特卡洛强化学习导引律设计
对标工程实际中广泛应用的比例导引规律,力求设计一种工程应用简单,制导精度更高的导引规律。为尽可能简化算法设计,采用蒙特卡洛强化学习方法。
蒙特卡洛强化学习的基本思想[20]是:进行大量不同策略或不同条件的试验,通过求取每种策略的平均积累奖励作为期望积累奖励的近似,从而完成对策略优劣的评估和策略的迭代。
2.1 四要素的确定与设计
对照强化学习的要素,具体策略求解模型如下:
1)环境E。整个导弹制导仿真模型。具体包含大气模型、基于气动吹风及飞行试验辨识获得的气动参数、发动机推力参数、质量和重心参数、理论弹道模型、控制系统模型、导引头和控制舱等要素。
2)状态S。本节主要考虑工程实际应用,设计一种模型简单、工程实现性强的导航比算法,为此将整个制导的状态进行简化,仅考虑飞行时间和目标攻击方式两个状态。
目标攻击状态集合为{迎攻,尾追};
飞行时间分段离散化集合为{1,2,3,4},具体分段方式如图4所示。图4中,ts为基于飞行时间的分段序号,Tqk为起控时间,Tmz为装定或计算的预计遭遇时间。
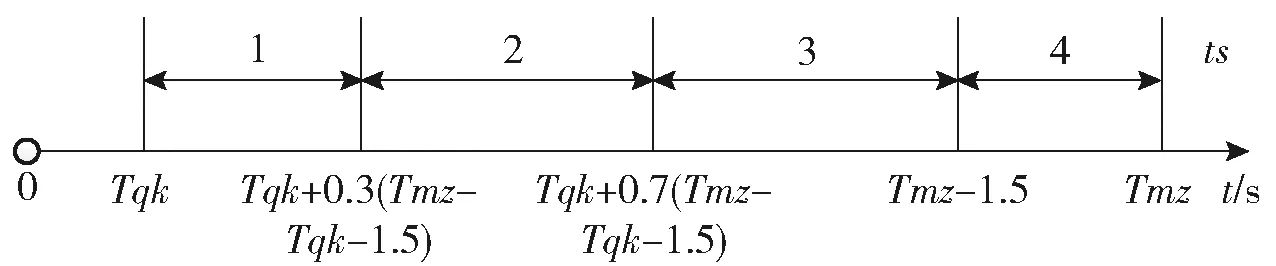
图4 飞行时间分段离散化Fig.4 Flight time piecewise discretization
3)动作A。在不同状态条件下,导航比的取值。将导航比离散化为
N∈[2∶0.2∶6]
(5)
即存在21种导航比的取值。
4)奖赏R。本文的设计是以视线角速度收敛的程度和最终的脱靶量来评估导航比策略的优劣,具体奖赏策略如下:
①视线角速度奖赏策略。将视线角速度进行离散化处理,离散化分段如图5所示。

图5 视线角速度分段离散化Fig.5 LOS rate piecewise discretization
在进行状态切换时,视线角速度由低状态(分段序号较小值)向高状态(分段序号较大值)变化,对上一个状态- 动作对进行惩罚,即给予该状态- 动作对负向奖励;相反,如果视线角速度反向变化,则对上一个状态- 动作对进行奖励,即给予该状态- 动作对正向奖励;如果视线角速度在状态切换过程中仍保持在当前分段,则不进行奖励和惩罚。本文在计算过程中具体采用的关于视线角速度的奖赏算法如图6所示。

图6 视线角速度奖赏策略流程图Fig.6 Flow chart of LOS rate reward strategy
图6中:ss表示执行的弹道序号,共计n条弹道;Dqstate(Sts)表示在Sts状态时,视线角速度分段序号;记录(Tmz-0.3)时刻的视线角速度状态为Dqstate(S5);Rdq(Sts,Nts)表示在Sts状态时,导航比采用Nts所获得的视线角速度奖赏。
②脱靶量奖赏策略。将脱靶量进行离散化并设置对应的奖励如图7所示。
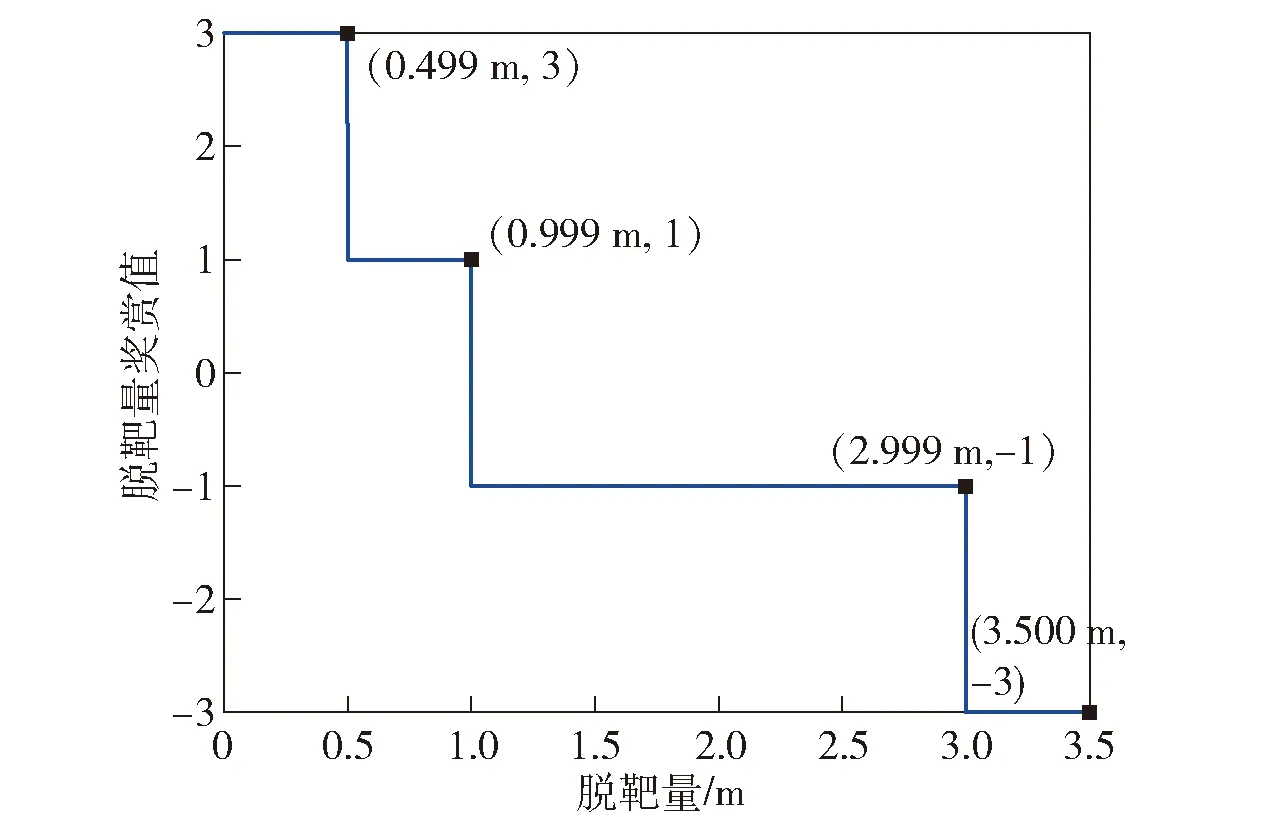
图7 脱靶量奖赏策略示意图Fig.7 Flow chart of miss distance reward strategy
需补充说明地是,为便于描述,本节中的飞行分段、动作集合及视线角速度分段是以某防空导弹为背景的实例化设计,在方法推广过程中需结合应用对象的特性对飞行分段等进行适应性调整,后续章节中的具体分段划分及参数设计也需结合应用对象的特征进行调整。
2.2 策略评估及求解
2.2.1 状态动作值函数计算
强化学习使用状态动作值函数来评估策略的优劣。状态动作值函数用Q(Sts,Nts)表示,表征在状态Sts条件下,导航比采用Nts所取得的平均积累奖励。Q(Sts,Nts)值越大,表明策略越好。
本文利用折扣积累奖赏γ计算不同状态- 动作对的平均积累奖励,以此近似估计状态动作值函数Q(Sts,Nts)。算法实现过程如图8所示。图8中,Rmd(Sts,Nts)表示在Sts状态时,导航比采用Nts所获得的脱靶量奖赏,γ为折扣系数,在本文的实现中,令γ=0.5。

图8 状态动作值函数算法流程图Fig.8 Flow chart of state-action value function algorithm
2.2.2 逐段求解最优导航比
在算法的实际操作中,本文结合导弹制导这一特殊问题,本文设计了一种逐段求取最佳导航比的方法,具体方法如下:
1)将飞行段1、2和3的导航比设定为2~6之间的随机值,通过大量不同弹道,分别计算在飞行段4中不同导航比对应的平均积累奖励R4,其中R4最大时对应的导航比为飞行段4的最佳导航比N4;
2)将飞行段4的导航比设置为最佳导航比,飞行段1和2的导航比设定为2~6之间的随机值,过大量不同弹道,分别计算在飞行段3中不同导航比对应的平均积累奖励R3,其中R3最大时对应的导航比为飞行段3的最佳导航比N3;
3)按照同样的方法获取飞行段2和飞行段1的最佳导航比。具体过程如图9所示。

图9 导航比逐段求解示意图Fig.9 Diagram of navigation ratio piecewise solution
3 基于Q-learning强化学习的多状态自适应导航比设计
第2节中,在进行导航比设计过程中,仅考虑了目标的攻击方式和制导的飞行分段两个方面的状态,在实际制导过程中,涉及的飞行状态远不止以上两方面内容。本节将进一步增加对环境的状态描述,最终目的是设计一种能够根据复杂飞行状态自适应调整的导航比,由于状态变量的增加,导航比设计过程中需要采集更多的样本,进行更大数量级的弹道仿真。为进一步提升学习效率,本节采用Q-learning算法开展导航比的设计。
3.1 四要素的确定与设计
四要素中的环境E和动作A的对应关系与2.1节的设计一致,此处不再赘述:
1)状态S。在本节中,除了对飞行时间进行分段以外,进一步细化了初始装定的目标初始装定速度的大小,将视线角速度状态和遭遇时间也作为对环境的状态描述。首先是对状态进行离散化分段,本文中对各状态的分段方法如图10所示。图10中,ts(Sts)、Dqstate(Sts)、Tmzstate(Sts)、vt0state(Sts)分别表示在状态Sts条件下离散化的飞行时间、视线角速度、预计遭遇时间和目标初始速度的分段值。
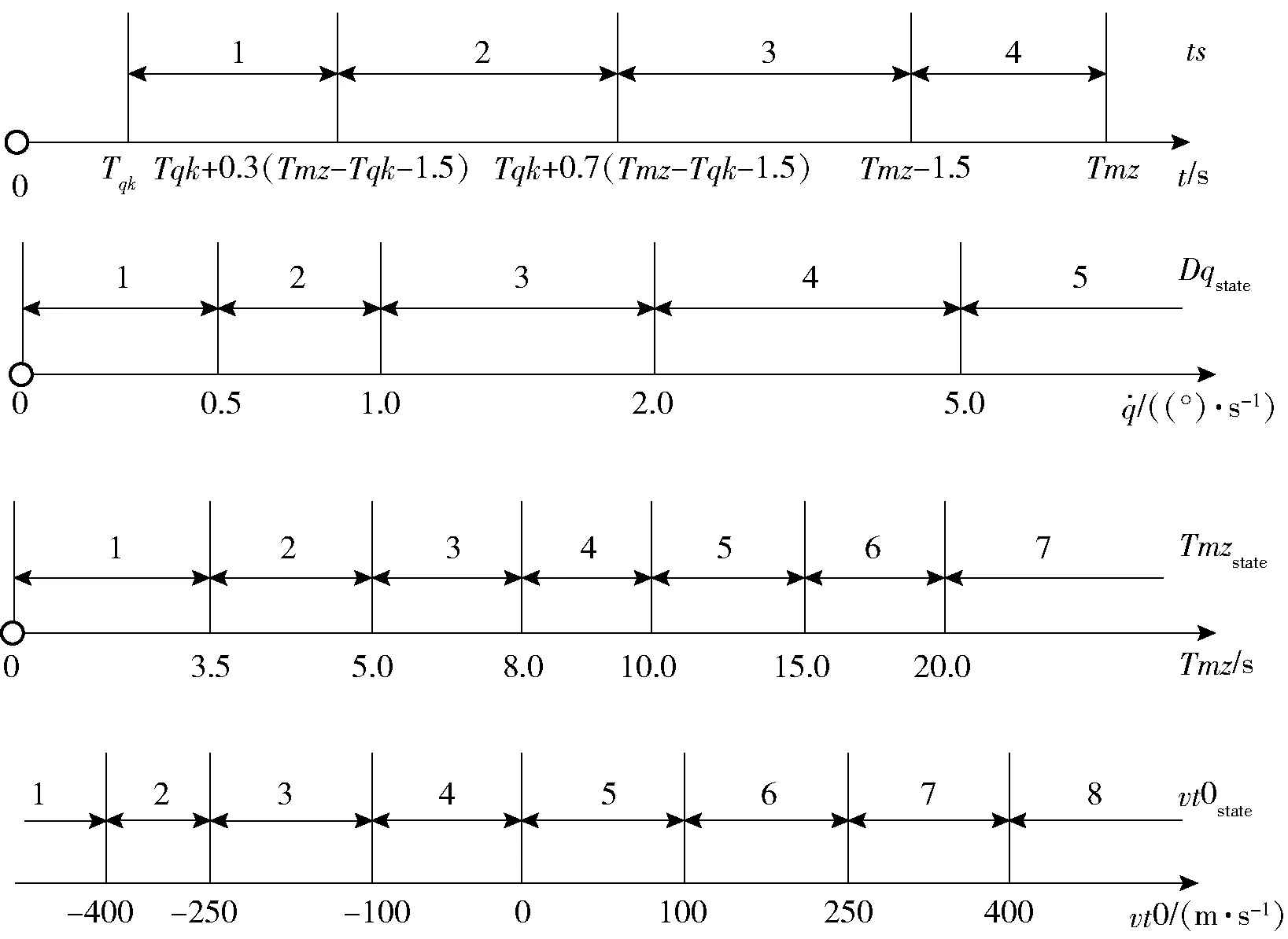
图10 制导状态分段Fig.10 Diagram of guidance state segments
2)奖赏R。由于状态的细分,必须对奖励算法进行相应的细分,否则难以在同一状态下有效区分不同策略的优劣。
视线角速度奖赏策略为
(6)
脱靶量奖赏策略为
Rmd=8e-0.47md-5
(7)
式中:md为最终的脱靶量。
脱靶量奖赏值随脱靶量的大小的变化关系如图11所示。
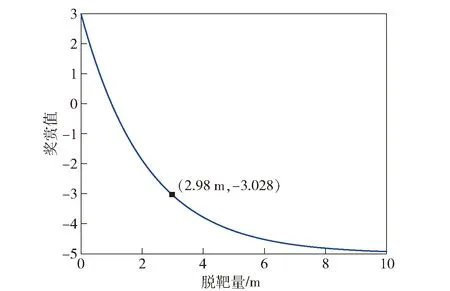
图11 脱靶量奖赏函数曲线Fig.11 Curve of miss distance reward function
3.2 策略评估算法
采用Q-learning强化学习算法进行策略评估,具体算法如图12所示。
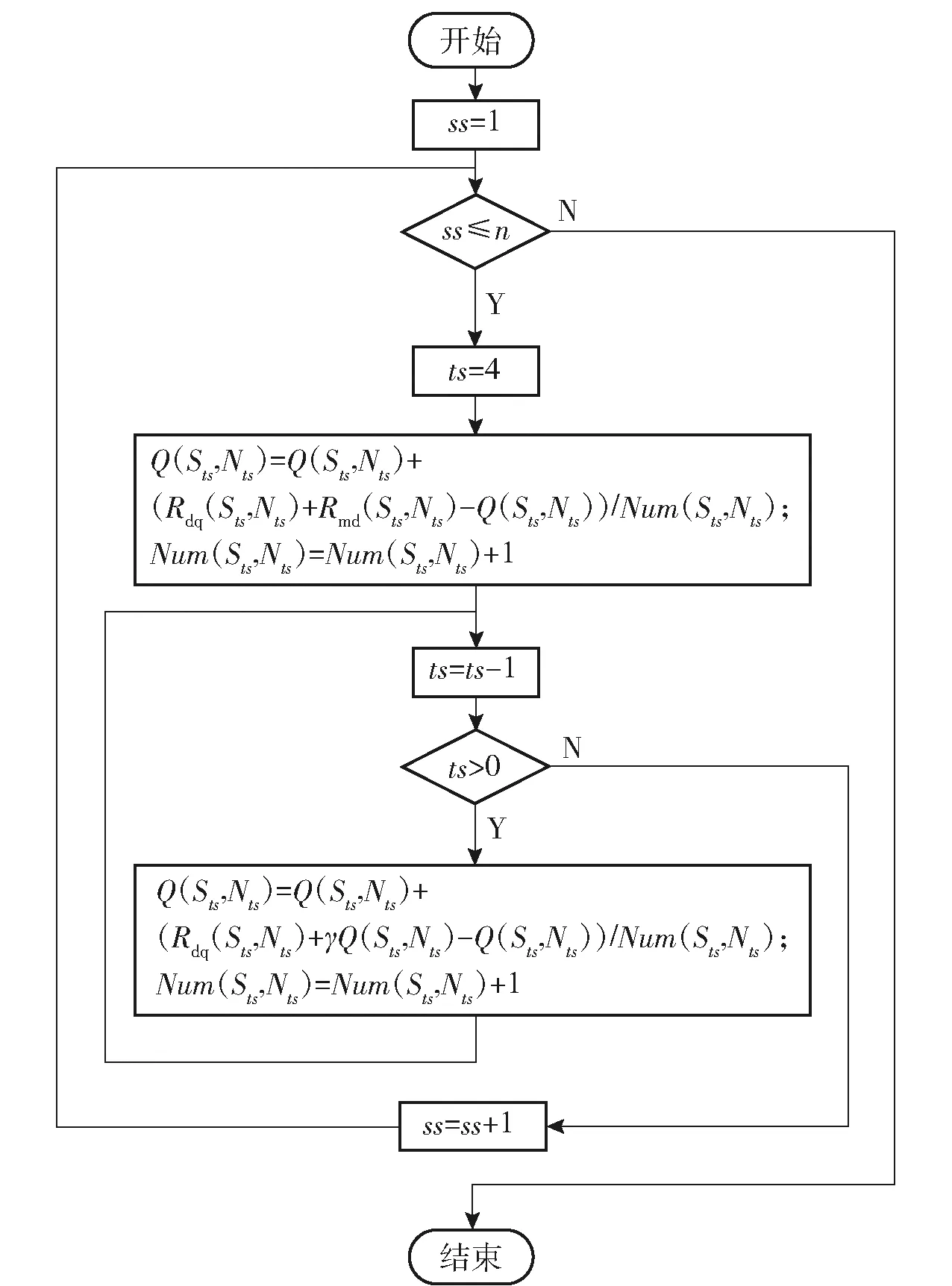
图12 策略评估算法流程图Fig.12 Flow chart of strategy evaluation algorithm
图12中:Q(Sts,Nts)表示在Sts状态时,导航比采用Nts所获得的平均积累奖励;Num(Sts,Nts)表示状态Sts和动作Nts所发生的次数;N′为基于平均概率分布的随机导航比取值,且满足N′∈[2∶0.2∶6]。
4 仿真对比
基于某型防空导弹,分别利用蒙特卡洛和Q-learning强化学习开展导航比设计,蒙特卡洛强化学习设计结果如表1所示。
通过以上设计结果可知,蒙特卡洛强化学习方法设计实现的导航比算法简单,工程易用性强。
根据Q-learning强化学习最终获得的导航比与状态集合一一对应,限于篇幅,本文未列出具体的参数结果。
本文通过从批量弹道中,任意抽取一定数目的弹道,利用3种导航比设计方法开展数字弹道仿真计算,对比不同设计方法下的脱靶量分布情况。
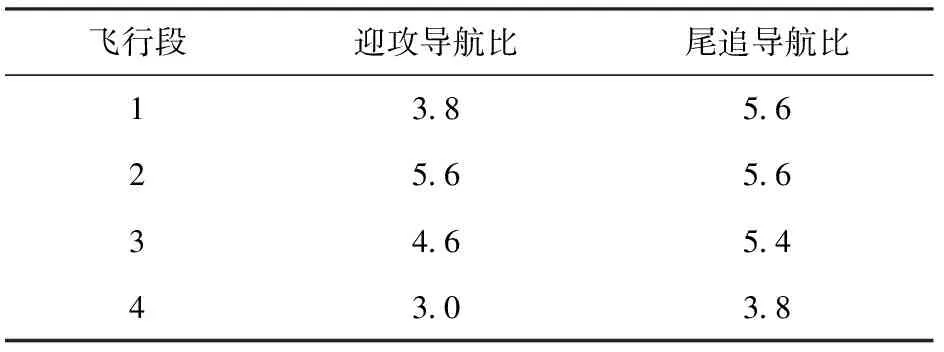
表1 导航比策略表Table 1 Navigation ratio strategies
3种设计方法依次为传统经验设计比例导引规律(APN)、利用蒙特卡洛强化学习设计的比例导引规律(MTPN)和利用Q-learning强化学习设计的比例导引规律(QLPN),其中APN的设计结果涉及到装备技术状态,此处不进行描述。
为避免单次抽取可能存在的偶然性,本文开展了弹道抽样,分别统计每次抽样弹道的脱靶量情况。第1次抽取是从4 789条弹道(受制于篇幅限制,弹道不一一列出)中,每间隔17条弹道抽取一条,共计282条弹道,第2次抽取是从4 789条弹道中,每间隔13条弹道抽取一条,共计369条弹道。选取两个质数(17和13)进行等间隔抽取,可使得两次弹道抽取的重复率较低。
两次基于脱靶量md的弹道计数统计结果分别如表2和表3所示。

表2 第1次不同脱靶量下的弹道计数Table 2 Trajectory number under different miss distances in the first simulation

表3 第2次不同脱靶量下的弹道计数Table 3 Trajectory number under different miss distances in the second simulation
以其中一条弹道为例,对比3种状态下的视线角速度变化曲线如图13所示。
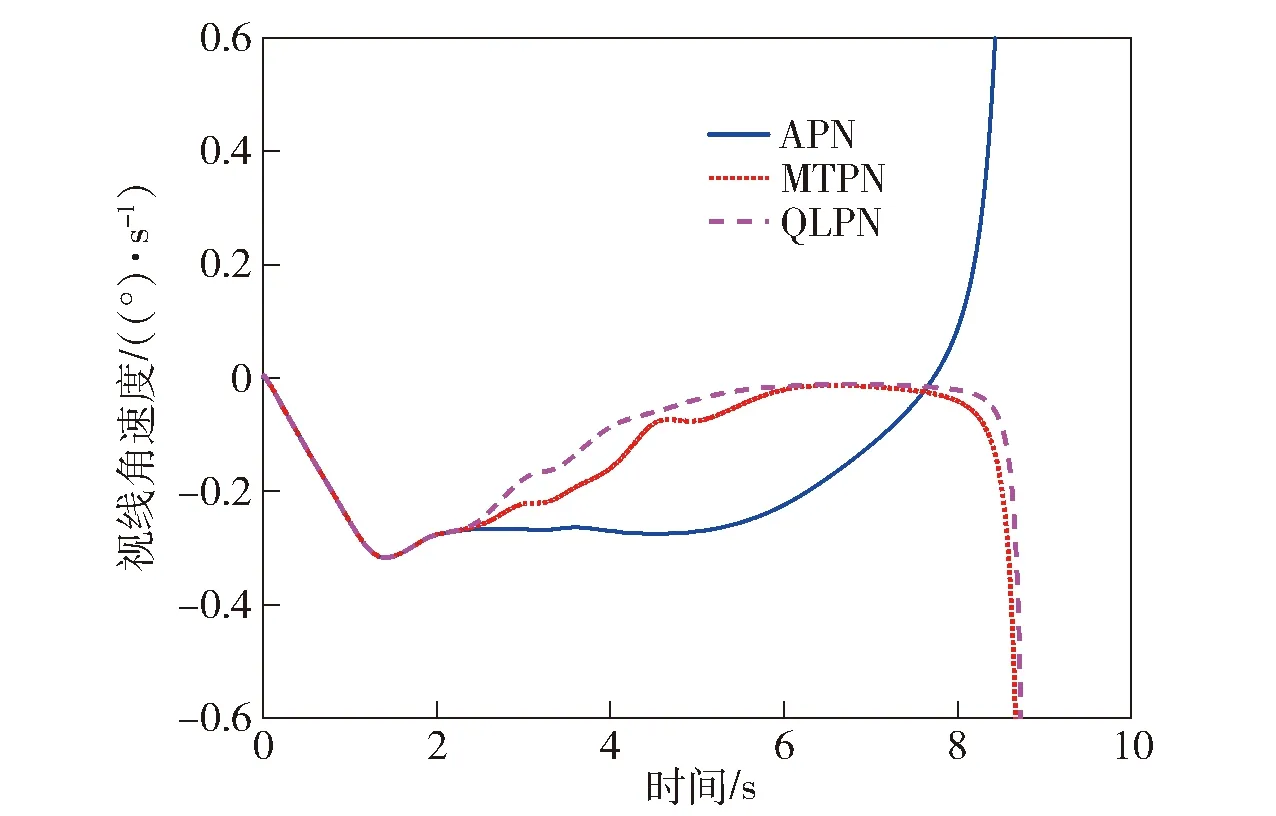
图13 视线角速度对比曲线Fig.13 Line-of-sight rate comparison
从脱靶量的统计结果可知,MTPN比APN在制导过程中具有较为明显的优势,能够有效提升导弹制导精度;而QLPN由于使用了更多的状态对环境进行描述,比MTPN在减小脱靶量方面有进一步提升;从视线角速度曲线对比来看,MTPN和QLPN比APN的视线角速度收敛更快,且在末端发散更晚,同时QLPN略优于MTPN。
5 结论
本文在比例导引的基础上,提出了利用强化学习方法开展导航比设计的思路,通过大数据统计与决策替代传统的经验设计。在此基础上分别采用蒙特卡洛强化学习方法和Q-learning强化学习方法开展了导航比的设计与仿真对比验证。得出以下主要结论:
1)利用蒙特卡洛强化学习的设计方法仅考虑极少的飞行要素,对信息测量的维度和精度要求与工程在用的比例导引规律完全一致,因此具有算法简单,工程应用性强的突出优点,同时在制导精度上相比传统的制导律设计具有显著的提升。
2)利用Q-learning强化学习的设计方法考虑了更多的飞行要素,相比于蒙特卡洛强化学习的方法具有更好的制导性能。但描述环境的状态越多,相应的状态维度就越高,在工程应用中,可根据复杂度的考虑,对描述环境的状态进行删减。
在工程实践中,导引规律的设计还受到一些现实条件的约束,例如雷达导引头视线角速度精度随距离的增加而降低,因此在远距时需限制导航比的取值。本文设计初衷是实现工程化,后续将近一步考虑各种实际约束,实现算法的工程应用与推广。

