基础形式对高填土双孔钢波纹管涵土压力分布规律的影响研究

丁晓旭，牛亚强，张 振，李景茂，陈建军，刘鹏祖，李 凯，祁军良

（1.中铁七局集团 第三工程有限公司，西安 710032；2.兰州交通大学 土木工程学院，兰州 730070）

我国西北地区，黄土丘陵沟壑遍布，当进行筑路工程建设时，高填路基成为主要的通过方式之一.由于高填土工程往往改变了原地表水的排出途径，涵洞成为了路基工程中不可或缺的排水构造物.而在涵洞的服役过程中，一般涵洞在使用3个月至两年即发生不同程度的病害，甚至结构失效破坏，工程界常有“十涵九裂”的说法，土压力是导致涵洞破坏最主要的因素［1-5］，其分布特性成为了涵洞设计必须考虑的关键问题.

1930年，Marston［6］首次在发表的论文中提出了涵顶垂直土压力计算理论，即后来被普遍认可的Marston公式，为后期管涵的设计计算奠定了理论基础；顾安全［7］基于对303座正在运营的管涵调查结果分析及室内试验验证，探讨了各类土压力计算公式存在的问题，并提出了修正计算公式；杨锡武等［8］通过模型试验探讨了不同边界条件的涵洞土压力分布特征，提出受土拱效应影响涵顶土压力小于理论值；李鹏琳［9］通过离心模型试验结合有限元仿真，探讨了不同形式的混凝土刚性基础对涵洞受力变形的影响；郑俊杰等［10］依托工程实例，采用理论分析、数值模拟及现场实测的方法，分析了高填土涵洞土压力分布规律，并对顾安全公式进行了修正.张阳等［11］通过现场测试与数值模拟，研究了双孔管涵的土压力分布与受力特性；杨明辉等［12］依托现场试验，通过理论分析探讨了钢波纹管涵涵顶土压力分布特征及变化规律，指出涵顶平面土压力存在明显的应力集中现象；褚夫蛟等［13］通过数值模拟探讨了大直径管涵的土压力分布规律，认为涵顶土压力较小，而柔性管涵受涵底混凝土基础支撑限制作用导致土压力较大.

分析国内外研究成果，在涵洞土压力分布特性方面的研究日趋成熟，而针对不同基础形式引起的涵洞土压力分布特性的变化规律鲜有报导，更未见双孔钢波纹管涵的土压力分布特性研究成果.基于此，本文旨在探讨高填方工程中双孔钢波纹管涵的土压力分布特性随基础形式不同而呈现的变化规律，依托工程实例通过现场试验结合有限元模拟，综合对比分析，研究基础刚度、圆心角的变化引起的土压力分布特性变化规律.研究成果可为钢波纹管涵在高填土工程中的安全服役设计提供理论依据.

1 现场试验设计

1.1 工程概况

甘肃II-1陇西北部丘陵地区，侵蚀残垣，梁峁沟壑与山川河谷交替分布.某段高填方路基，线路斜跨深切冲沟，堵塞了原地表水宣泄途径，拟埋设双孔钢波纹管涵作为新的排水结构物.现场具体工况信息如表1所列.

表1 基本工况信息表Tab.1 Basic work condition information

1.2 试验测点布置方案

考虑到钢波纹管涵作为一种典型的柔性结构，在填土荷载作用下易发生变形，引起土压力重分布，针对双孔管涵涵顶平面土压力的分布特性，采用如图1所示的测点布置方案.在涵顶平面共布置9个土压力盒，随施工进程以规定频次进行测量.现场管涵布设及土压力盒埋设过程如图2所示.

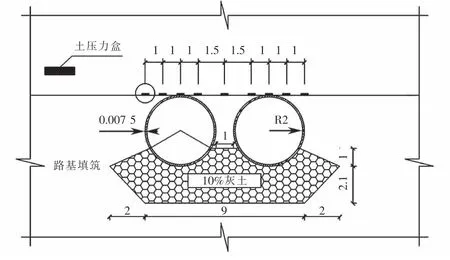
图1 测点布置图（单位：m）Fig.1 Measuring point layout（unit：m）

图2 现场试验Fig.2 Field Test

2 有限元模型

2.1 管涵基础形式选型

不同基础形式引起的管涵土压力分布特性截然不同.依托工程实例，选取不同刚度和圆心角的7种基础形式为研究对象，如图3所示，分析不同基础引起的土压力分布变化规律，具体选型如表2所列，现场采用的基础形式为圆心角120°，10%灰土基础，即基础2.

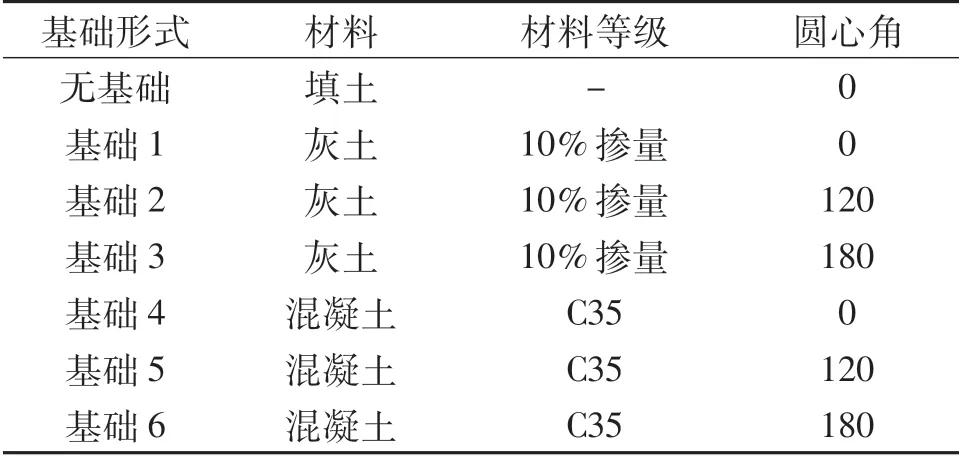
表2 管涵基础形式选型表Tab.2 Pipe culvert basic form selections（°）

图3 管涵基础形式示意图（单位：m）Fig.3 Schematic diagram of the basic form of the pipe culvert（unit：m）

2.2 建立模型

由于波纹管截面形式的特殊性，在模型建立、分析中存在计算困难，文献［14-16］在总结分析国内外钢波纹板截面特性计算理论的基础上，证明了将波纹板的波形简化为正弦函数是切实可行的，并基于刚度等效换算原则，提出了波纹板截面参数换算的一般方法.波形简化如图4所示.

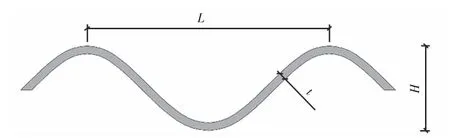
图4 波纹管涵轴向波纹示意图Fig.4 Schematic diagram of axial corrugation of corrugated pipe culvert

采用正弦函数拟合波形如下式所示：

单个正弦波截面积：

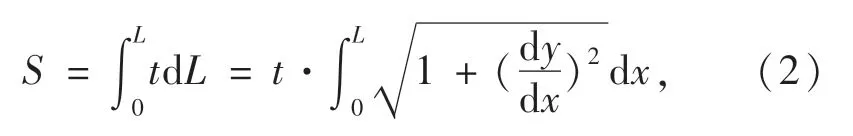
单个正弦波惯性矩：

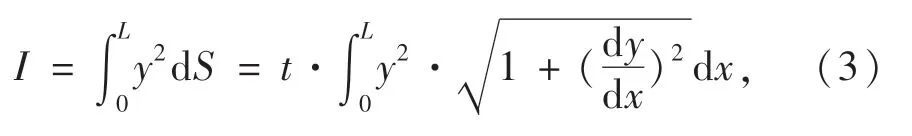
截面等效厚度换算：

波纹管截面参数及计算结果如表3所列：

表3 波纹管截面参数表Tab.3 Corrugated pipe section parameters

采用MIDAS GTS NX有限元软件建立三维模型，模型尺寸X×Y×Z为45 m×20 m×63.8 m，土体和灰土采用摩尔-库伦屈服准则，混凝土和管涵采用弹性准则，模型底面为固定边界，前后及两侧为水平方向固定，垂直方向自由，顶面为自由边界，管涵采用2D板单元模拟，填土分层填筑，层高1 m，涵顶及两侧土体网格加密.模型材料参数如表4所列.

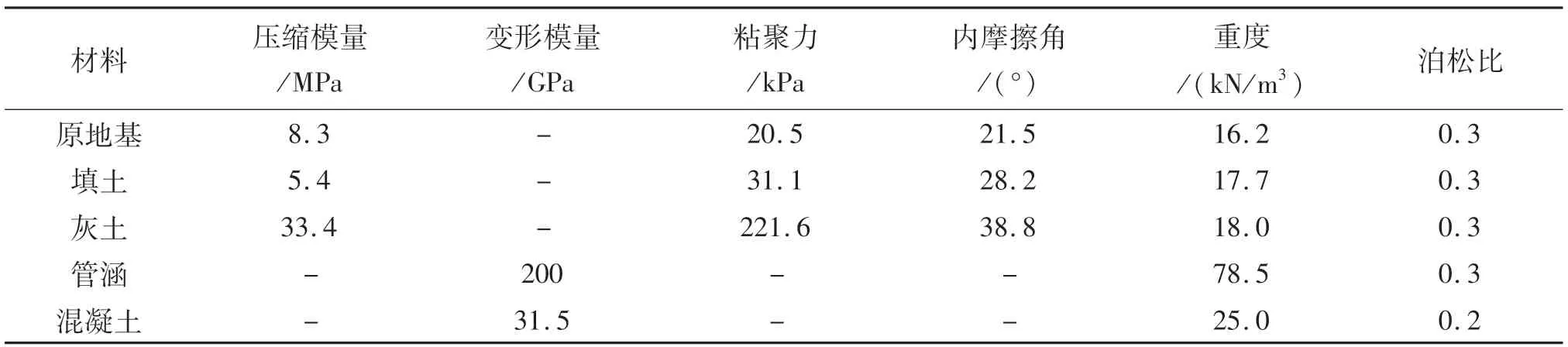
表4 材料参数表Tab.4 Material parameters

有限元模型如图5所示（以基础2模型为例）.

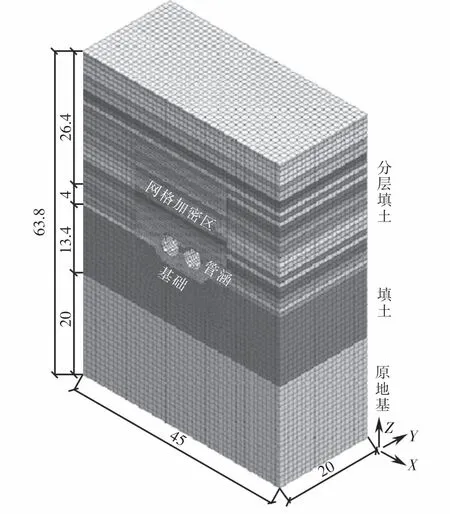
图5 有限元模型（单位：m）Fig.5 Finite element model（unit：m）

3 土压力分布特性分析

3.1 试验与数值模拟结果对比分析

为探讨不同基础形式的双孔管涵的土压力分布特性，建立了不同基础形式的有限元三维实体模型，通过现场试验实测数据与基础2模型计算结果对比分析，验证数值计算的准确性，如图6所示.

由图6可以看到，现场试验测试与数值计算结果对比分析，最大正误差为6.4%，最大负误差为5.3%，测试数据与计算结果虽然存在相对误差，但误差可控，两种方法获得的结果变化趋势一致，证明了有限元模型的正确性.同时可以看出，双孔钢波纹管涵涵顶平面填土土压力分布不均匀，存在多个土压力集中点.

图6 现场试验与数值模拟结果对比分析Fig.6 Comparative analysis of field test and numerical simulation results

3.2 涵顶平面土压力分布特性分析

钢波纹管涵作为一种路基工程中常见的排水构造物，具有良好的变形协调能力，施工过程中随涵顶填土增高，管涵变形逐渐增大，土体提供被动变形抗力，既是荷载同时也是荷载的受体，是一个因果耦合的相互作用过程.双孔钢波纹管涵土压力的分布是在涵侧填土、管涵、涵间土及基础等复杂环境下共同作用的结果.

涵顶平面填土受管-土相互作用影响，因刚度不同而产生差异沉降.双孔钢波纹管涵整体处于对称状态，选取右侧管涵为研究对象，以两涵之间中心点为坐标原点，对比分析不同基础的管涵涵顶平面填土在2.5 m（涵顶）、1.5 m、3.5 m、4.5 m的沉降规律，如图7所示.图7（a）以无基础时涵顶填土沉降为参照，绘制其他基础形式相对于无基础时涵顶填土的相对沉降曲线，图7（b）、（c）、（d）中不同基础形式的管涵分别以自身管涵涵顶填土沉降为参照，分析同一种基础形式在不同位置相对于涵顶填土的沉降.

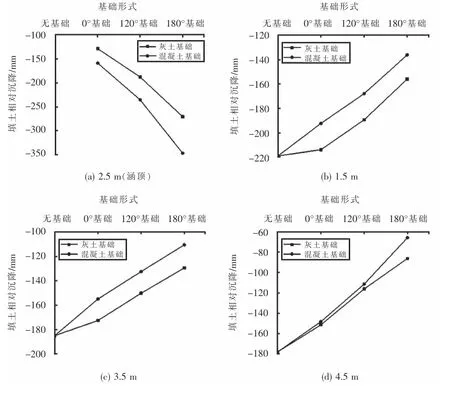
图7 不同基础形式的涵顶平面填土沉降规律Fig.7 Settlement law for culvert top plane filling with different foundation forms

由图7（a）可以看出，无基础时涵顶填土沉降最大，随圆心角增大，填土沉降减小，相同截面形式的基础管涵，基础刚度增大，沉降减小；由图7（b）、（c）、（d）可以看出，涵顶平面填土存在明显的差异沉降，涵顶位置沉降最大，这是由于钢波纹管涵具有良好的变形协调能力，在涵顶填土荷载作用下，发生了收敛变形，导致涵顶沉降增大，在涵顶两侧1 m位置，即1.5 m、3.5 m处，填土沉降相比涵顶较小，在4.5 m位置，即管涵内外土柱的分界点，填土沉降相比涵顶较小，而相比于1.5 m、3.5 m位置较大，这是由于涵侧土体刚度较小，沉降较大，而管涵内土柱受管-土相对刚度的影响，同时管涵自身变形也会引起填土非均匀沉降，导致涵顶平面填土沉降曲线出现了尖点，可以看出，基础圆心角增大，各位置相对于涵顶填土沉降均减小，同时，基础刚度增大也会导致相对沉降减小，说明圆心角及基础刚度增大对于管涵的变形约束作用增强.

填土沉降规律决定了涵顶平面垂直土压力的分布，土体间的相对滑动摩擦作用，使得沉降量大的土体对周边土体产生向下的拖拽作用，传递荷载，分散土压力，同时引起局部土压力集中.不同基础形式的双孔钢波纹管涵涵顶平面填土垂直土压力分布规律如图8所示.

图8 不同基础形式的涵顶平面填土垂直土压力分布Fig.8 Vertical earth pressure distribution of culvert top plane filling with different foundation forms

由图8可以看到，在沉降量最大的涵顶土压力较小，无基础管涵涵顶土压力最小，为451 kPa，受土体沉降摩擦作用，在涵顶两侧1 m附近区域，土压力最大，存在明显的集中现象，随距涵顶距离增大，土体的摩擦拖拽作用减弱，土压力逐渐减小，涵侧土压力逐渐趋于平缓，近似等于土柱压力.随基础圆心角增大，涵顶及涵顶两侧1 m附近区域土压力逐渐增大，基础材料为灰土时，基础1涵顶土压力为488 kPa，基础3为507 kPa，同比增长19 kPa；涵顶两侧最大土压力从534 kPa增大至583 kPa，同比增长49 kPa.基础材料为混凝土时，基础4涵顶土压力为497 kPa，基础6为552 kPa，同比增长55 kPa；涵顶两侧最大土压力从552 kPa增大至624 kPa，同比增长72 kPa.可以看出，基础圆心角增大与管涵的接触面积增大，限制管涵发生过大变形的同时结构整体刚度提高，土体沉降减小，土压力增大.分析填土、灰土、混凝土3种不同刚度的基础，可以看出管涵基础刚度增大，将导致涵顶平面填土在涵顶及涵顶两侧1 m附近土压力集中，不利于管涵承载.

3.3 涵周土压力分布特性分析

管-土作用是一个系统的相互作用体系，管涵受涵顶填土荷载作用下变形挤压周边土体，周边土体提供被动变形抗力，约束变形，在相互耦合作用下涵周土压力趋于均匀分布，合理的涵周土压力能够有效提高管涵承载力［17-18］.

计算结果分析中将管涵等角度划分，提取各测点数据，以涵顶位置为0°起始点，逆时针方向旋转，径向以指向管涵外围为正，如图9所示.

图9 环向测点坐标轴示意图（单位：（°））Fig.9 Schematic diagram of the coordinate axis of the circumferential measuring point（unit：（°））

不同基础形式的双孔钢波纹管涵涵周径向土压力分布如图10所示.

由图10可以看到，7种基础的管涵涵顶径向土压力延管涵两侧逐渐增大，最大位置在30°、330°附近，这与图8涵顶平面填土垂直土压力分布规律一致.无基础、基础1、4涵顶径向土压力分别为471 kPa、507 kPa、514 kPa，基础2、5分别为493 kPa、518 kPa，基础3、6分别为510 kPa、561 kPa，可以看出，同种截面形式的基础随刚度增大涵顶土压力增大；受相邻管涵影响，30°位置各基础形式的管涵土压力相近，差异性不明显，330°位置径向土压力分别为547 kPa、552 kPa、599 kPa、603 kPa、556 kPa、637 kPa、655 kPa，随基础刚度、圆心角增大而明显增大.在0°～180°之间，7种基础最大径向土压力分别为615 kPa、654 kPa、632 kPa、753 kPa、764 kPa，1 554 kPa、1 489 kPa，分别出现在90°、90°、120°、90°、165°、120°、90°位置；在180°～360°之间最大径向土压力位置与0°～180°之间最大径向土压力位置对称，7种基础分别为512 kPa、515 kPa、691 kPa、604 kPa、625 kPa、1 626 kPa、1 457 kPa，可以看出，基础刚度增大直接导致管涵径向土压力集中，集中区域主要在管涵、填土和基础三者的接触点位置，柔性基础包裹管涵区域径向土压力分布较为均匀，有利于保持管涵稳定性，防止发生失稳破坏；涵间土受管涵水平变形挤压，致使靠近相邻管涵一侧最大径向土压力整体大于另一侧，管涵处于非对称受力状态.

图10 不同基础形式的涵周径向土压力分布（单位：kPa）Fig.10 Radial earth pressure distribution around culvert with different foundation forms（unit：kPa）

3.4 双孔管涵与单孔管涵涵周土压力特性分析

由上述分析双孔管涵处于非对称受力状态，选取基础2管涵为分析对象，通过数值模拟计算，对比双孔与单孔管涵涵周土压力分布特性，如图11所示.

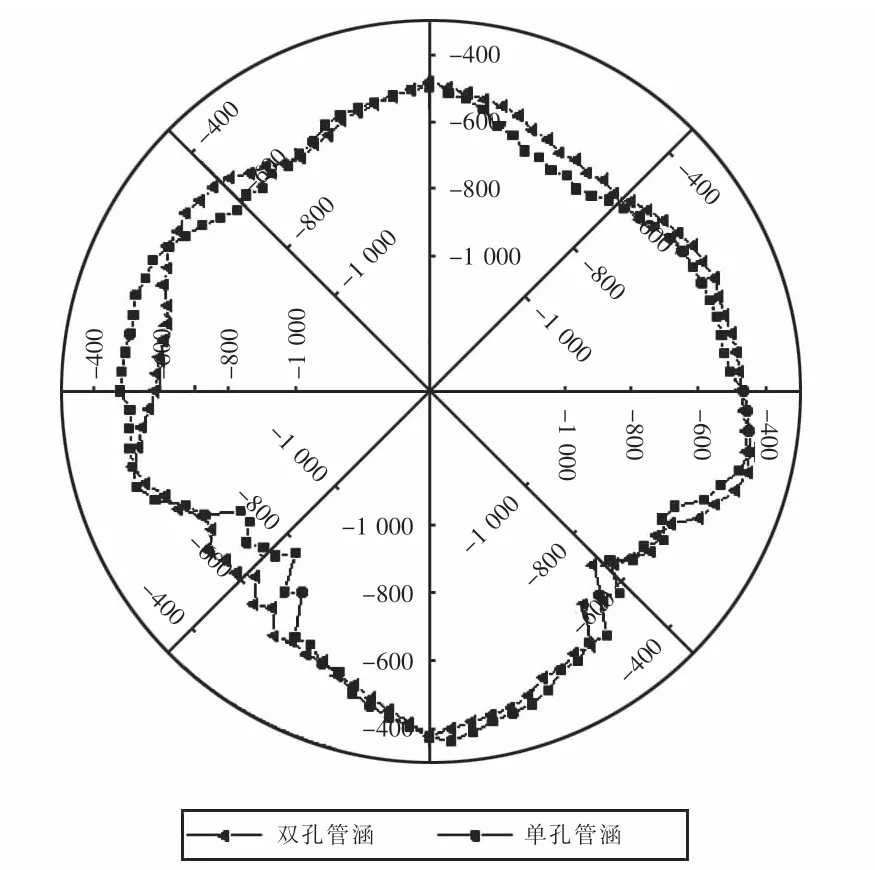
图11 双孔与单孔管涵涵周径向土压力分布（单位：k Pa）Fig.11 Radial earth pressure distribution around doublehole and single-hole pipe culvert（unit：kPa）

由图11可以看到，双孔与单孔管涵涵周土压力分布在180°～360°之间变化趋势一致，数值相近，在0°～180°之间则存在明显的差异点，在45°附近，双孔管涵土压力明显小于单孔管涵，同比相差100 kPa，在75°～90°之间，双孔管涵土压力明显大于单孔管涵，最大差值为106 kPa，针对双孔管涵与单孔管涵涵周土压力在不同区域呈现出的差异性，可以看出双孔管涵处于非对称受力状态，径向土压力在水平轴线附近增大，即土体提供了更大的被动变形抗力，有利于管涵变形控制.

4 结论

1）在填土荷载作用下，管涵竖向收敛变形导致涵顶填土沉降大于涵顶两侧，土体产生相对滑动，通过摩擦拖拽作用传递荷载，各类基础涵顶土压力均小于两侧位置，最大土压力出现在涵顶两侧1 m附近.

2）随基础刚度提高、圆心角增大，涵顶及两涵之间填土沉降均减小，涵顶土压力增大，基础刚度提高将导致管涵径向土压力集中，填土、基础和管涵三者的接触点为最不利位置.

3）双孔钢波纹管涵在填土荷载作用下处于非对称受力状态，相邻管涵变形挤压涵间土体，导致靠近相邻管涵一侧水平轴线附近径向土压力大于另一侧.

4）无基础管涵沉降大，刚性基础易引起应力集中，圆心角较大且具有良好的变形协调能力的柔性基础，使管涵处于环形均匀受压状态，防止管涵发生失稳破坏，是较为理想的基础选型.