考虑乘客有限理性的城轨列车组合式停站方案优化研究

成琳娜，朱昌锋，王学贵，孙元广，方劲皓，王 傑

（1.兰州交通大学 交通运输学院，兰州 730070；2.五邑大学 轨道交通学院，广东 江门 529000；3.中铁第一勘察设计院集团有限公司，西安 710043；4.广州地铁设计研究院股份有限公司，广州 510010）

停站方案是城市轨道交通运营计划的重要组成部分.为了提高服务质量，城市轨道交通运营企业开始探索组合式停站方案.然而，乘客出行选择行为直接影响着城市轨道交通停站方案的优化，因此，如何从乘客有限理性的角度研究城市轨道交通停站方案具有重要的现实意义.

近年来，有关学者就城市轨道交通停站方案开展了相关研究.蔡芸等［1］通过考虑客流的不确定性，建立了基于机会约束规划的列车停站方案优化模型；段凌林等［2］在考虑越行站设置的前提下，提出了以优化乘客出行时间的快慢车停站方案模型；蒋琦玮等［3］通过引入灰色变权聚类法，构建了基于车站等级限制的快慢车停站优化模型；孙元广等［4］研究了快慢车开行方案的设计与评价方法.上述研究的前提假设均是乘客出行选择行为是在完全理性的状态下进行的.

但是，乘客在出行过程中的选择行为受到主观及客观的多方面因素影响，很难做到在完全理性下进行乘车选择［5］.基于此，姚恩建等［6］深入探讨了理性决策和固有选择偏好对出行方式选择的影响；Zhao等［7］分析了乘客的有限理性选择行为，研究了有限理性用户平衡状态的性质；徐红利等［8］指出如果乘客感知到实际出行成本接近经验出行成本时，不会更换原有出行方式，反之则会进行调整.

既有研究较少关注乘客出行选择的有限理性特征对停站方案的影响，部分学者也尝试研究有限理性条件下的城市轨道交通停站方案，但仅研究了单参考点条件下的停站方案.基于此，本文通过引入前景理论，提出有限理性条件下基于出行时间和拥挤费用双参考点的乘客出行选择决策理论，以出行时间前景值和拥挤费用前景值最大化为目标，构建考虑乘客有限理性的城市轨道交通组合式停站方案优化模型及其求解算法.

1 乘客有限理性选择行为分析

假设站站停方案、组合式停站方案所需的出行时间分别为Tq、Ts，拥挤费用分别为θq、θs.以出行时间、拥挤费用为“双参考点”，通过Tq与Ts、θq与θs的对比即可获得收益的乘车选择.由此，乘客做出某种乘车选择行为时，会出现两个可能的结果：

1）当Ts≤Tq或θs≤θq时，该选择所产生的实际成本不大于预期成本，获得相对收益.

2）当Ts＞Tq或θs＞θq时，该选择所产生的实际成本大于预期成本，产生相对损失.

基于此，构建有限理性条件下乘客出行时间价值函数和拥挤费用价值函数，即：

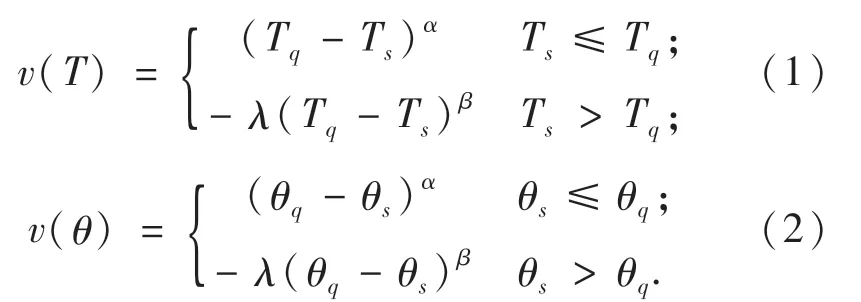
式中：α为收益敏感系数；β为损失敏感系数；λ为损失规避系数.三个参数共同描述乘客选择行为中的有限理性特征，将其定义为行为参数.出行时间价值函数、拥挤费用价值函数如图1所示.

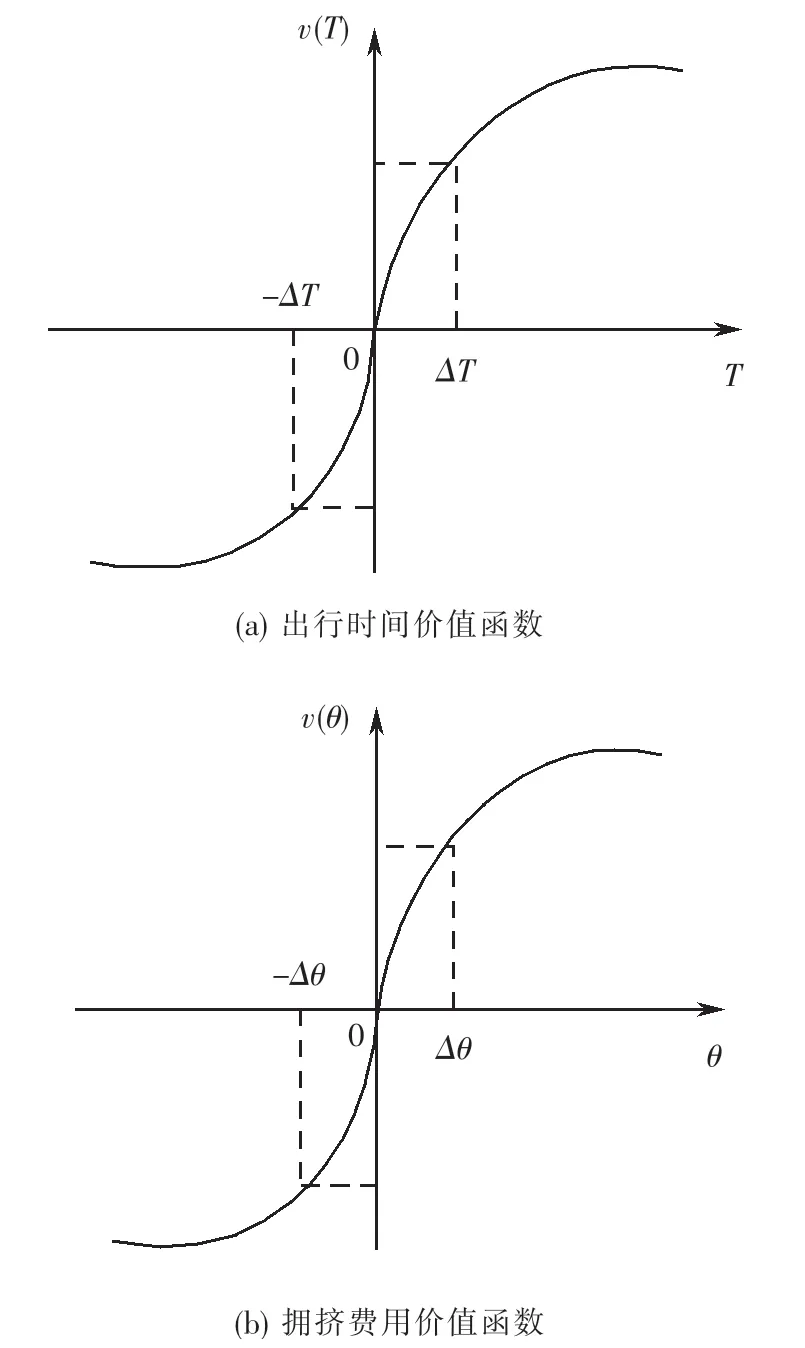
图1 价值函数Fig.1 Value function

图1分别以凹函数与凸函数描述了收益和损失状况.其中，ΔT、Δθ为获得区域，表示乘客所选停站方案相比站站停方案能够获得出行时间的节省或拥挤费用的降低，即Tq、θq不大于Ts、θs；-ΔT、-Δθ为损失区域，表示乘客所选停站方案相比站站停方案而言未能获得出行时间的节省或拥挤费用的降低，即乘客的心理预期参考值Tq、θq大于Ts、θs.

同时，有限理性条件下乘客对出行预期进行主观判断，进而以某种主观概率做出不同的乘车选择行为，由此构建有限理性条件下乘客出行时间概率权重函数和拥挤费用概率权重函数，即：

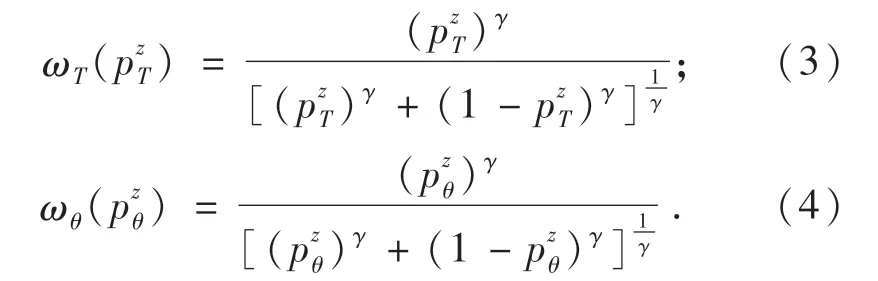
式中：pzT和pzθ为事件发生的主观概率；γ为主观概率函数的曲率.出行时间概率权重函数、拥挤费用概率权重函数如图2所示.

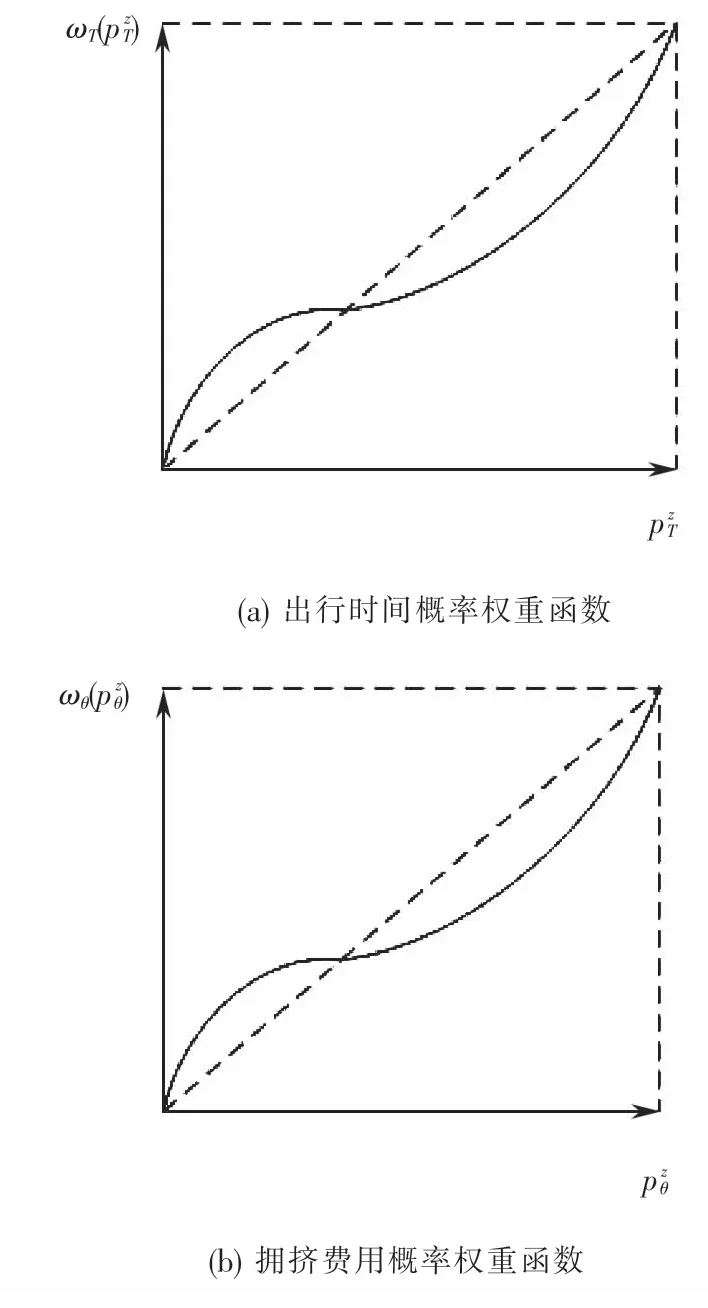
图2 概率权重函数Fig.2 Probability weight function

图2揭示了乘客会根据不同事件结果出现的概率进行主观判断，反映出乘客可能会更加重视小概率事件的选择倾向.

1）价值函数

乘客出行时间变化量包括三个部分：在途时间变化量、候车等待时间变化量及换乘等待时间变化量，即：

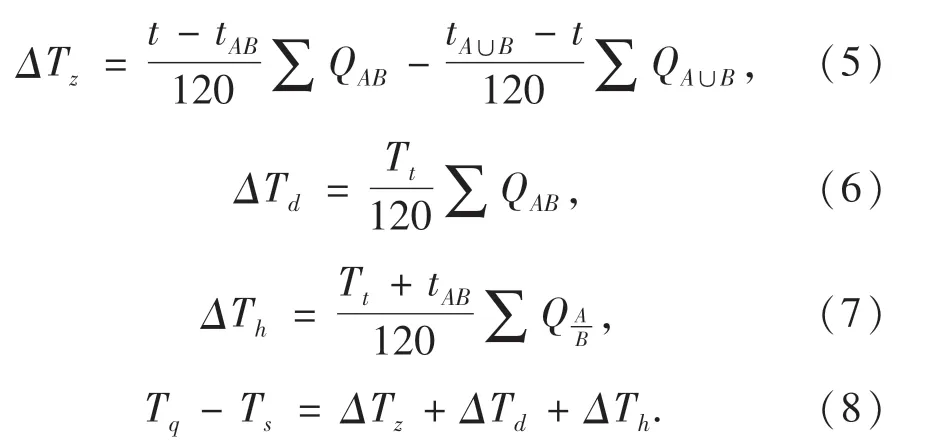
式中：ΔTz为组合式停站方案较站站停方案的在途时间变化量；ΔTd为组合式停站方案较站站停方案的候车等待时间变化量；ΔTh为组合式停站方案较站站停方案的换乘等待时间变化量；t为站站停方案下列车平均发车间隔；tAB为组合式停站方案下相邻开行LA类列车和LB类列车的时间间隔；tA∪B为组合式停站方案下相邻开行的两列LA类列车或相邻开行的两列LB类列车的时间间隔；Tt为列车停站引起的时间损失；∑QAB为SAB类车站间客流量；∑QA∪B为在SA类、SB类车站上车的客流量与在SAB类车站上车而在SA类或SB类车站下车的客流量之和；∑QA/B为LA类列车和LB类列车在SAB类车站的换乘客流量之和，各类客流量计算可参考文献［9］；S=｛Si|i=1，2，…，n｝为车站集合；SA、SB、SAB为车站的三个类别，且S=SA∪SB∪SAB；L=｛Lj|j=1，2，…，m｝为开行的列车集合；LA、LB为开行列车的两个类别，且有L=LA∪LB，LA类列车停靠于SA类及SAB类车站，LB类列车停靠于SB类车站及SAB类车站.

本文以列车到站时的满载率来计算拥挤费用，即：

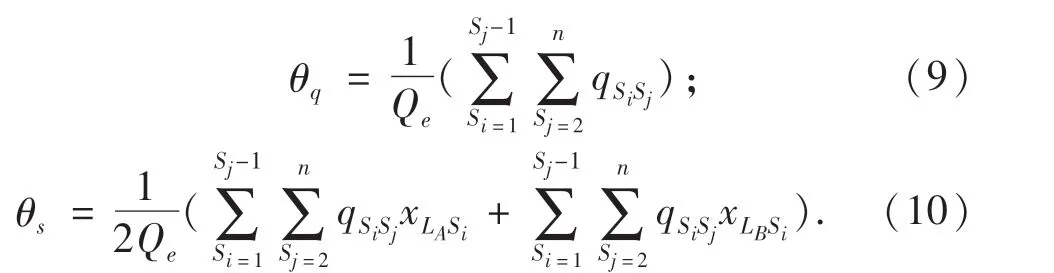
式中：xLASi和xLBSi为0-1变量，xLASi=xLBSi=1表示LA、LB类列车在车站Si停车，xLASi=xLASi=0表示不停车；Q=｛qSiSj|Si，Sj∈S｝为各车站间客流OD集合；Qe为列车的额定载客量.

2）概率权重函数

假设出行时间近似服从正态分布［10］，即T～N（E（T），σ2），则乘客选择第z种停站方案的出行时间主观概率pzT为

运用Si站客流量与区段总客流量的比值计算乘客选择第z种停站方案的拥挤费用主观概率pzθ为

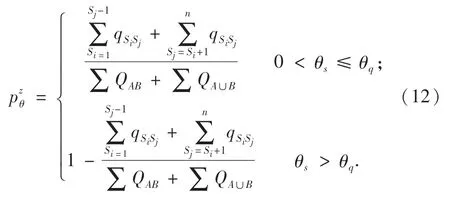
基于上述分析，可以得出出行时间前景值vzT和拥挤费用前景值vzθ，即：

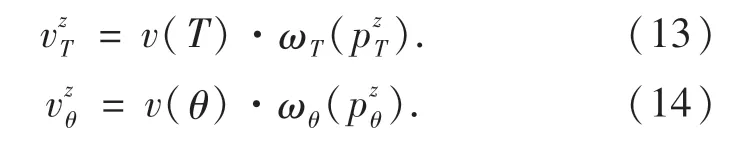
2 模型建立

本文以出行时间和拥挤费用为双参考点，通过构建价值函数和概率权重函数，可得出相应的前景值.前景值越大，乘客乘车选择行为的获益越多.由此构建出考虑乘客有限理性的城市轨道交通组合式停站方案优化模型.

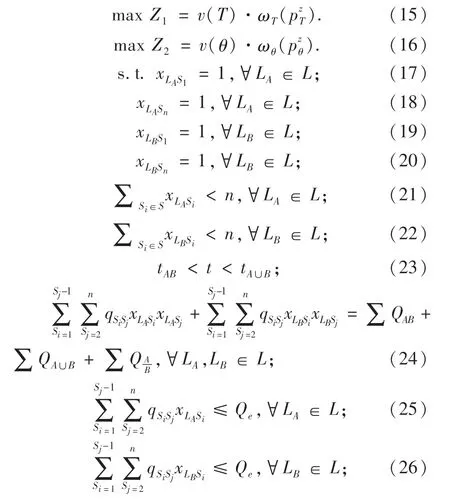
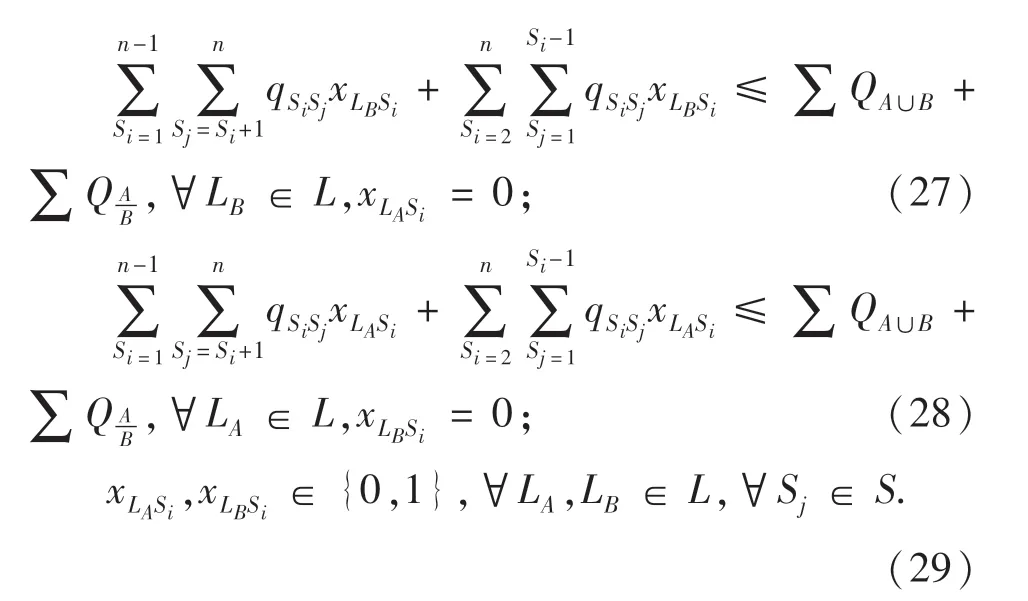
式（15）和式（16）分别为最大化出行时间前景值和拥挤费用前景值.式（17）至式（20）为运行起讫点约束，各类列车在起点和终点车站均需停车；式（21）和式（22）为停站次数约束，各类列车运行一次的总停站次数小于线路车站总数；式（23）为列车发车时间间隔约束；式（24）为客流约束，列车客流人数与线路客流需求总量一致；式（25）为列车定员约束，列车定员数不小于乘坐同一列车的乘客数；式（27）和式（28）为列车服务能力约束，当其中一类列车在某站不停车时，该站乘客应在一次候车过程中能够得到服务；式（29）为变量取值约束.

3 模型求解

针对本文模型有多个优化目标且解空间较大的特点，提出多目标优化的改进遗传算法对模型进行求解，即带精英策略的非支配排序遗传算法［11-13］.

1）编码和解码

采用0-1实数编码，染色体长度n对应车站总数，基因座是线路的站序，基因为表示列车是否停站的变量，0表示列车在该站不停车，1表示列车在该站停车.编码方案如图3所示.

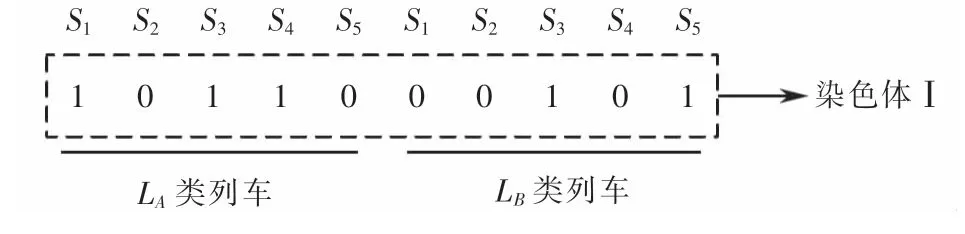
图3 城市轨道交通停站编码方案Fig.3 Coding scheme of stop plan for urban rail transit

2）适应度函数

以出行时间前景值vzT和拥挤费用前景值vzθ为适应度函数，计算每种停站方案的适应度值，淘汰其小于0的停站方案，并确定其余停站方案的crank值，从而进行快速非支配排序.操作过程如图4所示.

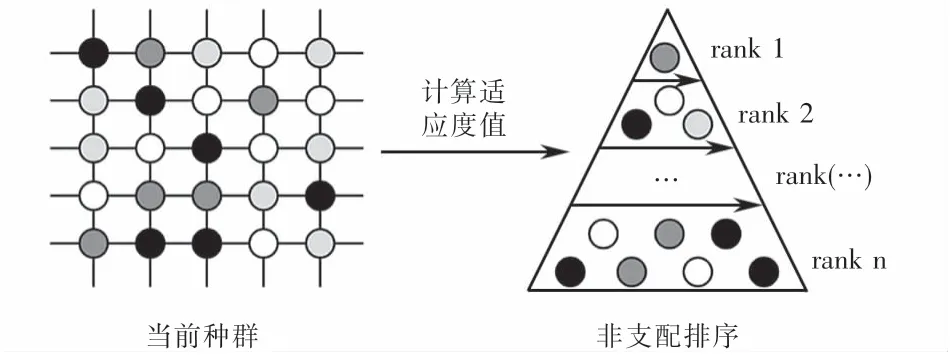
图4 快速非支配排序Fig.4 Fast non-dominated sorting

在此基础上，为了使Pareto前沿中的非支配解均匀分布，形成父代种群Pc，采用拥挤度算法作为适应度值共享方法，以拥挤距离cd作为拥挤度的判定标准，即：

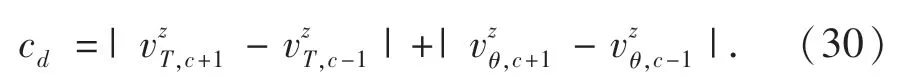
式中：vzT，c+1，vzT，c-1和vzθ，c+1，vzθ，c-1分别为在目标vzT（cz）和vzθ（cz）上的与个体c相邻的两个个体的适应度函数值.

3）交叉及变异算子

根据父代种群Pc中非支配次序关系和拥挤度值，通过锦标赛法选择个体进行多点交叉和基本位变异操作，保留精英个体产生子代种群Qc.交叉及变异算子如图5所示.

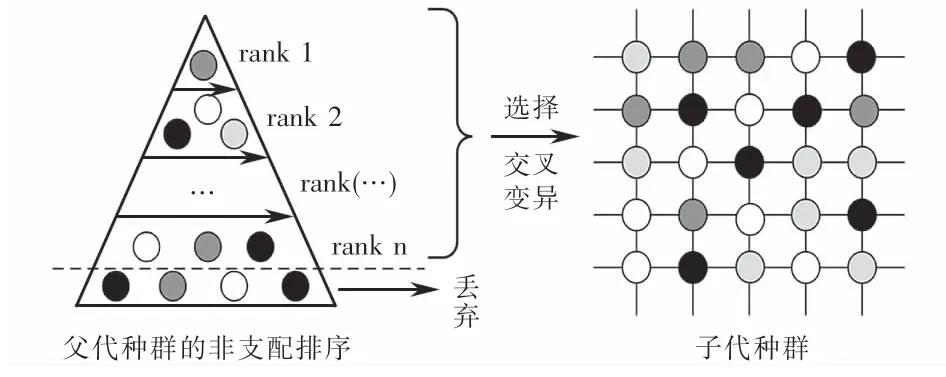
图5 产生子代种群Fig.5 Offspring population

4）选择算子

为了防止有效解丢失，确保父代中的优良个体保留到下一代，运用精英策略选择出适应度值较优的个体.精英选择算子如图6所示.

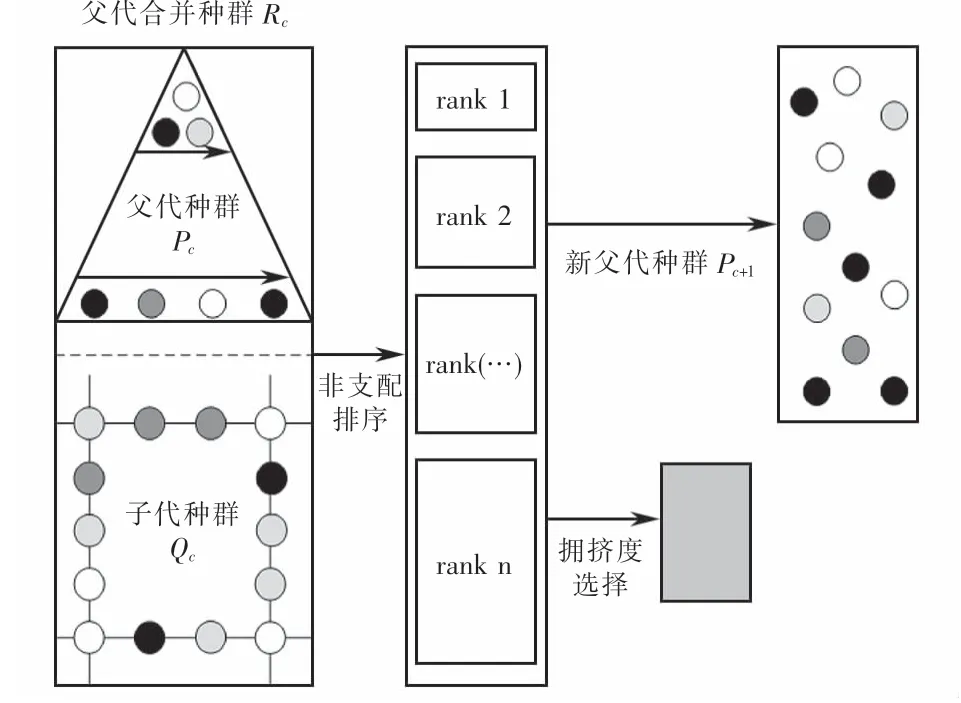
图6 精英选择算子Fig.6 Elite selection operator

5）迭代检验

重复上述操作，产生新的子代种群Qc+1，若满足停止条件，保存Pareto前沿的非支配解集.

算法流程如图7所示.

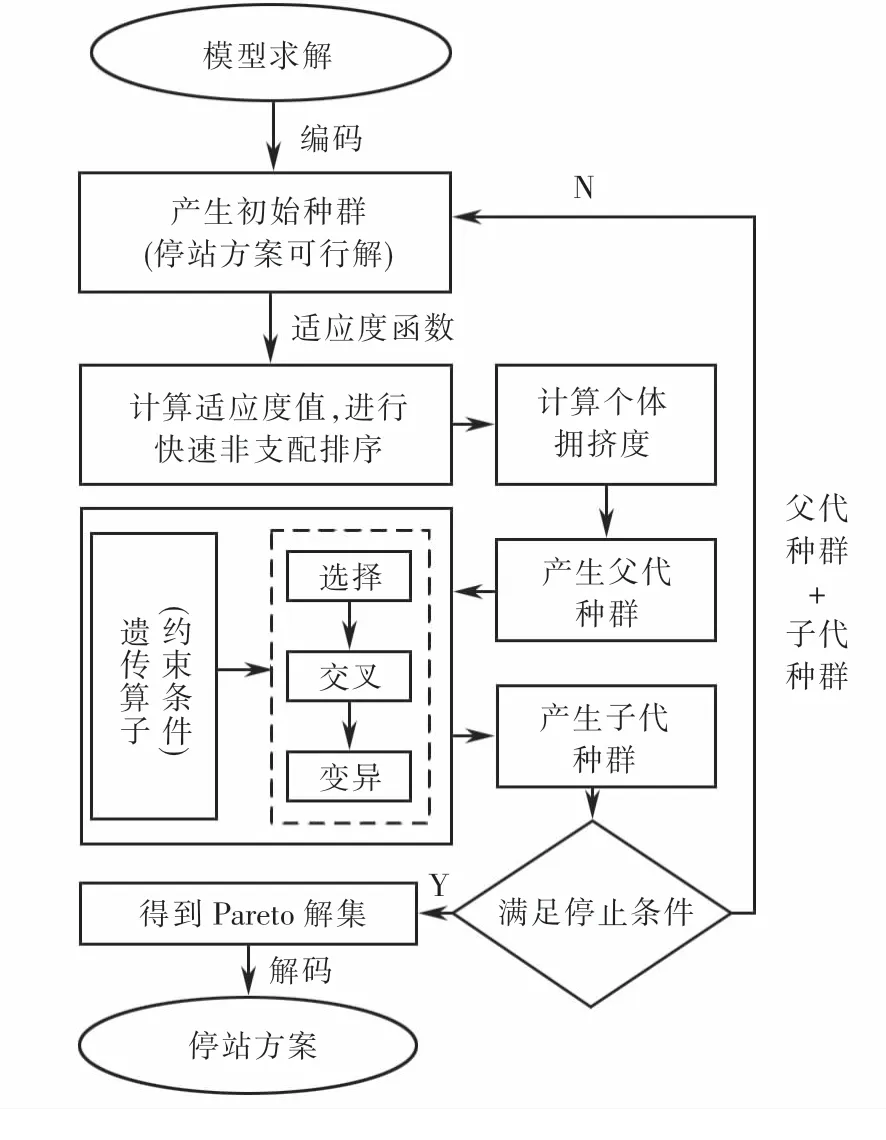
图7 算法求解流程Fig.7 Solving process of algorithm

4 实例分析

本文以广州地铁14号线为例，该线路共设13座车站（编号1～13），列车采用8节编组，车辆定员240人，同类列车与不同类列车的最小追踪间隔时间分别为2.5 min、10 min，采用工作日非高峰客流数据对模型进行验证.

问题求解过程中，迭代次数G为400，种群大小N取50，交叉概率pc取0.8，变异概率pm取0.01.前景理论参数α=β=0.88，λ=2.25，γ收益时取0.61，损失时取0.69［14］.

运用Matlab R2020b进行优化求解，当算法迭代约160次时，前景值趋于静止状态，计算得到三组Pareto解，分别对应于三种组合式停站方案，各方案性能对比分析如表1所列.

由表1可知，三个组合式停站方案虽然都增加了车站等候时间和换乘等候时间，但是都较显著减少了在途时间，因此均能够获得不同程度的总出行时间节省，分别节省了18 min、22 min和16 min.而且均能够在一定程度上降低拥挤费用，分别降低了5.5%、7.9%和10.9%.

表1 各方案性能对比分析Tab.1 Comparative performance analysis of each scheme

同时可知，vzT和vzθ呈现出负相关变化.方案Ⅰ的vzT和vzθ均处于计算结果中的次优状态，两类列车的拥挤均衡性能够得到一定程度的改善，并且乘客能够获得出行时间的节省，对于同等注重出行时间和乘车舒适度的乘客而言，该方案是最佳选择.方案Ⅱ的vzT最大，意味着乘客节省的出行时间最多，但此方案的vzθ最小，说明两类列车的拥挤均衡性较差，在不同时段可能存在着运能不足或运能浪费的情况，对于更加注重出行时间的乘客而言，该方案是最佳选择.方案Ⅲ的vzθ最大，意味着两类列车的拥挤均衡性最优，运用车的使用均衡性较好，能够更充分地利用列车使用成本，但此方案的vzT最小，说明乘客能够获得的出行时间节省最少，对于更加注重乘车舒服度的乘客而言，该方案是最佳选择.

优化后的组合式停站方案示意图如图8所示，城市轨道交通运营企业可综合考虑该线路客流出行情况和运营成本控制需求等，根据实际需要采用具有针对性的列车停站方案.

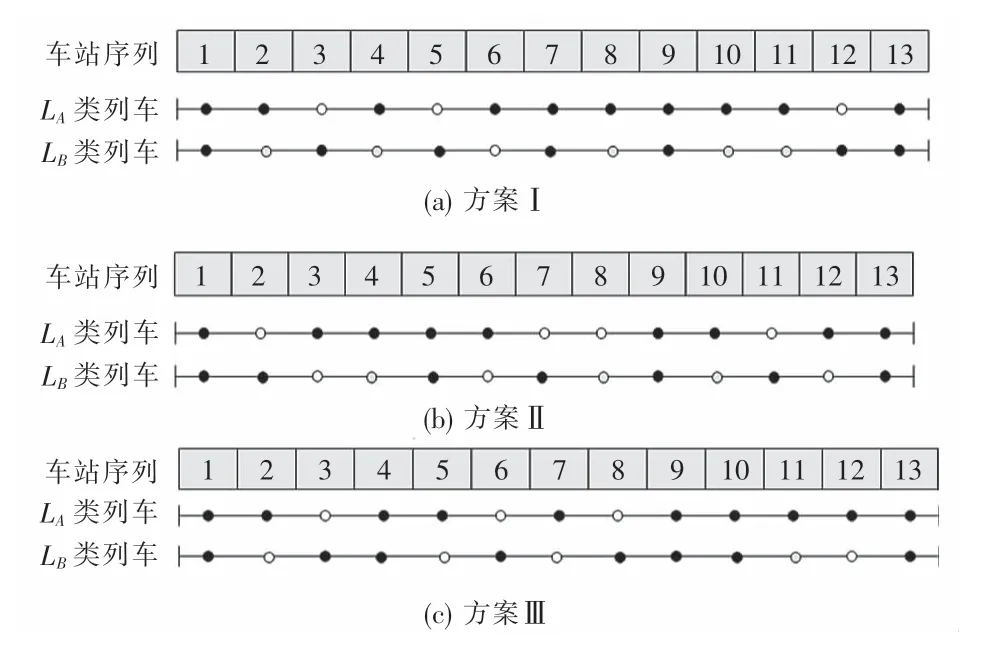
图8 组合式停站方案示意图Fig.8 Schematic diagram of skip-stop scheme

考虑到不同程度的有限理性对乘客选择行为结果的影响，即行为参数对前景值的影响.Schwanen等［15］调查发现1.09≤α≤1.10、1.09≤β≤1.10、1.27≤λ≤1.37.Avineri等［16］研究发现各时段的λ值存在差异：早高峰为0.76；晚高峰为1.62；其它时段为1.28.基于此，本文以组合式停站方案Ⅰ为例，对α、β、λ等行为参数的取值进行扰动分析，得到前景值变化灵敏度如图9～12所示.

图9和图10反映了收益敏感系数α、损失敏感系数β对方案Ⅰ出行时间前景值vzT和拥挤费用前景值vzθ影响的对比分析.结果表明，vzθ和vzT几乎不受β的影响；vzT随着α的增加表现出稳定的增长趋势，当α＞0.55时方案Ⅰ开始能够获得出行时间的节省；vzθ随着α的增加表现出程度不定的起伏波动，在α≈0.85时出现大幅度增加，表明此时两类列车的拥挤均衡性开始得到明显改善.说明乘客在乘车选择过程中，对能够获得的收益更加敏感.

图9 α、β对方案ⅠvzT的影响Fig.9 Influence ofαandβon vzT of schemeⅠ

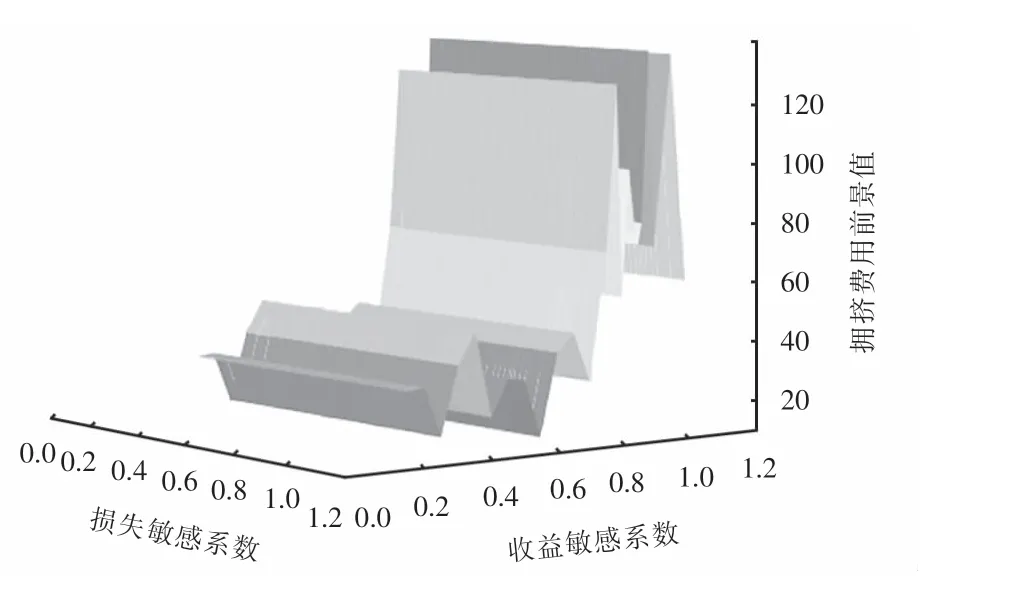
图10 α、β对方案Ⅰvzθ的影响Fig.10 Influence ofαandβon vzθof schemeⅠ

图11和图12反映了损失敏感系数β、损失规避系数λ对方案Ⅰ出行时间前景值vzT和拥挤费用前景值vzθ影响的对比分析.结果表明，vzθ和vzT几乎不受β的影响；vzT随着λ的增加表现出稳定的增长趋势，0.55＜λ＜1.35范围内vzT具有较快的增长速率，λ＞1.35时增长速率开始减缓，且λ＞1.65时方案Ⅰ开始能够获得出行时间的节省；vzθ随着λ的增加表现出程度不定的起伏波动，在λ≈1.55时出现大幅度增加，表明此时两类列车的拥挤均衡性开始得到明显改善.说明乘客虽然对乘车过程中产生的损失较为不敏感，但对可能面临的损失仍会表现出强烈的规避心理.

图11 β、λ对方案ⅠvzT的影响Fig.11 Influence ofβandλon vzT of schemeⅠ

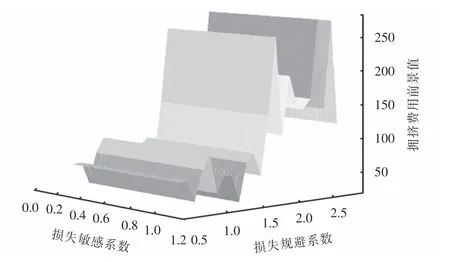
图12 β、λ对方案Ⅰvzθ的影响Fig.12 Influence ofβandλon vzθof schemeⅠ

5 结论

根据乘客选择行为的有限理性特征，提出考虑乘客有限理性的城市轨道交通组合式停站方案优化模型，可以从乘客所获得的出行时间“收益”和产生的拥挤费用“损失”等方面进行选择行为分析应用，优化结果可以用于客流需求动态条件下城市轨道交通停站方案适应性调整.

实例分析结果表明，本文设计的优化模型与算法能在较短时间内获得可行解，得到的三种组合式停站方案将乘客出行时间平均减少了18.6 min、拥挤费用平均减少了8.1%，具有更好的客流适应性.通过行为参数的灵敏度分析可知，收益敏感系数和损失规避系数的变化会使得出行时间前景值和拥挤费用前景值出现明显波动，从而对停站方案优化结果产生影响；而出行损失敏感系数的变化所产生的影响较为微弱.

下一步研究可深入探讨行为参数变化对停站方案优化的影响，进一步改进前景理论在城市轨道交通停站方案优化问题中的应用效果.同时，对该方法的优化目标进行拓展研究后，将适用于不同优化视角下停站方案的调整.