基于边缘特征的图神经网络架构搜索

周 鹏，杨 军*，2

（1.兰州交通大学 电子与信息工程学院，兰州 730070；2.兰州交通大学 测绘与地理信息学院，兰州 730070）

以AlexNet［1］，GoogleNet［2］和RCNN［3］为代表的 人工设计神经网络在图像分类、分割和目标检测等计算机视觉领域取得了很大成功.人工设计网络架构需要进行不断重复实验，消耗了大量的人力和计算资源，且依赖专家经验，专家需要重新设计算法适应新任务.因此，通过算法自动搜索出优秀的网络架构逐渐成为该领域的研究热点.神经网络架构搜索（neural architecture search，NAS）旨在预定义的搜索空间中由搜索策略找到针对特定数据集的候选网络架构，通过性能评估策略对候选架构进行评估，将评估结果反馈到搜索策略，再由搜索算法调整搜索策略，通过不断重复搜索过程，直到发现最优的神经网络架构.NAS在计算机视觉领域的表现已经达到，甚至超过人工设计的深度神经网络，但仍需要耗费巨大的计算资源评估网络架构.可微分架构搜索（differentiable architecture search，DARTS）［4］通过连续松弛化原有离散搜索策略，利用梯度下降法优化网络架构，但离散化得到的子网与超网之间存在性能差距，子网需要重新训练，导致搜索结果不稳定.文献［5］对DARTS算法进行了改进，所提出的sharpDARTS引入余弦幂次退火算法对学习率进行更新，借助正则化方法纠正DARTS算法中的性能差距，降低了基于梯度算法消耗内存过大的问题；文献［6］提出渐进式可微分结构搜索（progressive differentiable architecture search，P-DARTS）算法，使用搜索空间正则化来提高搜索的稳定性，并逐步增加网络层数以减少内存消耗；文献［7］提出连续贪婪策略搜索算法（sequential greedy architecture search，SGAS），优化了搜索过程和验证过程准确率差异的问题.

近年来，研究者将NAS应用于图机器学习领域，称为图神经网络架构搜索（graph neural architecture search，GNAS）.文献［8］首次用NAS算法来解决图神经网络（graph neural network，GNN）中的架构搜索，实现了基于强化学习的图神经架构自动设计；文献［9］提出边缘特征图注意力网络，将图神经网络的使用扩展到具有节点和边缘特征的任务，但该方法缺乏不同的更新函数来计算边缘特征；NENN由节点级注意力层和边缘级注意力层构建网络模型，交替地将2种注意力层堆叠，并在相应的级别上学习节点和边缘的特征［10］；文献［11］提出索引边缘几何卷积神经网络模型，将不同层的输出特征映射并进行索引跳跃连接，使局部特征信息损失进一步降低.图神经网络的广泛应用，使得基于复杂图结构数据的任务，如点云分类、社会关系网络分析、专家推荐系统及化学分子性质预测等问题得以高效解决，然而，GNN的可扩展性会导致计算成本增加，并随着层级的深入呈指数增长，在对点云分类等大规模计算时挑战巨大.

综上所述，目前图神经网络架构搜索注重研究实体的特征信息，忽略了边缘上的潜在高阶信息与多层次关系特征之间的依赖，设计高效提取边缘特征的图神经网络架构搜索空间与搜索算法，依然是一个需要研究的问题.本文提出边缘特征图神经网络架构搜索（edge feature graph neural architecture search，EFGNAS）的方法，首先，在搜索空间中设计用于提取边缘特征的候选操作，将边缘与实体视为等价体，利用双层优化方法同步更新实体和边缘的高阶信息，采用边缘卷积同步提取局部和全局边缘特征，以提高图神经网络架构的搜索性能；其次，设计基于边缘特征的图神经网络架构搜索空间，用于实体和边缘的更新；最后，提出基于边缘特征提取的图神经网络搜索算法，采用双层优化方法实现三维点云模型的分类.

1 搜索空间与搜索算法设计

本文采用边缘卷积的方法提取三维点云特征，通过边缘特征提取的方法对NAS的搜索空间进行优化设计，使用分组卷积提升搜索效率，并设计基于双层优化的图神经架构搜索算法.

1.1 点云特征提取

首先，计算全局点云特征.在三维点云中任选一点，计算以该点为中心的球形邻域，通过迭代提取全局点云特征.其次，计算局部点云特征.采用边缘卷积构造局部邻域图，在逐层卷积相邻边缘的过程中，输出每一层在新特征空间的点云结构图，得到一个新的局部区域；以中心点、中心点与邻域点间距离为参数，计算点云局部特征.最后，由非对称边缘函数根据全局信息与局部信息计算三维点云边缘特征.

设G=（v，ε）为点云结构图，其中：v=｛v1，v2，…，vn｝表示点；ε表示边.G中包含每个点的自循环，即每个点存在指向自身的边.给定∀vi，构造以vi为中心的球形邻域N（vi），

其中：r表示邻域半径.当得到若干邻域后，计算中心点vi的边缘特征的输出v′i，

其中：hθ（vi，vj）表示边缘特征；hθ为包含可学习参数θ的非线性边缘函数；Φ表示对边缘特征进行通道对称聚合.边缘函数hθ与聚合操作Φ决定边缘特征的输出.针对三维点云特征提取，分为以下3种情况：

1）当hθ（vi，vj）=hθ（vi）时，表示对全局点云进行特征提取，不考虑局部邻域结构.这种类型的特征提取方式在PointNet［12］中被使用，因此，可以看作是边缘特征提取的一种特殊形式.

2）当hθ（vi，vj）=hθ（vj-vi）时，表示仅对局部点云进行特征提取，而不考虑全局结构.

3）当hθ（vi，vj）=hθ（vi，vj-vi）时，表示既考虑全局点云特征提取，又考虑局部邻域信息，是本文采取的特征提取方式.

边缘特征融合点间局部关系和全局信息，在得到若干个边缘特征后，进行最大池化操作，得到该局部区域的单一特征，以这种方式进行多层卷积叠加，逐层提取并整合局部特征信息.

1.2 搜索空间设计

GNN可表示为使用消息传递机制工作的网络，其每一层有一个聚合函数g和一个基于神经网络的更新函数u.在图G中，给定∀vs表示序号为s的节点，χt-1s表示节点vs在时间步长t-1的特征，消息向量mts是由节点vs的邻域点集Ns通过聚合函数计算得到，节点的特征χts由更新函数u和消息向量mts计算得到，如式（3）所示.

通过这种消息传递方式，在T层的GNN网络中，消息以T个时间步长进行传递.该方法在处理结构化的二维图像和序列化的信息等固定格式数据时非常有效，而对于数据量大、邻域数据集多的大型图结构，处理的效率和稳定性较低.为提高GNN在三维点云分类中的性能，本文采用网络架构搜索的方式构建分类网络.网络架构搜索是一个逐步求精的过程，通过丢弃特征提取不佳的候选操作得到最优的网络架构.

采用图神经网络的目的是寻找一种单元作为最终架构的构建模块，每个单元是由M个节点的有序序列组成的有向无环图（directed acyclic graph，DAG），每个节点之间的信息通过节点间的边传递，每条边包含若干候选操作和相应的网络架构参数α，搜索空间中候选操作选择流程如图1所示.通常采用梯度下降的方法同时优化网络架构参数α和权重参数ω，对α的优化可提高最终训练的准确率，对ω的优化可以加快训练准确率的提升，图神经网络架构搜索的最小单位称为搜索单元（cell）.图1（a）表示搜索算法需从搜索空间中选择候选操作；图1（b）中，搜索空间中有预先设计的诸多候选操作，由搜索策略组合不同的候选操作，再由评估策略对组合后的网络架构进行性能评估，保留对性能提升贡献大的候选操作，最终得到目标架构，如图1（c）所示.

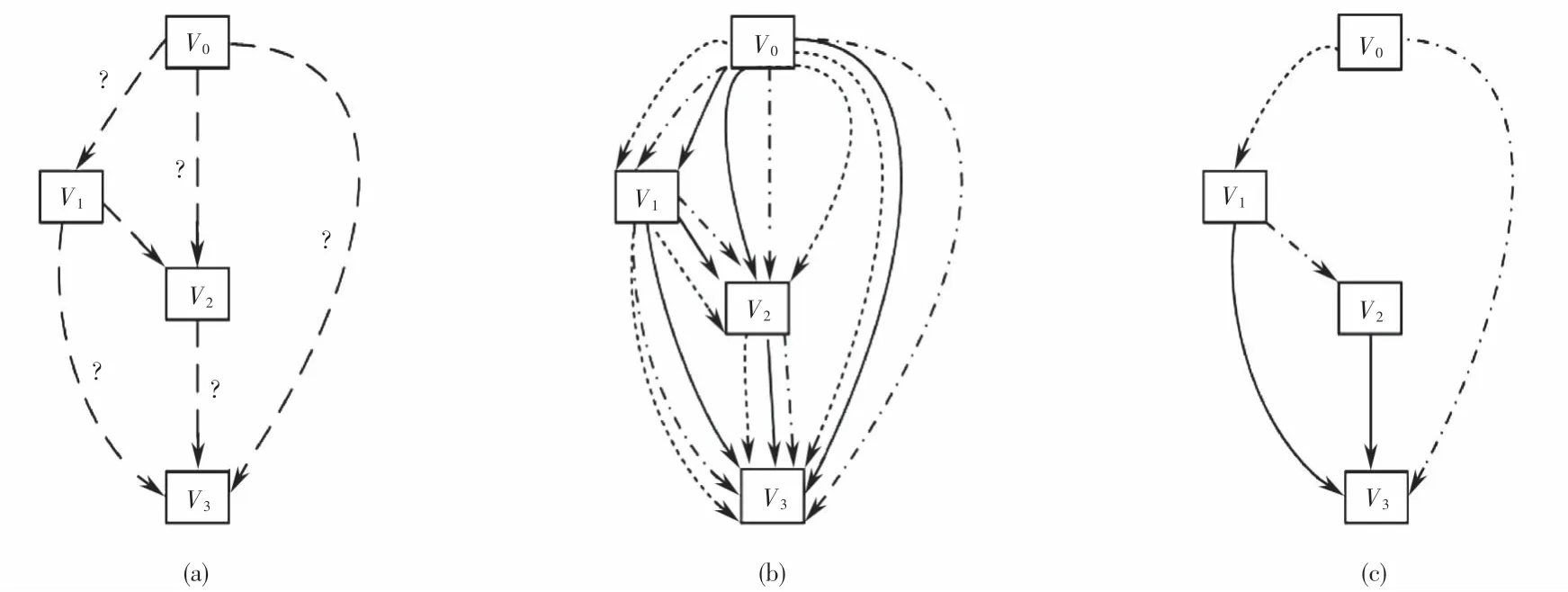
图1 基于有向无环图的神经网络架构搜索决策过程Fig.1 Decision process of neural architecture search based on directed acyclic graph

在搜索空间中，采用的候选操作有rel_sage［7］，edge_conv［13］，mr_conv［14］，gat［15］，semi_gcn［16］，gin［17］，sage［18］，conv-1×1，skip-connect，EdgeConvDiff，EdgeGroupConv，EdgeGroupConvDiff，其中：conv-1×1是一个基本卷积操作；skip-connect表示跳跃连接操作；EdgeConvDiff，EdgeGroupConv与EdgeGroupConvDiff为本文新设计的候选操作，EdgeConvDiff为采用边缘卷积提取三维点云全局特征，EdgeGroupConv为采用边缘卷积提取三维点云局部特征，EdgeGroupConvDiff为采用边缘卷积提取三维点云全局与局部特征，EdgeGroupConv与EdgeGroupConvDiff候选操作中引入了分组卷积和通道洗牌操作.

DAG图中的每一个节点代表一个特征图，用Vi表示，i为节点的序号，特征图之间的连线表示候选操作，每一条连线都存在与相连节点相关的混合操作O（i，j），这些操作通过节点之间的关系特征E（i，j）将信息从Vi传递到Vj，如图1中，V0为输入，V3为输出，V1，V2为中间节点，中间节点既是输入节点，又是输出节点，并携带上一步的状态信息z，由前驱节点计算得到

其中：1≤j≤M.初始节点V0表示输入一个实体信息，中间节点由输入节点Vi、关系特征E（i，j）及状态z经过混合操作O进行加权计算.

综上所述，本文针对三维点云分类设计搜索空间.如图2（a）所示，在搜索空间中，点云特征的提取基于图卷积网络，vi为中心点，vik表示vi的邻域，eik为vi和vik构成的边（k=1，2，…，n）；图2（b）表示采用边缘卷积的方法提取点云全局和局部特征，hθ为非线性边缘函数.由于点云模型具有无序性、稀疏性、数据有限性等特点，使采用图卷积网络的处理效率不高.因此，为了提高点云的分类效率，本文采用组卷积方式对输入的特征图进行分组，如图2（c）所示，共分为2组，每组分别卷积，再由通道洗牌操作促使特征信息跨特征通道传递；组卷积从不同组中获取输入数据，输入和输出通道完全相关；对于由前一组生成的特征映射，将每一组内的通道划分为不同的子组，然后把不同的子组提供给下一层，这一过程由通道洗牌操作完成.通道洗牌是可微的，可以嵌入到网络架构进行端到端训练，这使得构建具有多组卷积层的网络架构成为可能.

1.3 基于双层优化的搜索算法

搜索空间A由不同的候选操作构成，旨在处理复杂的图结构数据，传递不同类型的神经网络消息.为提高GNN处理三维点云的效率和稳定性，本文采用基于双层优化的自动架构搜索算法.GNAS可定义为一个双层优化过程，在给定的图搜索空间A中找到一个最优的神经网络架构α*∈A，同时使验证损失函数Lval（·）的值最小.通过使训练损失函数Ltrain（·）最小化，得到与网络架构相关的可训练权重ω*，表示如下：

在DAG中，搜索算法根据预定义的选择策略，在每一次迭代决策过程中，选择一条边，然后更新权重参数ω，当架构参数α值最大时，选择对应的边，同时裁剪掉局部α值最小时对应的边；随着裁剪的执行，剩余的参数将形成一个新的子问题，并进行迭代求解；在最后的搜索过程中，可以获得一个独立的无需共享权重架构.算法步骤如下：首先，定义GNAS的架构参数为α，网络权重为ω，迭代次数为L，为抑制网络过拟合，提高网络的鲁棒性和泛化能力，本文引入正则化方法规范架构参数的优化过程，定义正则化系数λl和正则化项rl，l∈｛1，2，…，L｝，正则化项rl通过计算架构参数指数和的对数后，再计算其平均值得出，用pytorch语言表示为rl=torch.mean（torch.logsumexp（self.model._arch_parameters，dim=-1））；其次，计算▽ALval（ω，α）+λlrl，以逐步更新网络架构参数α，并且计算▽ωLtrain（ω，α），以逐步更新网络权重ω，如果当前的迭代过程是决策过程，则选择网络架构参数α值最大时对应的边，并在新选择的边上更新相关候选操作，再裁剪未被选中的网络架构参数α和权重参数ω；最后，根据选择到的候选操作组成目标架构.

2 仿真实验与结果分析

2.1 在ModelNet10数据集上的搜索实验

ModelNet［19］常用于三维模型分类，它包含ModelNet40和ModelNet10 2个数据集.ModelNet40含有40类12 311个CAD数据模型，其中：9 843个数据模型用于训练；2 468个数据模型用于测试.Model-Net10是ModelNet40的子集，包含10类，共4 899个CAD数据模型，其中：3 991个模型用于训练；908个模型用于测试.本文采用GNAS的网络架构搜索方法，在ModelNet10数据集上进行搜索，在Model-Net40数据集上进行测试.

2.1.1 搜索空间参数设置

搜索空间的主干网络由6个normal cell和2个reduction cell构成，其中：reduction cell位于网络1/3和2/3处，其余为normal cell.设置normal cell的卷积层步长为1，reduction cell的卷积层步长为2.共有12个候选操作，如1.2节所述.

2.1.2 训练参数设置

本文在ModelNet10数据集训练和验证，初始通道数设置为32个，采样点为1 024个，初始cell数设置为2个，迭代次数设置为50次，输入批量大小设置为32个，初始学习率的值为0.005，动量值为0.9，权重衰减值为3×10-4.采用随机梯度下降（stochastic gradient descent，SGD）优化模型权重.设置初始迭代9次之后开始做决策选择，每迭代7次做出一次搜索决策.由于硬件资源的局限性，批量值设置过大，会耗费更多的计算资源，达到相同准确率所需的迭代数量增多，同时梯度震荡严重，不利于收敛；批量值设置过小，不同批量计算时梯度方向变化过小，容易陷入局部极小值.本文采用批量值动态调整策略，当出现搜索决策时，将批量值设置为“批量值+当前迭代次数”，从仿真实验可以看出，该策略平均测试GPU时长为0.284 3 d，而消融实验中平均测试GPU时长为1.027 2 d，采用该策略的训练耗时大幅降低.

2.2 在ModelNet40数据集上的测试实验

本文在ModelNet10数据集上，通过6个不同子实验得到6个网络架构，分别命名为EFGNAS_1，EFGNAS_2，EFGNAS_3，EFGNAS_4，EFGNAS_5和EFGNAS_6.在ModelNet40数据集上测试，搜索出6个网络架构，得到三维点云分类的结果.将搜索的单元堆叠3次，采样点为1 024个，通道数设置为128个，评估过程迭代次数设置为250次，批量大小设置为32个.使用Adam优化模型权重，权重衰减值为1×10-4，学习率的值为0.001.测试结果见表1.

从表1可以看出：在ModelNet10数据集上训练时，网络收敛快，随着损失的稳步降低，训练准确率逐步上升，最高达到97.24%，而验证分类准确率最高为90.23%，测试分类准确率最高为93.42%.研究分类准确率与GPU时长、参数量的关系得知：在同样的迭代次数下，最优网络架构所对应的测试分类准确率与训练和测试所耗费的GPU时长、参数量没有直接的对应关系.

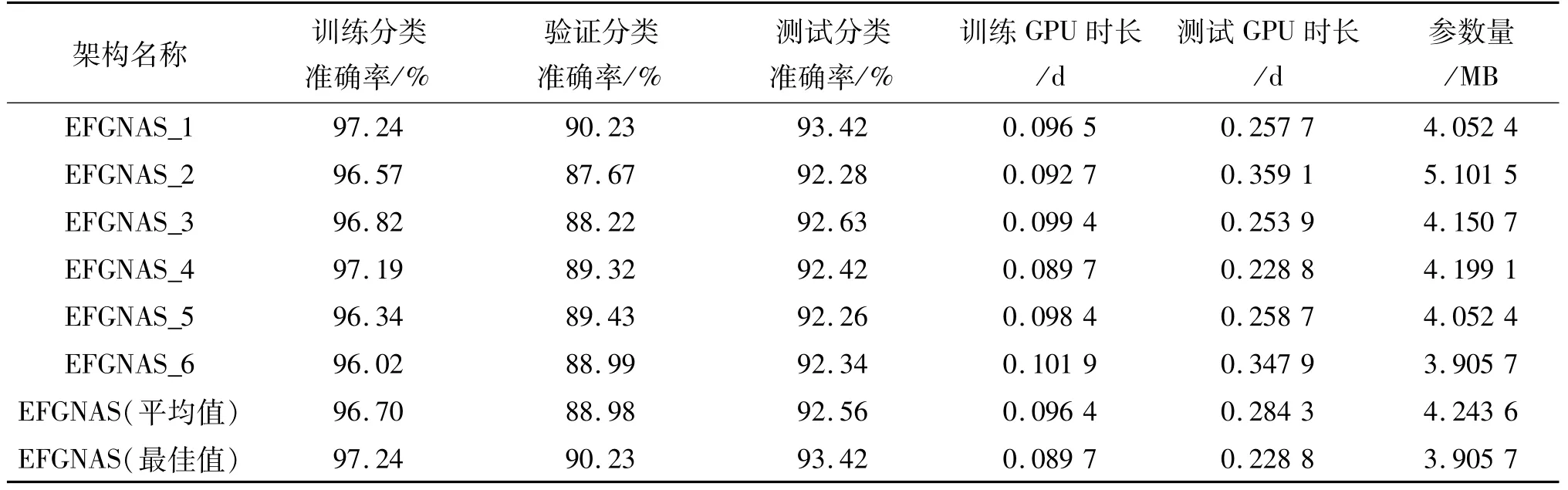
表1 EFGNAS在ModelNet数据集上的分类效果Tab.1 Classification accuracy of EFGNASon ModelNet

为了进一步说明本文算法的性能，图3给出了EFGNAS的分类准确率与迭代次数的关系曲线图.在图3（a）中，模型的分类准确稳步提升，从训练开始到第25次迭代，性能提升较快，在35～50次迭代中，前期表现较差的训练过程分类准确率提升较快，逐步接近最佳分类准确率；由图3（b）和图3（c）可知，在验证和测试过程中，前10次迭代的性能提升比较快，在11～15次迭代过程中，性能出现大幅下降，之后又出现逐步提升.可见，在数据量较小的ModelNet10数据集上，容易出现过拟合的情况，通过引入的正则化项后，在一定程度上抑制了过拟合的产生，保证了在小数据量模型时训练的正常进行.

图3 EFGNAS在训练、验证与测试中的分类准确率与迭代次数关系曲线图Fig.3 Plot of classification accuracy with iterations in training，validation and testing by EFGNAS

图4为搜索出来的6个网络架构的图形化表示，其中：c_｛k｝为所有中间节点的深度连接，表示当前网络架构的输出；c_｛k-1｝和c_｛k-2｝分别表示第k-1，k-2个网络架构的输出.从图4可以看出：搜索结果中均出现本文所设计的EdgeConvDiff，EdgeGroupConv与EdgeGroupConvDiff等候选操作；测试分类准确率前3位分别为图4（a）、图4（c）和图4（f）的网络结构，新设计的候选操均出现2次，在图4（d）中出现3次，但图4（d）所对应的网络架构测试分类准确率并不是最高，可见架构性能的优劣和整体架构中所有候选操作及其构成方式有很大关系.

图4 EFGNAS生成架构的图形化表示Fig.4 Gaphing of the searched architecture by EFGNAS

EFGNAS与人工设计的网络架构、自动搜索的架构在三维点云模型上的分类准确率、参数量和所需GPU时长对比结果见表2，其中：manual表示人工设计的网络架构.

由表2可知：本文方法EFGNAS（最佳值）与SGAS相比，参数量增加0.044 3 MB，所占用的GPU时长比SGAS减少0.031 2 d，分类准确率提升了1.42%，由于SGAS算法搜索空间中的候选操作没有考虑到分组卷积和边缘特征的提取，影响了分类准确率的提升；与RBNAS相比，本文方法EFGNAS（最佳值）的分类准确率提高了0.32%，参数量减少了0.204 3 MB，GPU时长增加了0.108 8 d，原因是RBNAS算法资源平衡型渐进式剪枝的思路存在对渐进系数的过分依赖；与NoisyDARTS相比，本文方法EFGNAS（最佳值）的分类准确率提高了0.52%，参数量减少了4.574 3 MB，GPU时长增加了0.118 8 d，原因是NoisyDARTS在候选操作中添加了噪声，使候选操作之间公平竞争，特别是对跳跃连接的过快增长起到了一定的抑制作用，但是与选择的噪声及特定的数据集密切相关，且泛化能力较弱；本文在SGAS的基础上，采用边缘卷积的方法提取了点云的全局特征与局部特征，同时，为降低引入图卷积导致计算成本的增加，采用分组卷积的方法提升了搜索效率，本算法的平均分类准确率EFGNAS（平均值）为92.56%，最佳分类准确率EFGNAS（最佳值）为93.42%，搜索到的最佳网络架构取得了较低的GPU运行时长和参数量，且分类准确率高于目前常见的人工设计和自动搜索的网络架构，说明采用边缘卷积的方法能提取更丰富的点云特征.

表2 本文方法与其他方法在三维模型分类上的比较Tab.2 Comparison with the proposed method with other methods in three-dimensional classification

2.3 消融实验

为进一步验证采用边缘特征提取的方法对分类准确率的影响，本文完成了未进行边缘特征提取的实验，实验名称为EFGNAS*.实验所得到的分类准确率、训练GPU时长、测试GPU时长和参数量见表3.从表1和表3可看出：EFGNAS（最佳值）测试分类准确率较EFGNAS*（最佳值）提高了1.12%，尤其在测试GPU时长方面，较EFGNAS*降低了74%，因此，本文算法有效提升了搜索效率，且在测试分类准确率有一定提升的前提下，网络参数量和GPU运行时长降低显著.

表3 EFGNAS*在ModelNet数据集上的分类效果Tab.3 Classification accuracy of EFGNAS*on ModelNet

图5为EFGNAS*在训练、验证与测试中的分类准确率与迭代次数关系曲线图.如图5（a）所示，EFGNAS*在训练过程中，分类准确率上升比较平稳，6次训练中，最高分类准确率为97.02%，比EFGNAS低0.22%，从开始训练到迭代10次，性能提升较快.其中：3次训练过程分类准确率较低，在迭代的中后期，虽然性能有一定提升，但仍与最高分类准确率存在差距，而EFGNAS前期性能提升较慢的训练过程在迭代的中后期提升较快，接近最高分类准确率.由图5（b）和图5（c）可知：EFGNAS*的验证分类准确率和测试分类准确率在刚开始到第10次迭代过程中准确率提升较快，之后出现大幅下降，且后期提升缓慢.对比图3（b）和图3（c）可知：本算法鲁棒性较强，能有效抑制过拟合，分类准确率上升平稳.

图5 EFGNAS*在训练、验证与测试中的分类准确率与迭代次数关系曲线图Fig.5 Plot of classification accuracy with iterations in training，validation and testing by EFGNAS*

表4对比了EFGNAS和EFGNAS*分类准确率的排序.

表4 2种不同网络模型在训练、验证和测试中分类准确率的排序Tab.4 Classification accuracy rank of two different network models in training，validation，and testing

将排序表示为肯德尔相关性系数时可以分析出不同排序的相关性.肯德尔相关系数又称和谐系数，是一个用来测量2个随机变量排序相关性的统计值，表示为

其中：c为所对比的2个序列中拥有一致性的元素对数；d表示序列中拥有不一致性的元素对数；n表示样本量表示所有样本两两组合的数量.一个肯德尔检验是一个无参数假设检验，它使用计算所得的相关系数去检验2个随机变量的统计依赖性.τ的取值范围为［-1，1］，当τ为1时，表示2个随机变量拥有一致的等级相关性；当τ为-1时，表示2个随机变量拥有完全相反的等级.理想的NAS算法应该具有较高的搜索-测试肯德尔相关性系数τ.

本实验对比EFGNAS和EFGNAS*的训练阶段、验证阶段和测试阶段的肯德尔相关系数.表5为EFGNAS和EFGNAS*分类准确率排序的肯德尔相关系数值，由训练阶段、验证阶段和测试阶段的分类准确率排名计算所得.从表5和式（6）可知：EFGNAS训练阶段与验证阶段分类准确率的τ值为0.333 3，EFGNAS*训练阶段与验证阶段分类准确率的τ值为0.200 0；EFGNAS训练阶段与测试阶段分类准确率的τ值为0.600 0，而EFGNAS*训练阶段与测试阶段分类准确率的τ值为-0.066 7.以上数据说明EFGNAS在训练阶段和验证阶段、训练阶段和测试阶段均具有较高的相关性，同时也证明了EFGNAS模型的鲁棒性较强.

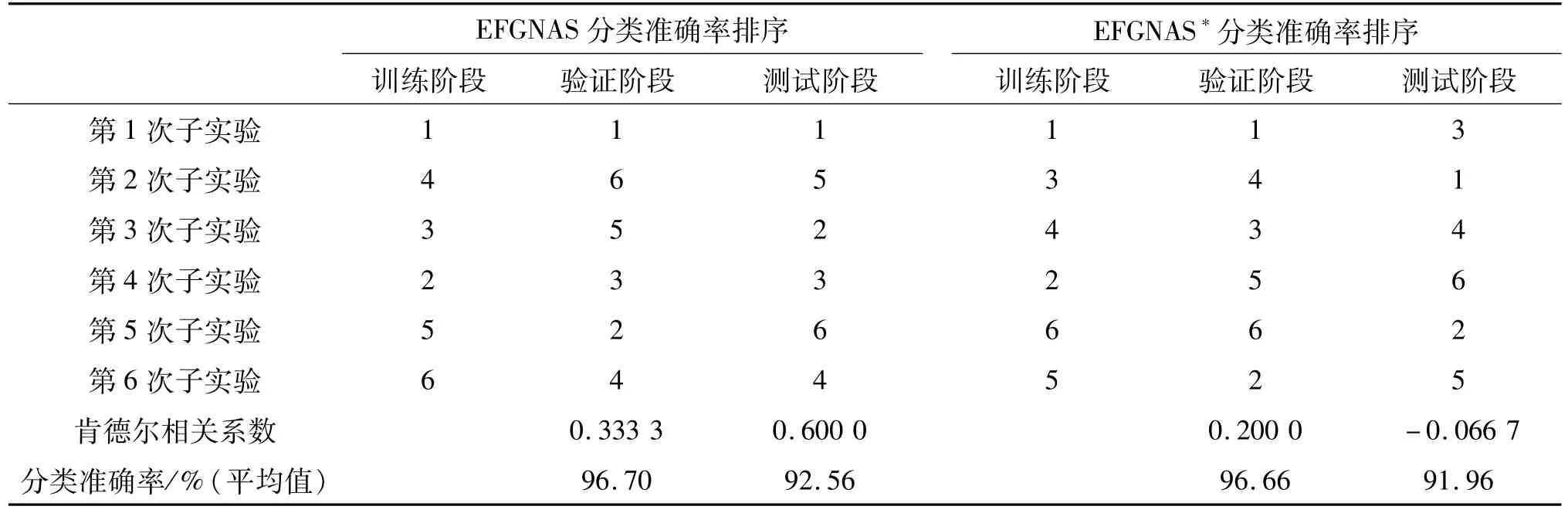
表5 EFGNAS和EFGNAS*分类准确率肯德尔相关性系数Tab.5 Comparison of search-evaluation Kendall coefficients and classification accuracy by EFGNAS＆EFGNAS*

3 结论

针对目前大多数图神经网络注重研究对象实体特征信息、忽略与边相关的特征信息的问题，本文提出了基于边缘特征提取的架构搜索算法自动设计网络架构.首先，提出了边缘特征图神经网络架构搜索的方法，设计了基于边缘特征的搜索空间和搜索算法；其次，将边缘与实体视为等价体，利用双层优化方法对实体信息和边信息进行了更新，采用边缘卷积和通道洗牌操作，在有限的计算资源下，获得了最佳的模型分类精度，并在速度和精度之间取得良好的平衡；最后，通过三维点云分类的实验，对所提出的方法进行了验证.仿真实验结果表明：本文所提出的方法能提升网络架构搜索算法的效率，防止网络过拟合，提高三维点云分类准确率，具有较强的鲁棒性.总的来说，目前图神经网络架构搜索取得了一定的效果，但在处理深层网络结构、大规模数据时，其适应性、可扩展性和效率方面仍有很大的改进空间.