Environmental and canopy conditions regulate the forest floor evapotranspiration of larch plantations

Zebin Liu,Ynhui Wng,＊,Pengto Yu,Lihong Xu,Songping Yu,b

a Key Laboratory of Forest Ecology and Environment of National Forestry and Grassland Administration,Ecology and Nature Conservation Institute,Chinese Academy of Forestry,Beijing,100091,China

b School of Soil and Water Conservation,Beijing Forestry University,Beijing,100083,China

Keywords:Larch plantation Forest floor evapotranspiration Reference evapotranspiration Soil water content Canopy structure

A B S T R A C T

1.Introduction

The long-term and massive forestation in dryland regions,such as the Loess Plateau in Northwest China,has contributed to mitigating some environmental problems(e.g.,soil erosion and desertification);however,it has created new problems including water yield reduction,soil drying up,and drought stress(Farley et al.,2005;Fu et al.,2011;Wang et al.,2011).In fact,the current forest/vegetation cover in the Loess Plateau has approached the limit of water resources and endangered the regional water supply security(Feng et al.,2016).In addition,such water use conflict is likely to be further exacerbated by climate change(El Shaer,2015)and further forestation.It is necessary to promote integrated and coordinated forest-water management based on the understanding and quantification of forest impacts on hydrological processes and water resources(Hu et al.,2018),especially in dryland regions with inherent water shortages.Evapotranspiration(ET),which is composed of canopy interception(Ic),tree transpiration(T),and forest floor evapotranspiration(FE),is usually the main water loss in forest ecosystems(Walker et al.,2019).Clarifying how ET components are affected by environmental and forest canopy conditions is critical to implement integrated forest-water management in changing environments.Compared with the plenty of studies on the variation inIcandT,fewer studies on the variation of FE have been reported,which limits the precise estimation and management of water use in forest stands.

The FE,which includes transpiration from understorey vegetation and evaporation from forest floor(i.e.,from the humus layer and mineral soil),has usually been assumed to have a small contribution to ET due to the low wind speed and available energy on forest floor compared to the canopy surface(Daikoku et al.,2008).In fact,the absolute value of FE and its contribution to ET varied widely among stands,such as the reported range of 8%–65% in boreal forests(Iida et al.,2009)and up to 50%in arid forests(Jiao et al.,2018;Schw¨arzel et al.,2019).This implies that the high contribution of FE to the ET of forests is indispensable.Therefore,it is very important to deeply understand and accurately predict the FE response to environmental and canopy conditions.

Weather conditions,such as vapour pressure deficit(VPD)and radiation,are the main driving forces of FE variation(Daikoku et al.,2008;Schw¨arzel et al.,2019).The complex impacts of many weather parameters can be simplified by the effect of just one comprehensive parameter of reference evapotranspiration(ETo).Han et al.(2019)reported that FE had a higher correlation with ETothan VPD or radiation.The canopy structure also affects FE by altering the forest floor environment(e.g.,mediating the amount and partitioning of available energy and the dryness/wetness degrees).FE generally decreases with the increasing leaf area index(LAI)of the canopy(Wang et al.,2016)and can even be ignored when the LAI is higher than 5(Kondo,2000).The surface soil moisture is another vital factor controlling FE.FE has been shown to be higher in wet soil zones than in dry soil zones(Di et al.,2019).On the whole,the impacts of environmental and canopy conditions on FE can be simplified as the FE response functions to ETo,VSM,and canopy LAI.Most existing studies have focused on the variation of these three influencing factors or on assessing the impacts of one or two of these factors(Raz-Yaseef et al.,2010;Han et al.,2019),while few studies have explored the comprehensive impact of all three main factors on FE.Additionally,climate warming and forest structure changes induced by deforestation,thinning,natural disasters(e.g.,snow damage),and growth are bound to alter the ET process and FE proportion in overall ET.Liu et al.(2021)predicted that climate warming(i.e.,an increase in ETo)will greatly impact forest ET under optimal soil moisture.However,few studies have attempted to separate the impact of EToor LAI on FE under varying environmental conditions(e.g.,soil moisture).As a result,the extent of the impacts of climate warming and forest structure changes on FE are not currently clear.

Empirical models are important tools for quantifying the impacts of environmental and canopy conditions on forest ET and FE components(Song et al.,2020;Liu et al.,2021).However,this kind of model generally needs to be able to reflect the coupled impacts of the main factors and must have a relatively simple structure(Liu et al.,2021).Although many excellent FE models coupling the impacts of multiple factors have been developed(Liu et al.,2018;Di et al.,2019;Han et al.,2019),simple-structured models considering the impacts of both environmental(i.e.,EToand VSM)and canopy conditions(i.e.,LAI)are rare.Following the evaporation coefficient proposed by Allen et al.(1998),the FE coefficient(Ke)in this study was defined as the ratio of FE to ETo(Ke=FE/ETo).Because of the observed positive relations between the FE coefficient and LAI and VSM(Yan et al.,2014,2017;Di et al.,2019),it may be feasible to couple theKe-LAI relation andKe-VSM relation to develop a simple but powerful FE model for predicting FE under changing environmental and canopy conditions.

Larix principis-rupprechtiiis a main tree species for afforestation in North and Northwest China.Such larch plantations play a very important role in producing timber and ecological services(e.g.,soil protection,hydrological regulation,and water supply).Changes in climate and stand structure due to tree growth and interference from nature(e.g.,snow damage)and management(e.g.,thinning)(Hao et al.,2012;Zhao et al.,2014;Xu et al.,2020)can strongly affect the ET of forest stands in this area.As reported in earlier studies,the FE of larch plantations can account for 27%–41% of the total ET in the Liupan Mountains region of Northwest China(Liu,2018).Thus,it is necessary to deeply understand and accurately quantify the FE responses to environmental and canopy conditions.In this study,we measured the FE of larch plantation during the growing seasons in 2019 and 2021,with simultaneous monitoring of meteorological conditions,canopy structures,and soil moisture.The objectives of this study were to(1)quantify the effects of VSM and LAI on the FE coefficient;(2)develop a simple FE model coupling the impacts of ETo,LAI,and VSM on FE;and(3)evaluate the impacts of ETo,LAI,and VSM on FE under different conditions.

2.Data and statistical analyses

2.1.Study site

The field experiment was conducted in the small watershed of Xiangshuihe(106°12′–106°16′E,35°27′–35°33′N)located in the Liupan Mountains,Ningxia,Northwest China(Fig.1),with an area of 43.7 km2and elevation range of 2,010–2,942 m.This watershed is characterized by a temperate semi-humid climate,with a mean annual air temperature of 5.8°C and mean annual precipitation of 618 mm.The main soil type is haplic greyxems.The forest cover in this watershed amounted to 82%with a contribution of 29%by plantations of which 90%is composed of

Larix principis-rupprechtii.

A pure larch plantation plot(30 m×30 m)was established(106°13′30′′E,35°30′50′′N),with a slope gradient of 37.6°and elevation of 2,290 m.This stand had an age of 38-years,a tree density of 932 stem⋅ha-1,a canopy density of 0.74,a mean tree height(H)of 15.79 m and a mean diameter at breast height(DBH)of 17.22 cm.The understorey vegetation was dominated by grasses with the dominant species of

Pteridium aquilinumandCarex hancokiana.The herb coverage and biomass were 0.4 and 0.54 t⋅ha-1,respectively.The humus layer biomass amounted to 20.4 t⋅ha-1.The soil bulk density,water holding capacity,and total porosity in the 0–30(0–60)cm soil layer were 1.00(1.07)cm3⋅cm-3,34.2%(33.2%),and 63.1%(60.5%),respectively(2020).

Continuous measurements were conducted in the growing seasons of 2019(June–September)and 2021(May–September);while the measurement in 2020 was affected by COVID-19,continuous data only covered a shorter period in the growing season,and thus were not used in this study.

2.2.Meteorological monitoring and ETo calculation

The meteorological data of precipitation(P,mm),air temperature(Ta,°C),solar radiation intensity(Rs,w⋅m-2),relative humidity(RH,%),and wind speed(μ,m⋅s-1)were monitored at a 5-min interval using an automatic weather station(Weatherhawk 232;Weatherhawk,Logan,UT,USA)in a meteorological observation field approximately 100 m away from the study plot.

Fig.1.Locations of the sample plot and study site.

Reference evapotranspiration(ETo)is defined as the evapotranspiration rate from a reference surface(i.e.,a hypothetical grass reference crop with specific characteristics)with unlimited soil water availability.As a comprehensive hydrometeorological parameter,EToexpresses the evaporative demand of the atmosphere under specific meteorological conditions and is independent of crop characteristics and soil factors(Allen et al.,1998).The ETo(mm)was calculated based on the observed meteorological data with the following formula(Allen et al.,1998):

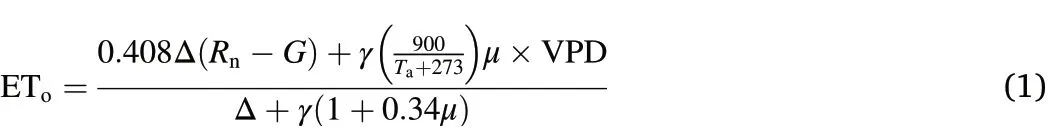
whereΔ(kPa⋅°C-1)is the slope of the saturation vapour pressuretemperature relationship;Rn(MJ⋅m-2⋅d-1)is the net radiation,which is calculated by Eqs.2–5;G(MJ⋅m-2⋅d-1)is the soil heat flux density,which is normally negligible at the daily scale(i.e.,assumed to be zero;Allen et al.,1998);VPD(kPa)is the vapour pressure deficit,which is calculated using air temperature and relative humidity(Campbell and Norman,1998);and γ(kPa⋅°C-1)is the psychometric constant.

whereRns,Rnl,Rs,Rso,Ra(MJ⋅m-2⋅d-1)are the net shortwave radiation,net longwave radiation,measured solar radiation,clear-sky radiation,and extraterrestrial radiation,respectively,Rais determined by the latitude of the station and the time of the year(Allen et al.,1998);σ is the Stefan-Boltzmann consent(σ=4.903×10-9MJ⋅K-4⋅m-2⋅d-1);TmaxandTmin(K)are the maximum and minimum temperatures;ea(kPa)is the actual vapour pressure,which is calculated using air temperature and relative humidity(Campbell and Norman,1998);andZ(m)is the station elevation.

2.3.LAI measurements

The canopy LAI was measured using an LAI-2200c canopy analyser(LI-COR,Lincoln,NE,USA)at 15 fixed points within the sample plot with a frequency of 2–3 times per month.For each LAI measurement,the mean LAI value of the 15 fixed points was observed.Each LAI measurement was repeated three times,and their mean was taken as the plot LAI.The LAI on each day within the measurement period was interpolated using fitted relationships between the measured LAI and the number of days in the year(DOY):LAI=2.97×10-6DOY3+1.56×10-3DOY2–2.52×10-1DOY+15.93(R2=0.97,P<0.01)in 2019 and LAI=4.22×10-8DOY3–2.61×10-4DOY2+1.08×10-1DOY–7.10(R2=0.98,P<0.01)in 2021.

2.4.Forest floor evapotranspiration and soil moisture measurements

The FE(i.e.,microlysimeter(ML)-measured evapotranspiration,FEML)was observed using microlysimeters(Fig.2),which consisted of an outer cylinder(20.5 cm in diameter and 40 cm in height),an inner cylinder(20 cm in diameter and 30 cm in height)with holes at the bottom for possible leaching,and a water basin(19.5 cm in diameter and 10 cm in height)to be placed under the inner cylinder.Three points at which the measured LAI was close to the plot mean LAI were selected for microlysimeter installation.The undisturbed soil monoliths with humus layer and possibly vegetation(i.e.,grasses)were first dug out and then fitted into the microlysimeters in May 2019.To minimize the impact of the possible slight soil disturbance during microlysimeter installation on the observed results,the data in May 2019 were not used in this study.At each measurement,the microlysimeter weight and seepage water volume were recorded using an electronic balance at a precision of 0.1 g and a volumetric cylinder,respectively,at approximately 18:00 every day(except rainy days).The daily FEMLvalue(in mm)was then calculated as the difference between the microlysimeter weights obtained in 2 consecutive days and the seepage water weight.In light of the difficulty of obtaining accurate FEMLvalues on rainfall days,the rainy-day FEMLdata were excluded in this study.The stand FEMLvalue was calculated as the mean of the three FEMLmeasurements.The daily FE coefficient(Ke)was calculated as the ratio of FE to the reference evapotranspiration using the formula ofKe=FEML/ETo.

Fig.2.The installation of microlysimeters at the forest floor and the structure of microlysimeters.

To obtain the dynamic VSM in the microlysimeters and on the forest floor,EC-5 soil moisture sensors(Decagon,Pullman,WA,USA)were installed at a 15-cm soil depth at each microlysimeter and the surrounding areas,and data were collected every 5 min using EM50 data loggers(Decagon,USA).

In most cases,the FE measured by microlysimeters did not represent the real FE because the VSM in the microlysimeter is different from the VSM on the forest floor(Benyon and Doody,2015).In this study,the real FE(mm,Liu et al.,2018)was calculated by inputting the VSM measured on the forest floor into the FE(FEML)model to replace the VSM measured in microlysimeters.In this study,the impacts of ETo,LAI,and VSM on the real FE were coupled using the model developed based on the microlysimeter data(see the FE(FEML)model section),and the differences between FE and FEMLwere compared to determine the impact of the difference in VSM between the microlysimeter and forest floor.

2.5.Forest floor evapotranspiration model

2.5.1.Model structure

The multiplicative function(i.e.,the Jarvis-Stewart(J-S)equation)is widely used to reflect the comprehensive effects of multiple factors on canopy conductance,transpiration,and evapotranspiration(Granier et al.,2000;Whitley et al.,2008;Liu et al.,2021).Since the FE coefficient is controlled by the LAI and VSM(Yan et al.,2014,2017),we assume that the impacts of LAI and VSM can be expressed as a multiplicative function,that is,Ke=f(LAI)×f(VSM);therefore,the basic framework of the FE(FEML)model can be expressed as:

wheref(LAI)andf(VSM)are the response functions ofKeto LAI and VSM,respectively.

The concrete response functions ofKeto LAI and VSM were determined using the upper-boundary-line(UBL)method(Schmidt et al.,2000);this method can capture the impact of a single factor while preventing/minimizing the interferences of other factors.First,scatterplots were created betweenKeand the LAI(VSM)data.Second,all the data were equally divided into five groups according to the actual measured variation range of LAI(VSM),and the data points higher than the meanKevalue plus one standard deviation were selected from each data group.Third,the data points that met the above-mentioned conditions were used to fit the UBL to reflect the response function of FE to each factor.

2.5.2.Model calibration and validation

The parameters in the FE(FEML)model(Eq.6)were fitted using the data collected on odd days and validated using the data collected on even days in 2019 and 2021.The model performance was evaluated using a combination of the coefficient of determination(R2)and the Nash-Sutcliffe efficiency coefficient(NSE).The NSE was calculated as follows:

whereyiandyi'are the measured and predicted daily FEML,respectively;yiis the mean of the observed FEML;andnis the number of samples.The model is considered to be satisfactory when the NSE value is higher than 0.6 and theR2value is close to 1(Dawson and Wilby,2001;Wilby,2005).

3.Results

3.1.Variation in environmental conditions and canopy LAI

The precipitation conditions differed obviously between the two study years(Fig.3a and b).In the wet year of 2019,the total precipitation(June–September)was 721 mm(54 rainy days),with 94 mm in June,219 mm in July,254 mm in August,and 154 mm in September;in contrast,in the dry year of 2021,the total precipitation(May–September)was 506 mm(55 rainy days),with 69 mm in May,52 mm in June,66 mm in July,97 mm in August,and 222 mm in September.The daily ETovalues varied greatly throughout the study period,with means of 2.05 and 2.44 mm⋅d-1and variation ranges of 0.2–3.9 and 0.18–4.45 mm⋅d-1in 2019 and 2021,respectively.

The VSM in the microlysimeter was obviously higher than that on the forest floor in cases of continuous heavy rainfall periods(e.g.,DOY 232–262 in 2019)and slightly lower than that on the forest floor in cases of drought periods(e.g.,DOY 200–230 in 2021)(Fig.3c and d).The mean(and variation range)of daily VSM in microlysimeters was 0.268(0.182–0.364)cm3⋅cm-3in 2019 and 0.214(0.127–0.419)cm3⋅cm-3in 2021.The corresponding values on the forest floor were 0.244(0.207–0.296)cm3⋅cm-3in 2019 and 0.201(0.139–0.248)cm3⋅cm-3in 2021.

The LAI showed similar variation patterns in both study years(Fig.3e and f),i.e.,increased during the early growing season(May and June),peaked in late July or early August,and thereafter declined gradually.The maximum LAIs of 4.12 and 3.74 occurred on DOY 216 in 2019 and DOY 201 in 2021,respectively.

3.2.Variation in the FEML and FE coefficient measured by microlysimeter

The FEMLon the days without any rainfall showed different variations in the two study years(Fig.4a and b).In 2019(June–September),the daily FEMLranged from 0 to 2.23 mm⋅d-1,with a mean of 0.93 mm⋅d-1.The monthly means of daily FEMLranged from 0.67 to 1.15 mm⋅d-1,with the lowest value in September and the highest value in July,respectively.In 2021(May–September),the daily FEMLranged from 0 to 2.34 mm⋅d-1,with a mean of 1.00 mm⋅d-1.The monthly means of daily FEMLvaried more obviously in the range of 0.44–1.66 mm⋅d-1,with the lowest value in August and the highest value in May.

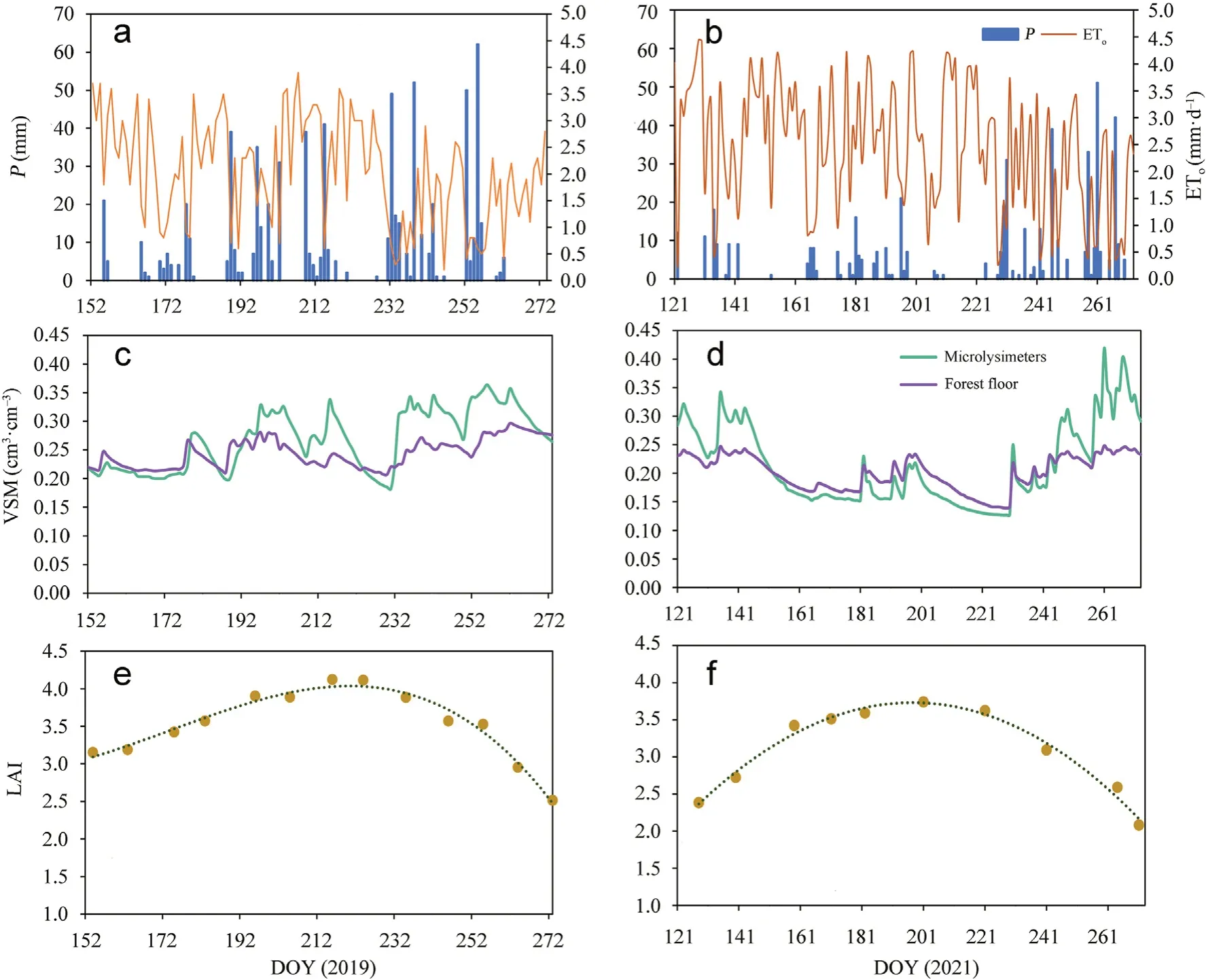
Fig.3.Variations in environmental conditions and canopy LAI in 2019(Jun.–Sep.)and 2021(May–Sep.).

Fig.4.Variation in the daily FEML and FE coefficient(Ke)on non-rainfall days in 2019(Jun.–Sep.)and 2021(May–Sep.).Two unconnected points indicate that there was rainfall during this period.

The FE coefficient showed a somewhat similar variation trend during the study periods of both years(Fig.4c and d).The FE coefficient first decreased gradually at the beginning of May or June,reached a minimum in July or August,and thereafter increased gradually.However,due to the more severe drought,the FE coefficient decreased substantially in July and August of 2021 compared with 2019.The mean daily FE coefficient was 0.36 in 2019 and 0.33 in 2021.

3.3.The FE(FEML)model

According to the UBL,the response of the FE coefficient to VSM conformed to a logarithmic growth function(Ke=f(VSM)=a1×ln(VSM)+b1),that is,the FE coefficient increased first rapidly and then slowly with rising VSM(Fig.5a);the response of the FE coefficient to LAI conformed to a power function attenuation(Ke=f(LAI)=a2×LAIb2),that is,the FE coefficient decreased slowly with rising LAI(Fig.5b).

Based on the FE coefficient equation(FEML=Ke×ETo)and the multiplication equation(Ke=f(LAI)×f(VSM)),the aforementioned single-factor response relationships were coupled to form a FE(FEML)model:FE(FEML)=[a1×ln(VSM)+b1]×(a2×LAIb2)×ETo.The parameters(Table 1)of this model were further fitted using the FEML,ETo,VSM,and LAI data measured on odd days and then validated using the data measured on even days in 2019 and 2021.The comparison between the simulated and measured values(Fig.6a and b)showed that the FE(FEML)model had a high accuracy(R2=0.81 and NSE=0.80 in calibration;R2=0.81 and NSE=0.78 in validation).

3.4.Comparison of FEML and FE

The VSM data from microlysimeters and forest floor were input into the newly developed FE(FEML)model to determine the impact of VSM difference between the microlysimeter and forest floor on FE estimation.In the growing season of 2019 and 2021,the estimated mean daily FEMLwas 0.95 and 0.98 mm⋅d-1,respectively(Table 2),which was higher than the corresponding mean daily FEs of 0.90 and 0.95 mm⋅d-1calculated by inputting the measured VSM on the forest floor into the FE(FEML)model.If the measured FEMLdata were used as the FE,the real FE would be overestimated by 5.56% and 3.16% in 2019 and 2021 due to the difference in VSM between the microlysimeter and forest floor,respectively.

Furthermore,the ratios between FE and FEMLvaried monthly(Table 2).In the months with high rainfall(e.g.,July,August,and September in 2019 and May and September in 2021)and thus high VSM(>0.22),the monthly means of daily FEMLwere higher than the calculated monthly means of daily FE,exhibiting an overestimation of 5.88%–18.28%.However,in the months with low rainfall(e.g.,June in 2019 and June,July,and August in 2021)and thus low VSM(≤0.22),the monthly means of daily FEMLwere lower than the calculated monthly means of daily FE,displaying an underestimation of 2.06%–17.65%.

Table 1Fitted parameter values and the accuracies of FEML model.

Table 2Comparison between the FEML and FE estimated using FE(FEML)model.

From an overall perspective,the real daily FE was underestimated when the VSM in microlysimeters was below 0.215(62.9% of the field capacity)and was overestimated when the VSM in microlysimeters was above this value(Fig.7).

3.5.Variation in FE with ETo,LAI,and VSM

Under various LAI and VSM conditions,the FE increased linearly with rising ETo(Fig.8).The smaller the LAI and the larger the VSM were,the higher the variation rate of daily FE was as the ETorose.For example,given an LAI of 2.5 and a VSM of 0.1(0.4),the daily FE increased by 0.08(0.65)mm⋅d-1per 1-mm⋅d-1increase in ETo.Given an LAI of 4 and a VSM of 0.1(0.4),the daily FE increased by 0.06(0.50)mm⋅d-1per 1-mm⋅d-1increase in ETo.

Under various EToand VSM levels,FE decreased in the form of a power function with rising LAI.The larger the EToand VSM were,the higher the variation rate of daily FE was as the LAI rose(Fig.8).For example,given an EToof 1 mm⋅d-1and a VSM of 0.1(0.4),the daily FE decreased by 0.01(0.10)mm⋅d-1per unit LAI increase.Given an EToof 4 mm⋅d-1and a VSM of 0.1(0.4),the daily FE decreased by 0.05(0.40)mm⋅d-1per unit LAI increase(Fig.8a and d).

Under various EToand LAI levels,FE increased logarithmically with rising VSM.The larger the EToand the smaller the LAI were,the higher the variation rate of daily FE was as the VSM rose(Fig.9).For example,given an LAI of 2.5 and an EToof 1(4)mm⋅d-1,the daily FE increased by 0.19(0.76)mm⋅d-1per increase in VSM of 0.1.Given an LAI of 4 and an EToof 1(4)mm⋅d-1,the daily FE increased by 0.15(0.58)mm⋅d-1per increase in VSM of 0.1(Fig.9a and d).

4.Discussion

4.1.Effects of VSM and LAI on the FE coefficient

The soil moisture determines the amount of soil water available for FE;thus,under given EToconditions,the FE and FE coefficient increases as VSM rises.Typically,the FE(or FE coefficient)increases with rising VSM until reaching the field capacity,and thereafter becomes less sensitive(Or et al.,2013).For example,Yan et al.(2014)reported that the FE coefficient increased linearly with rising VSM in the range of 0.12–0.26.However,a different variation pattern of FE coefficient with VSM was observed in this study,i.e.,the FE coefficient first increased rapidly and nearly linearly with rising VSM until 0.18 and then slowly as VSM further increased(see Fig.5a).This might be related to the differences in soil structure and texture(Or et al.,2013)because the experiment of Yan et al.(2014)was conducted in cultivated farmland soil with different soil structures(e.g.,soil water holding capacity and porosity)from the natural forest soil in our study.

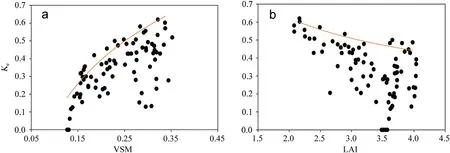
Fig.5.Response of daily Ke to VSM and LAI on odd days in 2019(Jun.–Sep.)and 2021(May–Sep.).

Fig.6.Comparison between the observed and simulated daily FEML in the cases of calibration(on odd days in 2019 and 2021,left)and validation(on even days in 2019 and 2021,right).

Fig.7.Variation in the difference between the calculated daily FEML and FE when the VSM data in the microlysimeter(ML)and at the forest floor were input into the FEML model.Negative or positive values indicate that the real FE is under-or overestimated.

The canopy structure also affects the FE and FE coefficient,mainly by moderating the amount of energy reaching the forest floor.For example,it was previously reported that the FE coefficient varied among seasons due to canopy development(Zhao et al.,2013).LAI is the total leaf area per unit ground area and is a core parameter used to characterize canopy structures(Liu et al.,2015).Several studies have reported that the FE coefficient decreased slowly with rising LAI with a nonlinear relationship(Daikoku et al.,2008;Yan et al.,2017;Di et al.,2019).A similar result was found in this study,in which the FE coefficient responded to the LAI with a power function attenuation trend(Fig.5b).As the LAI increased,the amount of energy available for FE decreased gradually due to the increase in canopy shading(Liu et al.,2018);thus,both the FE and FE coefficient decreased.

Obviously,the seasonal variation in the FE coefficient in both 2019 and 2021 was related to soil moisture and canopy LAI.Within the 2 study years,the FE coefficient was low in the middle growing season and high in the early and late growing seasons.Similar results have been reported in studies conducted on deciduous forests(Wilson et al.,2000;Daikoku et al.,2008).This variation pattern was mainly attributed to the seasonal variation in canopy LAI of forests.However,the FE coefficient was obviously lower in the middle growing season(July and August)of 2021 than in 2019,mainly due to the lower VSM in the middle growing season of 2021 compared with that in 2019(Fig.3c and d).Additionally,much weaker seasonal variation in the FE coefficient was observed in 2019 than in 2021,mainly due to the lower variation coefficient of VSM(LAI)of 0.19(0.12)in 2019 compared with that of 0.33(0.16)in 2021.

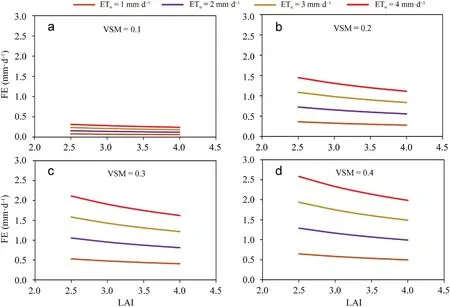
Fig.8.Variations in simulated daily FE with LAI under various ETo and VSM levels.

Fig.9.Variations in simulated daily FE with VSM under various ETo and LAI levels.

4.2.FE model coupling the effects of multiple factors

Under natural conditions,FE is influenced by a variety of factors,among which the main factors are meteorological conditions(e.g.,ETo),canopy structure(e.g.,LAI),and soil characteristics(e.g.,VSM)(Raz-Yaseef et al.,2010).In this study,a simple daily FE model was established to couple the effects of ETo,VSM,and LAI by multiplying the response functions of the FE coefficient to individual factors.This new model has a higher precision(R2=0.81)but fewer parameters(i.e.,four parameters)than other existing models(Liu et al.,2018;Di et al.,2019;Han et al.,2019)and thus has large application advantages in FE estimation.

Apparently,few studies have separated and quantified the impacts of individual driving factors on FE.Although several studies have shown that the individual driving factors have various effects on FE under changing environmental conditions(Yan et al.,2014;Wang et al.,2016),these differences have not been quantified previously.In our study,we quantified the effects of individual factors on FE under various environmental conditions with the help of the FE model developed herein(Figs.8 and 9).These quantitative results can provide references for integrated forest-water management under changing environmental conditions.For example,previous studies(e.g.,Wang et al.,2021)showed that the impacts of increased canopy water consumption caused by climate warming on local water resources can be mitigated by appropriate thinning(i.e.,reducing LAI).However,this study showed that under constant soil water conditions(e.g.,VSM=0.4),the decrease in canopy LAI(from 4 to 2.5)can obviously enhance the impact of climate warming(e.g.,an EToincrease)on FE,i.e.,an elevated increase rate of daily FE from 0.50 to 0.65 mm⋅d-1per 1-mm⋅d-1increase in ETo.This finding indicated that forest thinning can lead to a complex impact of climate warming on forest evapotranspiration,i.e.,reduced canopy transpiration and canopy interception vs.the offsetting effect of enhanced FE.Therefore,to achieve the predetermined goals of saving water resources,it is necessary to conduct specific water management measures(e.g.,maintaining proper canopy shading to control the undergrowth and soil surface temperature)after thinning to trade off the water consumed in the canopy layer and on the forest floor.In addition,the FE proportion is relatively high in areas where deforestation or clear-cut events or snow/storm disasters have occurred,and quantitative evaluations of the impacts on FE from the change in forest stand structures(e.g.,the canopy LAI)cannot be ignored(Daikoku et al.,2008).In our study,we quantified the impact of canopy LAI on FE and found that under constant meteorological conditions,the higher the soil moisture was,the greater the impact of LAI change on FE was.This finding indicated that the same degree of thinning can lead to higher FE increases in wetter areas with higher soil moisture than in dryer areas.

4.3.Implications for daily FE estimations

Several methods can be used to estimate daily FE,such as model simulation(Ritchie,1972;Aydin et al.,2005),stable isotope measurement(Yepez et al.,2003),microlysimeter measurement(Benyon and Doody,2015;Zhao et al.,2015;Di et al.,2019),eddy-covariance method(Iida et al.,2009),and chamber measurement(Raz-Yaseef et al.,2010).Among these options,microlysimeter measurement is the most commonly used for estimating FE,but several studies have reported that the microlysimeter method can overestimate the real FE in rain-rich periods due to the higher VSM in microlysimeters than that in forest-floor as a result of the exclusion of water extraction by tree roots from microlysimeter soil(Daamen et al.,1993;Zhao et al.,2013;Wei et al.,2015).In this study,the VSM in microlysimeters was quite different from that on the forest floor,but the VSM in microlysimeters was not always higher than that on the forest floor.The phenomenon of higher VSM in microlysimeters appeared mainly in the periods after continuous or heavy rainfall.In addition to the exclusion of water uptake by tree roots,another possible reason could be the low water conductivity of the less porous bottom of the inner cylinder compared with the conductivity of natural soils on the forest floor.During heavy or continuous rainfall events,more water can be accumulated in microlysimeters,resulting in elevated VSM and FEML.Moreover,lower soil moisture in microlysimeters compared with forest floor was observed in this study under persistent drought conditions(e.g.,no or little rain fell for a long time).Under natural conditions,the soil water can move upwards from the deep and wet soil layers with higher water potential to the shallow and dry soils with lower water potential through soil capillary action or hydraulic lift of plant roots(Richards and Caldwell,1987).The exclusion of such upwards soil water movements in microlysimeters will result in lower VSM compared with that on forest floor.Additionally,the higher soil temperature in microlysimeters due to the relatively sealed microlysimeter environment compared to the forest floor environment(Evett et al.,1995)might lead to higher soil water loss through evaporation and transpiration(Fetzer et al.,2017).Therefore,some errors will arise when estimating FE directly using the microlysimeter measurements.

In this study,the FEMLand real FE were estimated by inputting the VSM data in microlysimeters and on the forest floor into the newly developed FE model,respectively.If the FEMLis simply viewed as the real FE in the semi-humid study area,the FE was more overestimated in the wet year with more rainfall(2019)than in the dry year with less rainfall(2021).Moreover,the FE was overestimated in months with more rainfall but underestimated in months with less rainfall.This indicates that the accuracy of FE estimation when directly using the microlysimeter measurement was obviously affected by the VSM and the amount of rainfall.Additionally,the real FE was underestimated when the VSM in the microlysimeter was below 62.9% of the field capacity at the daily scale.Generally,soil moisture lower than approximately 60% of field capacity indicates that the soil suffers drought(Hsiao,1973).Under dry soil conditions,water exchanges,such as the upward flow of soil water into the microlysimeter,was eliminated(Klocke et al.,1990),resulting in higher forest-floor VSMs than the measured values of the microlysimeter.The study area is characterized by a semi-humid climate,and seasonal drought often occurs.This leads to a more often underestimation of the real FE when directly using the microlysimeter measurement,which is different from the more often reported overestimation of FE values in humid regions(Benyon and Doody,2015).Therefore,it is necessary to exercise cautiously in comparing the differences in microlysimeter-measured FE values among various climate/rainfall/soil moisture conditions.

4.4.Limitations of this study and suggestions for future study

In this study,we only explored the impacts of the main factors(i.e.,ETo,LAI,and VSM)on forest floor evapotranspiration.Although the combined effects of the above factors can explain 81%of the variation in FE,the impacts of other factors cannot be ignored.For example,several studies have showed that the water content of the humus layer also has an obvious impact on FE(Baldocchi et al.,2000;Wilson et al.,2000).In the drying process of the humus layer(especially after rainfall),the water stored in the humus layer contributed greatly to FE.Additionally,the important impacts of both the quantity and quality of the humus layer on FE have been confirmed in some studies(Lafleur,1992).Therefore,much more attention should be given to the effects of other factors on FE in the future.

Previous studies have shown that soil temperature is also an important factor affecting FE(Fetzer et al.,2017;Di et al.,2019),and the difference in soil temperature between a microlysimeter and forest floor(Evett et al.,1995)will surely affect the estimation accuracy of real FE when using the microlysimeter measurement.Attentions must be given to the accurate understanding of the influences of factors leading to the soil temperature difference between the microlysimeter and forest floor for further improvement of the real FE estimation in the future.

5.Conclusion

In the studied plantation ofLarix principis-rupprechtiilocated in the Liupan Mountains of Northwest China with a semi-humid climate,the ratio of daily forest floor evapotranspiration(FE)to reference evapotranspiration(ETo)declined with rising canopy leaf area index(LAI)and decreasing volumetric soil moisture(VSM).A simple daily FE model coupling the effects of just three dominant factors(ETo,LAI,VSM)could explain 81%of the variation in daily FE.

All three factors showed varying effects on FE under changing conditions.The smaller the canopy LAI and the larger the VSM were,the higher the daily FE variation rate became as the ETorose;the larger the EToand VSM were,the higher the daily FE variation rate became as the canopy LAI rose;and the larger the EToand the smaller the canopy LAI were,the higher the daily FE variation rate became as the VSM rose.

Errors arose when estimating the real FE on the forest floor if directly using the microlysimeter measurement;whether the real FE was underor overestimated was mainly dependent on the soil moisture conditions related to the rainfall.

Future studies should further explore the responses of FE to soil temperature and humus characteristics(i.e.,the quantity,composition,and water content of the humus layer)and the impact of the soil temperature difference between the microlysimeter and forest floor on the real FE estimation.

Funding

This work was funded by the National Natural Science Foundation of China(41971038,32171559,U20A2085,and U21A2005)and the Fundamental Research Funds of the Chinese Academy of Forestry(CAFYBB2020QB004 and CAFYBB2021ZW002).

Authors'contributions

Zebin Liu:Conceptualization,Investigation,Methodology,Visualization,Writing-original draft.Yanhui Wang:Conceptualization,Validation,Supervision,Writing-Review & editing.Pengtao Yu:Writing-Review & editing.Lihong Xu:Writing-Review & editing.Songping Yu:Investigation.All authors read and approved the final manuscript.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.