基于连杆变换矩阵的空间机械臂运动误差分析及辨识

刘 茜,孙 军,刘传凯,谢 圆,张 宽,成子青

(1.中国科学院自动化研究所,北京 100190; 2.北京航天飞行控制中心,北京 100094;3.航天飞行动力学技术重点实验室,北京 100094)

1 引言

空间机械臂承担着舱外设备巡检、安装与更换,辅助航天员出舱和航天器回收与释放等在轨任务。目前,空间机械臂的任务规划和控制通过地面遥操作方式,同时通过遥测下传关节角数据,掌握空间机械臂在轨状态。准确的运动学模型是地面遥操作进行空间机械臂任务规划的基础。尽管在发射入轨前,空间机械臂已在地面完成标定和仿真验证,但由于太空重力释放和复杂在轨环境的影响,空间机械臂的运动学特性会发生改变,导致末端位姿精度降低,影响遥操作的准确性和安全性。有必要开展空间机械臂在轨辨识,获得能够精确反映空间机械臂在轨运行状态的运动学模型,提高末端位姿精度,支持在轨任务的顺利开展。

国内外研究人员针对机械臂运动学参数辨识开展了大量研究工作,主要归纳为基于DH模型和基于指数积公式的运动学参数辨识方法[1]。早期的运动学参数辨识大多采用基于DH 模型的方法,但传统DH 模型在处理相邻平行关节时会出现奇异性问题。Hayati[2]提出了一种改进DH 模型,在相邻平行关节处引入绕y轴转动的参数β,有效解决了上述奇异性问题。以改进DH 模型为基础,Zhuang 等[3-4]提了基于关节轴线单位向量表示的CPC 模型和基于关节姿态角度表示的MCPC 模型。Ma等[5]进一步对机械臂运动学误差来源进行了分析和建模,推导了误差传递方程。不同于一次性辨识全部运动学参数的方法,Jiang 等[6]提出了多维度辨识空间的概念,将不同量级的误差参数进行分组,分别辨识各组误差参数,以提高辨识精度。另一方面,基于指数积的运动学模型利用旋量描述运动,避免了DH 模型的奇异性问题。根据参考坐标系的不同,指数积的运动参数辨识方法又可分为基于全局指数积的辨识[7-8]和基于关节本体指数积的辨识[9-10]。尽管基于DH 模型和基于指数积公式的辨识方法得到的误差模型各不相同,但其核心思想都是通过末端位姿误差求解关节误差。

为保证误差模型求解过程的稳定性,广泛采用的方法是排除耦合运动误差参数,仅针对可辨识的运动误差参数进行辨识。Everett等[11]证明了R个转动关节和P个平动关节的机械臂具有(4R+2P+6)个可辨识的运动误差参数。但耦合参数对末端位姿误差的影响是不可忽略的,有必要分析运动误差参数,尤其是具有耦合特性的误差参数,评估其对末端位姿误差的影响。

从遥操作实践的角度考虑,现有的研究方法并未提供辨识构型优选的理论依据,没有解决辨识构型如何设计以及需要设计多少个辨识构型的具体问题。不同辨识构型下的末端位姿误差再现运动学误差的能力不同[12],有必要分析并建立辨识构型的优化目标,以提高空间机械臂运动误差参数的辨识精度。

针对空间机械臂由于太空重力释放和复杂在轨环境影响导致的运动学参数与地面重力环境不一致的问题,本文提出一种基于连杆变换矩阵的运动误差参数辨识方法。通过运动误差传递方程的建立及对运动误差参数的分析,研究关节误差参数耦合关系以及关节误差对末端位姿误差映射关系;设计基于辨识矩阵及避障空间约束等条件下的最优辨识构型选取原则,实现对运动误差参数的准确辨识及空间机械臂在轨运动的准确建模,从而有效提高地面遥操作对空间机械臂末端位姿的精确仿真和高精度控制。

2 空间机械臂运动误差传递方程

2.1 运动学模型

本文研究的空间机械臂是具有N自由度(N≥6)的串联机械臂。根据改进DH 参数[13]构建空间机械臂连杆坐标系,连杆两端相邻坐标系的变换矩阵如式(1)所示:

式中,i表示第i个连杆,i =1,2,…,N;αi-1表示沿xi-1轴,从zi-1轴旋转到zi轴的角度;ai-1表示沿xi-1轴,从zi-1轴移动到zi轴的距离;di表示沿zi轴,从xi-1轴移动到xi轴的距离;θi表示沿zi轴,从xi-1轴旋转到xi轴的角度。

空间机械臂末端工具坐标系相对于基坐标系的变换矩阵0TTool可以通过将连杆坐标系的变换矩阵依次相乘得到,如式(2)所示:

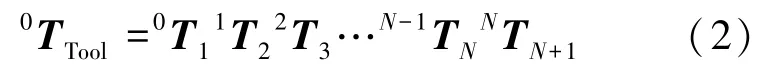
式中,NTN+1表示工具坐标系相对空间机械臂末端坐标系的变换矩阵。

2.2 运动误差传递方程

已知连杆坐标系变换矩阵的理论值为(i =1,2,…,N +1),则真实值i-1Ti可表示为理论值与误差值di-1Ti之和,如式(3)所示:

其中,i-1Δ 表示误差矩阵[14],见式(4):

式中,i-1δ和i-1m分别表示姿态误差矢量和位置误差矢量,i-1δ=[i-1δx,i-1δy,i-1δz]T,i-1m=[i-1mx,i-1my,i-1mz]T;S(δ)表示矢量δ的反对称矩阵,见式(5):

空间机械臂末端工具坐标系变换矩阵的真实值0TTool可表示为式(6):

忽略高阶误差项,公式(6)可推导出式(7):

其中,平移矢量P表示为P=[px,py,pz]T;旋转矩阵R表示为式(9):

进一步将公式(7)写为多元线性方程组的形式,得到从关节位姿误差到末端位姿误差的运动误差传递方程,如式(10)所示:

式中,0ΓTool和Γ分别表示末端位姿误差向量和关节位姿误差向量,0ΓTool= [0mTool,0δTool]T,Γ=[0Γ,1Γ,…,N-1Γ,NΓ]T;i-1Γ表示第i个关节的误差向量,i-1Γ=[i-1m,i-1δ]T(i=1,2,…,N+1);JΓ表示关节位姿误差雅可比矩阵,JΓ=[0JΓ,1JΓ,…,N-1JΓ,NJΓ] ;i-1JΓ表示第i个关节的位姿误差雅可比矩阵,如式(11)所示:

3 空间机械臂运动误差分析及辨识构型优选

3.1 关节误差参数可辨识性分析

关节误差参数之间的相互独立性决定了各个误差参数的可辨识性,而参数独立性取决于误差传递方程中关节位姿误差雅可比矩阵中列向量的相关性。本文将通过推导关节位姿误差雅可比矩阵的列向量相关性,对关节位姿误差参数的可辨识性展开分析。

式中,i-1fk(i =1,2,3,…,N;k =1,2,…,6)表示关节位姿误差雅可比矩阵的6 个列向量,如式(13)所示:

在DH 参数中,和均为常数,空间机械臂第i +1 关节的位姿误差雅可比矩阵第三列向量iJΓ3与第i关节的位姿误差雅可比矩阵第二列向量i-1JΓ2和第三列向量i-1JΓ3存在线性相关关系;第i +1 关节的位姿误差雅可比矩阵第六列向量iJΓ6与第i关节的位姿误差雅可比矩阵第二列向量i-1JΓ2、第三列向量i-1JΓ3、第五列向量i-1JΓ5和第六列向量i-1JΓ6存在线性相关关系。

空间机械臂第一关节的位姿误差向量具有4 个独立误差参数和2 个耦合误差参数,最后一个关节的位姿误差向量具有4 个独立误差参数。除第一关节和最后一个关节外,空间机械臂的任一关节位姿误差向量具有2 个独立误差参数和2 个耦合误差参数,且耦合误差参数与上一关节的误差参数存在线性相关关系。从关节位姿误差雅可比矩阵列向量相关性的角度得到了与Everett 等[11]推导的(4R+2P+6)个可辨识元素相同的结论。

消除位姿误差雅可比矩阵的线性相关列向量,公式(10)可改写为式(14):

式中,J*Γ表示改写后的关节位姿误差雅可比矩阵,有J*Γ= [0JΓ,1J*Γ,…,N-1J*Γ,NJ*Γ] ,且各关节的位姿误差雅可比矩阵i-1J*Γ=[i-1JΓ1,i-1JΓ2,i-1JΓ4,i-1JΓ5](i =2,3,…,N +1);Γ*∈R(6+4N)×1表示改写后的关节位姿误差向量,是由6N个位姿误差参数构成的具有(6+4N)行元素的列向量,有Γ*= [0Γ*,1Γ*,…,N-1Γ*,NΓ*]T;i-1Γ*表示第i个关节改写后的误差向量,见式(15):

根据最小二乘法原理,得到式(16):

式中,K表示用于辨识的测量数据量。通过相同辨识构型重复测量的方式[15]考虑随机误差的影响,则对于N自由度空间机械臂,仅需要设计(6N)/N=6 组辨识构型对误差参数进行辨识,即K =6k,k表示相同辨识构型下的重复测量次数;J*Γi和0ΓTooli分别表示第i次测量得到的关节位姿误差雅可比矩阵和末端位姿误差向量,i =1,2,…,K;J表示关节位姿误差参数的辨识矩阵,J=[(J*Γ1)T(J*Γ2)T…(J*ΓK)T]T。通过测量多组的关节构型和末端位姿误差,可实现对空间机械臂关节位姿误差参数的辨识。

3.2 辨识构型优选

最小二乘法辨识结果的精度取决于辨识矩阵J的选取,而辨识矩阵由辨识构型计算得到。因此,辨识构型的优选有利于提高最小二乘法的辨识精度,从而提高误差参数辨识结果的准确性。辨识构型优选问题可以描述为如式(17)所示的优化问题:

辨识构型优选问题不需要考虑测量随机误差的影响,因此取重复测量次数k =1,则K =6;FK(·)表示空间机械臂从关节空间到笛卡尔空间的正运动学方程;θ表示空间机械臂关节角构型,θ= [θ1,θ2,…,θN]T;xtool表示末端在基坐标系下表示的位姿;χmea表示具备末端位姿测量条件的位姿集合;θimin和θimax分别表示第i关节的最小值和最大值;χrobot表示空间机械臂外包络空间;χobs表示障碍空间。

上述优化问题可通过基于改进粒子群优化算法求解[16],求解流程如图1 所示。

图1 改进粒子群优化算法求解流程图Fig.1 The flow chart of improved particle swarm optimization algorithms

改进粒子群优化算法中对粒子适应度Wi的定义为式(18):

式中,i为在总体为N的粒子群中的第i个粒子。

算法中的速度Vi和粒子Yi的更新分别由式(19)和(20)实现,即:

式中,u为迭代次数;c1和c2为加速度常数,一般取c1=c2=[1,2.5] ,本文中取c1=c2=1.5;pBesti和gBesti分别为粒子i的个体极值和整个粒子群的全局极值。

随后需要进行粒子间基因的交叉和变异操作。粒子Ykj与粒子Ylj之间进行交叉操作以及粒子Yij发生基因变异操作的定义分别由式(21)和(22)实现,即

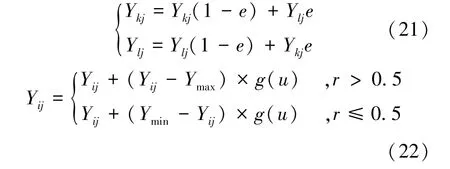
式中,e为[0,1] 间的随机数;Ymax和Ymin分别为粒子Yij的上界和下界;g(u)为迭代次数u和最大迭代次数umax的函数,即g(u)= r2(1-u/umax)2;r和r2为[0,1] 间的随机数。

4 仿真验证

为验证本文提出的运动误差辨识方法的有效性,搭建了七自由度空间机械臂仿真模型,坐标系关系如图2 所示。空间机械臂运动学参数的理论值如表1 所示[17]。

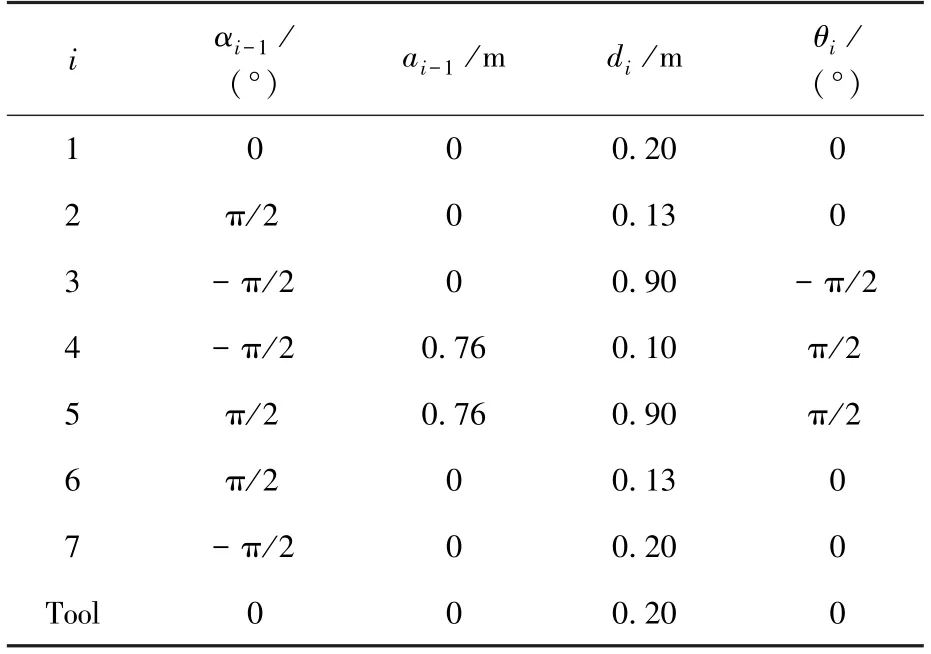
表1 空间机械臂运动学参数理论值Table 1 Theoretical values of kinematic parameters

图2 七自由度空间机械臂DH 坐标系Fig. 2 DH coordinates frames of the 7 - DOF space manipulator

空间机械臂各个关节的误差由姿态误差矢量和位置误差矢量组成,仿真预设的误差参数如表2 所示,误差参数的量级参考文献[18]。

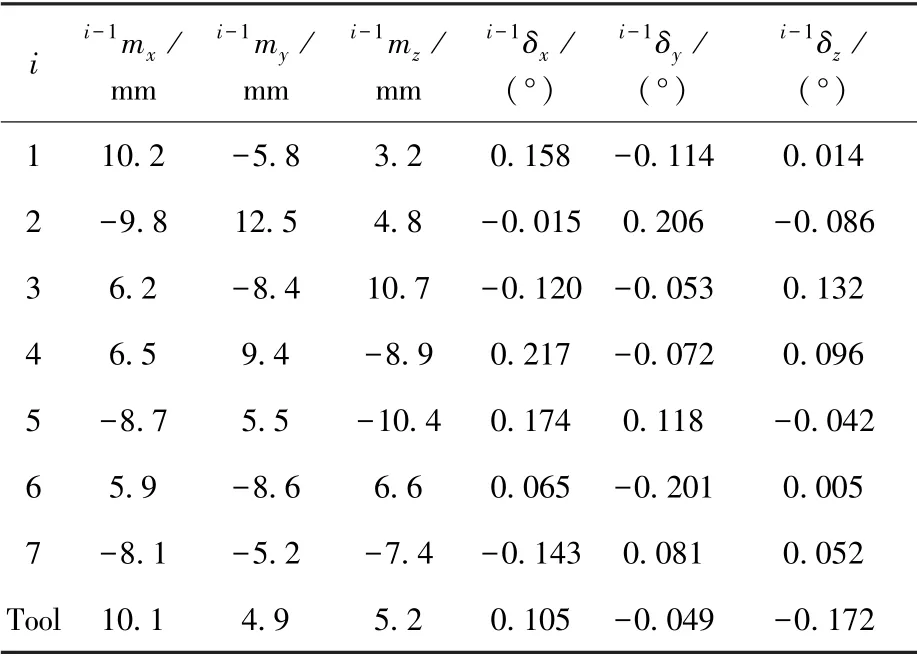
表2 空间机械臂仿真预设误差参数Table 2 Presupposed errors of space manipulator

一般辨识构型表示通过试凑法选的一组关节运动在[- 120°,120°] 范围内的辨识构型(表3)。本文采用的试凑原则为:首先根据关节角度运动范围随机选取关节构型;在此基础上验证空间机械臂是否与障碍空间发生碰撞,如果所选构型下空间机械臂发生碰撞,则需要重新进行关节构型的随机选取,直到所选构型满足碰撞规避。

表3 空间机械臂一般辨识构型Table 3 Identifiable configuration of space manipulator单位:(°)

同时,根据3.2 节提出的辨识构型优选原则,采用基于改进粒子群优化算法对上述空间机械臂进行求解,得到关节运动在[- 120°,120°] 范围内的最优辨识构型,如表4 所示。

表4 空间机械臂最优辨识构型Table 4 Optimized identifiable configuration of space manipulator单位:(°)

根据3.1 节的分析,上述七自由度空间机械臂的关节位姿误差向量Γ*具有(6 + 4 × 7)=34个元素。第一个关节位姿误差向量由6 个元素组成,表示为0Γ*= [0mx,0my,0mz +1mz,0δx,0δy,0δz +1δz]T,其中包含4 个独立误差参数和2 个耦合误差参数;末端位姿误差向量由4 个独立误差参数组成,表示为7Γ*= [7mx,7my,7δx,7δy]T;其他关节位姿误差各由2 个独立误差参数和2 个耦合误差参数组成,见式(23):

基于最小二乘法原理辨识得到上述20 个独立误差参数和14 个耦合误差参数的辨识结果,如表5 所示。其中,辨识值的误差γerror见式(24):

表5 误差参数辨识结果Table 5 Identification of error parameters

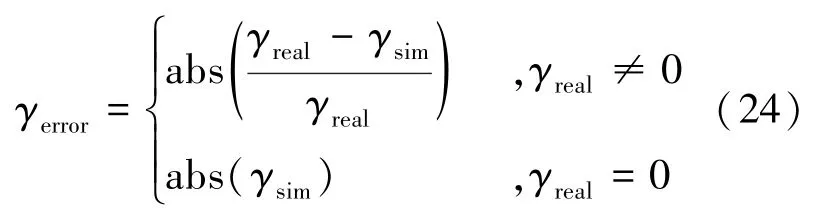
式中,γreal和γsim分别表示预设真实值和仿真辨识值。

如表5 中所示,一般辨识构型下得到的辨识结果精度较差,平均误差为11.95%,最大误差为70.83%;最优辨识构型下的辨识结果的精度显著提高,平均误差为1.11%,最大误差为6.67%。上述结果验证了本文提出的运动误差分析方法及辨识构型优选方法的有效性。

在仅有关节构型和末端位姿数据的情况下,耦合误差中的参数不能唯一确定。但由于耦合误差参数中各个参数的选取不影响机械臂末端位姿的精度,因此,基于以最优辨识构型得到辨识结果,本文给出一种可能的空间机械臂辨识误差参数,如表6 所示。

表6 空间机械臂辨识误差参数Table 6 Identification errors of space manipulator

采用梯形速度算法[19]规划空间机械臂从初始构型[10,-100,80,100,-80,90,5]运动到目标构型[60,30,20,20,30,75,15]的轨迹。运动误差补偿前后的末端位姿曲线如图3 所示。

图3 空间机械臂末端位姿及误差图Fig.3 Pose and pose error of space manipulator in conditions with or without compensation

运动误差补偿前,空间机械臂末端位姿精度较差,最大位置误差达到25 mm,最大姿态误差达到0.45°。采用本文提出的方法对空间机械臂进行运动误差参数辨识,提高了空间机械臂的末端位姿精度,最大位置误差减小到1 mm 以下,最大姿态误差减小到0.1°以下。综上,通过七自由度空间机械臂运动仿真,验证了基于连杆变换矩阵的空间机械臂运动误差辨识方法的有效性和准确性。

5 结论

1)基于运动误差传递方程,分析了关节运动误差到末端运动误差的传导机理,开展了运动误差参数的可辨识性分析,实现了耦合运动误差参数对末端位姿误差的线性表达。

2)提出了空间机械臂辨识构型优选原则,通过改进粒子群算法实现对空间机械臂最优辨识构型的求解。

3)通过七自由度空间机械臂的运动仿真实例,验证了本文所提出的基于连杆变换矩阵的运动误差参数辨识方法的有效性,该方法能够有效提高空间机械臂运动学模型的准确性。

4)本文仿真验证基于理想的末端位姿测量结果,并未考虑测量噪声的影响。另一方面,尽管耦合运动误差中各个参数并不直接影响空间机械臂末端位姿精度,但会影响动力学仿真的精度。因此,未来将进一步考虑测量噪声的影响,同时开展耦合运动误差的分析,以期得到更加准确的运动学模型。