金属隔膜翻转过程中的锥段抗失稳能力评价研究

范 凯乔艳伟施 华

(1.上海空间推进研究所,上海 201112; 2.上海空间发动机工程技术研究中心,上海 201112)

1 引言

作为推进系统中的主要压力容器,推进剂贮箱是影响航天器安全服役的核心组件之一[1]。在众多推进剂贮箱类型中,金属隔膜式贮箱因具有轻质、长寿命、高可靠性、防晃动、推进剂剩余量可测等特点,被广泛使用在经常变轨、姿态调整频繁、机动性强的飞行器中,以实现推进剂贮存和管理功能。典型的金属隔膜式贮箱结构及工作过程示意如图1 所示。作为金属隔膜式贮箱的核心部件,金属隔膜位于贮箱壳体腔内,并在赤道位置与壳体密封连接。其上表面与贮箱壳体内壁构成初始容积占比约2%～3%的气腔,用于贮存增压气体;下表面与壳体内壁构成容积占比约97% ～98%的液腔,用于贮存液体推进剂。当贮箱工作时,通过贮箱气口向气腔内持续充入规定压力的气体,金属隔膜在气液两腔的压差作用下,从赤道位置处开启由气腔向液腔方向的规则翻转,进而将液腔内的液体推进剂从液口持续排出,直至隔膜下表面完全与贮箱内壁贴合。基于上述过程可实现向飞行器发动机供给不夹气的纯液推进剂。因此,金属隔膜的翻转可靠性对金属隔膜贮箱的工作至关重要。

图1 金属隔膜贮箱结构及工作示意图Fig.1 Structure and working process of metal diaphragm tank

近些年,有关隔膜翻转行为的影响因素研究众多。强洪夫等[2]研究发现隔膜锥角对隔膜翻转行为的影响程度与隔膜材料有关,同时隔膜的承载能力随锥角的增加而减小。袁森等[3-4]首先针对隔膜预弯边半径对隔膜翻转行为的影响开展研究,结果发现隔膜预弯边半径越大,隔膜翻转应力越小,但翻转过程中越容易出现偏心现象;随后采用正交试验设计的分析方法对预弯边半径、隔膜厚度和隔膜锥角进行了组合分析,得到了3 个参数的影响程度差异。程桐等[5]和黄韬等[6]均指出为了保证隔膜的正常翻转,应采用适当的变壁厚设计。张绪虎等[7]系统研究了材料弹性模量、硬化指数和屈服强度对隔膜翻转性能的影响,发现屈服强度的影响程度明显高于其他2 个因素。

此外,国内外研究人员还针对金属隔膜的翻转行为开展了一系列理论分析、试验和数值模拟研究。朱智春等[8]基于变钜理论,在应力-应变本构关系中纳入流变韧性,对隔膜翻转过程中的变形进行了理论分析;Radtke[9]针对金属隔膜的结构设计、选材和制造工艺开展了试验研究;Harry等[10]针对用于绿色推进剂贮存和管理的直径254 mm 的钛制隔膜进行了翻转试验研究;张增亭[11]基于大变形弹塑性有限元法,采用MSC.MARC 软件对纯钛TA1-A 隔膜的翻转变形进行了模拟计算,并进行了试验验证;宋冠华等[12]基于ABAQUS 软件提出隔膜充压翻转的现实动态仿真法,针对不同充气速率下的隔膜翻转压差和偏心程度进行模拟研究。

上述研究表明,金属隔膜的翻转行为受到几何尺寸和材料性能的综合影响。不合理的隔膜几何尺寸或材料性能均会导致隔膜无法实现规则翻转。然而,隔膜不规则翻转形式众多,不仅包括上述研究中广泛涉及的翻转不充分、翻转偏心、隔膜顶部垮塌、隔膜褶皱,还包括工程中较为常见的隔膜锥段径向塑性失稳形式。由于该种形式发生在隔膜翻转早期,其引起的隔膜泄漏造成的影响程度更大。目前国内外尚无针对这一不规则翻转形式的理论分析及评定方法报道,仅有少数仿真研究报道。然而,基于有限元方法的非线性屈曲分析结果强烈依赖初始缺陷的选择,合理的初始缺陷需要通过大量实验测试统计得到,实验成本较大。因此,需要发展一种成本较低、工程应用方便的金属隔膜锥段抗塑性失稳能力评价方法。

本文以纯钛隔膜为研究对象,采用有限元数值模拟的方法,对具有不同锥段几何参数的隔膜锥段最大翻转压力prmax和等效锥壳塑性失稳压力ppb进行计算;并结合隔膜翻转试验结果分析prmax-ppb关联图用于隔膜翻转过程中的锥段抗塑性失稳能力评价和锥段径向失稳预测的可行性。

2 数值模拟和试验

2.1 隔膜材料和几何参数

选择纯钛隔膜为研究对象。纯钛的真应力-应变关系遵从Ramberg-Osgood 关系,如式(1)所示[13]。

其中,ε和σ分别为真应变和真应力,σ0为屈服强度,ε0(=σ0/E)为屈服应变,E为杨氏模量,α为Ramberg-Osgood 常数,n为硬化指数。试验测得纯钛在室温下的力学性能如表1 所示。真应力-应变曲线如图2 所示。

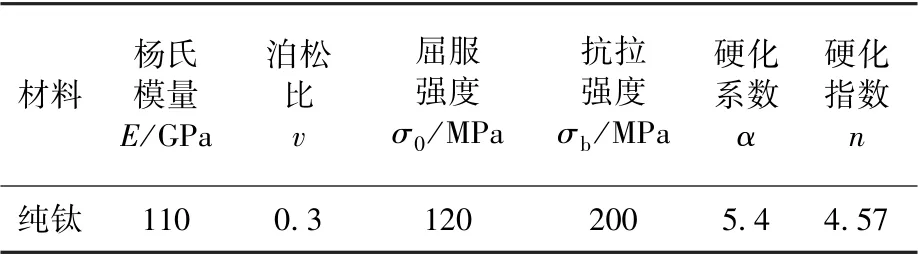
表1 室温下纯钛的力学性能Table 1 Mechanical property of purity titanium at room temperature

图2 室温下纯钛的真应力-应变曲线Fig.2 True stress-strain curve of purity titanium at room temperature

采用典型的金属隔膜进行数值模拟和试验,隔膜结构由球冠段、过渡球壳段、锥段和翻边段组成。其中锥段几何参数包括锥段型面参数(锥段长度L0、锥角β、锥底直径D)和锥段壁厚t,具体如图3 所示。

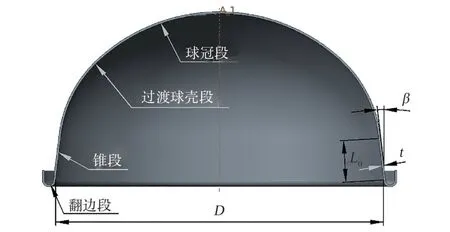
图3 典型的金属隔膜结构Fig.3 Structure of the typical metal diaphragm

本文选取3 组不同锥段型面参数的金属隔膜(D-1、D-2 和D-3),并针对每组隔膜选取5 组不同的锥段壁厚t,具体的隔膜锥段几何参数如表2所示。

表2 隔膜锥段几何尺寸参数Table 2 Geometric parameter of the diaphragm conical section

2.2 有限元模型

采用ABAQUS 软件分别对上述隔膜进行建模。由于隔膜结构对称,故建立1/4 结构模型,D-1-1 隔膜的有限元模型如图4 所示。实际金属隔膜贮箱中,隔膜在翻边段末端处与贮箱壳体通过焊接方式连接,故在此位置设置边界条件ENCASTRE(U1=U2=U3=UR1=UR2=UR3=0);在结构对称平面上分别设置边界条件XSYMM(U1=UR2=UR3=0)和ZSYMM(U3=UR1=UR2=0)。为确保仿真结果的有效性,开展了网格敏感性验证。结果表明,当隔膜锥段网格尺寸不大于2 mm×2 mm 时,隔膜锥段应力幅值和分布以及翻转压力曲线已无明显变化。考虑到计算效率和计算精度,隔膜锥段采用1 mm×1 mm 的网格尺寸,其他区域采用3 mm×1 mm 的网格尺寸。图4 中隔膜D-1-1 模型共包含12 561 个单元及12 480个节点,网格类型选择壳单位(S4R)。模拟过程中,在隔膜外表面施加均布载荷。

图4 隔膜有限元模型Fig.4 Finite element model of metal diaphragm

通过对2.1 节中各隔膜进行有限元模拟,可以计算得到隔膜锥段翻转过程中的压力曲线和应力分布。

2.3 锥壳塑性失稳压力

典型的锥壳几何尺寸如图5 所示,其中L为锥段长度,r1为锥顶半径,r2为锥底半径,t为锥段壁厚。

图5 典型的锥壳几何尺寸Fig.5 Geometry of the typical conical shell

通过将锥壳转换为等效圆柱壳,可以得到锥壳的弹性失稳压力[14],无量纲锥段长度如式(2)所示。

有效半径如式(3)所示。

无量纲失稳压力如式(4)所示。

锥壳弹性失稳压力如式(5)所示。

由于式(5)中的E仅为材料弹性范围内的模量,为了得到塑性失稳压力,可以将弹性模量E替换为考虑了材料进入塑性后模量的切线模量Et。

式(1)进行微分得到式(6):

由式(6)可得切向模量为式(7):

将式(7)中的Et代替式(2)中的E,得到锥壳弹塑性失稳压力为式(8):

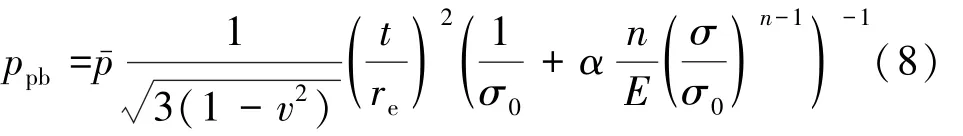
2.4 隔膜翻转试验

根据2.1 节中的隔膜材料和几何尺寸生产隔膜翻转试验件。隔膜翻转试验采用隔膜排放试验系统(图6)进行。将隔膜安装至工装上,隔膜与工装形成密闭容腔(相当于贮箱的气腔),并将该容腔与转注罐通过管路连接。试验过程中通过充气增压将转注罐中的试验介质(纯净水)挤入密闭容腔中,进而挤压隔膜开始翻转。通过上述试验可以准确观察隔膜翻转过程中的锥段径向失稳现象。

图6 隔膜排放试验系统Fig.6 Diaphragm air reversal test system

3 结果与讨论

3.1 隔膜锥段最大翻转压力prmax 的计算

图7 为 3 组锥段型面参数(D-1、D-2 和D-3)下,不同锥段壁厚t所对应的隔膜锥段翻转压力曲线(横坐标x为隔膜顶点的轴向位移)。从图中可以看出,不同锥段型面参数的隔膜锥段翻转压力pr变化趋势和幅值不同。针对相同锥段型面参数的隔膜,随着锥段壁厚t的增加,锥段翻转压力曲线逐渐升高。通过各压力曲线可得到各隔膜锥段最大翻转压力prmax。

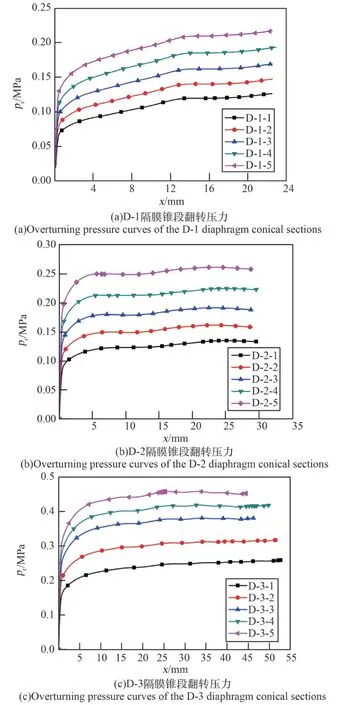
图7 三组锥段型面参数下不同锥段壁厚t 所对应的隔膜锥段翻转压力Fig.7 Overturning pressure curves of the diaphragm conical sections with different thicknesses t under three molding surface parameters

3.2 隔膜等效锥壳塑性失稳压力ppb 的计算

图8 为 D-1-1 隔膜在其锥段最大翻转压力prmax时的应力云图。从图中可以看出,靠近翻转处存在一定长度的未翻转锥段应力超过隔膜材料的屈服强度(120 MPa)。基式(7)可得该部分锥段的切线模量,见式(9):

图8 D-1-1 隔膜在最大翻转压力时的应力云图Fig.8 The stress contour at the maximum overturning pressure for the D-1-1 diaphragm

由于该模量远远低于材料弹性模量(E=110 000 MPa),进而导致该部分锥段为发生径向失稳的最薄弱位置。将该锥段定义为隔膜等效锥壳,其塑性失稳压力ppb可以用于表征隔膜的抗锥段径向失稳能力。

为了计算各隔膜等效锥壳塑性失稳压力ppb,首先通过隔膜在锥段最大翻转压力prmax时的应力云图,测量得到隔膜等效锥壳长度L、锥底半径R和锥顶半径r。再将上述参数带入式(2)～(8),计算得到各隔膜的等效锥壳塑性失稳压力ppb。

3.3 隔膜翻转试验结果

针对2.1 节中的各隔膜生产试验件,进行隔膜翻转试验。试验中观察了各隔膜在翻转过程中的锥段径向失稳情况,如表3 所示。图9 为典型的隔膜锥段径向失稳形貌(D-1-1 隔膜)和隔膜锥段未径向失稳形貌(D-1-3 隔膜)。

图9 隔膜锥段翻转形貌Fig.9 Overturning morphology of diaphragm conical section

表3 隔膜翻转过程中的锥段径向失稳情况统计Table 3 Summary of conical section radial buckling in the diaphragm overturning process

3.4 prmax 和ppb 的关联

根据3.1 和3.2 节得到的各隔膜的最大翻转压力prmax和等效锥壳塑性失稳压力ppb,可以得到两者的关联,如图10 所示。

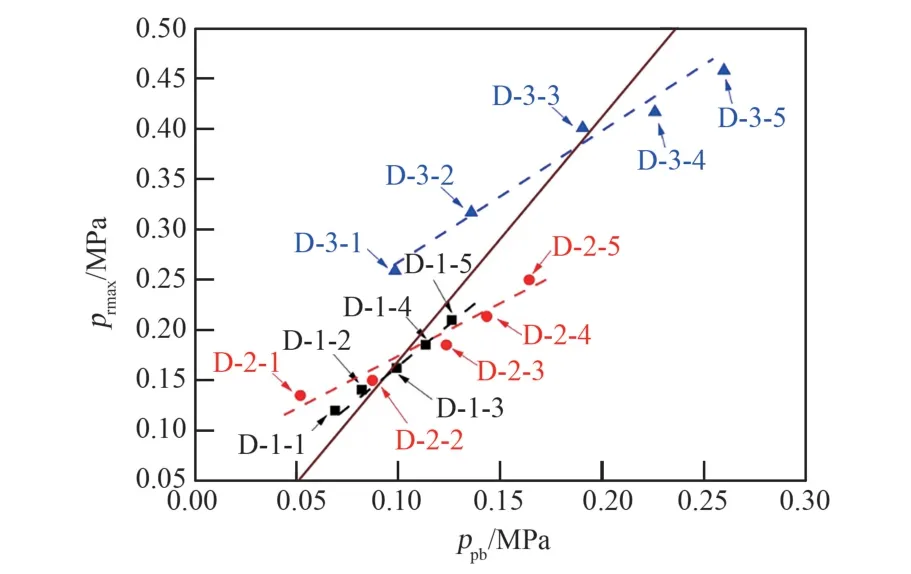
图10 不同锥段几何参数的纯钛隔膜锥段最大翻转压力pr max 和等效锥壳塑性失稳压力ppb 的关联Fig. 10 Correlation of the maximum overturning pressure prmax and equivalent conical shell plastic buckling pressure ppb for the purity titanium diaphragms with different conical section geometric parameters

从图中可以看出,3.3 节中在翻转过程中发生锥段径向失稳的隔膜数据点与未发生锥段径向失稳的隔膜数据点分别位于一条分割线DL的两侧。对该分割线DL进行线性拟合,拟合后的关系式如式(10)所示。

针对位于分割线DL左上方区域数据点对应的隔膜,锥段最大翻转压力prmax较高程度地超过等效锥壳塑性失稳压力ppb(k=(prmax+0. 085)/ppb,2.986＜k＜4.237),此时隔膜锥段的抗失稳能力较低,进而造成在翻转过程中发生径向失稳;针对位于分割线DL右下方区域数据点对应的隔膜,锥段最大翻转压力prmax低于或较低程度地高于等效锥壳塑性失稳压力ppb(2.040＜k＜2.336),此时隔膜锥段的抗失稳能力较高,进而在翻转过程中未发生径向失稳。针对分割线DL附近的数据点所对应的隔膜,锥段最大翻转压力prmax高于等效锥壳塑性失稳压力ppb的程度处于临界状态(2.383＜k＜2.746),此时通过略微增加隔膜锥段壁厚t,可使隔膜锥段抗失稳能力提升,进而在翻转过程中由发生径向失稳过渡为不发生径向失稳。此外,针对每组锥段型面参数确定的隔膜,不同锥段壁厚对应的数据点分别呈线性关系。分别对3 种锥段型面的隔膜(D-1、D-2 和D-3)数据点关联线RL进行了线性拟合,如式(11)～(13)所示。

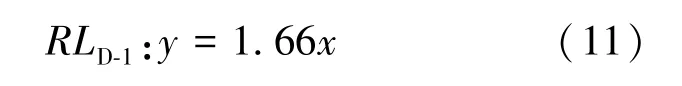
从图10 中可以看到,随着锥段壁厚t的增加,每组隔膜数据点分别沿对应关联线RL从分割线DL左上方区域逐渐靠近分割线DL,再越过分割线DL进入右下方区域并逐渐远离分割线。这表明,增加隔膜锥段壁厚t可以一定程度地提升隔膜翻转过程中锥段的抗径向失稳能力。此外,3 组隔膜的关联线RL斜率均大于1,随着关联线RL斜率从kD-2=1.05 增加至kD-3=1.44,再增加至kD-1=1.66,相同等效锥壳塑性失稳压力增幅Δppb所对应的锥段最大翻转压力增幅Δprmax逐渐增加。表明当隔膜材料确定时,隔膜锥段抗失稳能力受锥段几何参数(锥段长度L0、锥角β、锥底直径D和锥段壁厚t)的综合影响。从隔膜D-2至D-3 再至D-1,锥段壁厚t对锥段抗失稳能力的影响较其他因素减弱,进而通过增加确定比例壁厚的方式提升隔膜锥段抗径向失稳能力的效果逐渐减弱。因此,可通过关联线RL的斜率对采用壁厚增加方案提升隔膜锥段抗失稳能力的效果进行评价。

此外,prmax-ppb关联图中的分割线DL表示了纯钛隔膜翻转过程中发生锥段径向失稳的临界状态,即该分割线为纯钛隔膜锥段失稳的临界曲线。因此,基于prmax-ppb关联图,可通过数据点与分割线DL的相对位置关系进行隔膜翻转过程中的锥段抗失稳能力评价和锥段径向失稳预测。具体方法为:针对纯钛材料的隔膜,以等效锥壳塑性失稳压力ppb为横坐标,锥段最大翻转压力pxmax为纵坐标,构成隔膜prmax-ppb关联图。将分割线DL(式(10))作为评定曲线绘制在评定图中。评定曲线将评定图划分为2 个区域,曲线左上方区域为危险区,曲线右下方区域为安全区。针对某一待评定纯钛隔膜分别计算其锥段最大翻转压力prmax和对应的等效锥壳塑性失稳压力ppb,绘制评定点(ppb,prmax)于评定图中,对该隔膜锥段径向失稳进行评定。当评定点位于安全区时,表示该隔膜翻转过程中不会发生锥段径向失稳;当评定点位于危险区时,表示该隔膜翻转过程中会发生锥段径向失稳。同时,根据评定点到评定曲线的垂直距离可以评估该隔膜翻转过程中的锥段抗失稳能力,该距离越大,锥段的抗失稳能力越高。

基于上述方法的隔膜锥段抗失稳能力评价和锥段径向失稳预测过程简单、有效,并且成本较低,可推广至其他材料隔膜的结构优化设计中。

4 结论

1)当隔膜材料确定时,在不同锥段几何参数的隔膜prmax-ppb关联图中,发生锥段径向失稳的隔膜数据点与未发生锥段径向失稳的隔膜数据点分别位于一条分割线DL的两侧。

2)每组锥段型面参数确定的隔膜,不同锥段壁厚t对应的数据点分别呈线性关系;通过増加隔膜锥段壁厚t可以一定程度提升隔膜翻转过程中锥段的抗径向失稳能力。

3)基于prmax-ppb关联图,可通过数据点与分割线DL的相对位置关系进行隔膜翻转过程中的锥段抗失稳能力量化评价和锥段径向失稳预测;可通过关联线RL的斜率对采用壁厚增加方案提升隔膜锥段抗失稳能力的效果进行量化评价。