对高考中一道三角不等式的再探究

安恺凯，查晓东

(江苏省天一中学，江苏无锡，214101)

2020全国Ⅱ卷(理科)的导数题中引入了与三角函数相关的不等式，打破了若干年来超越函数ex、lnx与带参二、三次函数的综合题统治导数题位置的惯例，试题的设置角度和方式都较为新颖.文[1]从命题背景、解题方法、类似问题、备考感想四个角度对此题做了详细剖析，恰巧笔者在讲解此题时，学生提出了一个合乎情理又富有想象的猜想，笔者“顺藤摸瓜”得到两个更具一般性的推广，与文[1]探究角度颇有不同，现将探究该问题的心路历程整理如下，以飨读者.

1 真题再现

(2020年全国Ⅱ卷理科数学第21题)已知函数f(x)=sin2xsin 2x，

(1) 讨论f(x)在(0，π)上的单调性；

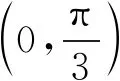
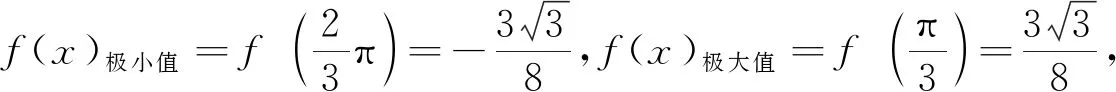
(法二)由均值不等式可得f2(x)=4sin6xcos2x=

2 问题推广

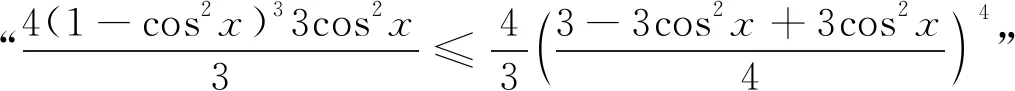
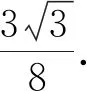
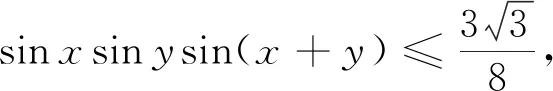
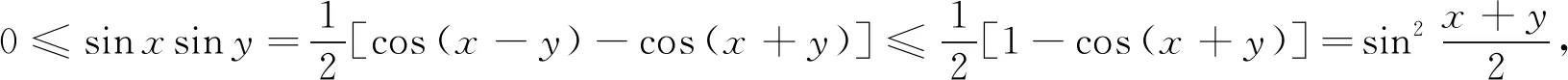
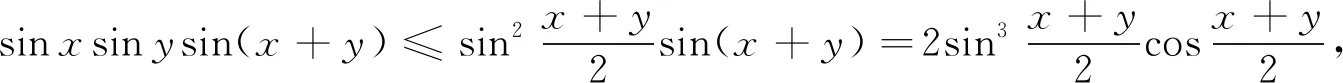
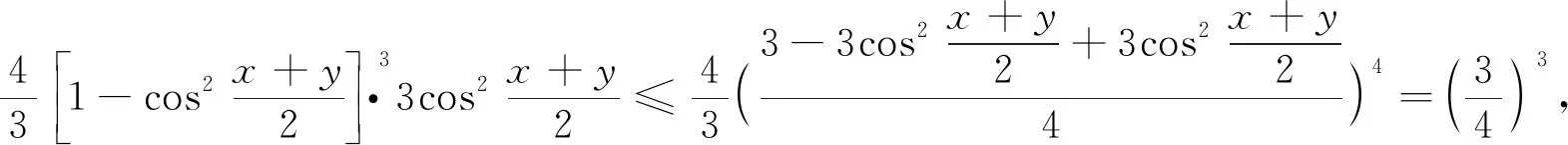
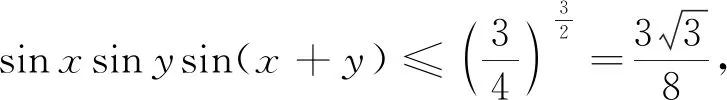
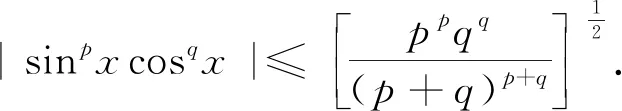
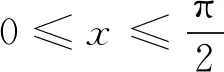
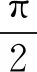
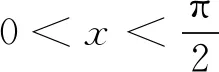
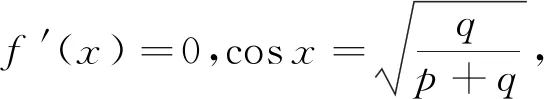
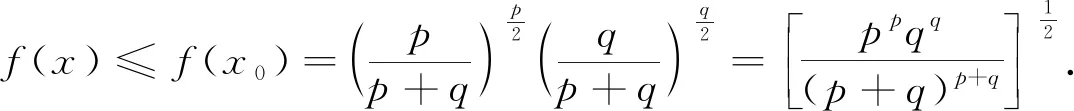
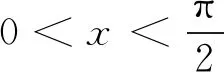
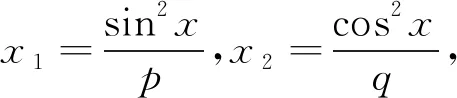
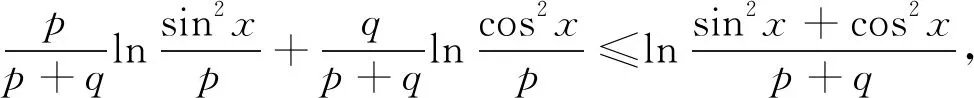
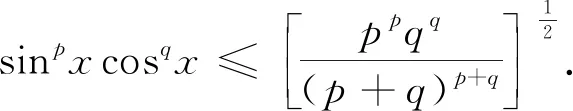
评析因此第(2)问中结论也是推广2中“p=3，q=1”的特殊情形，《课程标准》指出：“逻辑推理主要表现为：掌握推理基本形式和规则，发现命题和提出命题，探索和表示论证过程，理解命题体系，有逻辑地表达与交流.” 纵观整个命题推广，笔者经历了“学生提出问题——师生共同讨论——精细严格求证”，有效地培养了学生掌握逻辑推理基本形式的能力，学会有逻辑地思考问题的能力，以及把握事物发展脉络的能力.

3 结束语

问题是数学的心脏，对一道富有价值的问题“穷追不舍”的探究能激起学生的好奇心，并使学生的创造力发挥出来.在这道高考题的推广过程中，笔者与学生们一起经历“不断咀嚼—反复琢磨—再三玩味”的过程，经历那种紧张状态，并享受那种发现的喜悦.学生正处于一个易受外部影响的年龄段，这样的经历可能会悄然培养学生对问题致力/努力/深度思考的爱好，并且会让学生对数学的情感产生终身积极的影响，同时也有效地培养了学生的思维品质和理性精神，厚植了学生的逻辑推理等数学学科核心素养.