“三新”背景下高中数学课堂生成实践与思考

冯 阳

(苏州市相城区望亭中学，江苏苏州，215100)

教育家陶行知指出，教师的职责重在指导学生，通过激发学生的学习兴趣，最终让学生“自得”和“自动”，教师的教与学生的学，都是以“做”为中心的.这种通过教学来培养学生养成终身学习能力的观点恰恰与现在发展学生自主学习能力的核心素养相对应.这种目标不是一些应景的、空洞的口号，而是与学生数学课堂上的健康发展紧密联系的，需要教师、学生在教、学、做中进行有效沟通.新版教材中有大量体现时代要求和“潮流”的具体实例，既能激发学生的社会参与兴趣和探知欲望，培养其实践能力和创新意识，又发展了数学核心素养，形成理性思维.

本文主要从课堂教学出发，以新教材人教A版高中数学必修第一册4.3.1《对数的概念》为例，阐述笔者教、学、做合一课堂的教学设计思路与教学实践中的一些做法及思考，力求提高学生的学习品质和数学素养.

1 课前思考

本节内容是对数函数的基础，是高中数学知识体系中的重要一环.《普通高中数学课程标准》中明确指出：“很多数学概念是从实际生活中通过理想化的形式抽象出来的，学习概念的有效方式就是让学生经历数学化和寻找实际意义的互逆过程.”对数是为解决天文学中繁杂的运算而产生的，是人类突破固有，创造新知的重要表现.在课堂教学中，教师应当精心设计，把前人遇到的问题通过情景设置呈现给学生，让学生通过经历过程，形成概念生成的一般规律，激励学生勇于挑战，大胆创新，从而提升数学素养，进一步做到学、做合一.

对数概念教学，如果直接把概念灌输给学生，那教师的“教”只体现在把单一的知识传递给了学生，而没有发挥学生“学”的主体作用，这种没有经历“做”的学习过程，掌握的知识是毫无生命力的，学生的思维品质也不会得到提高.所以，课堂教学的目的是为能够促进学生有深度的“学”，教师的“教”的活动应当始终围绕这个目的展开.“教”的主要方式是引导学生自主探究，在“做”中发现问题、提出问题、解决问题.教师是“教”的主体，“教”的主旨是学生在自主探索时引导方向，让学生和问题直接对话；学生是“学”的主体，“学”应该在教师的引导下，积极地发现问题，在探究中提出问题、发现新知识，进而解决问题并构建新的认知结构.

本节课对数概念的学习，学生前面有过一些经验，比如分数、负数、无理数等，这些数的产生，都是运算“瓶颈”下的突破，学生对数的发展有了初步的思维和直观想象，但纵向联系能力仍显不足，教学中通过问题情境的创设，在“做”中再次让学生经历运算瓶颈，由此萌发渴望，寻求突破.

2 教学过程生成

2.1 创设情境，引出问题

问题1：已知经过x年后与某地景区人数是2001年的y倍，x、y满足关系式y=1.11x.如果要求经过多少年游客人次是2001年的2倍，3倍，4倍，……，该如何解决？

上述问题是教材上的一则引例，于学生而言可能挑战太大，会使其无从下手.可以考虑相对简洁的问题，比如可以引入棋盘麦粒问题.

问题2：棋盘上第一格放2粒麦粒，第二格放4粒，第三格放8粒，第四格放16粒，依次这样放，我们容易得到第x格与那一格的粒数y之间函数关系为y=2x，x∈N*，那么从第几格开始，放的麦粒数多于10，多于100，多于1000，多于10000？

问题3：若上面的“x∈N*”改为“x∈R”,是否存在实数x，使得2x=3？若存在，求出x，若不存在，请你说出理由.

问题2通过学生的自主求解，唤醒已掌握的指数幂运算和指数函数相关知识，激发学生的学习兴趣，又起到适应运算的过程.对于问题2中的几个问题，因为非常容易解答，可以让学生来展示运算成果，增强自信心；对于问题3学生根据指数函数的性质，可以确定x是唯一存在的，但指数方程的求解采用已有的知识无法求解，引发了学生的认知障碍，能够激发学生的探究欲望.

2.2 经历认知，建立重构

问题1：在求指数方程时，没有现成的运算工具.同学们学过哪些运算方法呢？

问题2：为什么要学习减法、除法、开方运算？

问题3：类比思考如何解决上面的问题？

引导学生积极探索，通过合作交流自己的发现，教师的“教”要做到点到为止，把“学”和“做”的主动权交给学生.通过学生的互动与思考，让学生经历数的运算发展，类比得到以下结论：

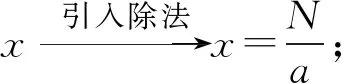
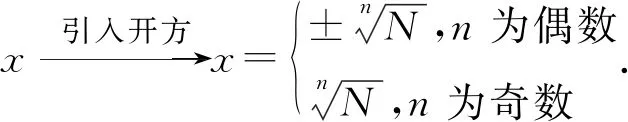
上述环节，教师的“教”主要负责巡视，倾听各组讨论情况，发现问题并提醒.类比以上过程，明确减法、除法、开方运算是加法、乘法、乘方运算发展的必然结果，并且都是可逆互化的.进而教师可以自然而然的引导学生自编求解指数方程的问题.如下：

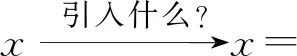
教师引导学生重新认知数的发展，激发学生创造新运算的渴望，体会引入对数的紧迫性和必要性.

2.3 突破思维，构建新知

(1) 对数的概念

在教学中，教师引入课后“阅读与思考”中的《对数的发明》纳皮尔发明的运算符号，即已知对数的底数和幂，求指数，需要引入新的运算符号，就是对数符号log.写出前面问题1、2、3的答案,引导学生归纳出对数的概念，教师讲解对数的概念x=logaN中，明确x，a，N的含义，log是英文单词logarithm(对数)前三个字母，它是一个新的符号.提醒学生注意对数读法和书写格式，a是底数，以下标形式出现，N是真数，它和log齐平.介绍常用对数和自然对数，这两个对数可以直接讲授，但提醒学生课后可以通过互联网等途径进一步了解无理数e、常用对数和自然对数，增强学习的自主学习能力和学习兴趣.

问题1：对数的底数a有什么限制？为什么？

教师引导，学生合作交流，并得到以下结论：

若a<0，则N区某些数值时，logaN不存在，例如：x=log(-3)2，所以a不能小于0；

若a=0，①则当N≠0时，logaN不存在，所以a=0不成立；②当N=0时，log00有了除了0以外的任意实数；

若a=1，① 则当N≠1时，log1N不存在；② 当N=1时，log11有无数个值；所以a=1不成立.

综上可知a>0,且a≠1.

通过教师提出的问题，引导学生自主地对a的范围进行分类思考，然后通过小组合作讨论交流完成，目的在于充分调动每个学生学习的积极性，提供展示学生想法的机会，并在合作学习中自我修正，上述过程充分体现了“做学合一”的理念.通过以上问题，加深学生对对数概念的理解，提升其逻辑推理能力和严谨思维品质.

问题2：通过对数概念的理解，指数式和对数式在表示x，a，N的关系时是否是同一个关系？

问题3：能够利用较为简洁的形式表达出指数、对数的这种关系吗？

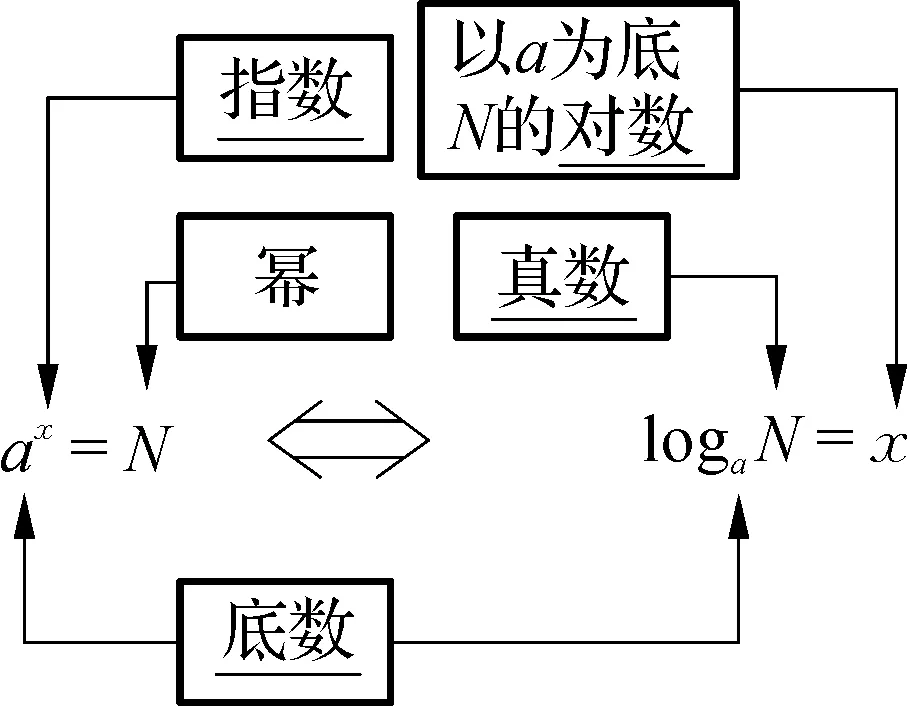
上述问题为了引导学生探究指数式与对数式的关系，通过前面问题的学习，探究发现，指数式和对数式是可以相互转化的，感知指数运算的可逆性.通过对x，a，N含义的深度理解，教师引导学生对两者的关系进行结构化和图象化表示,进而加深对对数的理解.如右图

(2) 通过例题掌握对数概念

问题1：(教材例1)把下列指数式化为对数式，对数式化为指数式：

① 54=625 ② ③

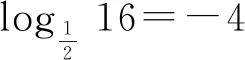
本例题让学生独立完成，教师可以挑选典型问题通过一体机等设备展示出来，从而让学生掌握指数式与对数式的相互转化规则，加深对数的概念理解.同时，教学中要求学生指出指数式与对数式互化时的注意点，培养学生严谨的思维品质.

问题2：请模仿上述例1，自己编写指对互化的问题，然后让同伴检测编写是否正确，并给予解答.

通过同伴之间相互出题，激发学生学习数学的热度，充分挖掘“做”的功能，加强指数式和对数式的互化运算能力.

问题3：观察例1中①、②、④、⑤对数式的结构，有什么发现？

引导学生归纳上述对数式都可化为logaab，引导学生求得logaab=b.通过解决上述问题，引导学生讨论出对数的两个重要结论：

① 复数和0没有对数；② loga1=0，logaa=1.

2.3 回顾反思，完善结构

3 教学反思

3.1 “教学做”中激发兴趣、探索生成

教学活动应当在学生固有的知识经验、知识能力之下设计.教师的“教”务必要有分寸感，引导、探讨、直接提问等方式都应围绕学生自主的“学”展开，目的就是让学生觉得“数学好玩”、数学的“做”很来劲，让学生成为积极的探索者、组织者、主导者.这样的课堂教学才能完成有深度的课堂生成.

3.2 “教学做”中巩固深化、提高能力

“教”的主体是教师，“学、做”的主体是学生，只有在课堂教学中让两者有机地结合，即让学生通过自主探究的模式自找问题、自找出路，才能更好的收获基本知识，感悟数学思想；通过学生“做”的活动，收获经验，感悟数学学习本质，发展数学核心素养，提升数学能力.