一个2+1维时间分数阶热传导模型的精确解及其演化现象

李 文，芮伟国

(重庆师范大学 数学科学学院，重庆 401331)

0 引 言

20世纪70年代以后，由于分数阶微积分理论具有较好的应用背景，曾在物理学、生物学、材料力学等领域得到了蓬勃的发展.基于分数阶微分方程在黏弹性力学，记忆性问题和反常扩散领域具有整数阶微分方程不可替代的优点，人们越来越重视分数阶微积分和分数阶微分方程的研究，致使分数阶微积分和分数阶微分方程在理论和应用方面都得到了飞速发展.如在热传导[1-4]、粘弹性材料[5-7]、生物学[8-10]、信号处理[11-13]以及磁力学[14-16]等领域有了较好的应用.然而，相比于整数阶微分方程的求解而言，分数阶微分方程的求解却显得十分的困难，由于整数阶微分方程领域的一些经典方法无法直接应用到分数阶微分方程的求解中去，因此,即便是一些简单的分数阶微分方程，也很难获得其精确的解析表达式，目前大多数关于分数阶微分方程的研究工作主要集中在解和正解的存在性讨论研究[17-18]以及解的稳定性和数值解等方面的研究.

1 分数阶热传导方程及其约化

与现有文献中的解的存在性研究工作和数值解研究工作所不同，本文将对下列2+1维的分数阶热传导方程进行精确求解研究：

(1)

该方程为Blasiak 在文献[3]中建立的非接触式端面密封传热过程的数学模型，刻画的物理问题是转子浸泡在润滑液中的热交换与热传导现象，其边界条件如下：

0≤r≤a,0≤z≤Lr

(2)

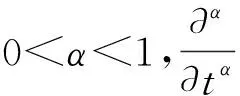
众所周知，物体在空气介质中与液态介质中的传热现象是完全不同的，在空气介质中的传热现象完全可以通过整数阶模型来加以描述和刻画，而在液态介质中(特别是具有反常扩散特性的介质中)，非常适合用分数阶模型来描述和刻画，这就是为什么文献[3]要把整数阶模型变成分数阶模型(1)的主要原因.

求解方程(1)的传统方法有两种：一种是积分变换法，另一种是变量分离法.积分变换法就是将方程(1)两边对时间变量t部分先施行Laplace变换，然后对空间变量(r,z)部分施行两种变量的Fourier变换，再通过它们的逆变换获得方程(1)的解.然而，由于方程(1)是变系数的方程，而且空间变量有两种，显然通过积分变换以及相应的逆变换来获得它的精确解的表达式是很困难的，最主要的原因还是逆变换往往无法实现.但如果利用传统的变量分离法求解方程(1)，那么就需要假设方程(1)的解形如：

u=W(z)R(r)T(t)

(3)

其中W(z)、R(r)、T(t)为3个待定函数.但由于方程中时间变量部分的分数阶微分算子与空间变量部分的整数阶微分算子的定义不同，运算法则也不一样，要把(3)代入(1)中实现3种变量的完全分离也不容易，因此，不妨把时间部分的待定函数固定成已知的特殊函数，比如Mittag-Leffler函数，这样(3)式就变成：

u=W(z)R(r)Eα(λtα)

(4)

其中λ为待定的非零常数.众所周知，分数阶微分方程的解中往往含有Mittag-Leffler函数或幂函数，因此这种做法是可行的.事实上，在Caputo型分数阶微分定义下，Mittag-Leffler函数有以下的良好性质：

(5)

利用性质(5),然后把(4)代入(1)得：

(6)

(7)

对(7)式进行变量分离得：

(8)

其中比值σ为任意常数.由于σ值的正负性直接影响着方程的解的性质，因此，在接下来的讨论中，将分两种情况对方程(8)的解展开讨论.

2 分数阶热传导方程的各种精确解及其蕴含的物理意义

情形1σ<0的情形

若σ<0不妨令σ=-ω2，此时方程(8)可化为下列两个二阶齐次线性常微分方程：

(9)

W″(z)+ω2W(z)=0

(10)

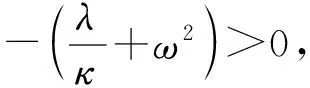
(11)

其中：p1、q1为任意常数，且v阶的第一类Bessel函数与0阶的第二类Bessel函数可表为：

对于方程(10)，此时ω为常数，此方程为二阶齐次线性常微分方程，故此方程的通解为：

W(z)=p2cosωz+q2sinωz(p2,q2为任意常数)

(12)

对于此问题，从模型所蕴含的物理意义来说，由于u=T-T0表示在坐标(r,z)上点与溶液的温差，其中T表示(r,z)点的温度，T0表示溶液介质的平均温度，视为转子于溶液介质表面与溶液介质的平均温度在初始时刻t=0时是相等的.故当时间t=0时,有：

u(0,a,z)=0 (0≤z≤Lr)

(13)

并且温差在有限时间内是有界的，故W(z)R(r)是有界的，由(12)式知其解析函数W(z)在定义域0≤z≤Lr是有界的，因此R(r)在解空间中也必有界.但在解(11)中(图1)，容易知第二类Bessel函数Y0在0点是无界的，故在此物理背景下，只能取q1=0,才能使解与真实的物理背景相吻合，所以方程(9)满足条件的解应为：

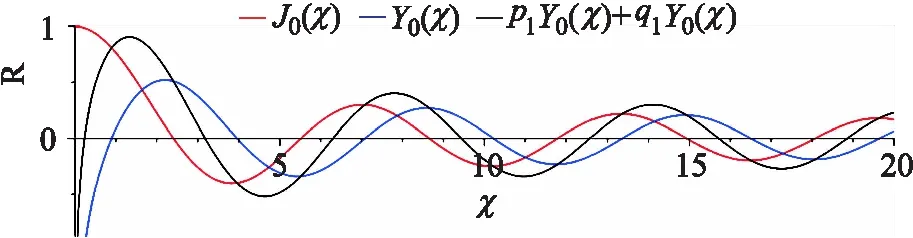
图1 解(11)以及0阶的两类Bessel函数图像Fig.1 Graph of the solution (11) and two kinds of 0-order Bessel functions

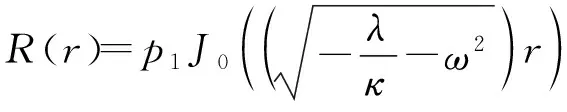
(14)

再由(13)式知：

u(0,a,z)=W(z)R(a)=0(0≤z≤Lr).

显然W(z)不恒等于零，故推知：

R(a)=0

(15)

联合(14)与(15)，易知：

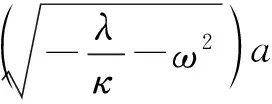
β1<β2<β3<…<βj<…,

故必存在一个j，使得

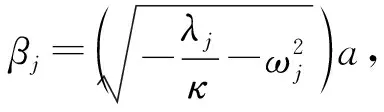
(16)

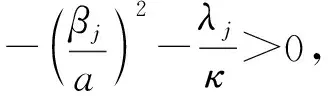
(17)

由于方程(9)是线性方程，由(14)式知方程(9)有无穷多个解：

(18)

其中j=1,2,…,n.同理，由(12)式知方程(10)也有无穷多个解：

Wj(z)=W(z)=p2cosωjz+q2sinωjz

(19)

其中j=1,2,…,n.从而方程(1)的任意一个解可表示为:

(20)

其中Aj、Bj为任意常数.根据解的叠加原理，方程(1)的一般解是无穷多个解的线性组合：

(21)

在以上过程中，仅讨论了边界条件下解的情况，所以系数Aj、Bj、λj为任意常数.如果要获得符合实际问题的特解，需要确定这些常数，那就需要给定初值条件.接下来，来讨论方程(1)满足某些初始条件的解，即如下通过初值条件确定系数Aj、Bj、λj.假设方程(1)满足下列初始条件和边界条件：

u(0,r,0)=f(r),0≤r≤a

(22)

uz(0,r,z)|z=0=g(r),0≤r≤a

(23)

(24)

由解(21)及初值条件(22)知：

(25)

再由傅里叶-贝塞尔展开式的性质知，相应的贝塞尔系数可表为：

(26)

又由解(21)及初值条件(23)知：

(27)

所以：

(28)

再由解(21)及初值条件(24)可推知：

从而，相应的贝塞尔系数可表为：

(29)

因此，满足以上初值条件的特解的相应系数Aj,Bj,λj可由(26)、(28)和(29)式来共同确定，当n→+∞时，方程(1)的精确形式的特解形式就是(21)式，但也仅仅只是一个形式而已.

实际上，由于j是一切自然数，故也无法通过这种方式获得方程(1)的精确形式的特解，但可以通过(21)、(26)、(28)和(29)式来获得一定精度的n次近似解：

(30)

为了能够直观地展示以上解所蕴含的物理现象，以解(20)为例，当j=1时，分别在参数值为A1=B1=10,a=1,κ=0.02,λ1=-1,β1=5.52,α=0.25的情况下，在不同的空间区域绘出它的动力学图像，见图2.

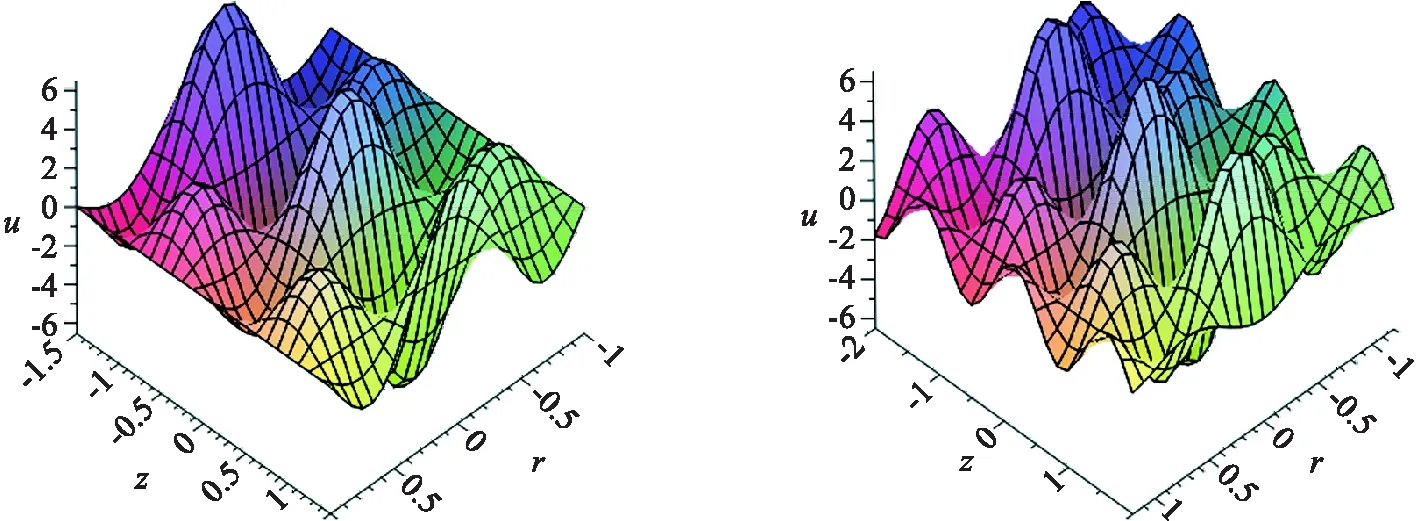
(a) t=1,r∈[-1,1],z∈[-1,1] (b) t=1,r∈[-1.5,1.5],z∈[-1.5,1.5]

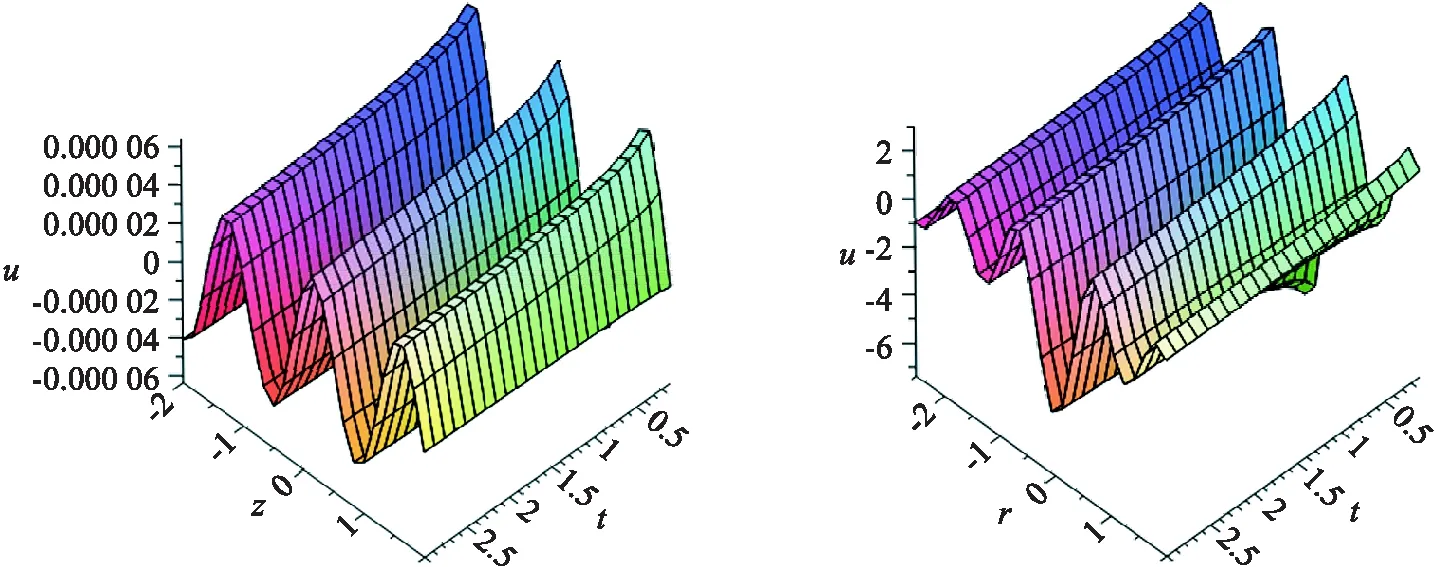
(c) r=1,t∈[0.1,3],z∈[-2,2] (d) z=1,t∈[0.1,3],r∈[-2,2]图2 解(20)随时间和空间演化的三维动力学坐标图Fig.2 Dynamic 3D-graph of the solution (20) evolving over time and space

图2中(a)和(b)两图展示的是温度在空间(r,z,u)中的发展变化规律，非常明显，温度在此空间中呈周期性变化，而且随着平面区域(r,z)的扩大，振幅在衰减.图2中(c)和(d)两图展示的是温度分别在空间(t,z,u)和(t,r,u)中的发展变化规律，同样地，温度在这空间中也呈周期性变化，而且随着时间的增加，振幅也都在衰减.只是从图2(c)可以看出，温度沿着z轴方向(沿转子长度方向)的变化很小，没有沿着r轴方向(沿转子半径方向)的变化那么明显.实际情况正是如此，由于温度主要是由于转子旋转时的摩擦所引起的，所以沿半径方向的热交换比较激烈，而整个转子都浸泡在液体中，整个转子在同一层面各段的温差变化应该不大.

情形2σ>0的情形

若σ>0不妨令σ=m2(m≠0),此时方程(8)可化为下列两个变系数的二阶线性常微分方程：

(31)

W″(z)-m2W(z)=0

(32)

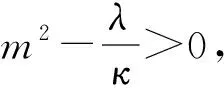
(33)

其中：p3、q3为任意常数，J0、Y0分别表示0 阶的第一类和第二类Bessel函数.

易知方程(32)的通解为：

W(z)=p4emz+q4e-mz

(34)

其中p4、q4为任意常数.由于Y0在0附近是无界，为了让解与实际的物理现象相吻合，故在(33)式中只好选择q3=0,于是方程(31)与实际的物理现象相吻合的解应为：

(35)

类似于前面(15)式的讨论，此时也有R(a)=0,即：

(36)

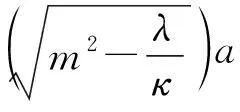
(37)

从而，方程(31)有无穷多个解：

(38)

把(37)代入(32)得：

(39)

再把(38)和(39)代入(4)，获得方程(1)满足边界条件R(a)=0的任意一个解：

(40)

其中Pn、Qn为任意常数.由解的叠加原理知，方程(1)在上述条件下的一般解可表示为：

(41)

类似地，利用上面给定的初始条件，其特解的系数应满足下列等式：

情形3σ=0的情形

若σ=0时，方程(8)可化为下列两个二阶线性常微分方程：

(42)

W″(z)=0

(43)

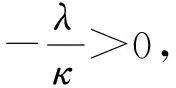
(44)

其中p5、q5为任意常数，J0、Y0分别表示0阶的第一类和第二类Bessel函数.

易知方程(43)的通解为

W(z)=p6z+q6

(45)

其中p6、q6为任意常数.同样地，由于Y0在0附近是无界的，故在(44)式中选择q5=0,于是，方程(42)的解变为：

(46)

类似于前面的讨论，易知方程(42)满足边界条件R(a)=0的解有无穷多个，可表为：

(47)

类似于前面讨论：

(48)

其中k为任意自然数.此时方程(1)的任意一个解可表示为：

(49)

其中Ak、Bk为任意常数.再由解的叠加原理知，方程(1)在上述条件的一般解可表示为：

(50)

且满足上述初始条件的特解的相关系数可由下列等式确定：

3 结 论

本文利用单参数Mittag-Leffler函数的分数阶导数性质，结合一种半固定式的变量分离法研究了2+1维的时间分数阶热传导方程(1)，在Bessel方程的解及其相关性质的帮助下，获得了该模型的三类精确解的一般表达式.在不同的初值条件和边界条件下，给出了相应的特解的计算办法，然后通过解的三维坐标图形直观地展示了解(20)随时间变量和空间变量演化的物理学现象，从而揭示了模型所蕴含的温度变化规律.在初值条件下，尽管给出了确定特解的系数的计算方式，但由于系数有无穷多个，实际上无法利用这种方式获得特解的精确表达式，但可以像(30)式那样获得n次近似解的精确表达式.