尾缘襟翼偏转角对不同翼型的垂直轴风力机气动影响研究
戴孟祎, 张志豪, 涂佳黄, 韩兆龙, 周 岱, 朱宏博
(1. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240;2. 湘潭大学 土木工程学院, 湖南 湘潭 411105)
近年来,风能以其清洁的特性、丰富的储量以及日趋成熟的风力发电技术,成为未来最具前景的新能源形式之一[1].风力机作为捕获风能的重要装置,其构型对于提高风力机的风能转化率、降低生产和运行维护成本具有重要意义[2].与传统水平轴风力机相比,垂直轴风力机具有设计简单、对风向不敏感等优点[3],但垂直轴风力机较低的风能利用率成为了其大规模商业化应用的瓶颈.
在旋转过程中,垂直轴风力机叶片的攻角会出现周期性变化,当叶片的攻角超过失速攻角时,叶片表面气体就会流动分离,从而使得叶片的气动性能急剧下降[4].因此,研究人员提出利用不同的流动控制手段改善叶片的气动性能.流动控制手段主要可分为被动控制[5-7]和主动控制[8-10]两大类.其中,可变尾缘襟翼技术作为一种常见的主动控制手段,可通过改变翼型改变叶片的气动性能.
Chen等[8]通过对比固定浆距和变桨距垂直轴风力机的性能,发现叶片在旋转过程中做适当幅度的俯仰运动,能够有效抑制功率输出、转速和转矩输出的波动,并提高风力机的功率系数.Li等[9]为探索最优桨距控制空间解,搭建由遗传算法和计算流体力学(CFD)仿真模块组成的变桨距自动优化平台,得到能在较广的叶尖速比范围内使风力机平均功率系数均得以提升的优化叶片浆距.向斌等[10]为减小动态失速对垂直轴风力机气动性能的影响,提出在翼型尾缘处布置动态格尼襟翼的主动控制方法.研究结果表明,采用主动式格尼襟翼提高了垂直轴风力机的运行稳定性,并增大风力机在低风速下的启动力矩.缪维跑等[11]对NACA0012两段式襟翼翼型进行数值模拟,利用弦线变换得到襟翼摆角与攻角的关系,发现襟翼翼型在静态条件下由摆角引起的攻角迁移现象.研究结果表明,随襟翼摆角增大,有效攻角范围减小,翼型攻角产生迁移,受力亦发生变化.祖红亚等[12]以NACA0018为基准翼型,采用数值模拟方法研究尾缘襟翼相对长度对翼型气动性能的影响.研究结果表明,襟翼对翼型周围主涡发展和变化具有影响,不仅改善了翼型的失速特性,同时也提高了翼型的气动性能,襟翼翼型的失速攻角在研究范围内均大于基准翼型.
上述研究均是针对某一特定翼型下襟翼对叶片或风力机气动性能的影响所展开.然而,对于不同的翼型,襟翼对叶片和风力机气动性能的影响存在一定差异.因此,针对不同翼型下带有尾缘襟翼的风力机进行气动性能分析和优化设计具有重要工程意义.
本文采用计算流体动力学数值模拟方法,建立添加分离式尾缘襟翼的H型垂直轴风力机二维模型,基于NACA0018、NACA0021和NACA0024共3种基础翼型与-16°、-8°、0°、8°、16°共5组襟翼偏转角参数,从风能利用率、叶片气动力系数、风力机荷载和流场分布等方面对比分析了尾缘襟翼对不同翼型的H型垂直轴风力机的气动性能影响,为进一步研究和提高H型垂直轴风力机气动性能提供参考.
1 计算模型和方法
1.1 几何模型
采用文献[13]研究的三叶片H型垂直轴风力机作为原始模型,具体模型如图1所示.该垂直轴风力机使用NACA0021对称翼型,弦长c=85.8 mm,风轮旋转直径D=1 030 mm,转轴直径为c/6,自由来流速度U∞=9 m/s,叶片安装角为0°.3个叶片在同一个平面内,叶片长度l=1.456 4 m, 互为120°夹角.风力机模型的展弦比(叶片长度与弦长之比)接近17,相对较大.根据Rezaeiha等[14]的结论,该风力机叶片的三维效应对叶片中部截面影响不显著,适用于二维CFD模拟.因此,为减小计算量,本研究使用二维CFD模拟.为提高计算效率,忽略支撑杆对风力机整体性能的影响.
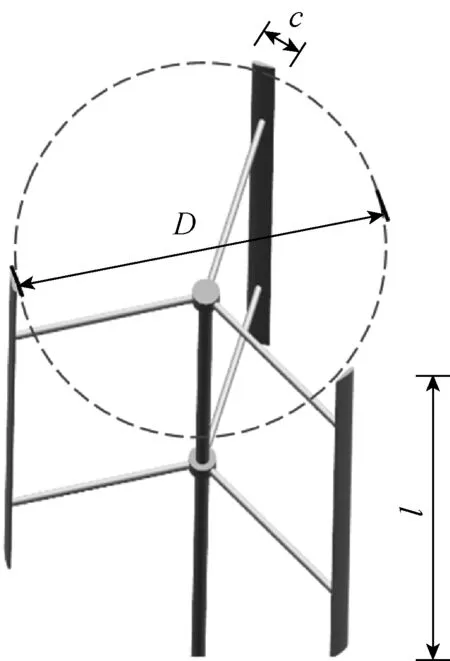
图1 原始H型垂直轴风力机3D模型Fig.1 3D model of original H-type VAWT
图2为风力机的旋转示意图.其中,α为叶片相对局部速度与弦线之间的夹角,即攻角;R为风轮旋转半径;ω′为角速度;FT为叶片所受切向力;FN为法向力;FL为升力;FD为阻力.假定顺风区的自由来流速度与逆风区的自由来流速度相同[15],即不考虑流动诱导的影响,相对局部速度可表示为
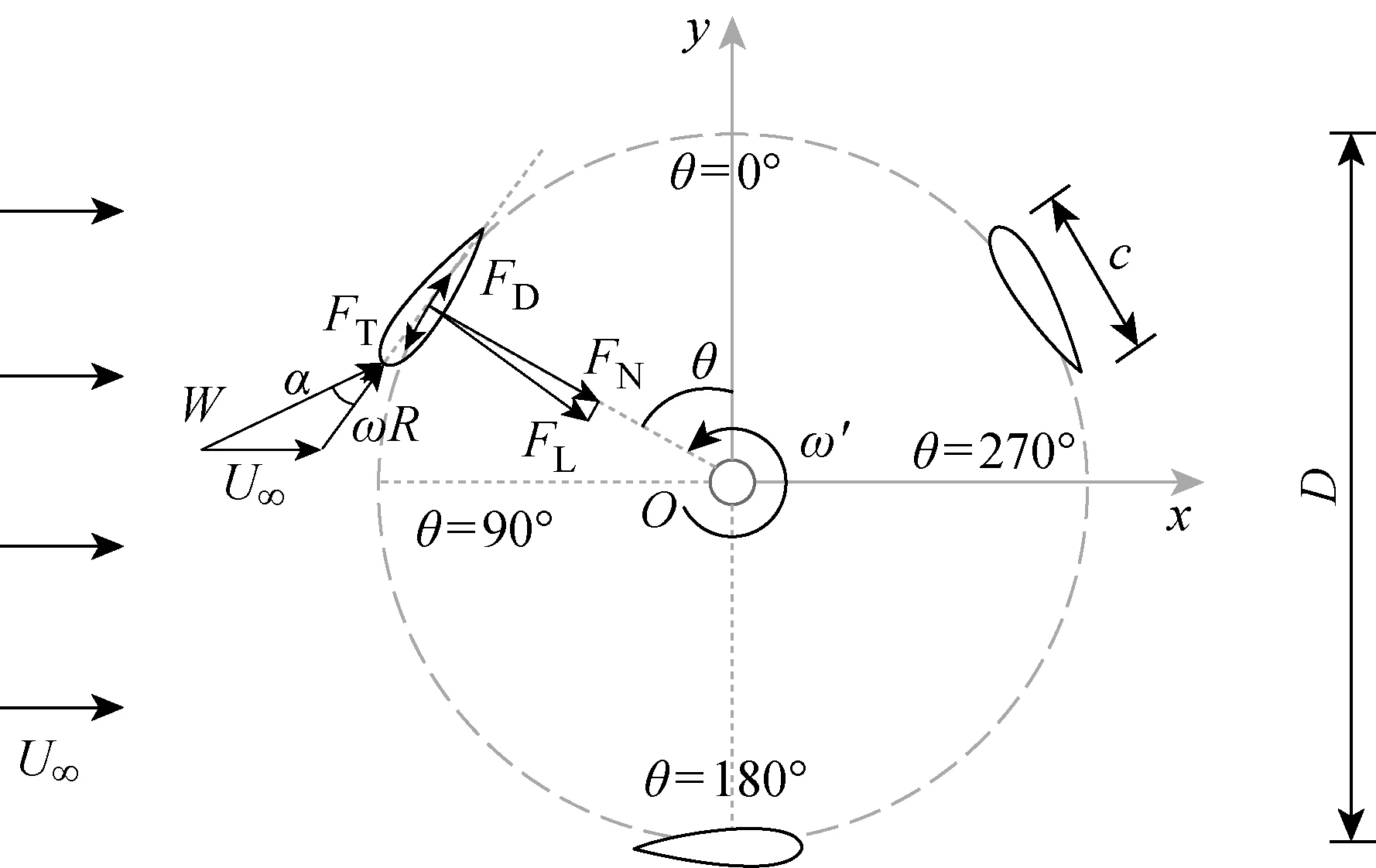
图2 风力机旋转示意图Fig.2 Schematic diagram of wind turbine rotation
(1)
式中:λ为叶尖速比;θ为叶片所在方位角.
攻角可表示为
(2)
根据叶片所在方位角θ的不同,将风轮旋转区域划分为逆风区(45°≤θ<135°)、背风区(135°≤θ<225°)、顺风区(225°≤θ<315°)和向风区(315°≤θ<45°)4个区域.功率系数Cp可由单叶片的弯矩系数Cm决定.
Cp=CmNλ
(3)
(4)
式中:N为叶片个数;M为风力机弯矩;ρ为空气密度;AC为参考面积.
此外,选取切向力系数CT、法向力系数CN、推力系数Cth和侧向力系数Cla共4个关键气动力参数,对作用在叶片上的气动力进行分析.
(5)
(6)
(7)
(8)
式中:H为叶片沿展向长度;Fth为叶片所受推力;Fla为侧向力;A为风力机的扫风面积.在二维计算中,FT、FN、Fth和Fla可根据计算软件监测到的叶片x和y方向上的力Fx和Fy与方位角θ的关系计算得到.
在原始模型的基础上,建立添加分离式尾缘襟翼的垂直轴风力机几何模型,叶片结构如图3所示.叶片弦长与原始模型的弦长相同,为c=85.8 mm.将叶片前缘至襟翼旋转中心的距离定义为主翼长度c1,襟翼旋转中心至叶片尾缘的距离定义为襟翼长度c2,主翼与襟翼的间隙定义为翼缝宽度d.参照祖红亚等[16-17]的工作,设置襟翼长度为0.3倍弦长,即c2=0.3c,设置翼缝宽度d=1.7%c.为了研究不同襟翼偏转角对垂直轴风力机气动性能的影响,襟翼偏转角β可绕其旋转中心在 ±16° 范围内偏转,定义偏转角为正表示襟翼向上偏转,偏转角为负表示襟翼向下偏转.
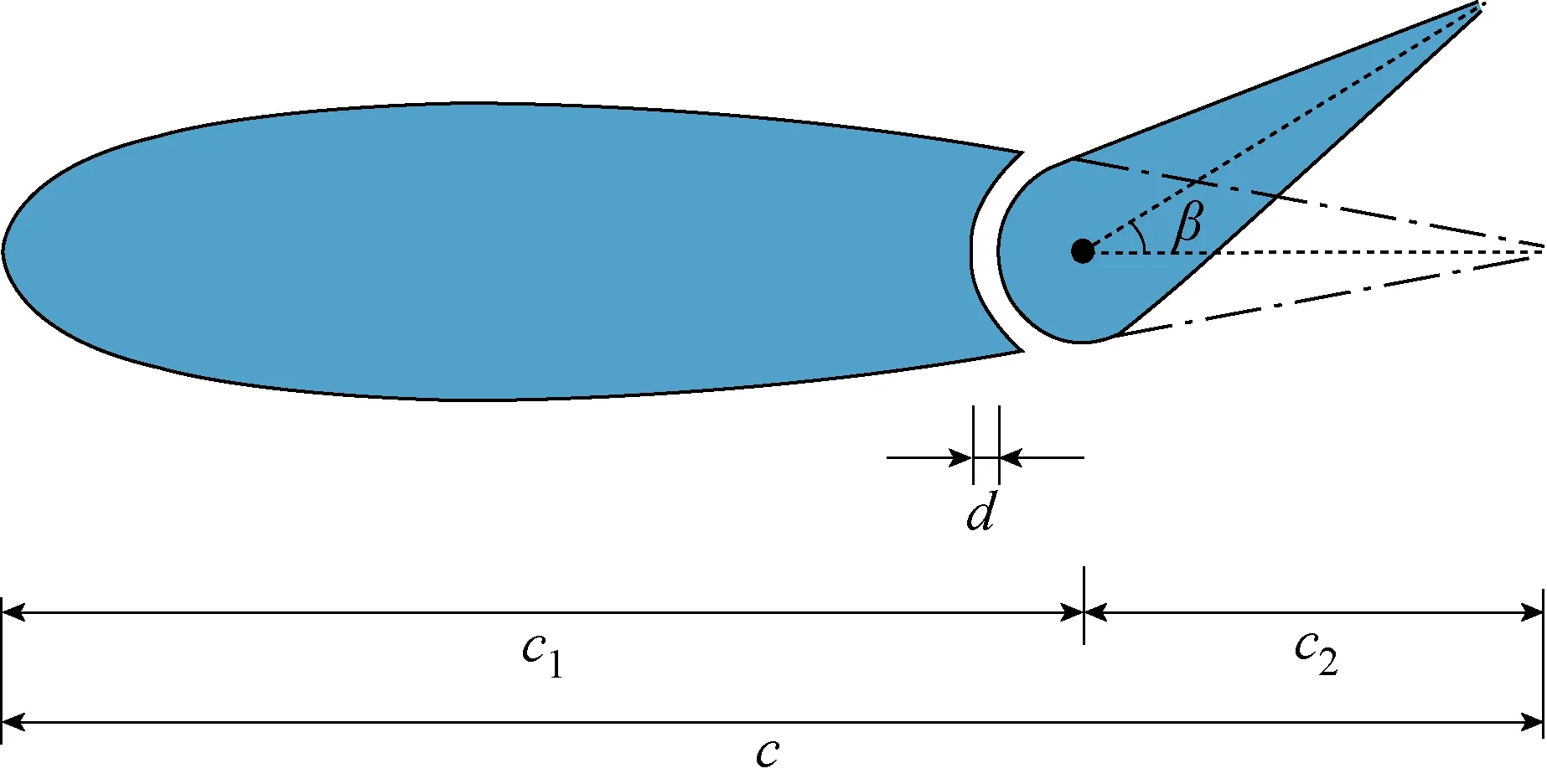
图3 分离式尾缘襟翼叶片示意图Fig.3 Schematic diagram of blade with separated trailing edge flap
1.2 数值方法
运用以有限体积法为基础的商业软件Fluent对垂直轴风力机气动性能和流场特性进行分析.考虑到风力机的性能在很大程度上取决于叶片边界层的发展,因此对转捩点的准确预测至关重要.采用4方程转捩剪切应力输运(SST)湍流模型求解纳维-斯托克斯(N-S)方程.转捩SST湍流模型除了使用k-ωSST湍流模型中采用的湍流动能和耗散率方程外,还结合另外两个考虑间歇因子γ和当地转捩雷诺数Reθ t的输运方程[18-19].其优点在于,一方面避免了一般情况下对平均场进行积分的过程,计算周期短且计算要求较低;另一方面对自由来流湍流度、分离和压力梯度等影响转捩的因素敏感,可以更准确地捕捉层流到湍流之间的过渡[20-21].
间歇因子表示在转捩区某一固定点流动处于有脉动和无脉动状态的时间比例,其输运方程为
(12)
式中:t为时间尺度;μ为动力黏度系数;Uj为y轴方向的速度分量;xj为y轴方向的位移分量;μt为转捩常数;S为应变率;Fle为转捩长度函数;Fon和Ftu为转捩控制函数;Ω为涡量;ca1、ca2、ce2和σγ为转捩常数.
(14)
式中:混合函数Fθ t为边界层中关闭源项;cθ t和σθ t为转捩常数.
在垂直轴风力机非定常气动特性的计算过程中,计算时间步长设置为T/1 440,其中,T为一个旋转周期的时长.确保数值模拟过程中风力机转子每转动0.25°进行一个时间步计算.单次时间步长包含20次迭代,保证模拟的湍动能残差ξ始终控制在ξ=10-6附近波动.基于Rezaeiha等[14]的研究结果,湍动能残差控制为ξ=10-6可以兼顾模拟的时间复杂度和结果精确度.整个模拟过程设置为20个周期,总时长Tmax=2.72 s,前10个周期的初始化及流场发展可以保证模拟结果的充分收敛,第11~20个周期的模拟用于分析风力机气动性能的相关参数.
2 计算域及有效性验证
2.1 计算域和网格分布
计算流体动力学分析要求高精度流场,本文建立的二维模拟区域保证流场内流体能够充分发展.为减小进出口边界和侧边界对计算精度的影响[22],将风力机布置在靠近上游的位置,入口到旋转中心的距离为10D,旋转域直径为1.5D,计算域沿入流方向的长度为30D,宽度为20D.模型的阻塞比(在二维计算中定义为风轮直径与计算域宽度之比)为5%,由对称边界条件导致的流动加速非常微弱,对风力机计算空气动力学性能的影响可以忽略[23].在计算中,忽略连接杆件的影响,将整个流场分成4个区域:外流域F、转轴控制域Z1、环形旋转域Z2和叶片控制域Z3,各区域之间设置交界面,通过滑移网格技术实现风轮旋转,具体计算域划分如图4所示.考虑叶片表面的粗糙度和扰流效应,叶片布置为无滑移壁面.边界设置为前端速度入口U∞=9 m/s.为了统一模型参数的计算与分析,湍流强度设置为3%.空气密度ρ=1.225 kg/m3,动力黏度μ=1.789 4×10-5Pa·s,压力出口为0 Pa,基于弦长的雷诺数Re=5.28×104.
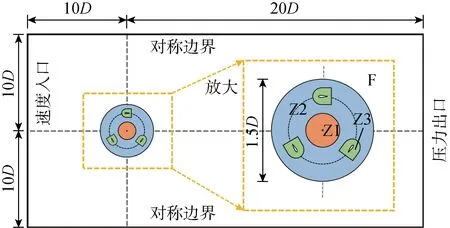
图4 计算流场区域划分Fig.4 Division of computational flow field region
为保证旋转域与外流场的良好过渡和下游流场的充分发展与稳定,对外流域的网格以旋转轴为中心进行十字形加密处理,加密宽度为3D,促进实现流场的进一步精确模拟.分别采用二维结构网格与非结构网格进行拓扑,转轴控制域Z1和外流场域F采用结构网格,环形旋转域Z2和叶片控制域Z3采用非结构网格进行网格加密,贴近壁面处使用边界层网格,首层网格高度设置为 0.01 mm,网格增长率为1.2%,使叶片壁面处y+≈1,以满足准确刻画边界层流动的要求.详细网格布置如图5所示,单个叶片控制域网格数约为17万,总网格数约为68万.所有仿真计算都在配置为Intel(R) Xeon(R) CPU E5-2676 V3@2.4 Hz的小型服务器上进行,一个计算周期大约需要消耗1 h,约20 h完成一个算例.

图5 计算域的网格拓扑Fig.5 Mesh topology of computational domain
2.2 网格独立性测试
网格质量通常对模拟结果的准确性有显著影响.因此,在正式计算前,进行网格独立性测试.改变叶片的最小表面尺寸,共设置3类网格方案,分别为粗网格、中网格和细网格.对叶尖速比λ=2.64时不同网格方案计算的功率系数进行比较,具体网格设置和结果如表1所示.
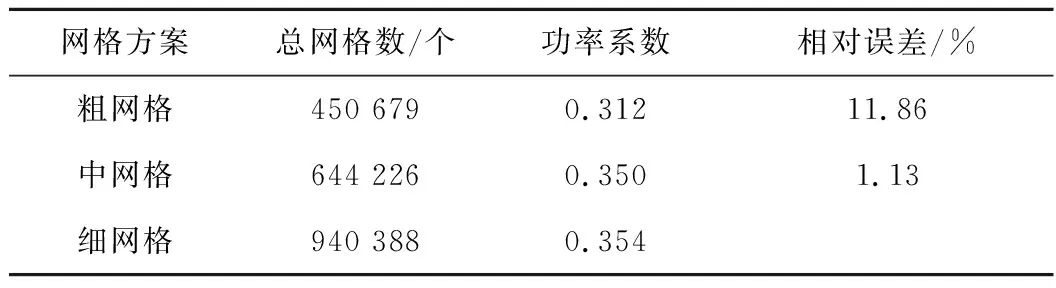
表1 基于功率系数误差的网格独立性测试Tab.1 Mesh independence test based on errors of power coefficient
结果表明,细网格和中网格方案的功率系数差别非常小,分别为0.354和0.350,但两者的总网格数量相差较大,约19万网格.另一方面,粗网格方案虽然网格数更少,但计算得到的功率系数的相对误差较大.需要注意的是,网格数量越多并不意味着结果越准确,因为还会受网格形状和分布的影响.因此,综合考虑计算时长与计算精度的要求,本研究基于中网格方案来执行其他仿真.
2.3 模型有效性验证
为评估CFD计算结果的准确性,选用文献[13]的实验结果与当前数值模拟结果进行对比验证.该实验数据已被广泛用于研究垂直轴风力机的气动性能[24-25],计算结果与实验数据对比如图6所示.
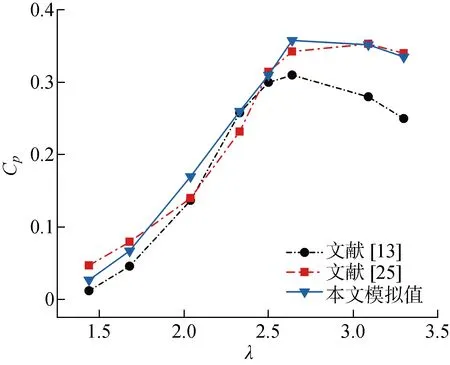
图6 现有结果与实验和数值数据对比Fig.6 Comparison of current results with experimental and numerical data
可知,在叶尖速比λ达到额定叶尖速比2.64前,功率系数Cp随λ增大而增大;而λ达到2.64后,功率系数Cp随λ增加呈减小态势.在低叶尖速比下,数值模拟的结果较好地表现了功率系数Cp随叶尖速比λ变化的趋势,而在高叶尖速比时,数值模拟结果对风力机的功率系数存在一定的高估,这与文献[25]中的数值计算结果类似.在高叶尖速比下,Cp被高估主要有两个原因:一是在二维CFD模拟中忽略了叶片高度,无法描述叶片两端的局部流动特征,不存在叶片尖端损失;二是由于CFD模拟过程中的几何简化与建模,例如叶片辐条和连接至风力机塔架的支撑杆会导致较大的阻力,并降低风洞测量时的风力机性能,而这些在本研究的数值模拟中被忽略.相关研究表明,由于支撑臂摩擦而导致的风力机性能损失可以达到20%左右,在高叶尖速比下,这一损失将更明显[13, 15].对于低叶尖速比(存在动态失速),由于几何简化,同样存在类似高估的问题.而在中等叶尖速比下,可能由于二维转捩SST湍流模型无法准确模拟风力机气动效应的固有三维流动复杂性,使这种预期的高估被抵消一部分.
总之,本文所采用的数值模型能够较好地反映垂直轴风力机在风洞中的气动特性,准确地再现实验结果.因此,目前的数值模型可以作为后续研究的一种可靠模拟方法.
3 结果与分析
NACA对称翼型族具有较高的升阻比和良好的失速特性,在H型垂直轴风力机的叶片选型上得到了广泛应用.本文选用3种不同厚度的基础翼型NACA0018、NACA0021和NACA0024,作为不同H型垂直轴风力机的叶片主体,叶片弦长与原始风力机模型的弦长一致.为分析尾缘襟翼对不同垂直轴风力机气动性能的影响规律,针对添加分离式尾缘襟翼的3种基础翼型NACA0018、NACA0021和NACA0024,分别选取襟翼偏转角为 -16°、-8°、0°、8°和16°的5种情况,取原风力机模型的额定叶尖速比2.64进行计算模拟,讨论风力机叶片的气动性能与叶片附近区域的流场特性.
3.1 气动性能与气动荷载
叶片弯矩系数Cm是决定风能利用系数Cp的关键参数.图7给出了翼型为NACA0018、NACA0021和NACA0024共3种垂直轴风力机在不同襟翼偏转角下单个叶片的弯矩系数随方位角的变化.可知,在逆风区,正向襟翼偏转角能够有效提高叶片的弯矩系数,且β=16°时,叶片的瞬时弯矩系数达到最优,此时NACA0018风力机的最大弯矩系数由0.179提高至0.246,增长了37.4%,NACA0021和NACA0024风力机的最大弯矩系数也分别增长了25.7%和30.4%.原因是在此方位角区间内,正向偏转的襟翼增大了叶片的有效攻角,使叶片升阻比得到提升.同样,在顺风区,负向襟翼偏转角对叶片的瞬时弯矩系数产生有利影响,且在β=-16° 时弯矩系数达到最优.考虑到中等叶尖速比下的垂直轴风力机本身气动性能较优,并不存在较严重的动态失速问题[26],因此可知,在其他区域,襟翼偏转角的提升效果有限,甚至低于无偏转时的风力机模型,对叶片弯矩系数造成不利影响.
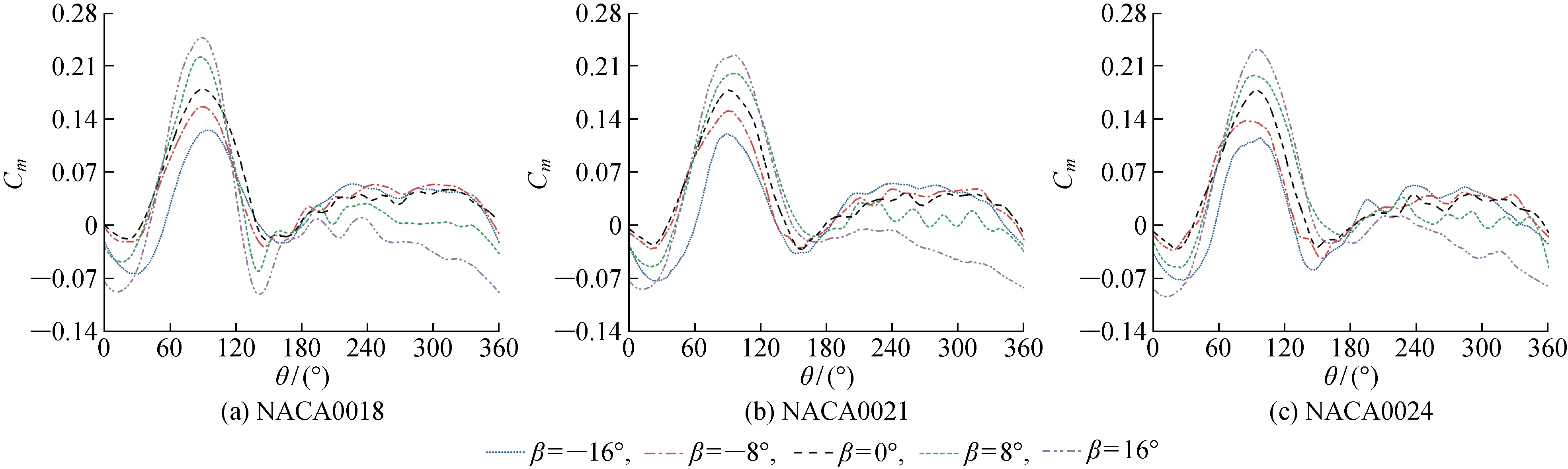
图7 不同襟翼偏转角下风力机的单叶片弯矩系数Fig.7 Moment coefficient of blade at different flap angles
单个叶片的切向力系数和法向力系数对比分别如图8和图9所示.切向力方向与叶片绕旋转轴旋转的切线方向相同为正;法向力垂直于叶片绕转轴旋转的切线,指向风轮旋转中心为正.与单叶片弯矩系数随方位角的变化相似,逆风区的正向襟翼偏转角和顺风区的负向偏襟翼转角可以使叶片的切向力系数得到提高,且β=16°时,叶片切向力系数在θ=90°处达到最大值.此时NACA0018风力机的最大切向力系数由1.757提高至2.532,增长了44.1%,NACA0021和NACA0024风力机的最大切向力系数也分别增长了30.6%和37.9%.

图8 不同襟翼偏转角下风力机的单叶片切向力系数Fig.8 Tangential force coefficient of blade with different flap angle
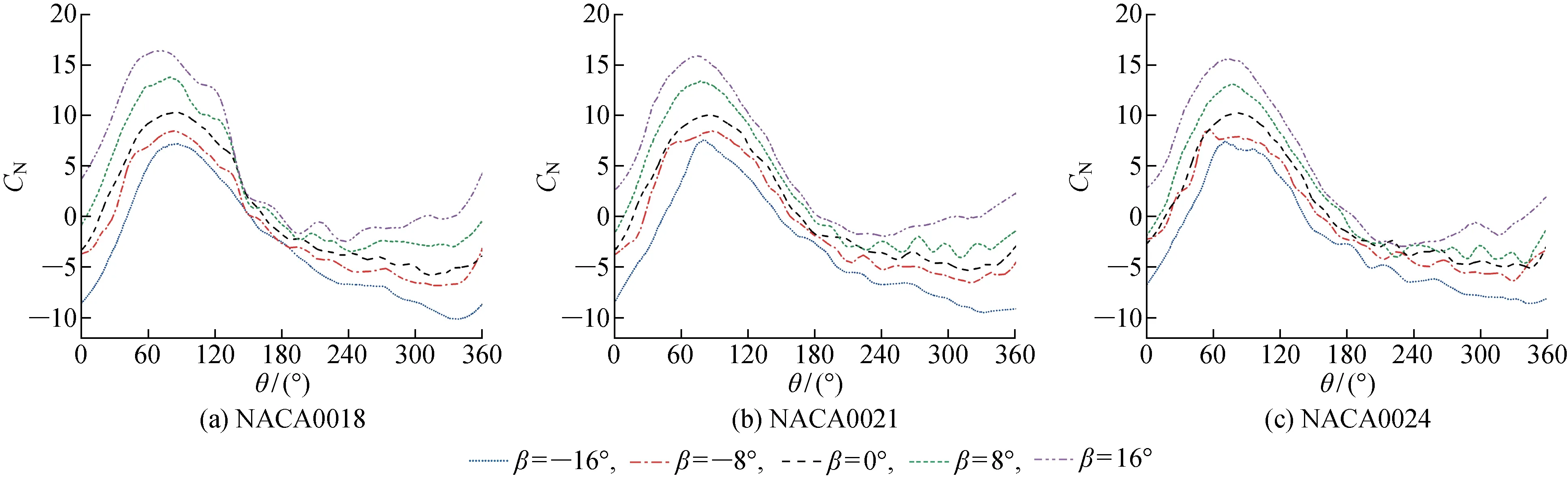
图9 不同襟翼偏转角下风力机的单叶片法向力系数Fig.9 Normal force coefficient of blade at different flap angles
从叶片的法向力系数对比可知,在整个旋转周期范围内,负向襟翼偏转角能够有效降低法向力系数.在β=-16° 时,叶片法向力系数在θ=90°处达到最大值.此时NACA0018风力机的最大法向力系数由10.310下降到7.202,降低了30.1%,NACA0021和NACA0024风力机的最大法向力系数也分别降低了24.6%和27.2%,表示风力机在旋转过程中支撑杆受到的荷载可以得到大幅降低.
不同垂直轴风力机在一个稳定的旋转周期内平均功率系数和平均弯矩系数的对比如图10(a)和图10(b)所示.显然,分离式尾缘襟翼的偏转角对风力机的动力性能有重要影响.对3种垂直轴风力机而言,在某些方位角区间内尾缘襟翼的偏转能够使风力机叶片的瞬时弯矩系数得到提高,但风力机整机的平均功率系数和平均弯矩系数均随襟翼偏转角的绝对值的增大而减小,说明简单地设置固定偏转襟翼并不能使整机动力性能得到明显改善,这与图7分析结果一致.
对于大型垂直轴风机的设计与运用,叶片周期性的转动将导致整机受到周期性的疲劳荷载,这些疲劳荷载是需要重点考量的因素.风力机的气动载荷是衡量其气动性能的主要参数,图10(c)和10(d)分别为不同垂直轴风力机在一个稳定的旋转周期内平均推力系数和平均侧向力系数的对比,推力和侧向力分别指风力机整体受到的沿来流方向的力和垂直于来流方向的力.可知,负向襟翼偏转角会在一定程度上降低风力机的推力系数;而偏转角为正时,推力系数随偏转角度的增大而增大.对于侧向力系数,整体呈现为随偏转角绝对值的增大而增大的趋势.说明单一地改变襟翼偏转角对改善风机整体荷载的作用效果不突出,与图8和图9的分析结果相符.
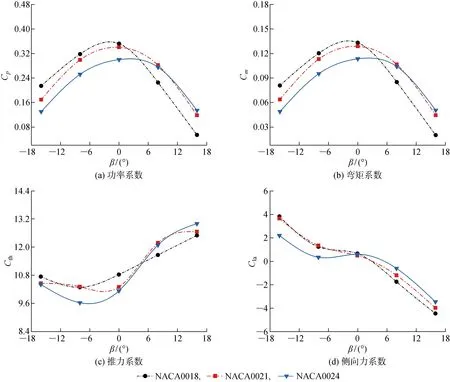
图10 不同垂直轴风力机的对比Fig.10 Comparison of different VAWTs
为进一步分析尾缘襟翼对不同厚度翼型的垂直轴风力机动力性能的影响,将各风力机在不同襟翼偏转角下的功率系数与β=0° 时的功率系数作差得到ΔCp,并求功率系数的变化率,即ΔCp/Cp(β=0°),可直观得到不同风力机ΔCp随尾缘襟翼的变化分布,如图11所示.对任意风力机而言,襟翼偏转角的绝对值越大,功率系数变化越明显,且变化速率逐渐增大.对比3种垂直轴风力机,当襟翼偏转角为负时,NACA0024风力机的功率系数随偏转角变化最明显,结合图10(a)可知,偏转角从0°减小至 -16°,其功率系数由0.301降低至0.129,下降了57.1%,NACA0021和NACA0018风力机的功率系数也分别下降了50.3%和39.2%;当襟翼偏转角为正时,NACA0018风力机的功率系数随偏转角变化最明显,偏转角从0° 增大至16°,其功率系数由0.352降低至0.054,下降了84.7%,NACA0021和NACA0018风力机的功率系数也分别下降了65.3%和55.3%.由此可见,在负向襟翼偏转角下,风力机功率系数受偏转角影响的程度与翼型厚度呈正相关;而在正向襟翼偏转角下,功率系数受偏转角影响的程度与翼型厚度呈负相关.
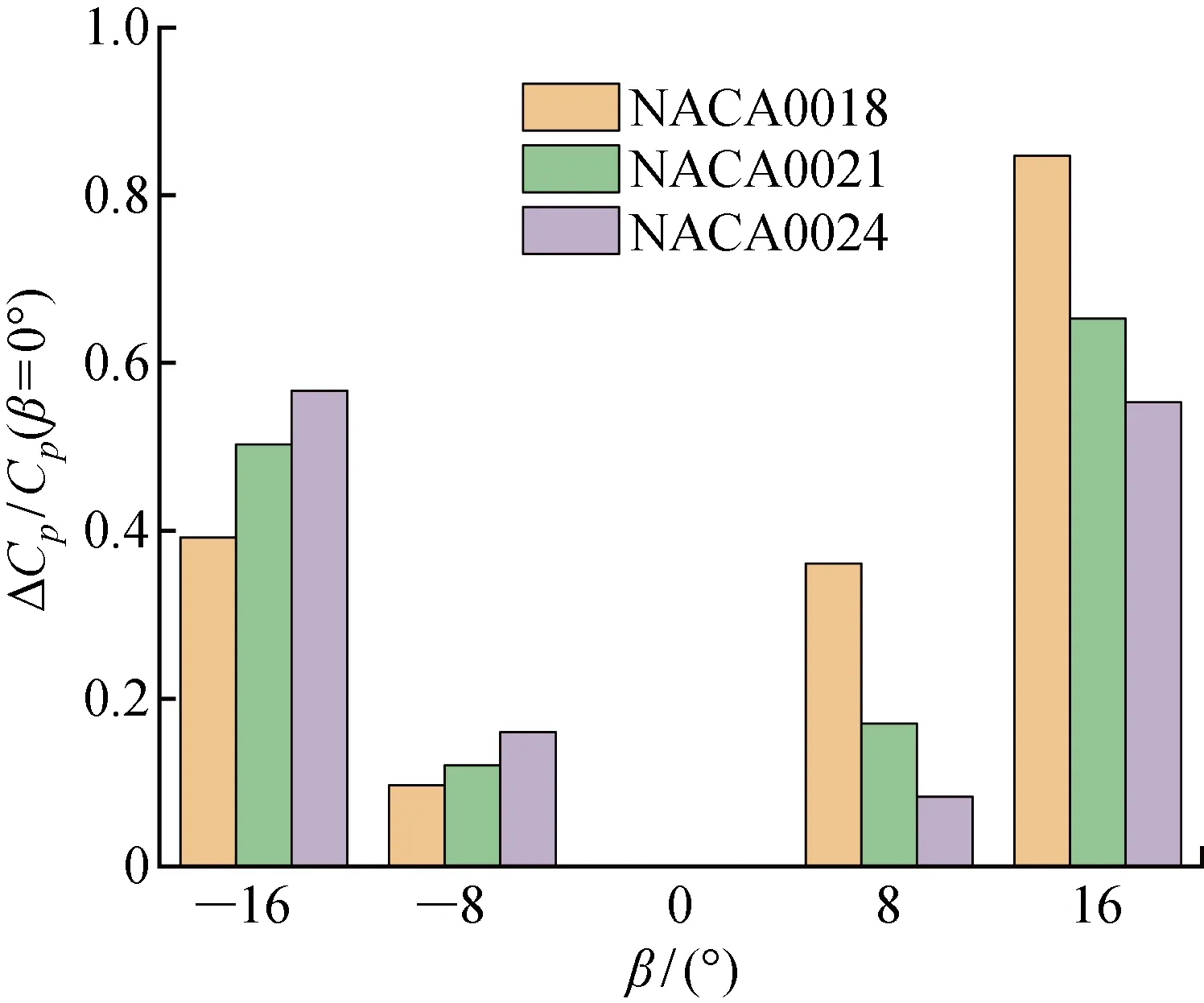
图11 不同垂直轴风力机ΔCp随尾缘襟翼变化分布Fig.11 Distribution of ΔCp with trailing edge flap deflection angle for different airfoils
3.2 流场分布
动态失速与叶片表面发生的流动分离直接相关[27].图12给出了NACA0018和NACA0024风力机在不同襟翼偏转角下翼型周围的涡量分布对比,以观察流动分离的形成和发展,并进一步解释风力机气动性能特性的内在机理.
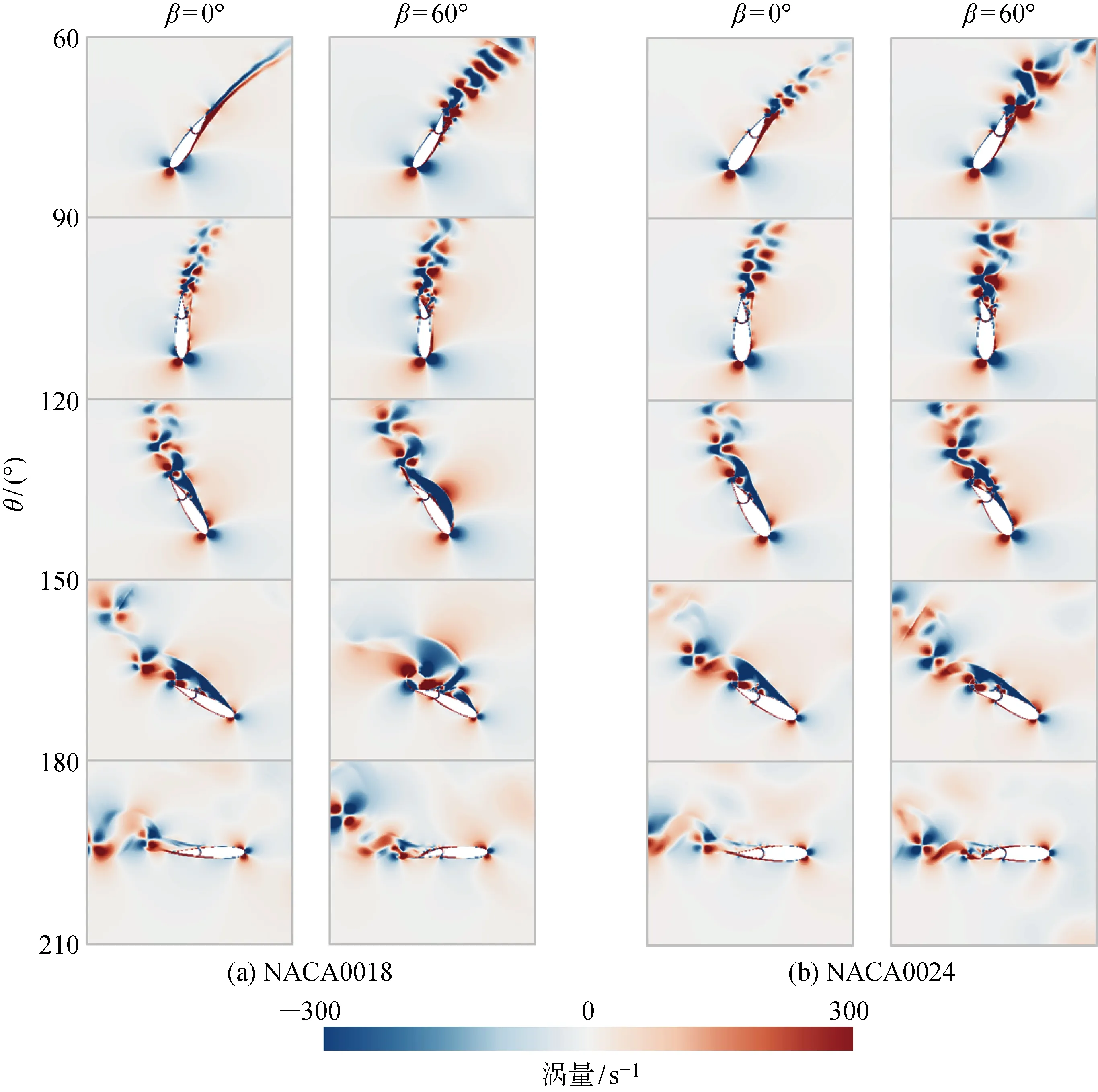
图12 不同风力机翼型周围的涡量分布对比Fig.12 Comparison of vorticity distributions around airfoil for different VAWTs
在方位角θ=60° 时,对于β=0° 的模型,NACA0018风力机的气流基本附着在叶片表面,未发生流动分离现象,而NACA0024风力机尾缘下游区域存在显著的周期性旋涡结构;对于β=16° 的模型,两种不同翼型工况下,襟翼的偏转导致襟翼处产生明显的流动分离,尾缘处形成周期性的卡门涡街.当叶片旋转到θ=90° 位置时,对于β=0° 的模型,由于攻角的增大,尾缘产生轻微流动分离,形成周期性尾涡.同时由于翼缝的存在,襟翼靠近翼缝的位置出现小尺度的涡;对于β=16° 的模型,襟翼的偏转延缓了尾缘处的流动分离,并使翼缝处的涡得到小范围扩散,解释了图7所示的叶片产生更大弯矩系数的结果.当叶片旋转到θ=120° 位置时,由于攻角增大,叶片表面的气流高度分离.后缘涡和前缘涡的强度大大增加,表明在这一阶段发生了严重的动态失速,对应图7中弯矩系数的急剧下降.在θ=150° 位置,由于攻角逐渐减小,从前缘产生的气流分离逐渐受到抑制,后缘产生的旋涡结构向下游处进一步发展.对于β=16° 的工况,叶片襟翼的偏转加剧了后缘附近处的流动分离.当叶片旋转到θ=180° 位置时,从叶片前缘和后缘脱落的涡逐渐消散,攻角在此位置再次归零,气流逐渐重新附着到叶片表面,流动分离强度减弱,因而导致图7中弯矩系数激增.对比不同方位角下,NACA0018和NACA0024风力机有无襟翼偏转工况下的涡量图可知,β=16° 的偏转襟翼对NACA0018风力机流场分布的影响比对NACA0024风力机的影响更显著,尤其在θ=120° 和θ=150° 的位置,这与图11得到的分析结果一致.
4 结论
针对添加尾缘襟翼的垂直轴风力机的空气动力学问题,采用计算流体动力学转捩SST湍流模型,开展3种不同分离式尾缘襟翼的翼型(NACA0018、NACA0021和NACA0024)叶片的H型垂直轴风力机气动性能的数值研究.对比不同襟翼偏转角 -16°、-8°、0°、8°、16° 下3种风力机模型的风能利用率、叶片气动力系数、风力机荷载和流场分布等结果,主要结论如下:
(1) 襟翼偏转角度变化能够导致风力机气动性能变化.在本文的研究模型中,与尾缘襟翼不发生偏转的模型相比,风力机的平均功率系数随襟翼偏转角的绝对值增大而减小.
(2) 在逆风区(45°≤θ<135°),正向襟翼偏转角可以有效提高叶片的弯矩系数,当β=16° 时,叶片的瞬时弯矩系数达到最优,NACA0018、NACA0021和NACA0024风力机的弯矩系数分别增长了37.4%、25.7%和30.4%;在顺风区(225°≤θ< 315°),负向襟翼偏转角对叶片的瞬时弯矩系数产生有利影响,在β=-16° 时弯矩系数达到最优.
(3) 对不同翼型的H型垂直轴风力机,当襟翼偏转角为负时,风能利用率受偏转角影响的程度与翼型厚度呈正相关,即NACA0024风力机受影响程度最大,在β=-16° 时风能利用率下降了57.1%;当襟翼偏转角为正时,风能利用率受偏转角影响的程度与翼型厚度呈负相关,即NACA0018风力机受影响程度最大,在β=16° 时风能利用率下降了84.7%.

