风力机翼型尾缘厚度对气动噪声的影响∗

曾明伍，孙振业，朱卫军，李松林

(1.东方电气风电有限公司,四川 德阳 618000；2.扬州大学 电气与能源动力工程学院,江苏 扬州 225127)

0 引言

随着风力机大型化发展，并逐渐接近人口密集区域，风力机产生的噪声问题日趋严重.传统风力机叶片多采用薄翼型，叶片横截面积小，承载能力有限.随着大厚度钝尾缘翼型的广泛使用[1]，钝尾缘对风力机的气动性能以及气动噪声起着不可忽视的影响.风力机噪声主要由两部分构成：机械噪声和气动噪声[2]，前者是由于机械设备工作时，部件和壳体产生振动所发出的[3]，后者是风力机噪声的主要部分[4]，包含低频噪声、湍流入流噪声、翼型自噪声.低频噪声是旋转叶片与塔架或风剪切相互作用产生，由于人耳对其不太敏感，所以在A加权噪声频谱图上，此类噪声对A加权声功率级贡献较少，湍流入流噪声是叶片与入流相互作用产生的.翼型自噪声主要包括尾缘噪声、叶尖涡噪声、钝尾缘噪声等[5].上述三种翼型气动噪声中，翼型自噪声占主导地位，而尾缘噪声是翼型自噪声的主要部分，因此研究尾缘厚度对翼型噪声的影响具有重要意义.

关于风力机气动噪声的研究主要通过实验及数值模拟实现,钝尾缘翼型的研究主要在气动性能方面，噪声的相关研究目前还比较少.朱卫军[6]将可压缩NS方程分离成不可压缩流动方程和无粘声学方程两个部分，使得计算噪声仿真计算效率得以提高；朱卫军等[7]介绍了一种基于二维声线理论的风力机旋转叶片气动噪声传播模型，该模型包括几何分布的衰减因子、声指向性、空气吸收、反射、折射以及温度和气流等.陈进等[8]提出了一种大厚度钝尾缘翼型优化设计方法，表明新翼型能同时提高叶片的气动和结构性能.李志伟[9]利用Fluent 软件对NACA0012直叶片进行了CFD仿真，分析了叶片尾缘区域及尾迹流场，采用FW-H方法和FFT变换，得到了叶片气动噪声的声场分布.刘雄等[10]以FFA-W3翼型族为研究对象，对其系列翼型的后缘进行了适当的加厚，对比分析了风力机的气动性能.任旺等[11]采用大涡模拟对DU91-W2-250翼型进行仿真，利用FW-H方法求解了远场噪声，分析了翼型尾缘厚度对噪声的影响，结果表明减小尾缘厚度能够降低翼型气动噪声水平.

为研究翼型尾缘厚度对气动噪声的影响，本文选取DU系列翼型作为研究对象，通过XFOIL计算翼型气动数据，采用修正BPM半经验模型仿真翼型气动噪声，研究翼型的尾缘厚度对气动特性和翼型气动噪声的影响.

1 模型

针对风力机气动噪声产生机理，Brooks，Pope和Marcolini提出了风力机翼型噪声预测半经验模型，简称BPM半经验模型[12].BPM半经验模型是对一组NACA0012翼型（弦长不同）进行大量的气动和声学测量总结得到的，其给出了风力机叶片翼型自噪声的五种半经验模型[13].在无大分离流动时，该模型进行噪声预测的速度和精度均可满足实际工程需要，因此得到大范围的应用.但不同的风力机叶片的翼型形状、弦长各不相同，来流情况也大不相同，因此由相同半经验公式来计算不同的翼型边界层参数，必然会导致一定的误差，因此需要对公式进行修正.基于半经验模型，Lowson研究了模型中所用到的边界层厚度.Moriarty等[14]对半经验预测方法进行改进，得到更加准确的风力机噪声预估，朱卫军等[15,16]基于翼型噪声预测半经验模型，引入叶素动量理论，在翼尖位置采用了一种新的翼尖修正技术，提高了模型的准确度.

1.1 湍流边界层尾缘噪声

在一定的条件下，翼型表面的某个位置会发生转捩，湍流会在尾缘产生压力波动.湍流边界层与尾缘相互作用产生湍流边界层尾缘噪声，如图1所示.在攻角较小时，湍流边界层尾缘噪声是翼型自噪声的主要部分.湍流边界层尾缘噪声由吸力面产生的噪声和压力面产生的噪声叠加而成，见公式（1）～（3）：

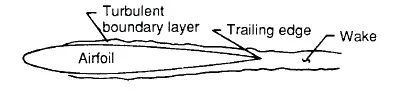
图1 湍流边界层尾缘噪声Fig 1 Turbulent boundary layer noise on trailing edge

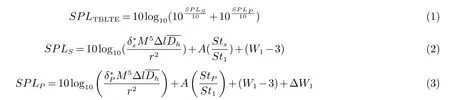
式中：SPLTBLTE为湍流边界层尾缘噪声的声压级；SPLS为翼型吸力面的声压级；SPLP为翼型压力面的声压级；分别为吸力面边界层位移厚度和压力面边界层位移厚度，与攻角α和雷诺数Re有关；M为马赫数；r为距观测者的距离；∆l为翼展为声指向性函数；St为斯特劳哈尔数；A为频谱形状函数；W1为振幅函数；∆W1为声压级修正函数.

1.2 分离流噪声

当攻角较大时，边界层发生分离，吸力面部分的湍流涡不断增大，边界层发生大规模分离，翼型处于完全失速状态，如图2所示.整个吸力面转捩成非定常流，此时分离流噪声是翼型自噪声的主要部分，表达式如下：

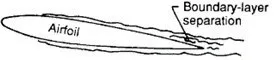
图2 分离流噪声Fig 2 Boundary layer separation noise

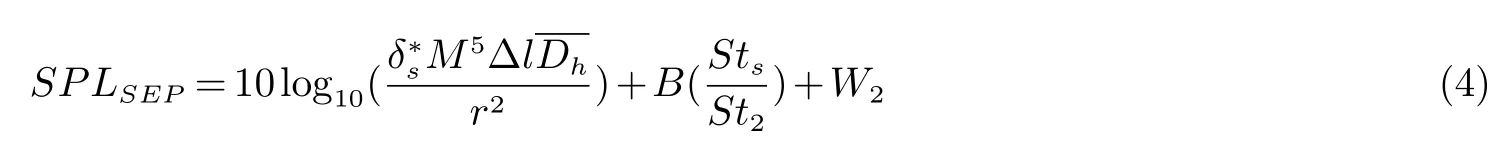
式中：B为频谱形状函数；W2为振幅函数.

1.3 层流边界层涡脱落噪声

尾缘的涡脱落以及上游层流边界层形成的不稳定循环产生了涡脱落噪声.当涡从尾缘脱离时，它引起的压力会传播到上游，从而导致边界层的波动；当不稳定的边界层波动达到尾缘，导致涡脱落，如图3所示.如此循环往复导致了层流边界层涡脱落噪声，表达式如下：

图3 层流边界层涡脱落噪声Fig 3 Laminar boundary layer vortex shedding noise

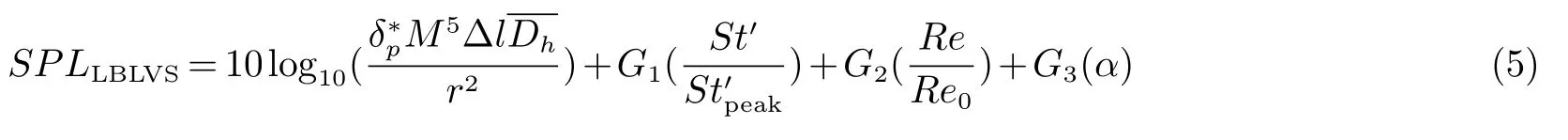
式中：G1、G2、G3为经验函数，与斯特劳哈尔数、雷诺数、攻角有关.

1.4 钝尾缘噪声

涡从钝尾缘处脱落，就会产生钝尾缘噪声，如果翼型尾缘厚度与它本身边界层厚度相差较大时，钝尾缘噪声是翼型自噪声的主要部分，如图4所示.由于钝尾缘噪声源的频率和振幅主要由尾缘的几何形状决定，一般可以通过减小尾缘厚度来降低噪声，表达式如下：

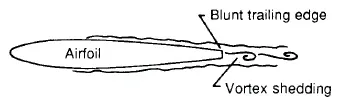
图4 钝尾缘噪声Fig 4 Blunt trailing edge vortex shedding noise

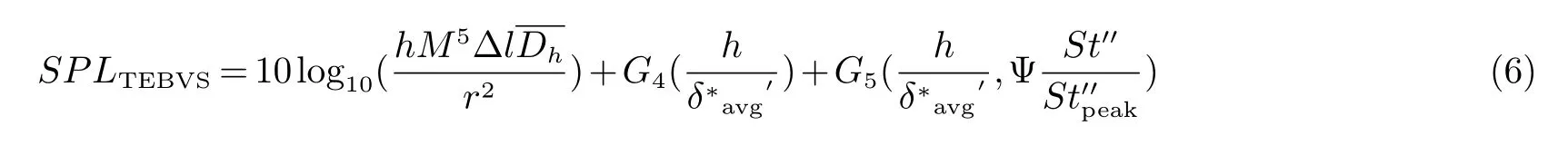
1.5 叶尖涡噪声

叶尖涡与叶尖作用会产生噪声，这种噪声和上述几种噪声的产生机理不同，本质上是由于三维流动形成的，如图5所示.叶尖涡噪声与叶尖的几何形状关系密切，可通过良好的叶尖几何外形设计来降叶尖涡噪声，表达式如下：

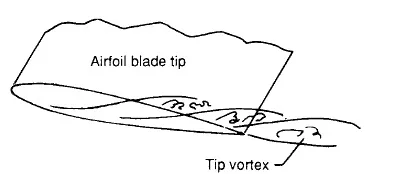
图5 叶尖涡噪声Fig 5 Tip vortex noise

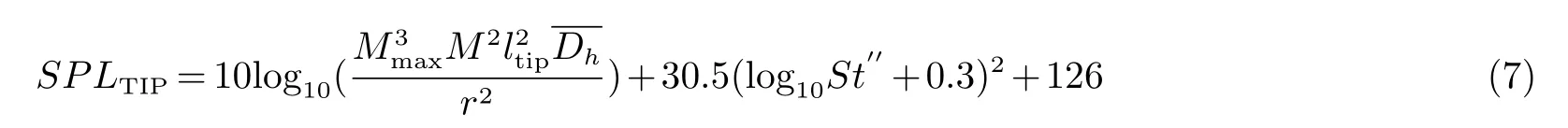
式中：Mmax为叶尖位置马赫数；ltip为叶尖沿展向的长度.

对于圆形叶尖：

对于扁平状叶尖：

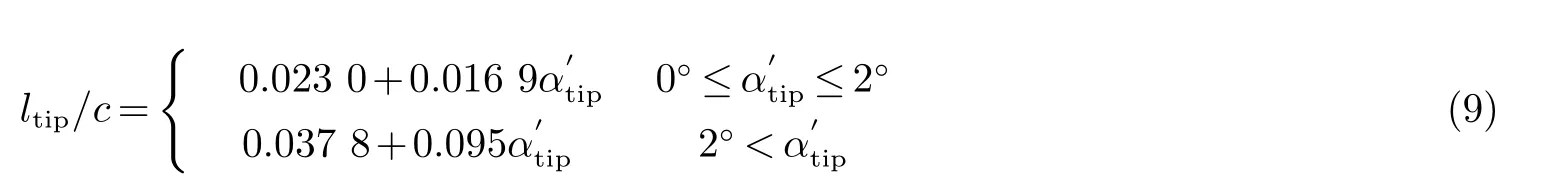
式中：αtip为叶尖几何攻角，为修正后的叶尖几何攻角，该修正基于叶尖载荷特性（主要参照理想条件下大展长、无弯扭、定常流）.

式中：L′为在展向位置y处单位展长对应的升力.

斯特劳哈尔数

式中：f为1/3倍频程频带；Mmax为叶尖尾缘失速区域流体最大速度；M为来流在叶尖区域的速度.

2 翼型尾缘厚度对DU21、DU30翼型的影响

为了研究尾缘厚度对翼型气动特性及噪声的影响，对两种DU翼型的尾缘厚度进行对称加厚变换[17].该方法不改变原始翼型最大厚度和中弧线分布，在最大厚度之后对称地增加翼型尾缘厚度，所增加的厚度以幂函数表达，以保证变换后翼型的外形连续且光滑，表达式如下：

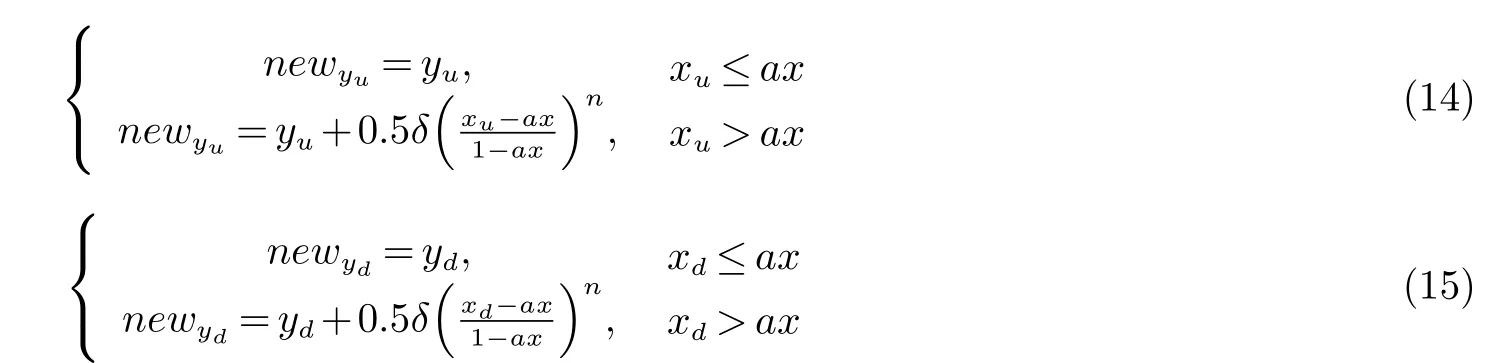
式中：xu为上翼面横坐标；yu为上翼面纵坐标；xd为翼面横坐标；yd为翼面纵坐标；ax为翼型最大相对厚度位置处横坐标；δ为尾缘厚度增加值；n为指数因子，一般选取范围n=1.5～2.5[18]，本文取n=2；newyu为上翼面纵坐标；newyd为下翼面纵坐标.

本文以DU93-W-210、DU97-W-300（下面简称DU21、DU30）为基础，采用上述方法进行钝尾缘设计.采用XFOIL软件计算翼型的气动特性，分析对比尾缘厚度的影响规律，默认雷诺数为2×106，马赫数为0.15，攻角范围为−5◦到20◦.采用扬州大学开发的风力机翼型噪声源仿真软件计算翼型气动噪声，该软件基于BPM半经验模型进行了部分修正，研究不同尾缘厚度对翼型气动噪声的影响规律，同时基于Howe工程模型研究锯齿尾缘降噪效果.若不做特殊说明，软件中参数均为默认值：来流合成风速80 m/s，接收距离1 m，接收角度90◦，翼型展长1 m，翼型弦长C=1 m，入流攻角5◦，钝尾缘厚度为弦长的0.1%，尾缘夹角20◦，翼型表面光滑，锯齿角度−2.5◦，锯齿的长和宽分别为0.15 m和0.25 m，声速为340 m/s，粘性系数为0.000 015 Pa·S.

2.1 不同尾缘厚度DU21翼型气动性能对比

在相同工况下，对比不同尾缘厚度的DU21翼型的气动性能，计算工况选取自由转捩工况.对DU21翼型进行尾缘对称加厚，厚度分别为：0.005C，0.01C，0.015C，0.02C，尾缘厚度增厚翼型表示为DUxx_xxx（如21%相对厚度DU翼型尾缘增厚0.005C表示为DU21_005）.DU21翼型及尾缘增厚翼型的型线局部对比如图6所示，由尖到钝依次为DU21原始翼型、DU21005、DU21_010、DU21_015、DU21_020翼型，各翼型的升力、阻力系数和升阻比的对比分别如图7、图8和图9所示.

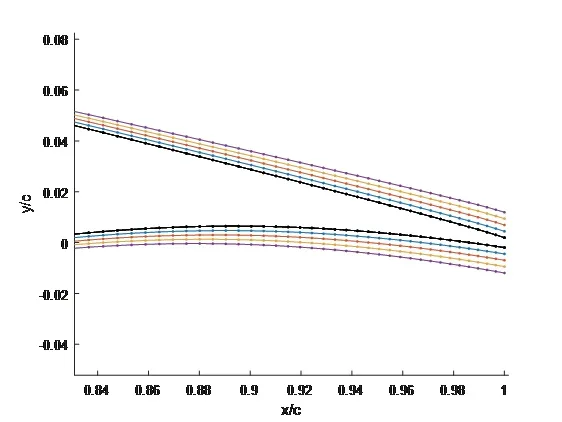
图6 不同尾缘厚度DU21翼型Fig 6 DU21 airfoil with different trailing edge thickness

由图7可知，对于不同的翼型，攻角较小时，尾缘增厚翼型的升力系数与原始翼型相差不大，攻角较大时，钝尾缘翼型的升力系数随尾缘变厚而增加，且均大于原始翼型.由图8可知，对于不同的翼型，攻角小于11◦时，各翼型的阻力系数较为接近，攻角大于11◦时，各翼型的阻力系数随着尾缘变厚而增大，且均大于原始翼型.在大攻角处，不同翼型在尾缘厚度递增的情况下，其阻力系数的变化趋势基本相同.攻角在5◦至10◦之间时，尾缘厚度的增加对DU21翼型阻力系数的影响最明显.由图9可知，攻角小于1◦或大于15◦时，尾缘增厚翼型的升阻比与原始翼型相差不大，攻角在1◦到15◦之间时，翼型的升阻比随尾缘厚度的增加而减小，但变化趋势不明显.因此，从功率产出角度考量，在设计制造拥有较薄翼型的叶尖区域时（叶片的主要功率产生区），应该严格控制尾缘厚度的加工误差.

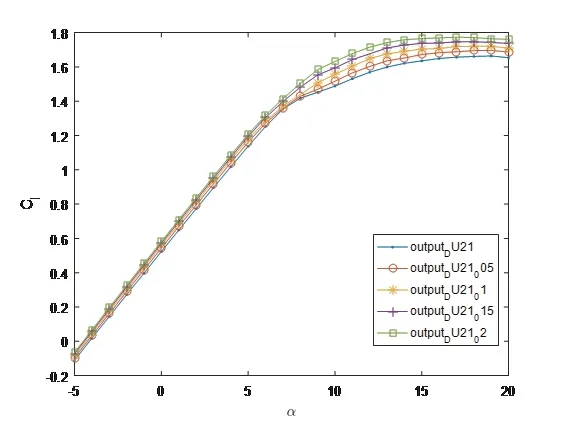
图7 不同尾缘厚度DU21翼型的升力曲线对比Fig 7 Comparison of lift coefficient curves of DU21 airfoil with different trailing edge thickness

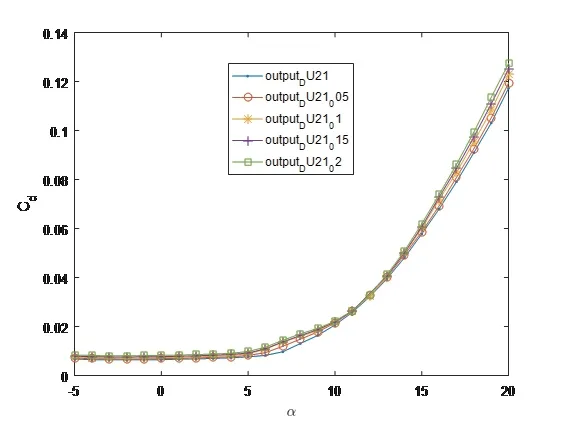
图8 不同尾缘厚度DU21翼型的阻力曲线对比Fig 8 Comparison of drag coefficient curves of DU21 airfoil with different trailing edge thickness

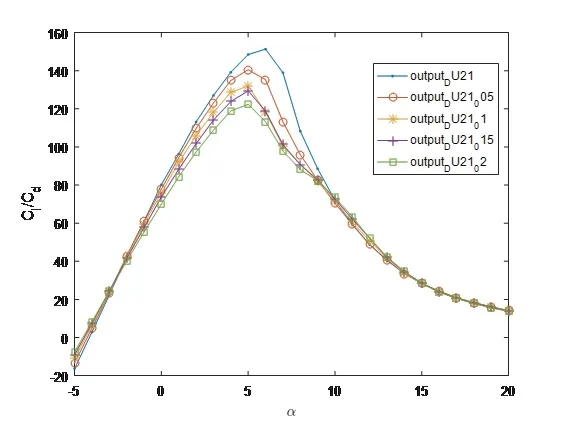
图9 不同尾缘厚度DU21翼型的升阻比曲线对比Fig 9 Comparison of lift to drag ratio curves of DU21 airfoil with different trailing edge thickness

2.2 不同尾缘厚度DU30翼型气动性能对比

在DU21相同的工况下，对比不同尾缘厚度的DU30翼型的气动性能.DU30翼型及尾缘增厚翼型的型线局部对比如图10所示，由尖到钝依次为DU30原始翼型、DU30_005、DU30_010、DU30_015、DU30_020翼型，各翼型的升力、阻力系数和升阻比的对比分别如图11、图12和图13所示.

图10 不同尾缘厚度DU30翼型Fig 10 DU30 airfoil with different trailing edge thickness

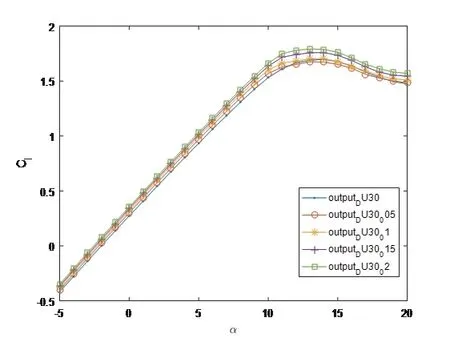
图11 不同尾缘厚度DU30翼型的升力曲线对比Fig 11 Comparison of lift coefficient curves of DU30 airfoil with different trailing edge thickness

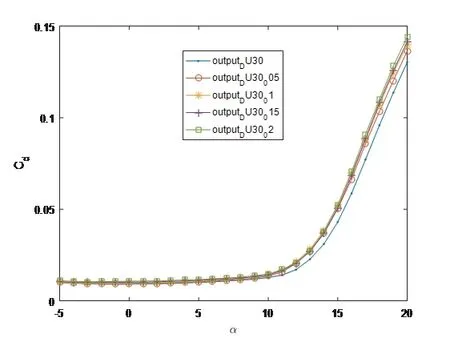
图12 不同尾缘厚度DU30翼型的阻力曲线对比Fig 12 Comparison of drag coefficient curves of DU30 airfoil with different trailing edge thickness

图13 不同尾缘厚度DU30翼型的升阻比曲线对比Fig 13 Comparison of lift to drag ratio curves of DU30 airfoil with different trailing edge thickness

由图11可知，DU30翼型升力系数随尾缘厚度的变化与DU21翼型相同，对于DU30翼型来说，尾缘厚度越大，升力系数的递增趋势越明显，这与文献[10]结果一致.由图12可知，DU30翼型阻力系数随尾缘厚度的变化与DF21翼型相同，攻角在5◦至10◦之间时，尾缘厚度的增加对DU30翼型影响更小.由图13可知，DU30翼型升阻比随尾缘厚度的变化与DF21翼型相同，对于厚度更大的DU30翼型，升阻比随尾缘厚度的变化更小，这与DU21和DU30翼型的阻力系数在攻角为5◦至10◦之间的变化规律相符.因此，从功率产出角度考量，对于拥有较厚翼型的近叶根区域，尾缘厚度的加工误差可以适当放宽，甚至可以主动增加尾缘厚度，使得叶片在升阻比损失不大的情况下，获得较大的结构性能提升.

2.3 不同尾缘厚度DU21DU30翼型气动噪声对比

在相同工况下，对比计算不同尾缘厚度的DU21、DU30翼型的气动噪声，翼型尾缘对称加厚的方法见图6和图10，同时研究锯齿尾缘翼型的降噪效果，与原始翼型对比，研究翼型气动噪声变化规律.由于人耳对不同频率的敏感性不同，为了反映人耳实际感受到的声音大小，引入了A、B和C加权声级.其中，最常用的是A加权法.A加权声级的测量单位为dB(A)，以下的声压级图谱中都做了A加权算法，表1和表2分别为DU21、DU30翼型在不同尾缘厚度下的噪声等级，图14表示原始DU21、DU30翼型声压级分布，图15和图16分别表示不同尾缘加厚的DU21、DU30翼型声压级分布.

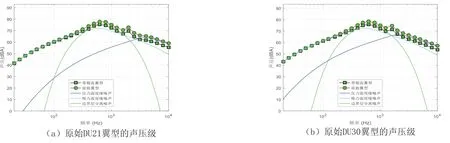
图14 原始DU21、DU30翼型的声压级Fig 14 Sound pressure level of original DU21 and DU30 airfoils

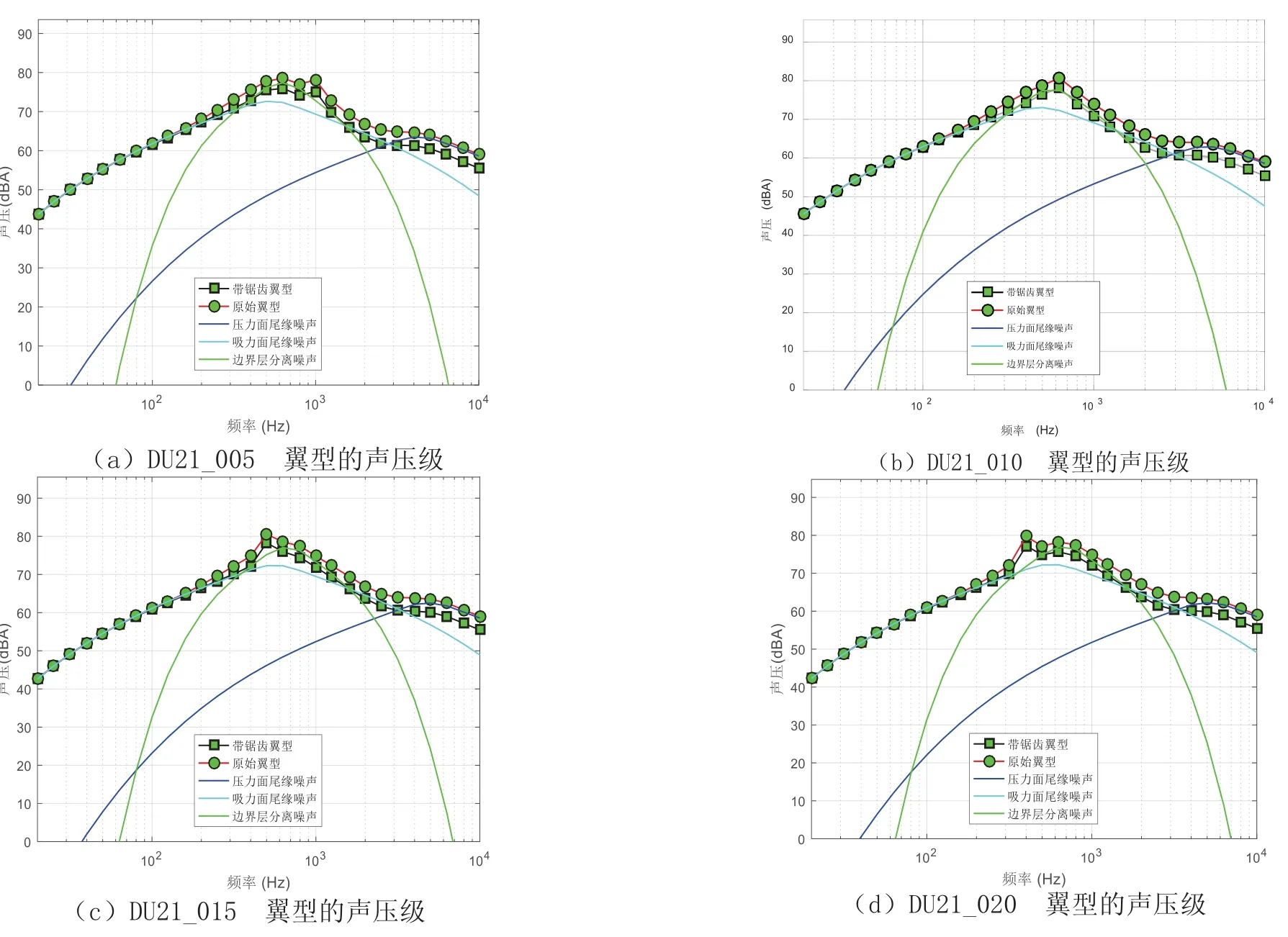
图15 不同尾缘厚度DU21翼型的声压级Fig 15 Sound pressure level of DU21 airfoil with different trailing edge thickness

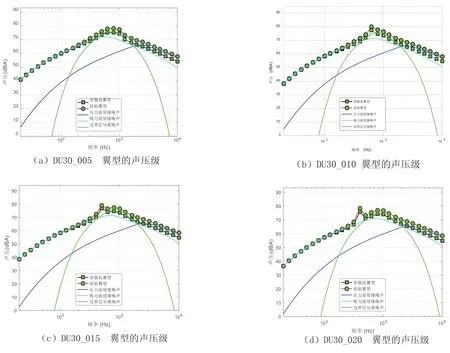
图16 不同尾缘厚度DU30翼型的声压级Fig 16 Sound pressure level of DU30 airfoil with different trailing edge thickness

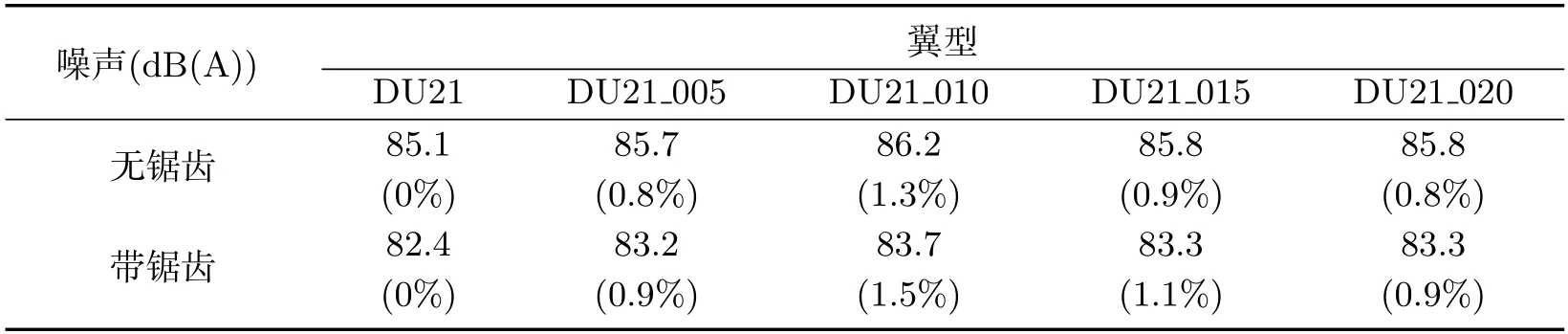
表1 不同尾缘厚度下DU21翼型的声压级Tab 1 Sound pressure level of DU21 airfoil with different trailing edge thickness

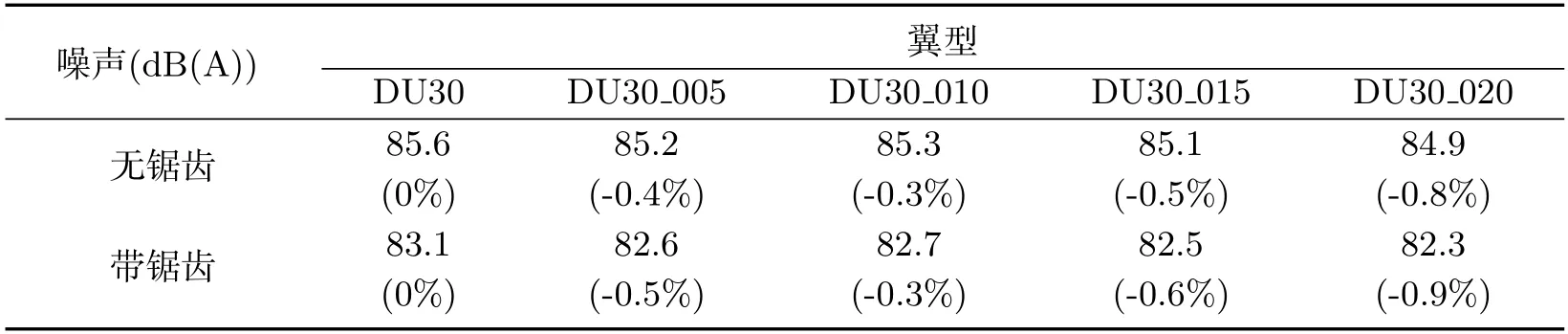
表2 不同尾缘厚度下DU30翼型的声压级Tab 2 Sound pressure level of DU30 airfoil with different trailing edge thickness

由图14～图16可知，尾缘厚度的变化会影响钝尾缘脱落噪声在总辐射噪声中的比例.当尾缘厚度增大到一定值时，总辐射噪声的变化尤为明显.对于不同的翼型，尾缘厚度的变化均主要影响200 Hz到2 000 Hz频率的声压级.尾缘厚度依次增加，其原始翼型和带锯齿翼型的最大声压级从较高频率到较低频率依次变化.由表1和表2可知，DU21翼型尾缘增厚时，其声压级呈现出明显的先增加后减小趋势，原始DU21翼型拥有最低的声压级.对于更厚的DU30翼型，其声压级在尾缘厚度较小时变化规律不明显；但在尾缘厚度大于0.01C 时，声压级随尾缘厚度增加而减小，且均小于原始DU30翼型声压级.上述尾缘增厚但声压级降低的情况，可能是尾缘增厚引起了气流分离滞缓，进而引起了噪声的降低.翼型加装锯齿后的声压级也呈现同一趋势，且均小于对应尾缘厚度的原始翼型.因此，从气动噪声角度考虑，在设计制造叶尖区域时，应该严格控制尾缘厚度的加工误差；而对于叶根区域，尾缘厚度误差精度可放宽.甚至可以适当增加尾缘厚度，在提高结构性能的同时，获得较小的噪声水平.

3 结论

本文以风力机专用翼型DU 93-W-210和DU 97-W-300为研究对象，探索尾缘厚度与气动噪声的关系，分别采用XFOIL软件和BPM半经验模型分析翼型的气动性能和气动噪声特性，得出以下结论：

（1）升阻比随尾缘厚度的增加而降低，尾缘增厚对较大厚度的DU 97-W-300翼型升阻比的影响较小，对较薄的DU 93-W-210翼型升阻比影响明显.

（2）气动噪声并不是随着尾缘钝度的增加而单调递增，在某个尾缘厚度范围内，气动噪声先增加后降低.对较大厚度的DU 97-W-300翼型，随着尾缘厚度的增大，声压级变化幅度较大；对于较小厚度的DU 93-W-210，声压级变化幅度较小，带锯齿的翼型声压级呈现同一趋势.

（3）在设计制造拥有较薄翼型的叶尖区域时，应该严格控制尾缘厚度的加工误差.对于拥有较厚翼型的近叶根区域，尾缘厚度的加工误差可以适当放宽，必要时可以主动增加尾缘厚度，在确保较低的气动噪声水平前提下，提升叶片结构性能.