基于模糊核均值聚类优化的光流测速方法

闫宝龙，赵东花，刘晓杰，吴新冬，闫德利，王晨光，申 冲

(1. 中北大学仪器科学与动态测试教育部重点实验室，太原 030051；2. 中北大学仪器与电子学院，太原 030051；3.中北大学信息与通信工程学院，太原 030051)

0 引言

全球定位系统(Global Positioning System，GPS)易受信号干扰[1]，惯性导航系统(Inertial Navigation System，INS)不仅成本高，而且单独工作时误差易随时间积累。近年来，随着成本低、自主性强的视觉导航技术发展[2-3]，光流法可被用于进行物体运动估计与目标跟踪，是视觉导航的一个重要研究方向。

自B.Horn等[4]在1981年提出光流算法基本原理后，引起国内外学者的广泛关注。光流即昆虫在飞行时观察物体，物体在其视网膜上形成一系列变化的图像信息，这些连续变化的图像信息不断“流过”视网膜(即图像平面)就形成了光流[5]。光流可以看作是观察3D运动的2D投影[6-10]。研究人员受此启发，将光流引入到无人机导航中[11]，由于无人机飞行时图像背景会发生变化，因此可利用所携带相机计算出在图像坐标系下的运动速度，然后通过图像中像素点与物体的投影关系，最终解算出无人机在地理坐标系下的速度信息。Amizai等[12]提出了一种金字塔分层光流算法，该方法能够在大位移形变时抑制光流估计误差，并相应研发了具有体积小、功耗低、成本低等优点的可应用于无人机的仿生光流导航系统。由于无人机的运动估计是由背景变化引起全局运动与场景中前景变化引起局部运动的组合，若采用光流法进行运动估计时不剔除由前景运动物体带来的局部运动中的光流干扰值和野值，将会导致光流测速精度降低。文献[13]为了提高光流测速精度，提出了一种梯度阈值法对噪声点进行处理，但是阈值大小无法确定，并且需根据无人机飞行场景变化实时调整阈值大小，这在实际导航中会带来不便。文献[14]针对前景与背景进行分割以消除前景影响，提出了一种模糊分类方法，但该方法对每张图像进行分割，计算量较大。

本文为了进一步提高载体运动速度的解算精度，提出了一种基于模糊核均值聚类算法优化的金字塔Lucas-Kanade光流测速方法(FKCM-金字塔LK)。该方法不仅收敛速度快，而且能处理大数据集，因此能够在大范围内减小由于图片信息丢失造成的计算不准确，同时还能将光流干扰值以及光流野值剔除，最终提高光流测速精度。

1 光流测速原理

光流法是利用三维空间运动物体的图像序列中像素在时间域上的变化以及相邻帧之间的相关性,找到上一帧与当前帧之间存在的对应关系，得到其在二维平面上的运动。如图1所示，图像中的每一个点都对应一个空间点，每一个空间点相对于摄像机的速度向量都可以投影为像平面上一个点上的二维速度向量，而每个像素的二维速度向量就构成了运动场。该方法需要3个前提条件：

1)相邻图像间时间连续，且物体做微小运动；

2)保持空间一致性；

3)相邻图像之间的亮度保持不变。

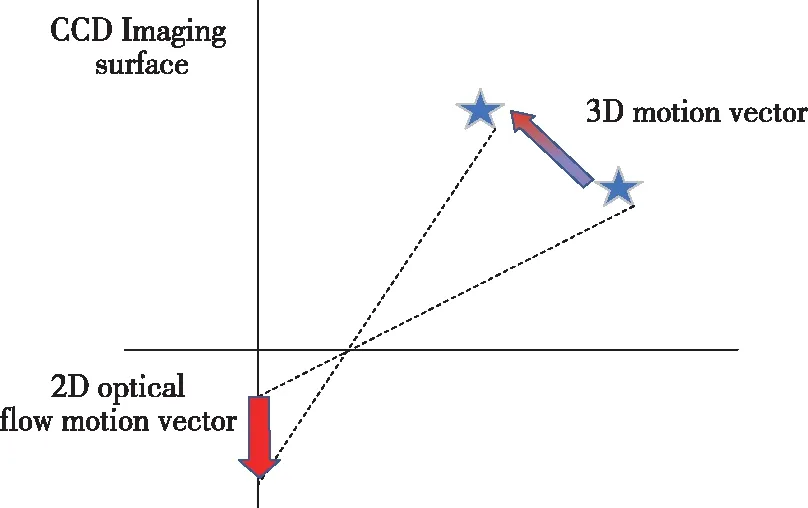
图1 运动场与光流场对应关系图Fig.1 Corresponding diagram of motion field and optical flow field

假设图像中一点(x,y)在t时刻的亮度为I(x,y)，同时，假设该点在垂直方向上的分量表示为μ(x,y)，在水平方向上的分量表示为v(x,y)，则可以得到

(1)

在经过一段时间间隔Δt后，该光流点的亮度为I(x+Δt,y+Δt,t+Δt)，当Δt趋近于0时，可以假设该点亮度不变，得到

I(x,y,t)=I(x+Δt,y+Δt,t+Δt)

(2)

当该点亮度发生变化时，则移动后该点亮度可以用Taylor公式进行展开计算，得到

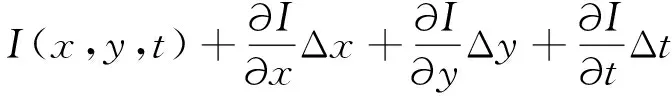
(3)

当式(3)中的二阶无穷小接近于0，且Δt趋近于0时，则有

(4)

式中，ω=(μ,v)，令

(5)

Ixμ+Iyv+Izt=0

(6)

由上述计算可知，传统LK算法需要满足3个约束条件，而无人机导航过程大幅运动时很难保持所需的3个约束条件，因此易出现计算的特征点误差大的问题。金字塔LK算法可在此基础上将图像分层计算并缩小图像尺寸，使用小尺寸上的像素点代表更大尺寸图像上的多个像素点[15]。

金字塔LK算法首先利用低通滤波平滑曲线对图像进行采样，生成金字塔图像，每一层图像的高度与宽度是下一层的一半；然后从最顶层计算图像的光流，利用最顶层光流的计算结果估计下一层光流的初始值进行金字塔跟踪；最后将上层图像得到的光流矢量叠加作为下一层的初始值进行迭代，最终计算得到的光流值就是所有层光流矢量的叠加(见图2)。这样就可以利用相对较小的领域窗口处理更大尺寸图像上的像素移动[16]。其具体实现过程如下：

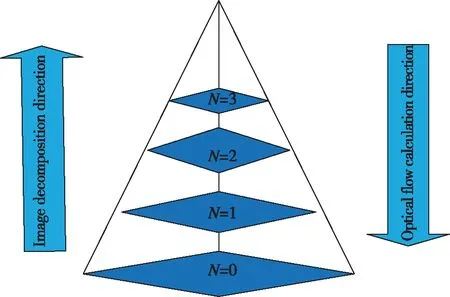
图2 图像金字塔Fig.2 The image pyramid

设相邻的两帧图像分别为M1和M2,在一个大小为o的窗口邻域中，假设ε是前后两帧图像的光流残差，则

(7)

光流计算方向与图像分解方向相反，首先在第n层进行光流估计，计算的结果反馈到n-1层，并作为n-1层的初始值，这样逐层传递，直到第0层为止。则式(7)变成

ε=εn(dμ,dv)

(8)

其中，每层光流估计值通过式(9)传递给下一层，并作为下一层的初始值

gn-1=2(gn+dn)

(9)

通常，最顶层的初始值为0，即gn=(0,0)。因此，金字塔LK算法通过对图像尺寸的缩小,使得小像素点可以涵盖更多像素点信息,从而更容易实现传统LK算法的约束条件，最终降低所计算特征点的误差。

2 基于模糊核均值聚类的金字塔LK光流算法

由于前景运动物体所形成的光流值的大小通常与背景光流相异，从数据处理角度应将干扰项剔除。但由于缺少干扰项的速度先验信息，光流测速中常用于改善精度的随机抽样一致(Random Sample Consensus，RANSAC)算法[16]与基于前后向误差的归一化互相关匹配值(Normalization Cross Correlation，NCC)算法[17]在有效排除干扰项的能力上还有待提升。利用聚类算法将光流值按照光流数据分布的概率峰值进行聚类，可以将背景光流与干扰项进行区分，从而将干扰项剔除[18]。其中，Mean-Shift聚类算法需要选定聚类初始值，K-means聚类算法需要对初始聚类中心进行选择。而模糊核均值聚类只需要确定聚类数以及终止误差即可进行求解，具有较快的解算速度，因此在本文中将模糊核均值聚类算法与金字塔LK算法相结合。其中，模糊核均值聚类算法是将隶属度的概念引入到聚类算法中，首先通过优化目标函数，以获得每个样本中的数据对于所有聚类中心的隶属度，判断样本数据的归属以便对数据进行自动分类[19]。然后，计算出光流值以及载体在相机坐标系下的速度，最后经过坐标系转换，就可以得到地理坐标系下的速度。

本文提出的基于模糊核均值聚类金字塔LK光流算法的具体过程如下：

1)通过模糊核均值聚类算法将样本数据非线性映射Φ映射到高维特征空间[20]，在高维特征空间中得到映射集为Φ(xk)(k=1,2,…，N)，由米氏(Mercer)定理可知，输入空间中样本空间的内积在隐射空间通过K(xi,xj)=[Φ(xi),Φ(xj)]求得。如果样本的聚类数为C，第i类的聚类中心为pi，在此i类中第k个样本的隶属度为uik∈[0,1]，则模糊核聚类算法的目标函数为

(10)

(11)

d2(xk,pi)=K(xk,xk)-2K(xk,pi)+

K(pi,pi)

(12)

在模糊聚类中引入核函数，是因为通过核运算可以得到新的距离度量，从而产生了同一空间不同距离的聚类[21]。

2)将金字塔LK光流算法利用模糊核均值聚类算法进行分组，选取包含像素速度最多的一组，取其平均值作为最终的光流值。假设像素相邻区域空间运动的矢量一致，计算相邻图像中对应像素点流向信息，获取特征点附近小窗口局部信息以及匹配光流矢量。使用超定方程组对式(6)进行求解，得到中心点的运动参数[22]，其方程可表示为

(13)

使用最小二乘法可以求出μ、v两向量的大小

(14)

(15)

利用μ、v矢量大小即可求得实际运动速度。

3 实验验证

3.1 仿真实验

本次仿真实验首先在Google Earth上采集图像，再使用Matlab中imcrop函数固定裁剪框的大小，得到两个大小相同的图片，在使用该函数过程中，设置移动的像素值作为基准值，移动距离通过Google Earth的“标尺”功能在图片上标明。一组仿真实验为无人机速度为12m/s，在对地高度120m的位置进行拍摄，光流图像矢量图如图3所示。在Matlab中设置横向位移像素值为15像素，使用金字塔LK算法的求解结果为移动13.9548像素，误差为6.96%。通过FKCM-金字塔LK算法的求解结果为移动14.6310像素,误差为2.46%。

(a) 金字塔LK解算运动方向

由仿真实验可以看出(见图4)，通过基于模糊核均值聚类算法优化的金字塔LK算法与传统金字塔LK算法相比，无论在高地环境还是城市环境中，金字塔LK解算运动矢量的方向与真实方向大致一致，但是存在干扰项，经过聚类算法优化后，可将干扰项剔除。同时，经过优化后的金字塔LK算法解算移动的像素值更加靠近真实值，并且有效减小了干扰项与光流信息丢失导致的光流值误差，使得载体速度解算精度更高。

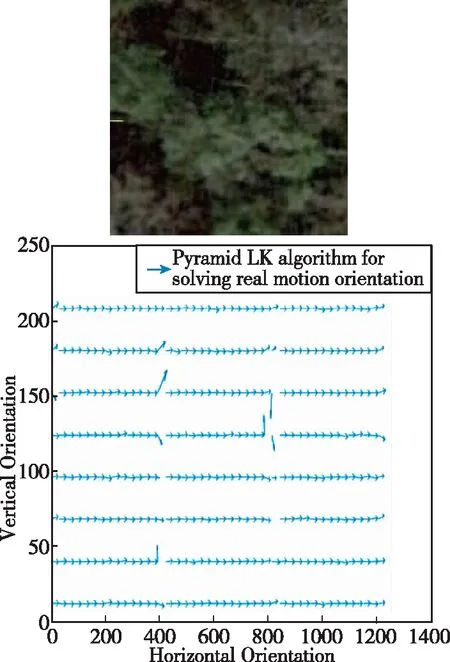
(a) 金字塔LK解算运动方向

3.2 室外实验

利用无人机进行室外实验，实验设备如图5所示，实验设备参数如表1所示。实验过程中，无人机在对地30m高度飞行，同时控制无人机飞行速度为2.3m/s，无人机沿正东方向飞行，X方向前进约50m，Y方向基本保持恒定。采集并截取无人机运动过程中的视频图像，使用金字塔LK算法、Horn-Schunck算法、本文提出的FKCM-金字塔LK算法分别进行对比处理，实验结果如图6及表2所示。

图5 室外实验图Fig.5 Outdoor experiment

表1 摄像头参数表

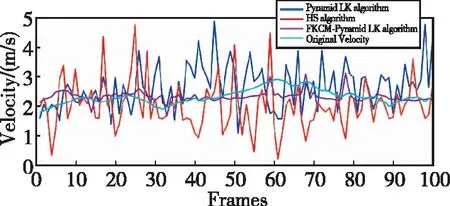
图6 光流算法速度对比曲线Fig.6 Comparison curve of optical flow velocity by different algorithms

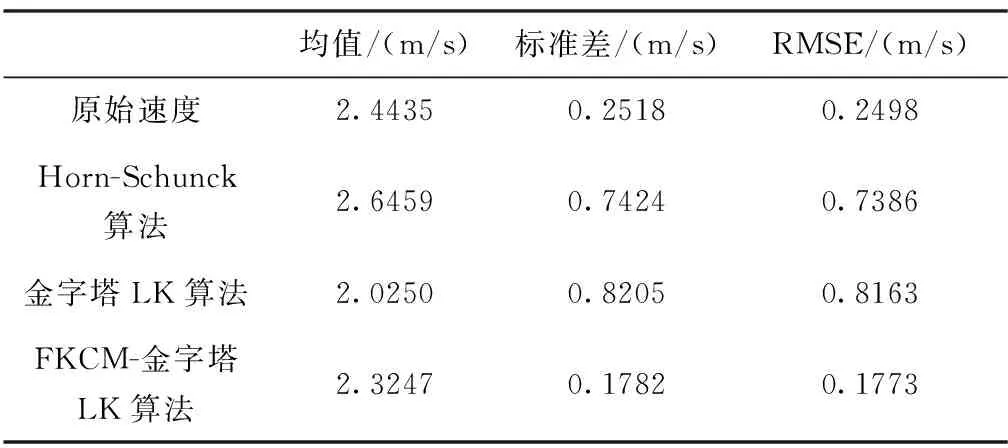
表2 HS算法、金字塔LK算法与FKCM-金字塔LK算法对比

由上述分析可知，HS算法对实际运动过程中解算的速度后半区域出现解算错误，金字塔LK算法对实际运动过程中的测速结果波动性较大，而使用本文提出的FKCM-金字塔LK算法解算速度值更加平滑和稳定，最终更加靠近真实值。利用该方法解算的速度标准差由0.8205m/s降低到0.1782m/s，精度提升79.28%;与此同时，使用该方法解算的RMSE由0.8163m/s降低到0.1773m/s,精度提升78.28%。光流测速的精度得到了有效提高。

4 结论与展望

本文针对视觉导航中光流信息容易受到物体相对运动影响的问题，提出了一种基于模糊核均值聚类算法优化的金字塔LK光流测速方法。该方法不仅可以有效地减少物体相对移动对光流测速的影响，而且可以使得光流测速精度大幅提高。本文结合目前现有的研究成果，对未来优化光流算法技术面临的挑战进行展望。

1)实验过程中，无人机由于受到气流的影响，飞行时会产生抖动，导致光流解算的速度偏离基准值，可以使用增稳系统或者去抖动算法进行改进，使得计算出来的速度更接近准确值。

2)虽然光流算法在速度测量精度方面得到了一定提升，但其应用依然受光流法假设的影响，因此可以对光流算法做进一步改进，如采用强鲁棒图像特征点提取方法等。