基于联邦自适应滤波的分布式传递对准方法

朱 敏，马 振，王俊玮，陈熙源

(东南大学仪器科学与工程学院， 南京 210096)

0 引言

分布式位姿测量系统可为高分辨率航空对地观测系统多元载荷提供分布式高精度运动信息。但观测平台在飞行过程中受到载荷和湍流的影响，机翼发生挠曲变形和震颤，降低了主子节点之间传递对准的精度[1-2]。因此，提高分布式传递对准的精度成为航空对地观测系统高分辨率成像的关键。

传统的不考虑主子节点动态变形的传递对准误差模型以及不考虑噪声的时变特性和主子节点间信息融合的分布式卡尔曼滤波算法用于分布式传递对准时难以提供高精度信息。传统传递对准误差模型将机翼视为刚体，忽略了主子节点之间的动态变形，难以实现高精度测量。文献[3-4]使用二阶Markov模拟动态弯曲变形角，并将相关弯曲变形角和角速率加入状态变量，但其模型中将动态杠杆臂视为常数，并不符合实际变形。文献[5]建立了变形角和动态杆臂之间的模型，对主子节点之间的速度关系进行包括耦合关系在内的详细分析。但在机载分布式传递对准过程中，机翼变形会增加杆臂的估计误差，姿态以及角速度匹配方法可避免该误差[6]。所以，主子节点之间角速度耦合关系，即机翼挠曲变形引起的角速度同子节点角速度方向不同而存在的耦合角也需要考虑。因此，在传递对准误差模型建立时考虑了机翼的挠曲变形角、耦合角、主子节点的动态杆臂误差。但在实际的工程应用中，尽管使用了较为精确的模型，复杂飞行环境的干扰仍会导致卡尔曼滤波精度下降，甚至滤波发散，自适应滤波方法成为研究重点[7-9]。文献[10]提出了基于新息极大似然估计准则的自适应卡尔曼滤波器,实时估计出系统过程噪声矩阵Q和量测噪声矩阵R，可以较好估计出失准角，但每一次均要进行Q和R的估计，大的计算量会导致实时性降低。因此，考虑到传递对准的精度和时间，采用只对R进行不断估计的方法，但状态估计误差会影响该滤波算法的稳定性。基于残差的卡方检验[11]可有效解决该问题。因此，本文引入R更新和基于卡方检验的协方差矩阵P更新的卡尔曼滤波算法进行单点传递对准。但单一的自适应卡尔曼滤波用于分布式传递对准时抗扰动性能较差，可将不同的子滤波器进行信息融合以达到更好的效果[12]。在多节点信息融合算法中，联邦滤波因其较好的容错性而被广泛应用，其通过实时确定信息权重系数的方式对联邦滤波器进行了改进[13-14]。因此，本文结合分布式传递对准的背景和复杂飞行环境，以提高传递对准的精度和稳定性、缩短传递对准的时间为目标，提出了新型联邦自适应滤波算法用于分布式传递对准，子滤波器采用基于R和P自适应更新的卡尔曼滤波(Adaptive Kalman Filter，AKF)并结合27维传递对准模型进行单点传递对准，主滤波器采用基于误差协方差矩阵的范数的原则对多个子滤波器进行信息融合。

1 新型联邦自适应滤波算法

1.1 分布式位姿测量系统

分布式位姿测量系统包括一个高精度的主IMU和多个子IMU，示意图如图1所示。由于飞机的机翼部分可承受质量有一定限制，所以机翼上安装的多个子IMU为低精度。各个子节点处高精度运动信息的获取需利用主IMU测得的高精度运动信息对分布于机翼的多个子IMU进行分布式传递对准滤波估计[15]。分布式传递对准精度取决于传递对准模型和分布式传递对准滤波方法。

图1 分布式位姿测量系统示意图Fig.1 Schematic diagram of distributed position and orientation system

本文采用27维状态量的传递对准模型，将机翼的挠曲变形角、耦合角、主子节点的动态杆臂误差均进行考虑，模型[16]如下：

状态方程中状态变量为

(1)

状态方程中状态转移矩阵为

(2)

量测方程中量测量包括主子节点之间的姿态差Ya、速度差Yv和角速度差Yω

(3)

量测方程中量测矩阵为

(4)

(5)

(6)

传递对准过程中不确定的模型以及时变的飞行环境噪声等会带来误差。不考虑噪声时变特性和主子节点信息融合的分布式卡尔曼滤波算法用于分布式传递对准时难以提供高精度信息。为了保证传递对准精度和稳定性，将新型联邦自适应滤波算法用于分布式传递对准。子滤波器中使用基于R和P自适应更新的卡尔曼滤波算法，主滤波器基于误差协方差矩阵进行信息融合。

1.2 自适应卡尔曼滤波算法

传递对准时系统模型会产生不可预知的变化，需不断地估计Q和R来提高精度，但其存在着计算量大和自适应性差的问题。每一次滤波均要进行Q和R的估计，计算量大，实时性降低，并且随着滤波递推次数的增加,分配权重不断减小，滤波自适应性降低[14]。为保证滤波精度和速度，采用基于R和P自适应更新的卡尔曼滤波算法。

针对实时性问题，在Sage-Husa自适应卡尔曼滤波的基础上选择只进行量测噪声R更新的卡尔曼滤波算法。传递对准中主惯导采用高精度的IMU，同时还有相应的辅助导航设备以修正主惯导误差，常认为主惯导输出信息的精度较高并且较稳定。但是由于在实际传递对准中，受机翼挠曲变形和振颤的影响，机体运动速度、姿态以及角速度会发生变化，且变化较为复杂，虽在传递对准误差建模中已针对机翼挠曲变形进行建模，但其并未完全消除机翼变形带来的影响。相对于量测噪声而言，系统过程噪声受子惯导惯性器件误差的影响较小。因此，为减少滤波器的计算量并增加其稳定性，本文采用只进行量测噪声R更新的卡尔曼滤波算法，将量测噪声R不断估计并传入，进行滤波增益的更新，从而达到更精确的状态估计，具体算法流程如图2所示。

图2 R更新的卡尔曼滤波算法Fig.2 Kalman filtering algorithm based on R-update

R更新方程中自适应系数dk和遗忘因子[14]关系如下

dk=(1-a)/(1-ak)

(7)

其中，遗忘因子a的取值范围为0.95～0.99。

针对滤波的自适应问题，上述只进行R更新的卡尔曼滤波算法，在R更新方程中递推次数到一定值后，自适应系数收敛为常数，历史和新近的观测信息对滤波的影响保持固定比例，历史观测信息对滤波影响较大，滤波的自适应性较差。所以，滤波过程中针对滤波递推次数进行相应调整，每次滤波结束后判断自适应是否为常数，若为常数，将滤波次数k从0开始计数，重新进行自适应调整，继续执行图2所示滤波过程。

然而，系统模型的不确定性会降低基于R自适应更新的卡尔曼滤波器的性能，只进行R更新的卡尔曼滤波算法易受到状态估计误差的影响，计算稳定性相对较差。为克服该问题，本文引入卡方检验以及自适应因子[17]。通过基于残差序列的卡方检验评估传递对准模型的滤波稳定性，并采用自适应因子动态调整状态估计误差的均方误差阵，具体如下：

通过卡方检验验证滤波器是否平稳，当检测到滤波不是最优时，P阵进行自适应更新，引入自适应因子调整状态协方差矩阵并考虑对称性，P的表达式更新为式(8)

(8)

其中，Sk为自适应因子。

当滤波最优时，残差序列rk有下列属性

(9)

其中，γk服从可观测状态变量的数量为m自由度的卡方分布。

式(9)中，令

(10)

(11)

(12)

根据式(9)可知，滤波最优时残差序列的每一个分量满足下列方程

γi(k)=[ri(k)]2/(aii(k)+bii(k))～χ(1)

(13)

其中，aii(k)为矩阵Ak的第i个对角线元素；bii(k) 为矩阵Bk第i个对角线元素。

对Ak进行分解可得到Ak和Jk的关系

(14)

其中，Jii(k)为矩阵Jk的第i个对角线元素。

结合式(13)和式(14)，自适应因子满足下列方程

(15)

其中，εi为卡方检验的阈值。

检测到滤波异常时，为使滤波正常，自适应因子公式如下

Si=

(16)

自适应因子矩阵中只有可观测状态量可以自适应计算，其余不可观测的值均取为1。因此，可观测状态量的自适应因子取值如式(16)，不可观测状态量取值为1。

自适应因子矩阵表达式如下

Sk=diag(s1,s2,s3,…,sn)

(17)

综上所述，基于R和P自适应更新的卡尔曼滤波算法整体流程如图3所示。

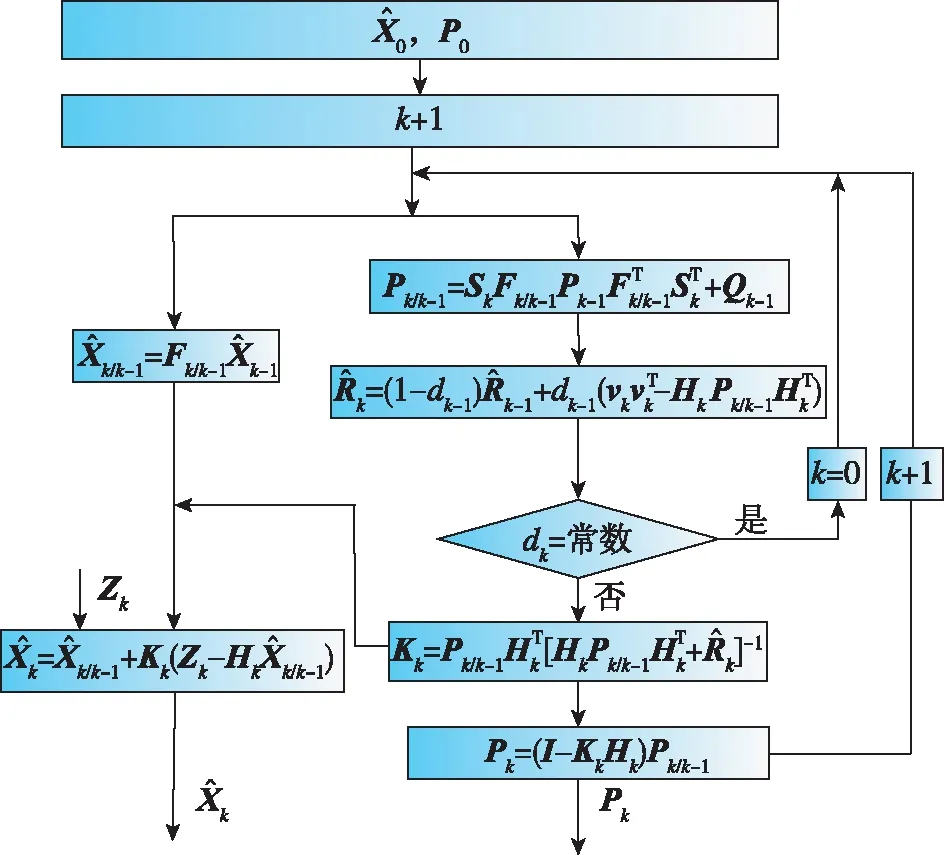
图3 自适应卡尔曼滤波算法Fig.3 Adaptive Kalman filtering algorithm

1.3 基于误差协方差矩阵的信息融合算法

为提高分布式传递对准精度和稳定性，采用基于误差协方差矩阵的信息融合算法。结合子滤波器中的自适应卡尔曼滤波算法，以3个子IMU为例的新型联邦自适应滤波算法的滤波结构如图4所示。

图4 新型联邦自适应滤波算法Fig.4 Novel federated adaptive filtering algorithm

子滤波器中分别进行基于R和P自适应更新的卡尔曼滤波算法的传递对准后，在主滤波器中通过信息融合进行全局最优估计，然后将计算出的协方差阵乘以信息分配因子系数,反馈给各个子滤波器进行权重的分配。信息分配因子αj为权重分配提供基准，其可通过误差协方差矩阵P的范数被确定。子滤波器的滤波效果表达式如下

(18)

其中，j=1,2,3代表滤波器的序号。

信息权重因子αj的表达式如下

(19)

信息融合原则为

(20)

信息权重分配原则为

(21)

2 实验结果及分析

2.1 半物理仿真实验

为了验证基于27维传递对准模型的新型联邦自适应滤波算法的有效性，本文采用基于实际飞行数据的半物理仿真方法，使用Y12型飞机进行约200min、6000m高的飞行实验，并记录飞行数据。其飞行轨迹如图5所示。

图5 飞行轨迹Fig.5 Flight trajectory

实验所使用的仿真数据基于上述实际飞行轨迹生成。其中主IMU数据采用本次飞行实验数据，3个子IMU数据将飞行实验中主IMU数据进行转换，再叠加设定的子 IMU的误差。参数设置如表1所示。

表1 子IMU参数设置

2.2 结果及分析

3个子IMU分别采用传统卡尔曼滤波算法、联邦自适应滤波算法、新型联邦自适应滤波算法三种算法进行分布式传递对准,以证明联邦自适应滤波算法以及自适应卡尔曼滤波算法的有效性，最终证明本文提出的新型联邦自适应滤波算法的有效性。三种滤波算法均采用27维传递对准模型，选用杆臂误差和姿态误差作为评估对象。传统卡尔曼滤波算法和联邦自适应滤波算法对比仿真实验结果如图6和图7所示。

图6 杆臂估计误差对比图Fig.6 Comparison of lever arm estimation error

图7 姿态估计误差对比图Fig.7 Comparison of attitude estimation error

传统卡尔曼滤波算法和新型联邦自适应滤波算法对比仿真实验结果如图8和图9所示。

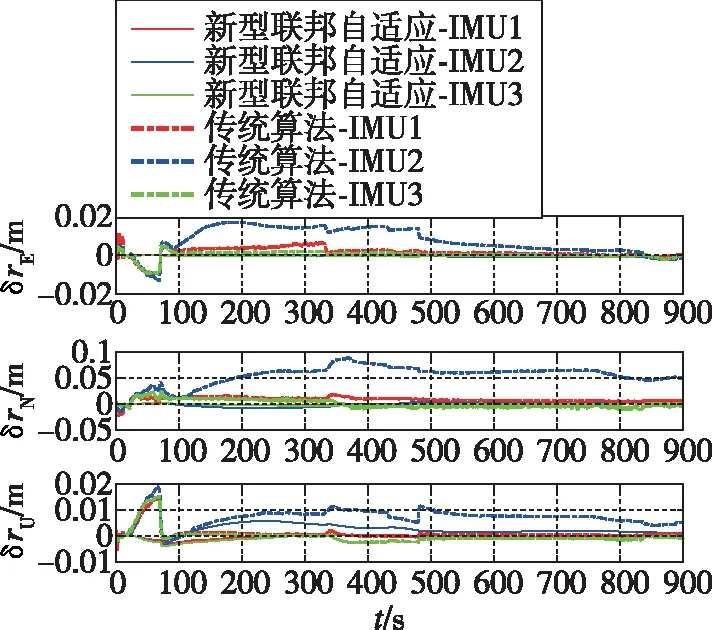
图8 杆臂估计误差对比图Fig.8 Comparison of lever arm estimation error

图9 姿态估计误差对比图Fig.9 Comparison of attitude estimation error

将图8、图9和图6、图7进行对比可以看出，相较于传统卡尔曼滤波算法以及子滤波器使用卡尔曼滤波的联邦自适应滤波算法，新型联邦自适应滤波算法可提高动态杆臂以及姿态估计的稳定性和精度。在卡尔曼滤波算法下，动态杆臂估计精度较差，姿态角估计稳定性较差，滤波器处于振荡效果，并且航向角的估计精度较差。因此，算法效果主要以稳定性和动态杆臂、航向角的估计精度为评判标准。由于飞行过程中机翼振动和挠曲变形会导致量测信息噪声时变，飞行环境的多变性则会导致受扰动较大。若使用传统卡尔曼滤波方法无法有效进行杆臂和姿态的校正，误差迅速增大，降低了传递对准的稳定性、快速性和精度。虽然使用联邦自适应滤波算法可提高杆臂和姿态的估计精度，增加整体的抗扰动性能，但子滤波器估计的信息振荡严重、收敛缓慢，且未考虑系统噪声和量测噪声的影响，传入主滤波器后降低了信息融合的效果。本文提出的新型联邦自适应滤波算法有效解决了上述问题。子滤波器中R自适应更新的加入，对时变噪声有一定调节能力，可以正确估计Rk，实时调整增益K，P自适应更新的加入，对系统噪声特性的影响进行削减，同时主滤波器进行信息融合，促进了整体滤波器的抗扰动性能，增强了校正效果。新型联邦自适应滤波算法缩短了传递对准的时间，提高了传递对准的精度，增强了传递对准的稳定性。

为直观分析提出方法的有效性，三种算法的动态杆臂及航向角估计的均方根误差(Root Mean Square Error，RMSE)计算如表2和表3所示。选用RMSE作为评估标准，相较于传统的卡尔曼滤波算法，新型联邦自适应滤波算法用于分布式传递对准时动态杆臂估计精度提高了61.54%，航向角估计精度提高了42.35%。

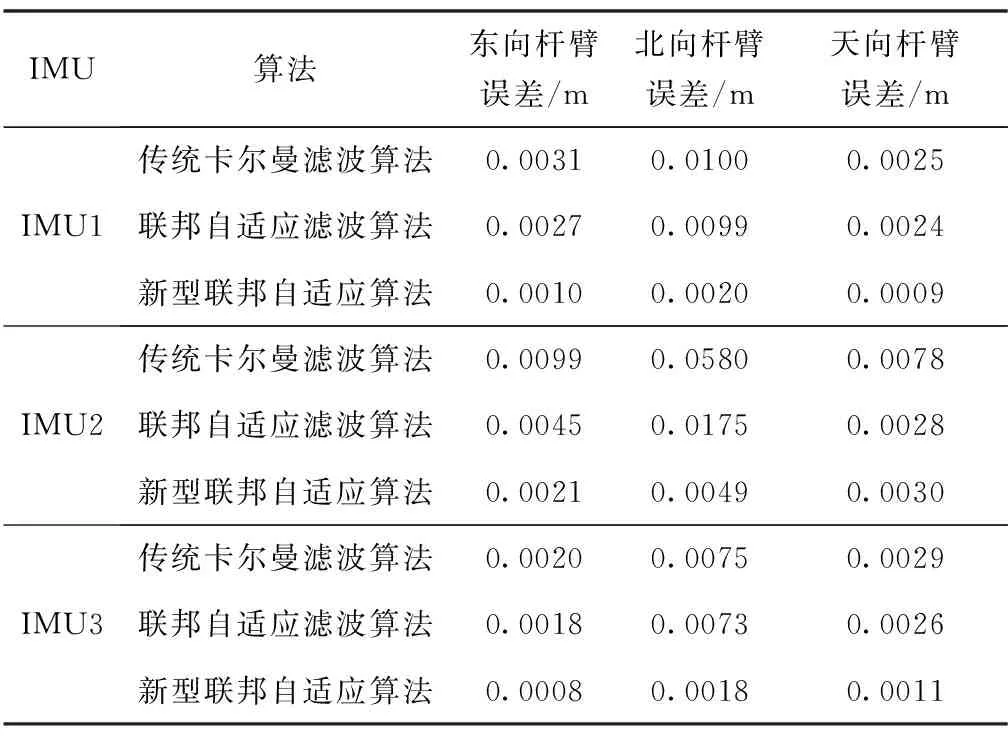
表2 杆臂估计误差结果对比

表3 航向角估计误差结果对比

3 结论

针对分布式传递对准精度下降和稳定性问题，提出了子滤波器采用基于R和P自适应更新的卡尔曼滤波算法并结合27维传递对准模型用于主子传递对准，然后对不同子滤波器采用基于误差协方差矩阵原则进行信息融合和权重分配。算法分析和实验结果表明：新型联邦自适应滤波算法中R自适应、P自适应以及信息融合方法的加入，抑制了量测信息噪声时变特性对子滤波器的影响，缓解了状态估计误差对滤波的影响，提高了抗扰动性能，动态杆臂和姿态估计稳定性和精度得到了提高，证明了新型联邦自适应滤波算法应用于分布式传递对准中的有效性。未来计划建立更精确的传递对准建模，将陀螺仪和加速度计进行更深层次的展开和分析以提高精度。