深挖折叠问题本源 发展核心素养潜能——以一道中考试题为例

昆明市第三中学 李加禄

折叠问题历年来都是中考的热点问题，具有知识覆盖面广、综合性强的特点，常常受到命题者的青睐，可以说是中考几何压轴题的常青树.笔者通过对2021年广东省中考数学第23题的多解探究，尝试用以题会类、触类旁通等方式，探寻解决此类问题的通性通法，以期达到“观一木而见森林”的效果，激发学生学习数学的兴趣，提升数学学科核心素养.

一、试题呈现

题目：（2021年广东省）如图1，边长为1的正方形ABCD中，点E为AD的中点.连接BE，将△ABE沿BE折叠得到△FBE，BF交于点G，求CG的长.

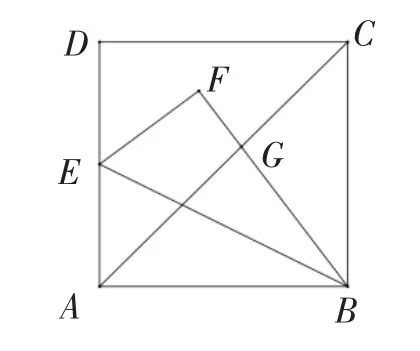
图1

二、试题解读

本题以正方形和三角形为背景，以折叠问题为载体，综合考查了初中阶段“数与代数”“图形与几何”的核心知识:正方形的几何性质、等腰直角三角形性质及轴对称的性质，如解方程（组）、一次函数、锐角三角函数、勾股定理、相似（全等）三角形和圆等.试题图形简洁、立意高妙、内涵丰富、梯度合适、解法多元，注重数学思想方法的应用，涉及方程思想、数形结合思想、化归思想等数学思想方法.可以说此题将基本知识、基本思想方法、基本技能进行了高度融合，凸显了逻辑推理、数学运算、直观想象和数学建模等核心素养.

三、思路探究

思路1：见平行，觅“X”型构相似.

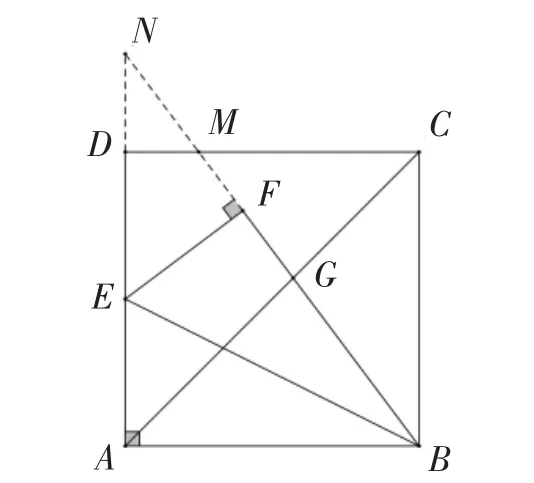
图2

由解法1可以看出，欲求CG的长需要找到与之相关联的结构（线段或三角形），于是我们考虑将CG放到已知的△BCG或△CGM中，以及线段AC上.因正方形对边平行，于是构造基本图形“X”型相似，延长AD交BF的延长线于点N，进而求出AN的长，再通过构建方程运用勾股定理求解，使问题迎刃而解.

思路2：见共边共角（或等角），觅“母子”型构相似.

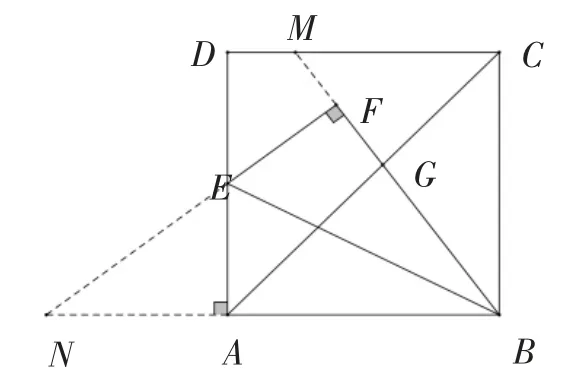
图3

考虑到题目中出现∠BFE=∠BAE=90°，于是将FE和BA延长相交于点N，构造常见的“母子”型相似，借助相似比为，设未知数进行转化，通过在Rt△ANE中构建勾股定理列方程求解.这种解法较好地考查了学生关联和重构基本知识的能力及数学建模的素养.

思路3：见直角，觅“一线三垂直”构“K”型相似.

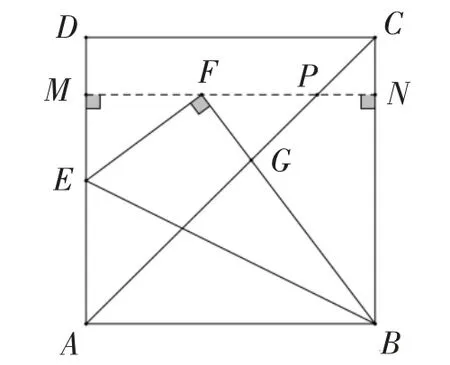
图4

当题目出现的特殊角是直角时，我们通常作两条垂线构造“一线三直角”全等或相似来解决问题.如解法3通过点F构造“一线三直角”，易证△EMF∽△FNB，可求得线段之间的数量关系，再利用勾股定理求出MF，进而求得最终解决问题.

思路4：见共点等线段，觅旋转变换构全等.

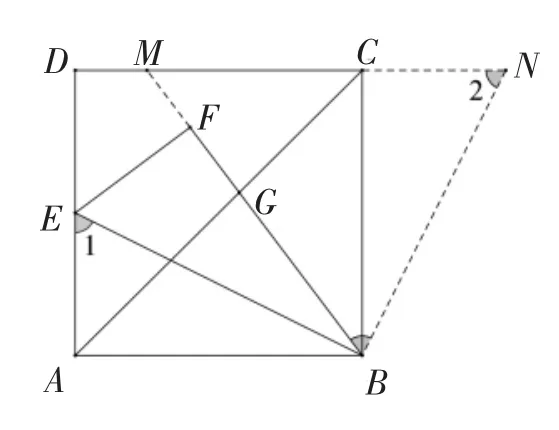
图5

当题干中有共端点等线段条件时，我们可以考虑旋转构造全等图形，特别是等腰三角形、等腰直角三角形、等边三角形、正方形内有一点时，可将思考的落脚点放在图形的旋转上.通过图形旋转变换，我们将题目中分散的条件集中在某个特殊图形中或实现边与角的转移，从而寻求解题思路.

思路5：见角平分线，觅平行构等腰三角形.

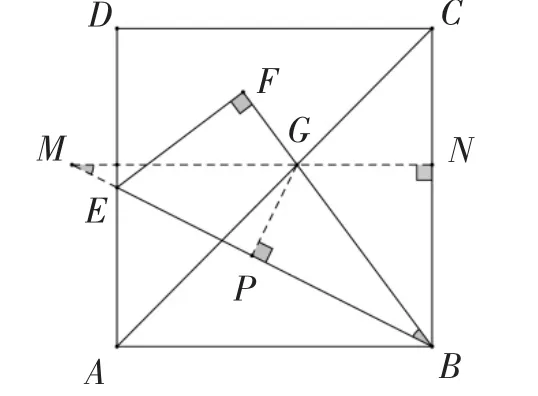
图6

解法5考虑到折叠问题有角平分线，于是我们可以尝试过角平分线上的点作某一边的平行线，构造等腰三角形，使分散的条件集中，让已知的边、角关系更具体化，解法自然生成.当然，只有学生对几何模型具有较强的洞察力和逻辑推理的素养，才能使问题得解.

思路6：以“数”解“形”，构建坐标系求解.

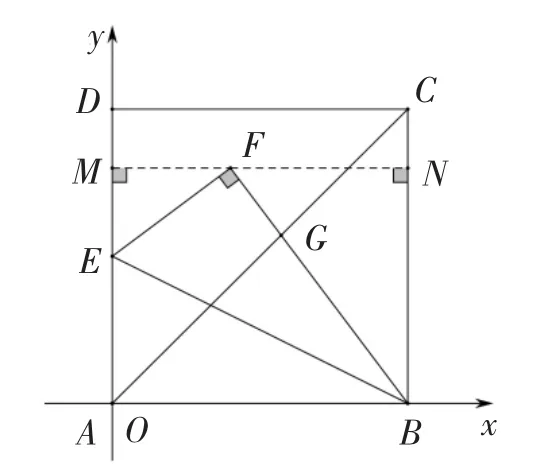
图7

如解法6，当题目图形满足某些特殊位置关系时，如本题中AB⊥AD，我们可利用几何图形的特殊性质建立平面直角坐标系，将几何问题代数化，图形性质坐标化，以“数”解“形”，以“形”助“数”，数形结合，用解析法求解，使解题思路更加直观简洁，优化了计算过程.

思路7：见直角，觅圆周角构辅助圆.

解法7:如图8，延长BF交CD于点M，作△BCM的外接⊙O，连接EM，EO，易知EO为梯形DABM的中位线，EO∥AB，于是EO⊥AD，则AD为⊙O的切线，点E在⊙O上，故∠MEB=90°，易证△EMF∽△BEF，则EF2=MF·BF，得.在Rt△BCM中下面解题过程同解法1，不再赘述.

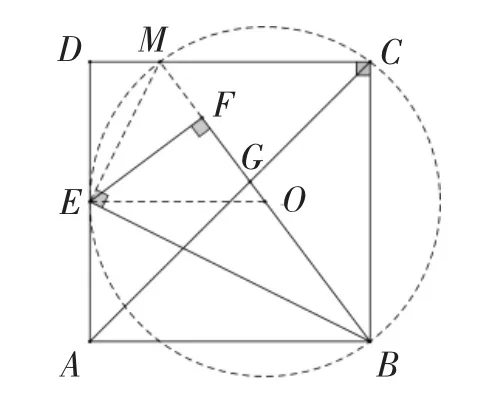
图8

对于对综合性、隐蔽性较强的平面几何问题，若我们能根据题目条件的本质特征，如解法7中∠BCM为直角，联想到圆的有关知识，恰当地构造辅助圆，利用圆的相关性质求解，往往可以化难为易，化隐为显，找到解题的新思路，使得求解之路变得“圆”来如此简单.诚然，这种解法要求学生具有较强的探索能力和敏锐的观察力，这里有无限风光在险峰之感.

思路8：利用二倍角正切函数求解.

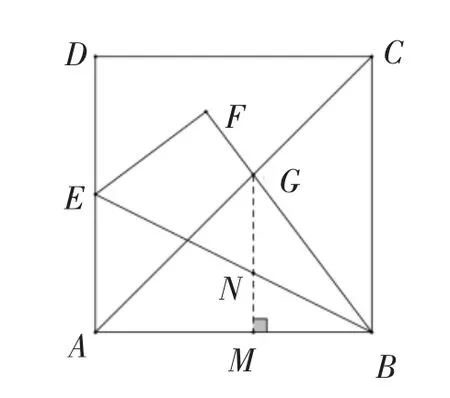
图9

解法8利用二倍角公式，直接体现三角形边、角之间的转化关系.虽然这种解法在初中阶段不作要求，但是对于学有余力的学生而言，可以作为一种方法的补充，有利于拓宽思维.

四、解题反思

1.关注核心条件，强化建模思想

本题的多样解法都可归功于“折叠问题”中的核心条件，从而展开丰富的联想，构造几何模型解题.正如美国著名数学教育家G·波利亚有过一个比喻:“一个好的数学问题和某种蘑菇有些相像，他们都是成堆地生长的，找到一个以后，你应该在周围找一找，很可能附近就有好几个.”本题中的解法1和2聚焦条件中的“翻折+平行”，联想构造“X”型和“母子”型相似模型求解；解法3和7聚焦于条件中的“∠BFE=90°”，联想构造“K”型相似和辅助圆模型求解；解法4聚焦于条件中的“正方形”，联想构造旋转变换，利用全等三角形求解；解法5聚焦于条件中的“角平分线”，联想构造等腰三角形求解；解法6聚焦于条件中的“轴对称”，联想构建直角坐标系求解.因此，日常教学中教师应强化学生数学建模意识，提炼数学模型，总结一些重要的基本模型，让其学会把陌生的、复杂的问题化归为熟悉的、简单的问题，提高学生的解题能力和学习兴趣，这也正是培养学生数学学科核心素养的关键所在.

2.关注通性通法，提升核心素养

章建跃博士指出:在“通性通法”中，“通性”就是概念所反映的数学基本性质，“通法”就是概念所蕴含的思想方法.注重基础知识及其蕴含的数学思想方法，才是追求数学教学的“长期利益”.如本题的8种解法都可归结为求线段CM长或tan∠CBF的值，找到了问题的通性，通法自然也就实现了.教师要引导学生从不同的角度挖掘题目条件，提升综合配置各种知识信息的能力，产生多种解题思路，尝试一题多解和多解归一，提炼通性通法，从而提高解题素养.正如德国教育家第斯多惠所说:“教学的艺术不在于传授本领，而在于激励、唤醒和鼓舞.”数学解题教学不应该是“授人以鱼”式的解题，而是教会学生探究解题本源的“渔趣”.教师只有不断深入挖掘题目里蕴含的数学思想和数学方法，尽可能地实现通性通法，提高学生的思维品质和创造性解决问题的能力，才能提升学生的数学素养.