考虑界面滑移效应的波形钢腹板箱梁解析解

许 晶，郑智仁,2，孔华辉，何桂峰

(1. 中国农业大学水利与土木工程学院，北京 100083； 2. 保利(甘肃)实业投资股份有限公司，甘肃兰州 730070)

0 引 言

波形钢腹板[1]组合箱梁采用波形钢腹板代替传统混凝土腹板，降低了结构自重，提高力学性能，并有效避免了腹板开裂问题。近年来，为克服混凝土底板支模、浇筑困难等[2]问题，提出了改进型波形钢腹板组合箱梁。该结构使用钢下翼缘板，相较于传统的混凝土下翼缘板，改进型可以有效降低下翼板厚度，提升组合箱梁整体性和跨越性，提高施工效率[3]。

箱梁在挠曲变形时，由于翼缘板平面内剪切变形影响，使其纵向弯曲正应力分布不均，产生剪滞效应[4]。国内外学者对组合箱梁剪滞效应进行了大量研究[5-11]。Reissner[6]最早提出利用能量变分法求解剪滞后问题，并构造了合理的剪滞后翘曲纵向位移差函数格式；聂建国等[7-8]建立了考虑剪滞后效应的钢-混凝土组合梁理论模型，并结合有效刚度法给出了组合梁挠度计算的简便公式。

对于改进型波形钢腹板箱梁，采用钢板代替了混凝土下翼缘板，上翼缘仍采用混凝土结构，因此需采用剪力连接件将上翼缘与腹板相连。由于没有完全刚性连接件，翼缘与腹板交界面存在不同程度变形而产生滑移效应，进而影响组合梁的整体刚度和剪滞系数[12-15]。苗林等[13]利用Goodman弹性夹层分析法，将组合梁的应变分解，构建了结构平衡微分方程，研究双层组合梁弹性阶段的滑移、挠度及内力；冯建祥等[15]推导了考虑波形钢腹板界面滑移的波形钢腹板梁弹性弯曲微分方程。上述研究未分析滑移效应对箱梁正截面应力的影响。

综上所述，目前针对组合箱梁剪滞效应和滑移效应的研究多集中于传统箱梁结构，没有考虑波形钢腹板抗剪刚度的影响。对于改进型波形钢腹板箱梁主要是从剪滞效应或动力特性进行研究[4]，但是混凝土板与连接件之间的滑移效应会与剪滞效应作用共同影响箱梁横截面上正应力分布，进而影响剪滞系数。因此，本文考虑波形钢腹板剪切变形和界面滑移效应，采用能量变分法建立改进型波形钢腹板组合箱梁的控制微分方程，得到组合箱梁翼缘正应力、剪滞系数和挠度解析表达式。利用有限元模拟验证了本文提出的理论公式的正确性，进而分析了剪切抗滑移刚度对组合箱梁正应力、剪滞效应和挠度的影响，为该桥型剪滞效应计算和分析提供科学的理论依据。

1 滑移模型

对于改进型波形钢腹板箱梁，假定混凝土上翼缘与波形腹板钢梁在接触界面存在滑移且梁体变形仍为弹性变形，变形截面各自保持均匀的伸缩。同时，混凝土上翼缘板和钢箱梁连接紧密，即不考虑混凝土板的掀起且假定箱梁截面无竖向挤压变形，两者竖向挠曲变形完全相同。

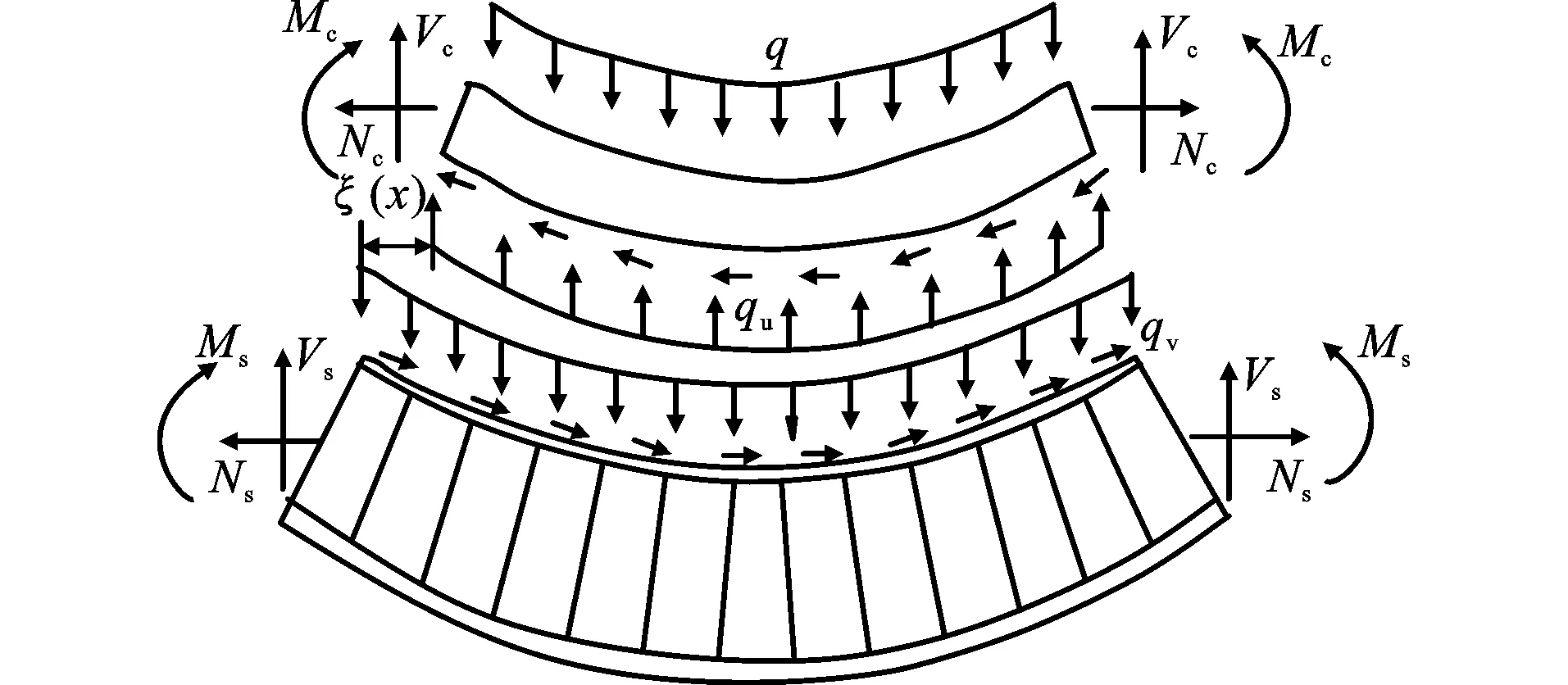
组合箱梁微段变形图如图1所示，其中，q为箱梁承受的均布荷载，Mc、Ms、Vc、Vs、Nc、Ns分别为组合箱梁中混凝土翼缘板与波形腹板钢箱梁的弯矩、剪力和轴力，qu和qv分别为组合箱梁的层间竖向力与层间剪力，ξ(x)为混凝土上翼缘板与钢梁在水平方向的滑移纵向位移差函数，即组合箱梁的界面滑移量，其表达式为

ξ(x)=ξs(x)-ξc(x)

(1)

(2)

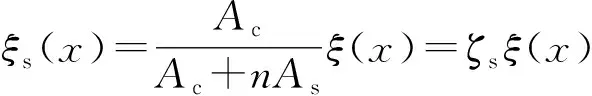
(3)

式中:ξc(x)、ξs(x)分别为混凝土板和波形腹板钢梁的纵向位移量；ζc、ζs分别为混凝土翼缘板与波形腹板钢箱梁的纵向滑移系数；n为钢材弹性模量Es与混凝土弹性模量Ec之比；As、Ac分别为钢板、混凝土截面面积。

2 控制微分方程的建立与求解

2.1 基本假定

为方便公式推导与计算，在竖向荷载作用下，考虑界面滑移效应与组合箱梁的变形特点，采用以下基本假定：

(1)由于波形钢腹板的“褶皱效应”，其纵向抗弯刚度很小，为简化计算，假定波形钢腹板不承受弯矩，只承受剪力作用，忽略波形钢腹板的纵向弯曲应变能。

(2)假设混凝土上翼缘和波形腹板钢箱梁的剪切抗滑移刚度与相对滑移量为线弹性关系，即V(x)=kξ(x)，其中V(x)为截面剪力分布，k为剪切抗滑移刚度；混凝土翼缘板和钢箱梁的剪切抗滑移刚度是由剪力连接件提供，由于箱梁截面和荷载对称，忽略混凝土翼缘板与箱梁的黏结作用及横向滑移变形。

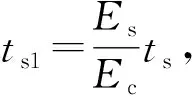
2.2 纵向广义位移函数定义

利用变分原理对改进型波形钢腹板组合箱梁进行分析，引入广义纵向位移函数u(x,y,z)和挠度函数w(x)。组合箱梁的纵向位移由4种变形组成：①弯曲变形；②混凝土板和箱梁相对转角φ(x)；③混凝土上翼缘板和钢下翼缘板剪滞效应产生的截面纵向位移分布差；④上翼缘板与腹板交界面由于剪力连接件剪切变形产生的界面滑移变形。利用位移叠加原理，叠加以上4种位移变形可以得到改进型波形钢腹板组合箱梁下翼缘板、上翼缘悬臂板和非悬臂板各处任意一点纵向位移u0(x,y,z)、u1(x,y,z)、u2(x,y,z)的计算公式，即

(4)

式中：hc、hs分别为上、下翼缘板形心到组合箱梁形心的距离；f0(y,z)、f1(y,z)、f2(y,z)分别为下翼缘板、上翼缘板悬臂板、上翼缘板非悬臂板的剪滞翘曲位移函数；U(x)为组合箱梁翼缘板最大纵向位移差函数。

组合箱梁腹板弯曲变形后的转角φ(x)表达式为

(5)

式中：Gw为波形钢腹板的有效剪切模量；Aw为波形钢腹板横截面面积和。

f(y,z)为组合箱梁剪滞翘曲位移函数，本文选取精度较高且便于计算的二次函数作为组合箱梁的翘曲位移差函数，其表达式为

(6)

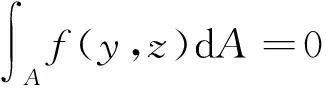
2.3 组合箱梁的总势能方程式建立

下翼缘板、上翼缘悬臂板和非悬臂板正应变εb,0、εb,1、εb,2表达式分别为

f0(y,z)U′(x)

(7)

f1(y,z)U′(x)

(8)

f2(y,z)U′(x)

(9)

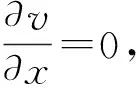
(10)

(11)

(12)

式中：v0、v1、v2分别为下翼缘板、上翼缘悬臂板和非悬臂板的横向变形。

根据基本假定3，上、下翼缘板应变能Vbi表达式为

(13)

式中：σbi、εbi、τbi、γbi分别为上下翼缘板的正应力、正应变、剪应力、剪应变；Gc为混凝土的剪切模量；i=1，2，分别对应上翼缘板、下翼缘板。

(14)

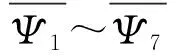
(15)

式中：tw为腹板厚度。

(16)

(17)

式中：M(x)为组合梁弯矩分布。

组合箱梁的总势能Π表达式为

(18)

2.4 控制微分方程求解

根据变分原理，当外力作用在平衡稳定的弹性体上时，真实位移对应的应变能最小，即δΠ=0(δ表示偏微分，下同)。对式(18)求变分，可求出微分控制方程(19)～(21)及边界条件式(22)～(24)。

(19)

(20)

(21)

(22)

(23)

(24)

将公式(19)～(24)化简并分离变量，可以得到ξ(x)和U(x)的控制微分方程分别为

ξ(4)(x)+B1ξ″(x)+B2ξ(x)=C1V(x)

(25)

U(4)(x)+B1U″(x)+B2U(x)=C2V(x)

(26)

式中：B1、B2、C1、C2表达式见文献[16]。

式(25)、(26)特征方程为

r4+C1r2+C2=0

(27)

式(27)的根为

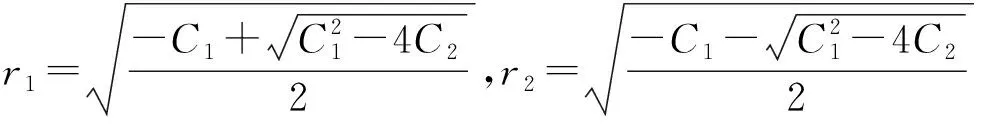
ξ(x)=D1sh(r1x)+D2ch(r1x)+D3sh(r2x)+

D4ch(r2x)+S(x)*

(28)

U(x)=J1[D1sh(rx)+D2ch(r1x)]+J2[D3sh(r2x)+

(29)

式中：D1～D6、J1～J3表达式见文献[21]；S(x)*为与剪力有关的特解。

S(x)*表达式为

(30)

3 算例验证

3.1 均布荷载下组合箱梁桥挠度和剪滞系数公式推导

对于受均布荷载的组合箱梁，其荷载条件为

(31)

组合箱梁边界条件为

(32)

将式(20)进行两次积分，联立式(5)可得组合箱梁挠度w(x)表达式为

(33)

根据式(31)～(33)，求出待定系数D1～D8后，可得到混凝土翼缘板与钢箱梁的滑移函数ξ(x)、翼缘板纵向位移差函数U(x)表达式。

由ξ(x)、U(x)和f(y,z)表达式，可得到考虑界面滑移效应及剪滞效应的上翼缘板截面正应力σu,x及下翼缘板截面正应力σl,x表达式，分别为

f1/2(y,z)U′(x)}

(34)

f0(y,z)U′(x)}

(35)

界面滑移效应会影响上、下翼缘板的正应力分布，因此在计算考虑滑移效应的组合箱梁剪滞系数时，将翼缘板上求得的考虑剪滞效应及滑移效应的实际正应力沿翼缘板宽度方向进行积分，除以翼缘板宽度作为初等梁的平均正应力，得到上、下翼缘板剪滞系数λupper、λlower的计算公式，即

(36)

(37)

3.2 均布荷载下组合箱梁的有限元计算方法

本文算例中的改进型波形钢腹板组合箱梁为简支结构，l=40 m，梁截面各部分的细部尺寸见图2。材料参数取为：Ec=34.5 GPa，Es=206 GPa，泊松比μc=0.2(混凝土)，μs=0.3(钢材)。剪力连接件为d=20 mm的圆柱头焊钉，材质为4.6级，焊钉的抗拉强度f=215 MPa，剪切系数γ=1.67，栓钉纵向间距为100 mm，每排布置2根栓钉，计算得到单位长度上剪切抗滑移刚度为2.084 GPa。

建立空间有限元模型，上翼缘板采用实体单元，下翼缘板与波形腹板采用壳单元，利用弹性连接单元模拟栓钉剪力键。均布荷载q=150 kN·m-1，分别施加在腹板位置处的上翼缘板左右两侧。网格划分见图3，计算点布置见图2。在有限元模型中，利用印刻功能考虑翼缘和腹板单元耦合来忽略滑移效应；滑移效应则是在翼缘和腹板单元之间添加弹性连接单元，通过弹性刚度考虑其效应的。

图4对比了采用理论解和考虑与不考虑滑移的有限元模型计算的组合箱梁挠度变形曲线。由图4可知，理论方法计算的挠度值总体略大于考虑滑移的有限元解，不考虑滑移计算的挠度最小，说明采用本文理论方法计算结构挠度时使结构设计更偏于安全。理论解与考虑滑移的有限元结果的相对误差在支座截面附近较小，在跨中截面处达到最大，最大相对误差为5.42%。

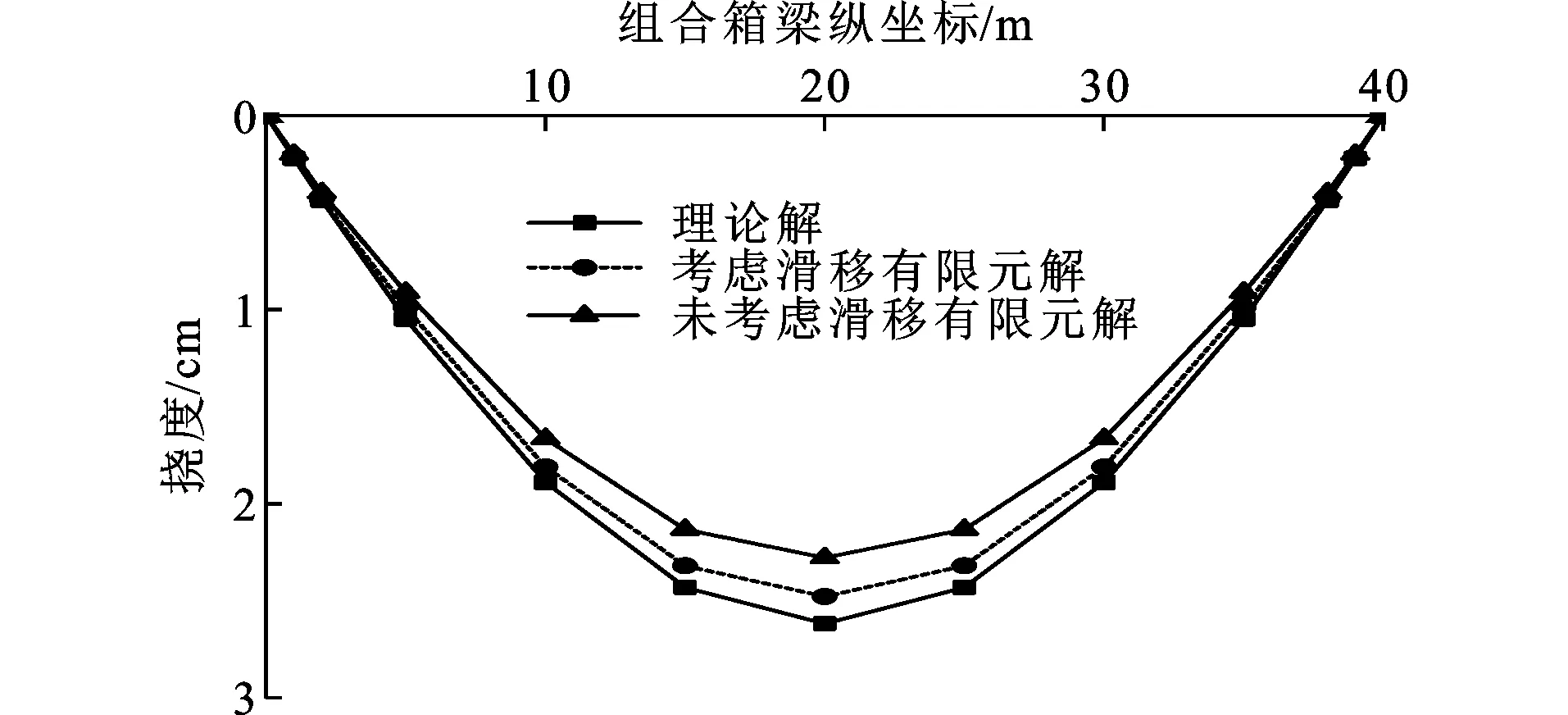
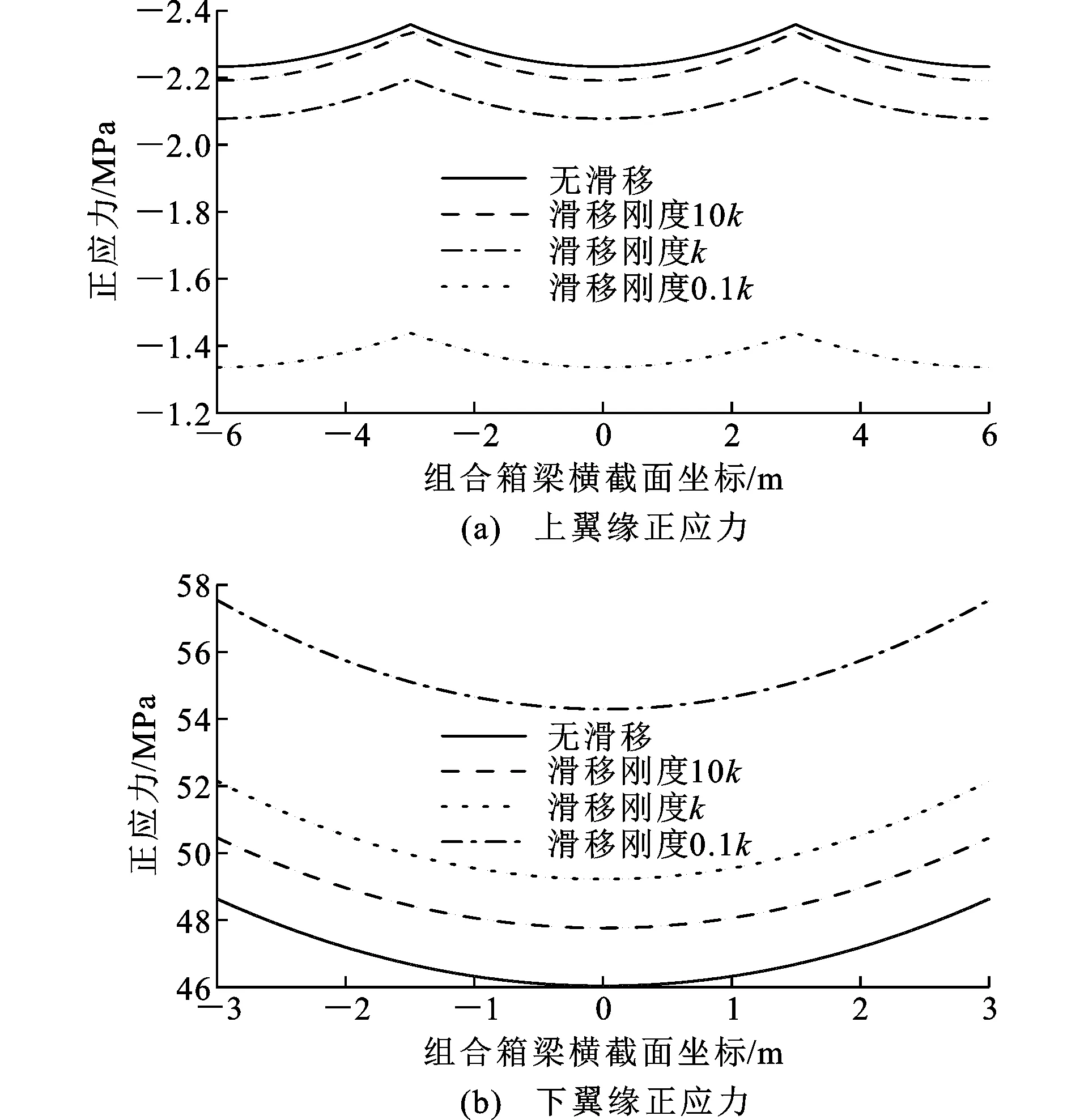
图5为跨中截面上、下翼缘板正应力值的理论解与数值解(拉为正值，压为负值)。由图5可以看出，上、下翼缘的正应力最大值均出现在翼缘板与腹板的交界处。组合箱梁在考虑界面滑移的影响下，跨中截面各计算点处截面正应力理论解与有限元解较为吻合，上、下翼缘处正应力相对误差均小于5%，验证了本文理论公式的正确性。考虑界面滑移效应后，上翼缘处正应力减小，下翼缘板正应力增大，与不计滑移相比，上翼缘正应力最大相对误差为7.44%，下翼缘正应力最大相对误差为6.79%。同时，由图5看出考虑滑移的有限元计算结果均在本文理论解和不考虑滑移的有限元结果之间，对比得出本文计算结果更偏于保守。

4 参数分析

根据第2节推导的理论公式，波形钢腹板组合箱梁桥的位移受滑移效应影响，位移变化会引起翼缘板应变和应力变化，进而影响剪滞系数取值。滑移效应与剪切抗滑移刚度有关，因此本文基于推导的理论公式，研究剪切抗滑移刚度对改进型波形钢腹板组合箱梁桥挠度、剪滞系数及上、下翼缘板正应力的影响。

保持箱梁材料、截面参数、荷载形式与第3.2节一致，改变组合箱梁的剪切抗滑移刚度(分别取0.1k、k、10k，k=2 048 MPa)，分析组合箱梁考虑滑移效应后上、下翼缘板的正应力、剪滞系数和箱梁桥挠度变化规律。

4.1 剪切抗滑移刚度对组合箱梁正应力的影响

图6为剪切抗滑移刚度对组合箱梁翼缘正应力影响曲线。由图6可知，在均布荷载作用下，随着剪切抗滑移刚度的下降，上翼缘板的正应力逐渐减小，下翼缘板的正应力逐渐增大，翼缘板正应力受滑移效应影响而重新分布。当剪切抗滑移刚度取k和10k时，翼缘处最大正应力相对不考虑滑移的理想状态相对误差均能控制在7%以内，当剪切抗滑移刚度值取0.1k时，翼缘处的最大正应力相对不考虑滑移时的正应力相对误差可以达到39.02%和17.81%，说明当剪切抗滑移刚度过低时，组合箱梁整体抗弯刚度下降很大，翼缘处的正应力变化显著。

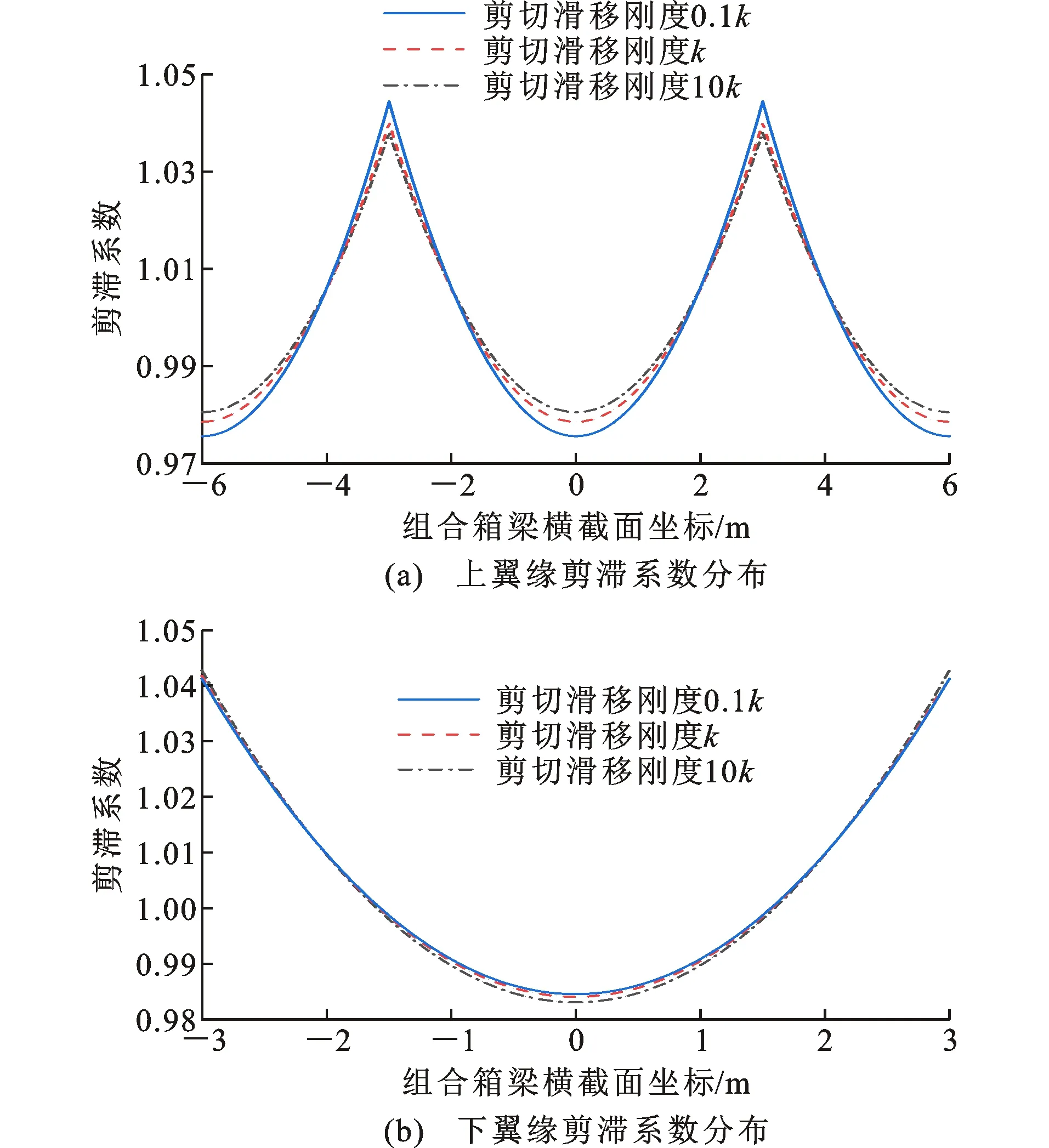
4.2 剪切抗滑移刚度对组合箱梁剪滞系数的影响

均布荷载作用下，上、下翼缘板剪滞系数如图7所示。结果表明，不同的剪切抗滑移刚度下翼缘板剪滞系数沿横截面的分布形式类似，且均在翼缘板与腹板交界处取得峰值。随着剪切抗滑移刚度增大，上翼缘峰值剪滞系数由1.044 3降低至1.037 9，下翼缘峰值剪滞系数由1.041 2增长至1.042 7。分析可知，相较于下翼缘，上翼缘剪滞效应受剪切抗滑移刚度的影响更加显著，且剪切抗滑移刚度越小时，横截面上正应力分布越不均匀。总体来看，剪切抗滑移刚度对改进型波形钢腹板组合箱梁的剪滞效应影响较小，变化幅度均在1%以内，基本可以忽略。

4.3 剪切抗滑移刚度对组合箱梁挠度的影响

图8、9为取剪切抗滑移刚度ks分别为0.1k、0.5k、k、2k、10k时计算出的组合箱梁跨中挠度以及纵向挠度分布。

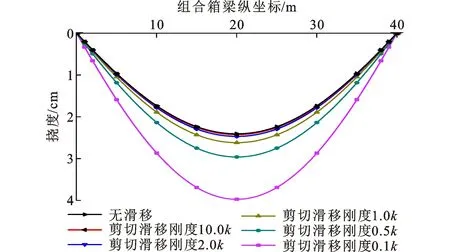
由图8、9可知，在考虑界面滑移产生的附加挠度后，组合箱梁的跨中最大挠度相较于无滑移的理想状态增长了8.8%，当剪切抗滑移刚度为0.1k时，组合箱梁跨中的最大挠度增长了65%。分析可知剪切抗滑移刚度对波形钢腹板组合箱梁的挠度有很大影响，当剪切抗滑移刚度较小时，随着剪切抗滑移刚度的增大组合箱梁挠度显著减小；当具有足够的剪切抗滑移刚度时，继续增大剪切抗滑移刚度对组合箱梁挠度的影响将十分有限。

5 结语

(1)基于能量变分法的理论公式与数值模拟结果的相对误差较小，为改进型波形钢腹板组合箱梁的剪滞效应及变形分析提供了理论基础。

(2)随着剪切抗滑移刚度的降低，上翼缘处正应力逐渐减小，下翼缘处的正应力逐渐增大，上、下翼缘处正应力受滑移效应的影响重分布。

(3)剪切抗滑移刚度对组合箱梁的挠度有较大影响。保证界面连接处足够的剪切刚度能够有效控制滑移变形所产生的附加挠度。

(4)均布荷载作用下，剪切抗滑移刚度对改进型波形钢腹板组合箱梁的剪滞效应影响很小，可以忽略。