带翼缘截面混凝土受压区等效应力图系数研究
任 伟,李敬泉,李晓路
(1. 长安大学旧桥检测与加固技术交通运输行业重点实验室,陕西西安 710064; 2. 广东省交通运输规划研究中心,广东广州 510101)
0 引 言
钢筋混凝土压弯构件正截面极限承载力的计算方法是基于平截面假定的计算理论得出的,在实用计算中,受压混凝土的应力分布可以通过引入矩形应力图系数α(等效应力图应力与混凝土应力-应变曲线峰值应力的比值)和β(等效应力图高度与中和轴到受压边缘距离的比值)将其等效为矩形应力图。该方法概念清晰,易于建立平衡方程,不需要了解混凝土应力分布的准确形状。
《混凝土结构设计规范》中直接给出了不同强度等级混凝土受压区等效矩形应力图系数α和β的取值[1]。相关文献也对其计算方法进行了说明,并对某些强度等级的等效矩形应力图系数进行了试算,如过镇海[2]在《钢筋混凝土原理》中推导并给出了C50以下的混凝土受压区等效矩形应力图系数表达式。张树仁等[3]在理论分析和试验研究的基础上,针对钢筋混凝土圆、环形截面偏心受压构件提出了在强度计算中采用混凝土矩形应力块换算系数的设计建议。王文炜[4]从混凝土正截面受弯承载力基本假定出发,推导出了C50以下混凝土受压区等效矩形应力图系数表达式。王庆华等[5]采用MATLAB数学工具给出了三角形截面、圆形截面的受压区等效矩形应力图系数。刘凤翰[6]对正截面设计中α和β等系数进行分析研究,并提出非矩形四边形梁等其他形式截面采用α和β等系数的计算方法。丁亚进等[7]采用力的等效原理,通过不定积分计算器推导出普通和高强混凝土受压区等效矩形应力图系数通用表达式。朱莉萍等[8]对圆形截面偏心受压构件的压区混凝土等效应力图形的特征参数做了详细计算分析,提出了参数取值的建议。孙铁锋等[9]利用换元积分等方法,对矩形、圆形、等腰三角形截面的压区混凝土等效矩形应力图特征参数计算方法的简化进行了探讨。Naaman[10]对T形截面进行了讨论,重点对何时可以将T形截面简化成矩形截面进行了论述。Singh等[11]提出在IS 456—2000中,对于等级高于M55的混凝土,给定的设计参数可能不适用,他通过试验应变值计算应力块参数K(强度折减系数)和k2(合压力深度系数),并给出了等效应力块参数的计算方法。
然而,大量的混凝土桥梁多采用带翼缘的T形、箱形、π形和工字形截面,该类截面与矩形截面相比,几何形状明显复杂了许多[12-17]。系数α和β与诸多因素有关,其中截面形状的几何要素为主要敏感变量之一[18-19],因此上述截面的计算不能盲目按规范建议的矩形截面取值。
因此,本文基于矩形截面的静力等效算法,借助MATHEMATICA强大的符号运算功能,对带翼缘截面混凝土受压区等效应力图系数α和β进行解析分析,并针对解析解答过于冗长的问题,采取了数据变换拟合的方法,给出了简化计算公式。本文推荐的简化公式为相关工程技术人员提供了直接可用的简化算法,也可为规范标准的修订提供科学支撑。
1 带翼缘截面等效应力图系数
1.1 矩形截面等效应力图系数
在混凝土正截面强度计算中,混凝土应力-应变关系被简化为曲线段和直线段,为进一步简化计算,又采用α和β对混凝土应力分布进行了矩形等效替换。等效应力图的换算原则为:①等效前后合力大小不变;②等效前后合力作用位置不变。
现有成果显示,当正截面混凝土极限压应变εcu=0.003 3,混凝土压应力达到抗压强度设计值且压应变ε0=0.002时,α=0.969,β=0.824。当混凝土强度等级大于C50时,可按表1取值。

表1 等效矩形应力图系数Table 1 Equivalent Rectangular Stress Diagram Coefficients
1.2 带翼缘截面等效应力图系数
1.2.1 截面简化
从已有的研究成果来看,现在的截面等效应力图系数主要针对矩形截面、圆形截面和三角形截面[5-9,20],对于桥梁结构中常用的带翼缘截面应力图系数未见相关研究报道。目前常见的带翼缘截面有:T形截面(矮T梁)、箱形截面、π形截面、工字形截面等。在进行正截面承载力分析时,由于受拉区混凝土不计入工作,因此可将上述截面一并简化为T形截面进行正截面受力分析。
截面简化的基本假定包括:
(1)平截面假定:截面的平均应变始终较好地保持平面假定。
(2)不考虑受拉区混凝土的作用。
(3)混凝土本构关系依据《混凝土结构设计规范》[1]取值。
(4)钢筋应力-应变关系采用理想双折线本构模型。
(5)忽略翼缘有效工作宽度的影响,按初等梁理论进行分析。
1.2.2 截面分析
混凝土的受压应力-应变关系按式(1)~(5)取用[1]。
当εc≤ε0时
(1)
当ε0<εc≤εcu时
σc=fc
(2)
(3)
ε0=0.002+0.5(fcu,k-50)×10-5
(4)
εcu=0.003 3-(fcu,k-50)×10-5
(5)
式中:σc为混凝土压应变为εc时的混凝土压应力;fc为混凝土轴心抗压强度设计值;ε0为混凝土压应力达到fc时的混凝土压应变,当ε0小于0.002时,取0.002;εcu为正截面混凝土极限压应变,εcu计算值大于0.003 3时,取0.003 3;fcu,k为混凝土立方体抗压强度标准值;n为系数,计算值大于2时,取2。
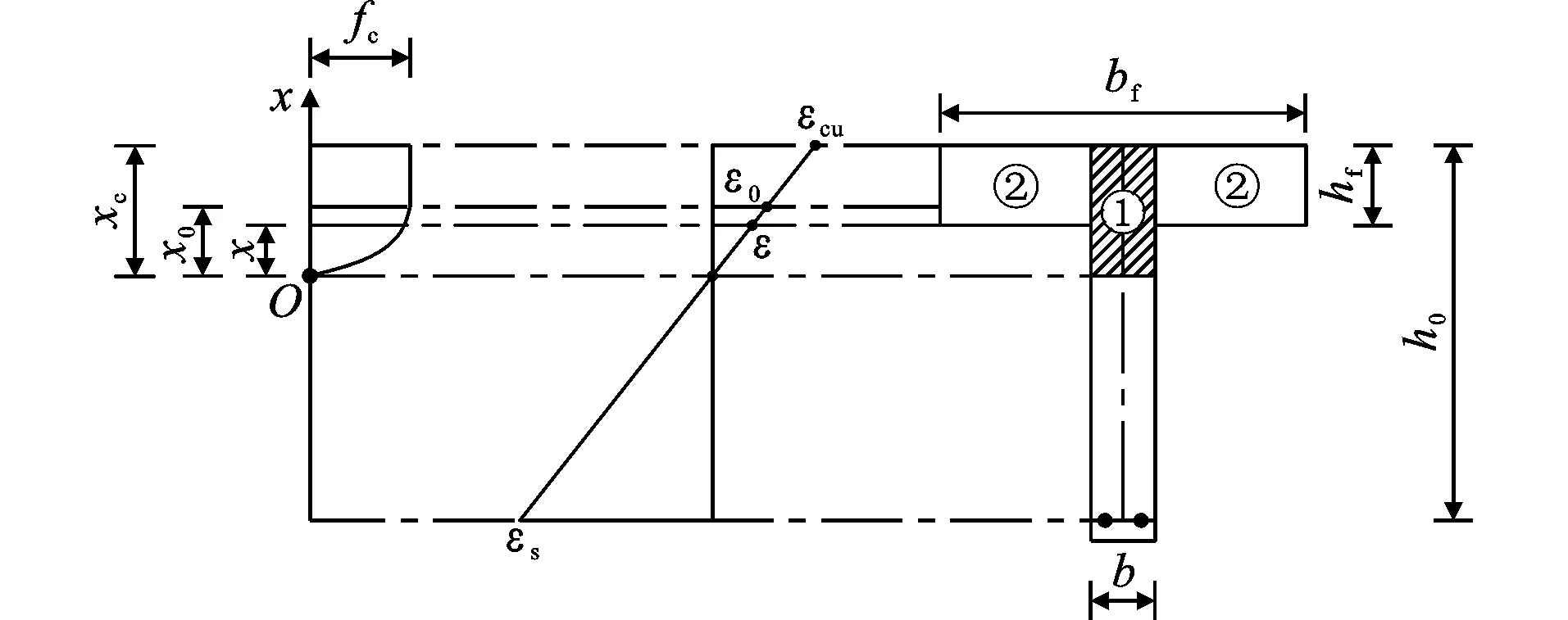
根据图1中的截面应力、应变及几何关系,将截面划分区域进行分析,图中εs为钢筋应变。受压区腹板为区域①,翼缘部分为区域②。区域①的合力F1为

(6)

区域②的合力分两种情况,分别为F2和F3。
当x0在腹板时
F2=fc(bf-b)hf
(7)
当x0在翼板时

(8)
式中:hf为T梁翼缘板厚度;bf为翼缘板宽度。
区域①的合力矩M1为
(9)
区域②的合力矩分两种情况,分别为M2和M3。
当x0在腹板时
(10)
当x0在翼板时
(11)
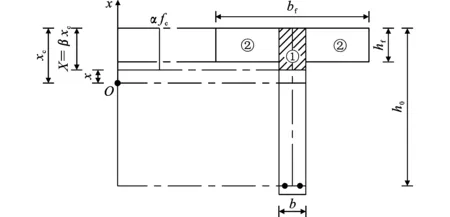
1.2.3 等代荷载分析
图2为等代荷载作用截面应力、应变及几何关系,分析时根据等代压应力图的分布范围分两种情况讨论。
当X=βxc在腹板时
F4=αfcXb
(12)
F5=αfchf(bf-b)
(13)
(14)
(15)
当X=βxc在翼缘时
F6=αfcXbf
(16)
(17)
式中:F4、M4分别为区域①的合力、合力矩;F5、M5分别为区域②的合力、合力矩;F6、M6分别为合力、合力矩。
1.2.4 求 解
方程求解也分情况进行。
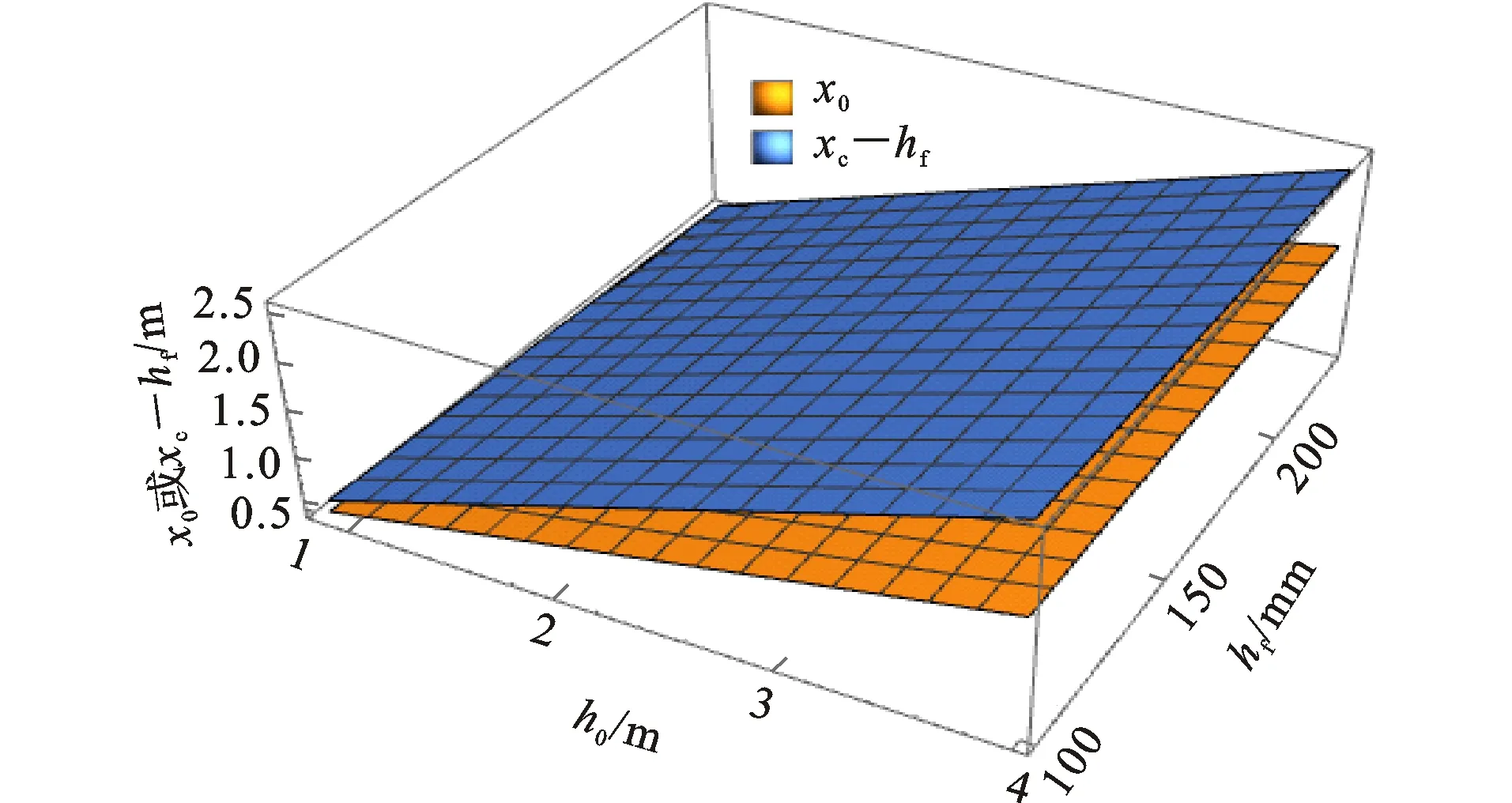
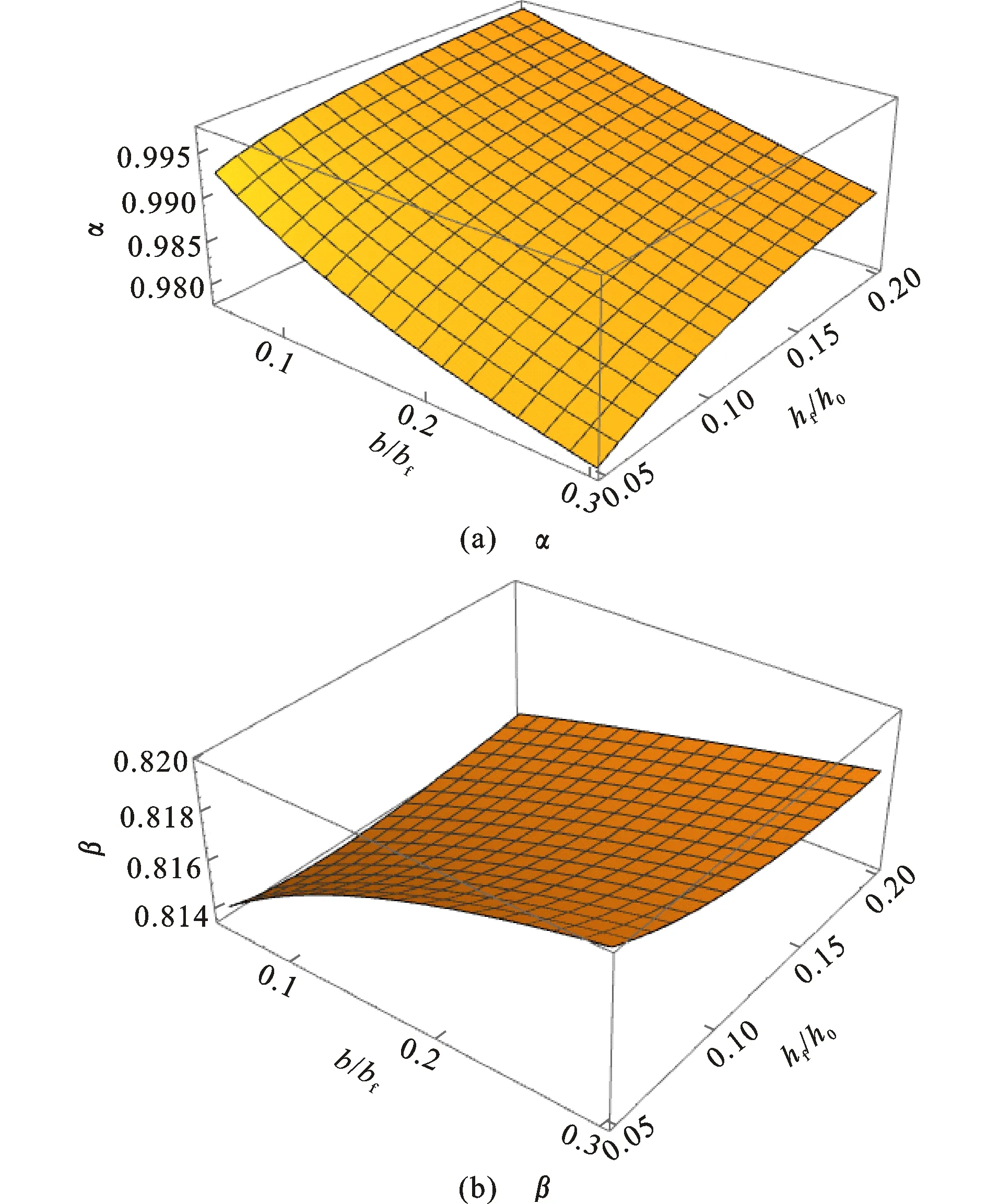
当x0在腹板,即x0 (18) 当x0在翼缘,即x0≥xc-hf时 (19) (20) 根据图1可以得出 (21) (22) 取ε0为0.002,εcu为0.003 3,εs为0.001 675,得 x0=0.402 414h0 (23) xc=0.663 984h0 (24) 将常规截面几何构造尺寸代入式(23)、(24),并绘制出图3。可以看出x0 式(18)有两组解,根据公路桥梁T梁标准图的取值h=1 750~2 500 mm,bf=2 200mm,b=160 mm,翼缘板平均厚度hf=180 mm。将式(18)得到的α和β的两组解绘制于图4,可以看出图4(b)为不合理解,应舍去。由图4(a)可以看出,在其他几何参数不变的情况下,单因素h0对α和β的影响非常小。 根据式(18)的有效解,将α和β与b/bf和hf/h0的关系绘制于图5,为了更加清晰地展示它们的变化规律,进一步给出了图5的切面图,详见图6和图7。由图6和图7可以看出:α随着b/bf的增大而减小,随hf/h0的增大而增大,总体呈曲面变化;β随着b/bf的增大而增大,随hf/h0的增大呈扭曲线变化,总体呈微扭曲面变化。 表1给出了混凝土等级大于等于C50的等效矩形应力图系数,其中带翼缘截面理论值为在几何参数为定值情况下式(18)的解析解。可以看出,无论是参考文献中给出的理论值还是规范值,均无法准确代替带翼缘截面的计算。 将表1中带翼缘截面理论值随fcu,k的变化情况绘制于图8,变化曲线呈现出明显的二次曲线规律。将数据点分别进行拟合,得到式(25)和(26),这两式的拟合度非常高,判定系数R2=1。 α和β的混凝土强度调整系数γα和γβ为 γα=0.999 9+1.252 2×10-4fcu,k- (25) γβ=1.067 8-4.148 6×10-4fcu,k- (26) 式(18)可以给出本文讨论问题的解析解,但是该解非常繁琐,不便于应用。因此本文通过改变b、bf等几何参数,应用解析解在有限域内得出256个数值解,再通过数据拟合的方法给出式(18)的替代算法,如式(27)、(28)所示。通过以上变换得到的式(27)、(28)的拟合度均较高,式(27)的R2=0.960 866,式(28)的R2=0.966 295。 (27) (28) 式中:当混凝土等级小于等于C50时,γα和γβ取1;当混凝土等级大于C50时,γα和γβ按式(25)、(26)进行计算。 为比较本文解析算法、推荐公式与规范值的区别,验证推荐简化算法的精确度,选取了目前桥梁结构常采用的T型梁、矮T梁和小箱梁截面(图9)进行算例分析,计算结果列于表2。可以看出,目前的规范建议值不太适用于带翼缘的截面,尤其是当混凝土等级较高时。此外,推荐简化算法的精确度较高,完全可以替代解析解的应用。 表2 算例计算结果Table 2 Example Calculation Results (1)给出了带翼缘截面等效矩形应力图系数的解析解,通过算例对比发现目前的规范值无法准确代替带翼缘截面的计算。 (2)在解析解的基础上进行了几何参数讨论,得出α和β随b/bf和hf/h0的变化呈曲面和微扭曲面的变化特征。 (3)为提高解析公式的可应用性,借助数据拟合的方法对本文得出的解析解进行了数值化后再拟合,给出了α和β的简化计算方法,由此得到的拟合公式拟合度较高。 (4)通过算例对比分析得出,α和β的规范建议值与本文解析解偏差分别为4.8%和2.2%。2 参数分析
2.1 有效解

2.2 截面几何参数分析

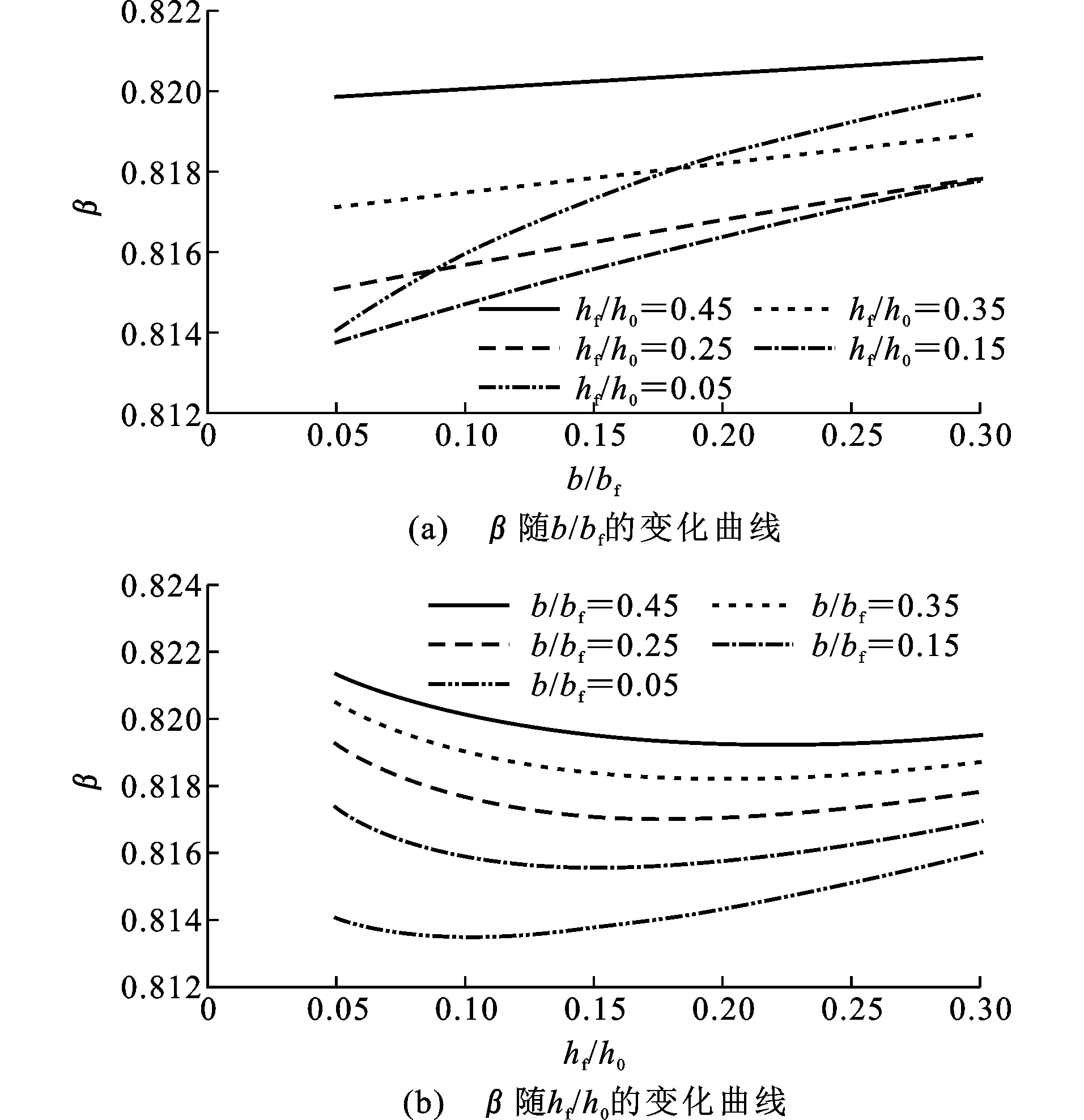
2.3 材料参数分析
3 推荐公式和算例
3.1 推荐公式

3.2 算 例

4 结语

