一种三次插值曲面的光滑拼接
师 晶
(闽南理工学院 信息管理学院,福建 石狮 362700)
作为计算机辅助几何设计(CAGD)的重要内容,曲面造型不仅在理论上具有很高的研究价值, 而且在航空航天、工程设计、动画制作及计算机图形设计等领域有着广泛的应用。随着科学技术的发展,传统的曲面造型方法已无法满足曲面复杂化和多样化的需要[1]。 因此,曲面拼接技术应运而生,其理论思想和构造方法几乎渗透了所有的学科。
在计算机辅助几何设计(CAGD)中,用B 样条或T 样条构造曲面因拟合效果好、 程序便于编写而成为曲面造型的重要方法。但是,当B 样条曲面的控制顶点发生变化时, 整个曲面形状容易发生扭曲和变形,且随着阶数升高,构造曲面时的计算过程越来越复杂,曲面形状的可调性越来越差[2-3]。 另外,在对多变等参矩形域进行几何裁剪时, 若采用T 样条构造曲面,则会产生一些难以处理的奇点,且细分后不能保持仿射不变性[4-5],这些都不利于曲面造型[6-7]。 为了解决复杂曲面的拼接问题, 笔者研究了一种带形状参数的三次插值曲面的连续性问题, 利用三次插值曲线的几何性质和保凸性质, 得到了曲线间的C1和C2连续定理和曲面间的G1拼接定理,给出了曲面的拼接方法及步骤, 通过曲面造型算例验证了方法的有效性。
1 基础知识



2 曲线的性质


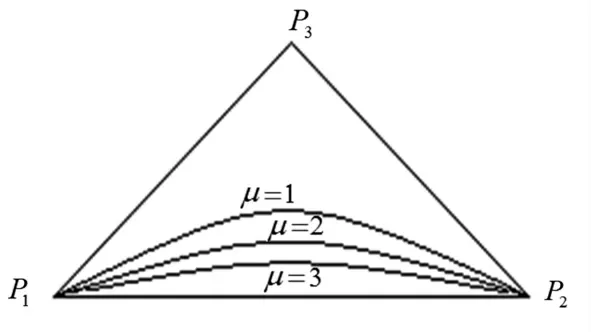
图1 λ =2,µ 改 变时的曲线H(λ , µ)

图2 µ = 0.2,λ改 变时的曲线H(λ , µ)
3 曲线拼接


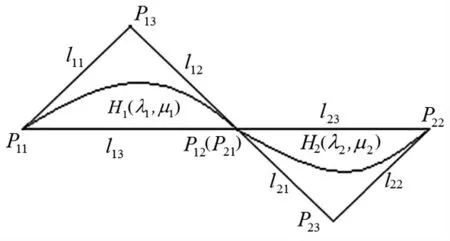
图3 () 为拐点时 H(λ , µ) 的连续性
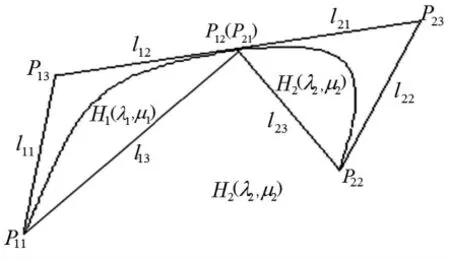
图4 ( )为非拐点时 H(λ , µ)满足保凸性的连续性


4 曲面的性质

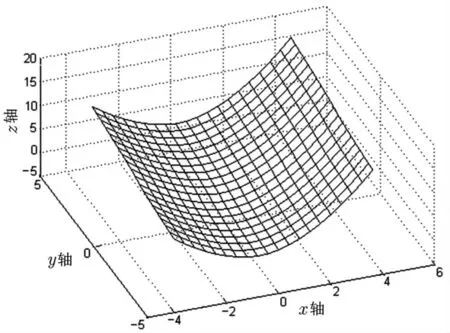
图5 3×3 个控制顶点的三次插值曲面

5 曲面拼接
设带有2 个形状参数的2 个三次插值曲面方程为


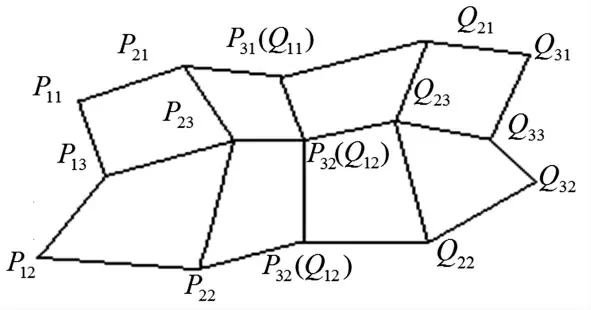
图6 2 个相邻三次插值曲面拼接网格



证明:与定理4、定理5 的证明过程类似,证明过程省略。
6 算法描述

步骤3:如果待拼接曲面片的个数大于2,转步骤2,直到生成所有的待拼接曲面片,再执行步骤4。否则,直接执行步骤4。
步骤4:通过修改各拼接曲面片的形状参数λk> 1,µk> 1(k=1,2)和法矢量模比例因子f调节拼接曲面的形状,获得满意的图形。
7 计算实例
在CAGD 中, 一张较复杂的曲面需要多个光滑曲面拼接。 利用三次插值曲面的拼接定理和插值算法,可以很方便地构造一些较复杂的曲面。为了说明插值算法的可行性和灵活性, 给出2 个曲面造型的算例。
7.1 算例一
由台灯曲面的构造可知, 台灯曲面需要多个曲面片拼接而成。
生成台灯灯罩曲面时, 先根据插值算法的步骤1 至步骤3 生成3 张待拼接曲面片。 由于这3 张待拼接曲面片在拼接处具有相同的切平面, 故不需生成过渡曲面。 再根据步骤4,通过修改各曲面片不同的形状参数值及法矢量模比例因子f,调节组合曲面的形状,获得满意的灯罩曲面图形。
重复以上曲面的拼接步骤, 可分别实现多张灯柱、 灯座曲面片的拼接, G1得到如图7 所示的台灯曲面造型。
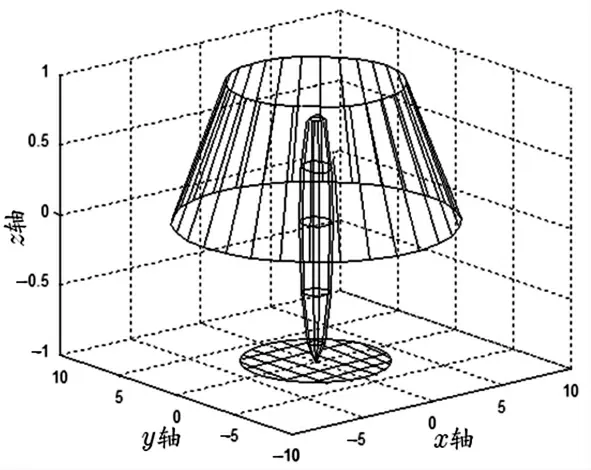
图7 台灯的曲面造型
7.2 算例二
由蘑菇板凳曲面的构造可知, 蘑菇板凳曲面需要多个曲面片拼接而成。
生成蘑菇板凳曲面时, 可先根据插值算法的步骤1 至步骤3,生成8 张待拼接曲面片。 这8 张待拼接曲面片在拼接处具有相同的切平面, 故不需生成过渡曲面。 再根据步骤4,通过修改各曲面片不同的形状参数值及法矢量模比例因子f调节组合曲面的形状,获得如图8 所示的蘑菇板凳曲面造型。
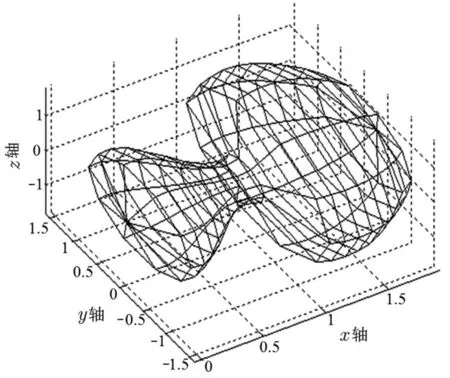
图8 蘑菇板凳的曲面造型
8 结束语
通过研究一种三次插值曲线的参数连续性,得到了这种曲线间的 C1和 C2连续条件。利用曲线的连续性得到了三次插值曲面的边界性质、凸包性、几何不变性等性质,给出了曲面间 C1的拼接定理及插值算法。通过算例说明了算法的可行性和灵活性,增强了三次插值曲线的曲面造型能力。

