扩张状态观测器下的FFSR末端轨迹跟踪控制

陈志华，胡安正

（1.襄阳汽车职业技术学院，湖北 襄阳 441021；2.湖北文理学院物理与电子工程学院，湖北 襄阳 441053）

1 引言

空间机器人，作为一种智能操作系统，能够高效地执行航天探测、在轨维修、空间建造等诸多任务，从而把航天员从复杂的太空环境中解放出来，近年来发展迅速且得到了航天人员以及控制领域专家学者的广泛关注[1−3]。根据基座的控制方式的不同，空间机器人的控制可分为基座位置受控、基座姿态受控、基座位姿受控和自由漂浮四种模式[4]。根据控制空间的不同，空间机器人的控制又可分为关节空间控制即通过对关节角的控制实现轨迹跟踪，以及任务空间控制即直接对机械臂末端控制以实现机械臂抓手的轨迹跟踪[5]。自由漂浮空间机器人（Free Floating Space Robot，FFSR）任务空间轨迹跟踪控制由于具备无需额外负载燃料、姿态灵活可调整、直接控制末端更符合实际工程需求等优点，逐步发展成为空间机器人控制领域研究重点。文献[6]针对模型参数不精确条件下的FFSR任务空间轨迹跟踪控制问题，提出了一种逆链逼近的自适应控制方法，实现了机械臂末端轨迹的精确跟踪控制；文献[7]考虑FFSR的模型误差，提出一种基于SDRE的末端轨迹跟踪控制方法，在实现了末端轨迹精确跟踪的同时考虑了输出力矩的优化；文献[8]利用神经网络的逼近特性和自适应控制器的学习特性，提出了一种自适应神经网络控制方法，实现了FF⁃SR的末端轨迹跟踪；文献[9]基于拉盖尔模型提出了一种离散模型预测控制方法，实现了FFSR末端的位置和速度跟踪。

在上述文献的研究中，均较好的实现了FFSR的任务空间轨迹跟踪控制，且考虑了模型参数以及外部干扰等复杂因素，但在控制系统设计上均需实时测量关节角和末端的位置信息以及速度信息，而空间机器人多处于低速运动状态、空间环境噪声大，速度测量易出现较大误差，且测速系统将增加系统质量和运行成本，引入观测器是一种较好解决方案。

文献[10]针对控制力矩受限条件下的空间机械臂轨迹跟踪控制问题，采用速度滤波器对速度信号进行估计，提出了一种自适应控制方法；文献[11]采用神经网络观测器对系统速度信息进行估计，提出了一种神经网络自适应鲁棒控制方法；文献[12]基于自抗扰技术，设计了扩张状态观测器，并结合模糊控制实现了机械臂的轨迹跟踪控制。文献[10−12]虽然解决了测速问题，但其主要针对空间机器人关节空间轨迹跟踪控制，而对于FFSR系统，由于基座位置易受反作用力运动，因此即便实现了关节角的精确跟踪，仍会由于基座位姿的改变使末端轨迹跟踪产生误差。

综合考虑上述问题，针对存在模型参数不精确以及外部扰动等不确定性条件下的FFSR末端轨迹跟踪控制问题，提出一种基于扩张状态观测器的优化控制方法。

首先，在建立FFSR 关节空间动力学和运动学模型的基础上，采用增广向量法获得FFSR的伪线性状态空间方程；而后，设计扩张观测器对状态变量以及系统不确定项进行在线估计，并采用Lyapunov方法对所设计观测器的稳定性进行分析；进而，将观测器的输出作为控制器的输入，提出一种基于SDRE的优化控制方法，实现FFSR系统末端轨迹的精确跟踪控制。数值仿真证明了所提控制方法的有效性。

2 FFSR系统建模

不失一般性，单臂空间机器人通常由基座B0以及搭载在其上的若干连杆机械臂Bn以及末端抓手组成H0，机械臂与基座有且仅有一个连接点J1，如图1所示。

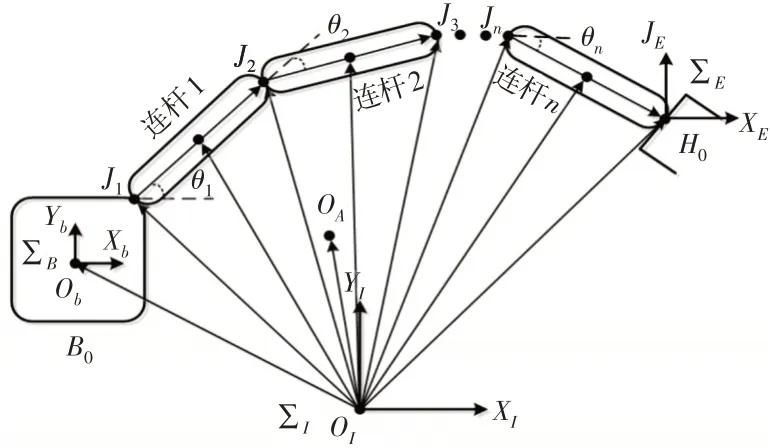
图1 单臂空间机器人系统结构图Fig.1 FFSR Structure Diagram

3 控制系统设计

在不测量角速度以及位置速度信息条件下，为实现FFSR系统末端轨迹精确跟踪控制，设计控制系统结构，如图2所示。

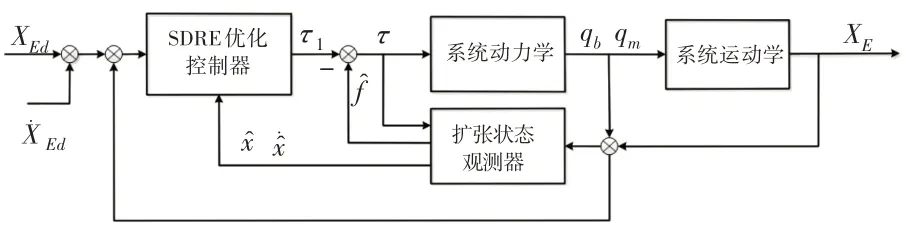
图2 控制系统结构Fig.2 Control System Structure

从图中可以看出控制系统设计的基本原理为：首先以角度和末端位置信息为输入，设计扩张状态观测器，对状态变量以及不确定项进行在线估计；进而，将观测器的输出作为控制器的输入，提出一种基于SDRE的优化控制方法，并将观测器获得的干扰观测量反馈至控制器中，获得最终控制律。

3.1 扩张状态观测器设计

为便于状态观测器的设计，需将式（5）所示的关节空间模型转变为状态空间模型。

根据式（4）可得：

定义增广状态变量x=[x1x2]T=[q̇m XE]T，输出变量y=XE，由式（5）、式（6）可得：

式中：x̂1、x̂2、f̂——状态观测以及误差观测向量；α1、α2、α3—正实数；ε>0；且多项式s3+α1s2+α2s+α3满足Hurwitz条件。

3.2 扩张状态观测器稳定性分析

为证明所设计的扩张状态观测器式（8）能够实现对状态变量以及误差变量的在线估计，即：当t→∞时，x̂1→x1、x̂2→x2、f̂→f。定义：

3.3 控制器设计

扩张状态观测器重点解决的是控制系统状态变量以及扰动变量的在线观测问题，为实现FFSR系统末端的轨迹跟踪控制，进一步针对式（7）所示的增广状态空间模型，将观测器的输出作为控制器的输入，提出一种基于SDRE的优化控制方法。

首先，不考虑系统模型不精确以及外部扰动带来的不确定性，则式（7）转化为：

定义FFSR系统期望末端轨迹为yd(t)，实际轨迹为y(t)，轨迹跟踪误差为e=yd(t)−y(t)，则按SDRE 控制原理[15]，针对形式如式（15）所示的状态空间模型，进一步结合状态观测器的观测结果，可设计控制器以及性能评价指标分别如下所示：

4 仿真实例

为验证所提控制方法的有效性，以文献[7]中的两连杆FFSR为例，进行Matlab∕Simulink数值仿真，空间机器人各项参数，如表1所示。

表1 系统参考惯性参数Tab.1 Inertial Parameters of System

表2 系统真实惯性参数Tab.2 Inertial Parameters of System

外部干扰为：τd=0.2+e+1.5ė（单位：N ⋅m，e=yd(t)−y(t)为跟踪误差）。设置仿真时长t=20.0s，仿真结果，如图3～图7所示。其中。FFSR系统末端轨迹跟踪情况。直接反应了所设计的控制器的控制效果，如图3所示。FFSR机械臂两个关节的输出力矩，反应了控制器输出力矩优化情况，如图4所示。扩张状态观测器分别对状态变量x1、x2以及系统不确定项f的观测范数值与实际范数值的跟踪情况，直接反应了扩张状态观测器的稳定性以及有效性，如图5～图7所示。

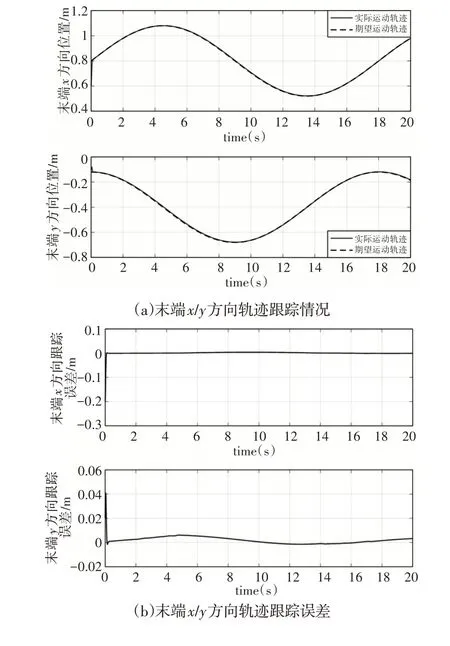
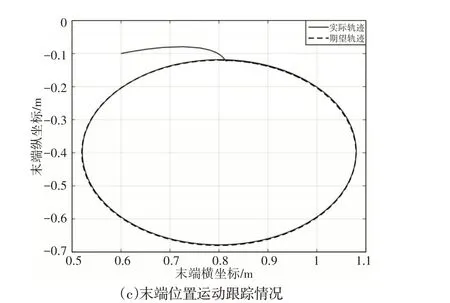
图3 末端轨迹跟踪情况Fig.3 End Track Tracking

在所设计的控制器作用下，FFSR机械臂末端轨迹跟踪情况，如图3所示为。其中，机械臂末端轨迹的x、y方向分量跟情况，如图3（a）、图3（b）所示。从仿真结果可以看出，期望轨迹xd为正弦运动函数、yd为余弦运动函数，在控制器作用下，实际运动分量与期望分量基本保持一致，跟踪误差均控制在0.01以内；机械臂末端在惯性坐标系下运动轨迹的直接反映，从仿真结果可以看出，期望运动轨迹为一椭圆，在控制器作用下，末端抓手迅速从初始轨迹点运动到指定点，且后续始终沿期望轨迹运动，如图3（c）所示。控制器输出力矩，如图4所示。从仿真结果可以看出，不仅考虑了控制器控制效果，即使机械臂末端实现精确轨迹跟踪，且同时考虑了控制器输出力矩的大小，所设计的控制器除初始力矩稍大外，整个控制过程输出力矩均较小，实现了能量的优化。

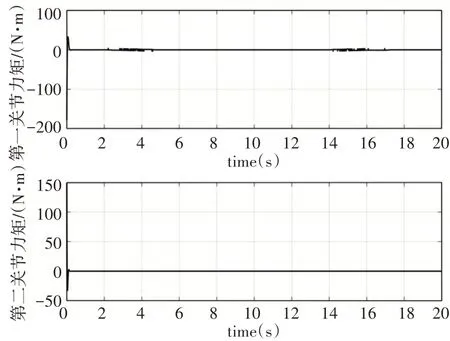
图4 关节控制力矩Fig.4 Joint Control Torque

设计扩张状态观测器的观测情况，如图5～图7所示。

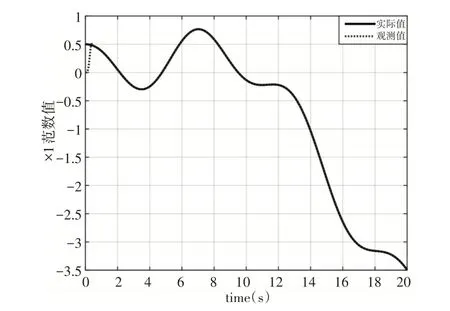
图5 状态变量x1观测情况Fig.5 Observation of State Variable x1

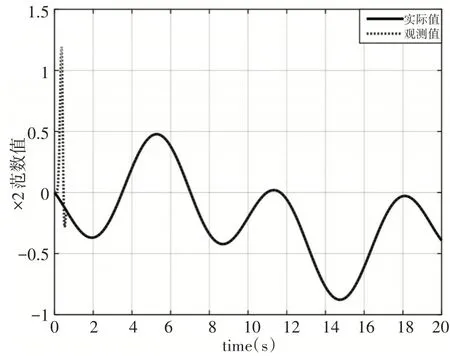
图6 状态变量x2观测情况Fig.6 Observation of State Variable x2

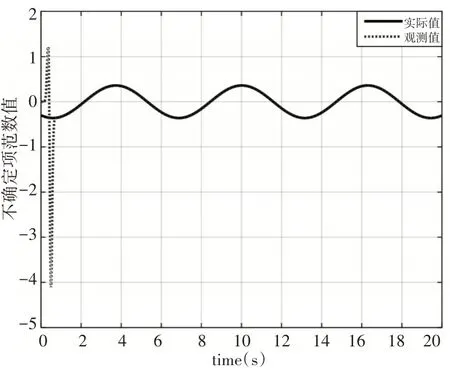
图7 不确定项观测情况Fig.7 Observation of Uncertainty

从仿真结果可以看出，所设计的扩张状态观测器能够较好的对系统状态变量以及系统不确定项的在线观测，即实现x̂1→x1、x̂2→x2、f̂→f。

5 结论

传统的空间机器人控制方法往往需实时测量关节角速度和末端的位置信息，而空间机器人多处于低速运动状态、空间环境噪声大，速度测量易出现较大误差，且测速系统将增加系统质量和运行成本。重点针对这一问题，同时考虑输出力矩的优化，提出了一种基于扩张状态观测器的优化控制方法，实现了末端抓手的精确轨迹跟踪控制。所提方法在以下几个方面具有一定优越性：（1）实现了对FFSR系统末端抓手的直接控制，较传统关节空间控制更具工程应用价值；（2）通过设计扩张状态观测器实现了对扩张状态空间方程的状态变量以及系统不确定项的在线观测，从而无需测量关节角速度以及末端位置信息；（3）基于SDRE控制原理提出的优化控制方法实现了能量的优化，控制力矩保持在较小范围。