Python在微积分教学中的应用
刘加菊
(湖南电气职业技术学院)
在信息技术被运用到教育领域后,“教与学”的形式均有所改变。线上教学不断普及下,学生对于课程选择与知识记忆方面有明显的需求。常规课堂教学也不再局限在板书上,为满足学生高效吸收知识的需要,教师应当通过各种方法优化授课效率。而Python可提供绘图功能,将各类定理、几何意义以动态图像的形式呈现出来,便于学生提炼知识,加强理解。
一、Python
(一)Python语言
Python在1991年诞生,时至今日已经成为一种主流编程语言,被用到爬虫与数据处理等方面。Python属于面向目标的解释性语言,便于维护、拓展、读取,并具有较强的可移植性。其分成2.x与3.x版本,直至2020年,前者已经不再维护,所以在教学实践中都要选择3.x版本。Python应用优势具体表现在标准库,覆盖范围广,而且支持跨平台运行。该标准库能够进行不同功能模块与函数运行,新内容也被保存在标准库中,让Python实际功能愈发强大。同时,Python是通过缩进方式将程序块结构进行分层处理,编写代码规格标准,便于读取使用[1]。
(二)Matplotlib
Matplotlib为Python中 的二维绘图库,工具相对齐全,包含等高线图、散点图、线图与柱状图等许多绘图函数,而且能生成图形动画等更加高端的绘制内容。另外,该绘图库也具备交互功能,支持动态调整绘图参数,这便于在教学过程中使用。而且此绘图库中还设有坐标轴与图例等多个子模块,可以给教师提供多种绘图样式。在面对三维绘图需要中,Python中在此绘图库的基础上,搭配mpl_tookits工具包,在不用设置大量代码的前提下,就能绘制出所需的三维图像。同时,此绘图库还设有Python图像用户界面的接口,能够与pyqt单元整合运用。选择Matplotlib生成图像,随后利用pyqt完成前端展示,这是Python实现可视化的主要方式。
(三)和微积分有关的Python库
首先,内置函数。Python中的内置函数,很多是为支持某个系统功能,实施逻辑判断以及类型转换。其在Python启动过程中一同加载,教师能直接应用。其次,math模块。例如三角函数、指数函数等众多符号运算、数值计算的函数,均未被归纳到内置函数范围内,直接保存在math库里。调取math库的函数中,教师能提前利用下达系统命令完成加载,随后以“math.函数名”实现调用。另外,也能直接提出“from math import *”的指令,完成math库的加载,之后便可编辑函数名称实现调用。而在实际应用中,如果进行同时加载,会令运行中的第三方库数量偏多,容易面临函数重名的情况,不利于精确使用。最后,sympy(数学符号函数库)。在利用Python开展符号运算教学中,应当要加载sympy函数库,其可以让Python转化成代数系统。值得注意的是,微积分符号运算教学中,要提前定义会遇到的全部代数字母。此环节能借助“symbols()”辅助定义数个字母,过程中要关注字母大小写的问题。
二、微积分教学中Python主要运用
(一)函数可视化生成
1.任意指定性质函数
(1)随机函数。随机属于概率学领域的概念之一,随机也是数学讨论的主要方向,同时在密码学中也有涉及。随机数能分成真与伪两类,前者一般是通过物理过程,如量子效应;后者按照特定数学算法形成,自身存在一定规律性,只不过由于循环周期过长,将其视为随机,相关算法有很多,如RAND、线性与非线性同余法[2]。此处利用Python把随机数形成过程以可视化的方式呈现出来,实质上是伪随机数,但在微积分教学下,足够让学生了解随机数。把随机数与函数整合起来,确认x定义域和待生成点的数量(n),设置映射值域,借助Python中random函数便能得到n个通过随机算法形成的yi。定义域选择在[-5,5],而值域是[-2,2],按照点对(xi,yi),便能生成相应的散点图以及折线图。该过程完全是随机的,所有(xi,yi)函数值均为随机赋予,这会令生成图像比较杂乱。在微积分教学中,利用Python可视化生成任意随机函数相应的操作程序为:自建动图、新函数、新增随机函数、任意函数,随后选择定义域与值域,“确定”后返回操作主页面开始“运行”,直接能得出函数图像结果。
(2)连续函数。绘制任意连续函数(y=f(x))图像中,仅需在任意随机函数的基础上,调整y的取值方式即可。按照连续表达如下:

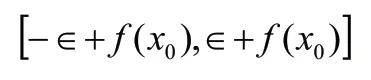
所以随机形成第一个点,之后的函数点便可按照以上方法形成点对。借助Python中的对应函数,能够按照指定区间,形成满足均匀分布的点,继而产生y。微积分教学中,因为计算机既有限制以及Python按点绘线的特征,应当提前设置与,而二者能直接选取较小值,这样能提高绘制曲线的平滑度。
(3)可导函数。针对该类函数的绘制,考虑到Python仅能以离散点作为目标进行绘图,因而实际教学中可运用的绘图程序为:第一步,设置与,两者能对y与x数值间隔进行调整,同时还可以设置定义域。第二步,基于定义域左端,随机选出函数第一个点,即(x1,y1)。第三步,形成第二个点,其横坐标是x2,令x2-x1=,符合领域标准。根据连续性要求,形成f(x2),让前两个点符合连续性。第四步,形成第三个点x3坐标,令x3-x2=,根据可导要求得到f(x3)。第五步,重复上一步操作,借助前两个点得出后面的可导点,直至达到定义域的右端点。通过把微积分内容利用Python进行可视化处理,让学生直接看到可导函数图像,并且在不设置限制条件的情况下,可导函数能形成“趋势”,结果和该函数基本特征一致。
2.微积分重要定义
(1)导数定义。在微积分学科中,导数是极为关键的概念,学生如若要快速使用导数解出问题,应当先明确导数概念与几何意义[3]。为可以动态化显示出其定义,用几何形式呈现,先要在曲线上确认点x0,以此为基础画出切线。在x0周边选出x1点,画出二者对应割线,而后调整x1取值,让其不断靠近x0,将该过程中的割线情况进行动态呈现。这样能够使学生以比较直观的状态,体会从割线变为切线的几何规律,继而形成对导数定义的认识。实践教学演示期间,为便于课上演示操作,教师应当把导数定义直接当成案例保存在资料库内,按照“自建动图”“趣味案例”“导数的几何意义”完成参数设置。随后教师能直接选择现有的函数形式图像与默认第一个点x0,或是自定义函数,在相应定义域中选择x0,“确定”后便能立即获得相应的几何动态演示。
(2)极限定义。在讲解“极限”部分的知识中,为让学生可以清楚地认识道“极限”概念,大多数教师倾向于用“割圆术”为例子展开讲解。相关数学原理为:算出圆形正n边形的面积,视为圆形面积近似值,在n的取值持续加大中,正n边形实际面积也就更接近圆形面积,但不可能相等,这就能体现出“极限”概念。在运用Python进行动态化教学中,也能直接绘制“割圆术”,当作一个趣味案例保存下来。在微积分领域中,“极限”一般是研究函数与数列,考虑到数列理解难度较低,此处选择数列作为分析对象。以下述数列为例,n是横坐标,而数列值是纵坐标,借助基于Python构成的可视化程序,动态呈现数列数值持续接近极限的过程,呈现出“极限”表述内容。

在n持续提高中,函数值始终处于“O”周围,而且持续接近“O”。通过散点图呈现出x轴上点列,并且为了更清楚地反映出“逼近”的情况,把n当成动态变化要素,持续性提高其取值,这样就能呈现出数列“延伸”的状态。
(3)微分定义。对于一元微积分来说,“可微”相当于“可导”,即:

f(x)函数上,随意选择一点L(x0,y0)和其周围一点L'(x0+△x,y0+△y),穿过二者作一条和x轴平行的虚线,基于L点作此切线,并过(x0,0)与(x0+△x,0)分别与x轴虚线及切线相交,用△y表示。因为f’(x)为切线与x轴夹角对应正切值,加之一元微积分特点,所以,函数f(x)在点L的微分,能够用其切线纵坐标的增量代表。运用Python可视化处理工具绘制出函数图像。微分和导数的几何意义图像比较接近,教师也可以直接将其保存在相应案例资料库中,相关操作流程也可参考导数定义的方法。
3.自定义表达式函数
(1)直角坐标函数。在直角坐标函数中,比较多见的形式是y=f(x)。绘制该基础函数图像中,教师仅用确认函数的定义域,假设需要绘制出动态的图像,就应额外设置变化参数[4]。比如,在讲解y=sin(x)中,教师直接选择在基于Python的可视化系统上,进入到“自建动图”模块,点击“新函数”,便能输入所需的函数参数,确认新增与输入表达式函数,设置区域是[-5,5],不设定可变参数。完成上述操作并“确定”后,启动运行就能得到完整的直角坐标函数。
(2)极坐标函数。极坐标方程的基本形式是p=f(θ),鉴于在实际教学中录入“θ”存在一些不便之处,因而改用“r”作为自变量。比如,在绘制从0至2π区间内的阿基米德螺线,此时极坐标方程能用p=r/6代表。教师操作系统中,同样通过“自建动图”模块中的“新函数”,完成相关的参数录入操作。
(3)参数方程。微积分教学中,为便于操作应用,方程参数直接选定“t”,比如在“参数方程画圆”讲解中,参数方程是:
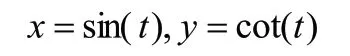
参数t的取值范围为[0,2π]。按照上述操作流程,新建函数即可,通过动态图像观察到的结论,和参数方程基本规律、性质相同。
(二)重要定理可视化
1.连续与极限
(1)介值定理。对于闭区间的连续函数,该定理是其主要性质,其被运用在迭代法求根等类似的“逼近”算法上。为了让学生以比较直接的形式感受介值定理,可视化处理应当是最有效的方法。教学实践中,基于任意闭区间,绘制出连续函数f在其中的图像,同时要确认函数端点数值。在闭区间[f(a),f(b)]内,由ξ动态取遍全部值,但因为绘图形式约束,取值存在间隔,能根据连续定义确认间隔。各个ξ在函数上均有与之相等的点。
(2)零点定理。和上一个定理比较接近,需要先确定合适的“a”与“b”,在[a,b]区间内绘制出f函数图像,让f(a)与f(b)是异号状态。下一步则是使ξ=a,并绘制出此处切线。让后使ξ取遍此闭区间内的全部值,观察该过程中ξ对应切线斜率等于零的情况下,ξ的对应点。
(3)数列极限性质。一方面,有界性,即假设{xn}数列是收敛的,则意味着其一定有界。微积分教学期间,教师可以利用图像呈现出收敛数列性质。以下述震荡数列为例:

该序列极限是3,n是横坐标,而纵坐标是数列值,动态表现出该数列在n数值提高中的变化状态。通过Python绘制,得到的证明结果和收敛序列性质相同。另一方面,单调有界必有极限。针对该准则,此处主要从几何意义角度讨论加以证明。在单调数列({xn})中,数列值仅能基于数轴进行正方向与负方向上的运动,并且只能向一侧移动。假设数列值朝着负方向移动,此时单调数列取值只会出现两种现象,分别是:数列趋于“-∞”;趋于某个固定值。如果单调数列有界,则前者不成立,也就是数列有极限。经过动态图像讲解的方法,发现单调递减数列的数值是无限逼近某个固定值,这意味着此数列的极限就是该值。
2.导数定理
在微积分课程中,关于极限的单元,具体讨论数列与函数极限具备有界性、子列收敛、唯一性、保号性,并包含“夹逼准则”与“单调有界必有极限”[5]。因为定理和性质本身存在明显的特殊性,所以教学讲解证明大多是理论推导,很少会用到图像。但如果在课上教师能够灵活运用Python,实现直观化教学,更容易让学生理解。
(1)罗尔中值定理。其在微积分课程中占据重要定位,通过对其进行动态化处理,可以直接在(a,b)中锁定ξ点,对此应当建立符合相应要求的函数曲线。在连续可导函数(f(x))中,选择[a,b]区间,让f(a)与f(b)相等。在绘制图像中应标记出图像端点,并通过虚线连接。使ξ由a至b移动,显示出ξ对应切线,锁定切线斜率为0的取值,由此可以反映出该中值定理的几何意义。实践教学中,为提高课堂上演示过程的便利性,把此中值定理与其他相关定理都当成教学例子集中保存,相应的调用操作流程和前文关于导数几何意义的处理方式一致。
(2)拉格朗日。此项中值定理描述了在闭区间中,可导函数的导数改变与其端点割线斜率的联系。在讲解其几何以一种,同样要先绘制出原始函数图像,设置端点。使ξ由a至b完成取值,绘制相应切线,在此期间确认其和割线相互平行的点。通过运用Python绘制动态图的方式,将中值定理呈现出来,使学生可以直观理解定理描述的关系。
3.积分定理
(1)不等式。微积分课程的众多不等式中,积分不等式属于比较重要的抑制,其是解出微分方程的重要工具,具体有闽可夫斯基与杨不等式等。例如,在讲解杨不等式中,对其进行几何意义分析。教师先要绘制函数图像,区间为[0,a],标出端点与对应虚线。在纵坐标轴上选择一点b,使其动态移动。由此形成两个多边形,在b不等于f(a)的情况下,两个多边形的面积和大于ab。
(2)积分中值定理。其包含一重积分与二重积分两种,前者还能细分成积分第一与第二中值定理。以积分第一中值定理为例,这是由于其在实质上和二重积分中值定理比较接近,所以,更具分析代表性。该定理的基本描述为:假设在[a,b]区间上,f(x)函数是连续的,则在该区间中至少有一点ε符合以下条件:

在函数定义域内,等于曲线和x轴构成一个面积,则在积分第一中值定理对应几何意义为:定义域作为图形的底,曲线上某个点是高,由此形成的矩形面积就是曲线积分值。而该几何分析过程能根据介值定理得出。相应的分析推导思路为:假设在[a,b]区间上,函数最大值是M,最小值是N,在以二者为高形成的矩形面积中,会存在下述结果:

按照介值定理,便能确认在此区间中,函数上至少有一点ε符合要求。
三、结束语
微积分知识本身的理解难度较大,而且各类定理、定义较多,倘若仅依靠理论推导,可能容易导致学生理解偏差以及混淆等问题出现。而借助Python绘图功能,可以按照设定条件直接生成函数图像,并支持动态演化,这样有利于学生掌握定理描述本质,灵活运用解出数学问题。

