让推理意识无痕发展
杨慧
【摘 要】发展学生的核心素养,是当前数学教学的重要目标。教学“三角形按角分类”时,教师引导学生充分经历概念产生、完善以及概念体系形成的过程,使学生在深刻理解数学知识的同时,获得推理意识的锤炼,实现核心素养的提升。
【关键词】三角形分类;数学概念;推理意识
《三角形的分类》是人教版教材四年级下册的教学内容,旨在让学生通过操作、观察、比较、归类等活动,经历给三角形分类的过程,辨认和识别锐角三角形、直角三角形和钝角三角形,知道这些三角形的特点。其中,既包含图形认识和概念建构的双基目标,又蕴含发展空间观念的能力目标。分类是一种科学的思维方法,根据分类标准的不同,通常可以分为基于形式的分类与基于性质的分类。三角形按角分类,是基于显性的外在形式的分类。本课的教学在学生初步掌握三角形内角和是180度的基础上,关注如何在分类过程中,引导学生理解三角形的内在本质。
【教学目标】
(1)通过动手操作,经历给三角形分类的过程,辨认和识别锐角三角形、直角三角形和钝角三角形,知道这些三角形的特点。
(2)通过观察、画图、计算等活动,培养空间观念和归纳推理能力。
(3)通过比较、归类等活动,渗透分类思想和集合思想。
【课堂实践】
一、分类交流,建构概念
理解三角形按角分类的分类结果不难,学生预学后就能大致明白。教学时,教师在学生暴露自身“原始概念”的基础上,呈现教材上的“标准概念”,以此引发学生的认知冲突,让学生通过思考和分析,理解如此分类的原因,并建构相关的概念,在感受数学语言严谨性的同时,锤炼推理意识。
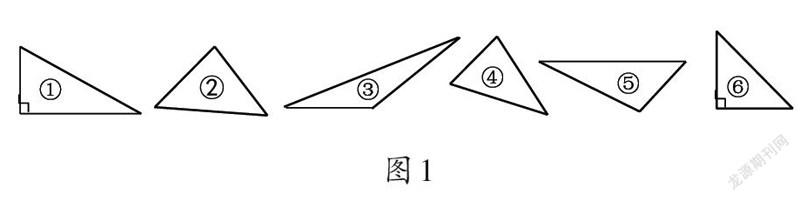
师:同学们,今天我们一起来研究三角形的分类,研究的内容是按角分。昨天我们进行了预学,有关知识想必大家已经知道了不少。现在黑板上有六个三角形(如图1),哪位小老师能上台来分一分、讲一讲?
生:图①和图⑥是直角三角形,因为它们都有一个直角两个锐角;图③和图⑤是钝角三角形,因为它们都有一个钝角两个锐角;图②和图④是锐角三角形,因为它们的三个角都是锐角。
(其他学生都表示同意)
师:这名同学在表达的时候,既能说出结果,又能说出理由,非常棒。我现在把他说的写在黑板上。(结合学生的分类,板书简要记录)
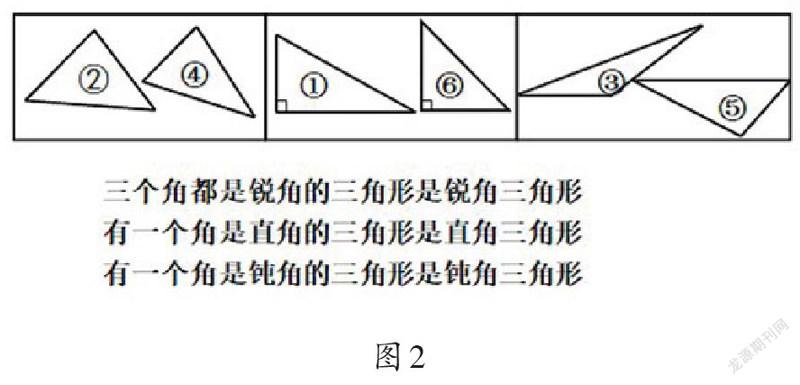
师:我們来看看课本上是怎么描述这三类三角形的。(课件出示图2)仔细观察并比较,课本上说的和刚刚这个同学说的有什么不同?
生:课本中锐角三角形的描述和同学说的一样,但钝角三角形和直角三角形,课本上只说了其中的一个角,没有说两个锐角。
师:你们一定产生疑惑了吧。课本在直角三角形和钝角三角形的概念中,为什么不说明它们都“有两个锐角”?(学生安静思考)
生:三角形的内角和是180°,直角是90°,那么直角三角形中另外两个角的和也是90°,所以直角三角形中另外那两个角肯定都是锐角。同样,钝角是大于90°的,三角形中如果有一个钝角,那么另外两个角的和就会小于90°,它们只能是锐角。既然都一定是锐角,也就不需要再特地说明了。
(学生清晰的表达,得到了同学们热烈的掌声)
师:这名同学通过推理,分析了原因。同学们,数学表达就是要既严谨又简洁。
二、质疑问难,说理求证
在学生知道了锐角三角形、直角三角形和钝角三角形的概念后,教师适时抛出“有没有第四类三角形存在”这个问题,引导学生通过不同的方法来证明“三角形只有三类”这个结论的正确性。这个说理的过程,是学生数学思维不断调整、完善的过程,也是其推理意识不断增强、发展的过程。
师:我们把三角形分成锐角三角形、直角三角形和钝角三角形三类,那么有没有第四类三角形呢?
生:没有了。
师:能用充分的理由来说明自己的观点吗?可以想一想,画一画,说一说。(组织同桌讨论)
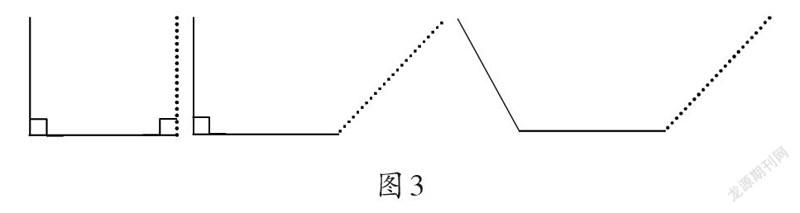
生:老师,我到黑板上来画一画。如果三条线段组成两个直角,是不可能围成一个三角形的;组成一个直角、一个钝角也不行;组成两个钝角就更不可能围成三角形了。因此只有这三种情况(如图3)。
师:画图是个好方法,它让大家非常直观地理解你的观点。
生:我们也可以通过计算来证明,三角形内角和是180°。如果三个角中有两个角是直角,那第三个角就是0°了;如果有一个直角和一个钝角,那第三个角就是负数了……
师:你是通过计算进行推理的,也非常不错!所以,三角形按角分的确只有三种情况,我们可以用这样的集合图来表示。(课件出示图4)
三、利用“负迁移”,引发新思考
教师利用学生思维的“负迁移”——有一个锐角的三角形叫锐角三角形,引导学生对三角形的角(尤其是锐角)展开更深入的思考。学生通过对三类三角形中各个角的对比分析和归纳,得出“三角形中至少有两个锐角”,进而形成确定三角形的类型“要看两个锐角外第三个角”的经验。在这个过程中,学生发展了理性的思维方式。
师:现在我们知道了有一个直角的三角形叫什么?
生(齐答):直角三角形。
师:有一个钝角的三角形叫什么?
生(齐答):钝角三角形。
师:有一个锐角的三角形叫什么?
生(齐答):锐角三角形。
(教师有意停顿,很多学生突然发现答案不对,纷纷举起了手)
师:怎么了,出什么问题了吗?
生:因为任意三角形中都有锐角,所以有一个锐角不能确定是什么三角形,有三个锐角才能确定是锐角三角形。
师:这样啊!请大家观察板书,并比较,你们有什么新的发现吗?
(教师组织学生观察、讨论和交流)
生:每种三角形都至少有两个锐角,判断三角形时,光看两个锐角还不够,还要看第三个角,两个锐角外的第三个是什么角就是什么三角形。
(教师根据学生的回答,通过板书引导学生更清晰地理解分类标准)
师:现在,谁能完整地说说我们的发现。
生:每种三角形至少有两个锐角,所以要再看第三个角。第三个角是锐角的就是锐角三角形,第三个角是直角的就是直角三角形,第三个角是钝角的就是钝角三角形。
四、利用几何画板,掌握新判断方法
从“需要知道三个角的度数”到“只需要知道一个角的度数”,再到“关键要看最大角的度数”,这是学生深刻理解三角形本质、提升思维能力的过程。教师以几何画板为载体,引导学生观察、想象、分析,直观地感知三个角的内在关联,使学生的推理意识和空间观念得到同步发展。
师:要判断这是一个什么三角形,需要知道几个角的度数?(课件出示图5)
生(齐呼):三个。
(有学生大喊“看一个也行”)
师:有人说看一个角也行,这有什么道理吗?
生:在这个三角形中,∠S最大,有点像直角,也有点像锐角,所以只要确定∠S就可以了。
师:好,现在我们来测量一下∠S的度数。(课件显示∠S=87°)它是什么三角形?
生(齐答):锐角三角形。
师:为什么?
生:因为这个角最大,而且是锐角,那另外两个角一定也是锐角,所以它是锐角三角形。
师:想象一下,如果现在向右拖动S点,这个角会发生什么变化?
生:∠S会变小。
师:我们来试一下,看看是不是这样。
(课件动态演示过程,结果如图6)
师:现在是什么三角形?
生:钝角三角形。
师:∠S明明只有19°了,这个三角形怎么会是钝角三角形呢?
生:因为∠R变成钝角了。
(课件分别显示∠Q、∠R的度數,其中∠R为101°)
师:现在关于如何判断一个三角形的类别,你们有什么新的想法?
生:关键要看三角形中最大的那个角。如果最大的角是直角,它就是直角三角形;如果最大的角是钝角,它就是钝角三角形;如果最大的角是锐角,它就是锐角三角形。
【教学反思】
本设计的主要特点如下。
(1)当学生按角对三角形进行分类时,教师设计了“有没有第四类三角形存在”这个问题,让学生用画图、计算等不同的方法来说明思考过程,引导学生理解概念本质,感悟分类思想。
(2)学生在分类过程中,往往关注每类三角形的独特之处,而忽视它们的共性部分。针对这一现象,教师设计了找一找“直角三角形的另外两个角”“钝角三角形的另外两个角”等练习,让学生既对直观的现象进行观察与归纳,又根据三角形的内角和来分析和解释。
(3)发展学生的空间观念,离不开动态想象。教师在学生对三角形进行静态探究时,运用几何画板,展示三角形的动态变化过程,让“推理”和“验证”结合,清晰呈现学生思维的发展变化。
教学时,教师引导学生经历数学问题的分析和解决过程,培养学生的推理意识。本课围绕四个主题设计教学。前两个主题是:“直角三角形和钝角三角形的另外两个角一定是锐角吗?”与“除了这三类,还存在第四类三角形吗?”这两个主题的解决,其实都用到了推理。教师通过提问,引导学生进行观察、分析、讨论,学生会主动地利用“三角形内角和等于180°”进行思考和说理。学生的说理过程实际上就是推理过程,在这个过程中,学生既解决了问题,又感受了数学的严谨性。第三个主题是:“一个三角形中至少有几个锐角?”看似简单的一个问题恰恰是本节课的难点。通过观察、比较,学生感悟到三角形的分类由第三个角来确定,他们理解问题的方式也从直观感知发展为抽象推理。第四个主题是:“判断三角形的类型需要知道哪些角的度数?”从需要知道三个角到只需知道一个角,从看特殊角到看最大角,在教师的不断追问下,学生的思考不断深入,最终实现概念理解。在以上解决问题的过程中,通过多种方法的碰撞、多样思维的分享,学生的推理意识在无形中得到发展。
在小学数学教学中,教师要特别注意挖掘数学知识点之间的逻辑关系,在此基础上,精心设计教学的过程和形式,有意识地培养学生的推理意识,促进学生数学素养的有效提升。
参考文献:
[1]顾文亚,严育洪.关注思维,向更深处漫溯:“三角形的分类”课堂实录与评析[J].中小学数学(小学版),2021(7/8).
[2]董连春,陈洪杰.国际小学数学教与学的研究进展与启示:基于ICME-14全体报告和邀请报告的述评[J].小学数学教师,2021(9).
[3]刘伟.浅谈通过问题设计培养学生的逻辑推理意识[J].试题与研究,2022(22).
(浙江省舟山市普陀区教研室 316100)

