经历探究过程建立数学模型
——《植树问题》教学设计与意图
文|朱 欢
【教学内容】
人教版五年级上册第106、107 页及相关练习。
【教学过程】
一、创设情境,引入新课
师:生活中处处有数学,伸出你们的一只手,张开手指,用数学的眼光观察一下,你看到数字几?
生:数字5。
师:5 个?
生:手指。
师:除了看到数字5,还看到了数字几?
生:数字4。
师:4 个?
生:4 个手指缝。
师:手指缝,在数学上我们可以把它叫作间隔。那么,5 个手指之间有几个间隔?4 个手指之间有几个间隔呢?3 个手指呢?2 个手指呢?
生:4 个、3 个、2 个、1 个。
师:通过刚刚的学习过程,你有什么发现?生:间隔数比手指数少1。
师:在数学上,我们把这种和间隔数有关的问题,统称为植树问题。(板书课题:植树问题)
二、自主探究,构建模型
1.出示问题,引出三种不同的情况。
课件出示:同学们要在全长100 米的小路一边植树,每隔5 米栽一棵,一共要栽多少棵树?
师:请看大屏幕。自己读一读,说一说找到了哪些有用的数学信息?要解决的问题是什么?
生1:小路长100 米,每隔5米栽一棵树。
生2:是在小路的一边植树。
生3:要解决的问题是“一共要栽多少棵树”。
师:“一边植树”是什么意思?
生:小路有两边,我们只要在一边植树就可以了。
师:“每隔5 米栽一棵”,你们是怎么理解的?
生1:栽一棵树,隔5 米再栽一棵树。
生2:两棵树之间的距离是5米。
师:同学们理解得真到位。猜一猜,100 米的小路一边植树,每隔5 米栽一棵,一共要栽多少棵树?

生:20 棵、21 棵、19 棵。
师:有三种不同的答案,怎么办?
生:动手画一画。
师:好主意。接下来,请同学们在草稿纸上画一画,看看到底能栽几棵树?
师:照这样一棵一棵地画下去,感觉怎么样?
生:太麻烦了。
师:是啊!一节课的时间有限,这么长的路我们可不可以——
生:取其中的一部分。
师:取多长为好呢?
生:10 米、20 米、30 米……
师:10 米太短了,30 米又有点长,那就选20 米吧。像这样从简单的情况入手,在数学上叫作“化繁为简”。(板书:化繁为简)
课件出示:在20 米的小路一边植树,每隔5 米栽一棵,一共要栽多少棵树?
师:同学们能不能试着在纸上画一画或是算一算,然后再与你的同桌说一说。
教师巡视,适时参与学生的讨论与交流,选择三位同学的作品展示在黑板上。


师:仔细观察这三位同学的作品,它们有什么相同的地方?
生1:他们都是每隔5 米栽一棵树。
生2:都是4 个间隔。
师:你们知道这4 个间隔是怎么算出来的吗?
生:20÷5=4(个)。
[板书:20÷5=4(个)]
师:20 表示?5 是?4 是?
生:20 表示小路长20 米,5表示每5 米栽一棵,4 表示4 个间隔。
师:刚才我们比较了相同的地方,现在我们来比较不同的地方。
生1:第一位同学种了5 棵树,第二位同学种了4 棵树,第三位同学种了3 棵树。(板书:5 棵、4棵、3 棵)
生2:第一位学生两头都种了树,第二位同学只在一端种了树,第三位同学两端都没种。
师:为什么第二位同学只在一端种了树,第三位同学两端都没种呢?他们可能遇到了什么情况?
生:可能有房子或障碍物。
师:是的,当一端或两端有房子的时候,还能种下树吗?
生:不能。
师:我们能不能给这三位同学种树的情况想一个名字?
生:第一位学生两端都栽,第二位同学只栽一端,第三位同学两端不栽。(板书:两端都栽、只栽一端、两端不栽)
2.发现棵树与间隔数的规律。
师:4 个间隔5 棵树、4 个间隔4 棵树、4 个间隔3 棵树,棵树与间隔数如此的接近,看来棵树和间隔数之间一定有联系,你能找出来吗?
生:两端都栽的情况:棵树=间隔数+1;只栽一端的情况:棵树=间隔数;两端不栽的情况:棵树=间隔数-1。(板书)
师:除了看数字之间的关系,还可以从哪里看出来?
生:从图中看出来。
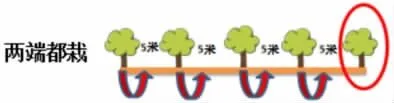
师:一棵树对应一个间隔,在数学上叫作:一一对应。(板书:一一对应)下面我们就用一一对应的方法来看一看其他的两种情况。


师:好了,现在咱们回到开始要解决的问题:要在全长100 米的小路一边植树,每隔5 米栽一棵,一共要栽多少棵树?同学们说一说:栽21 棵是怎么来的?
生:先 求 间 隔:100÷5=20(个),再用20+1=21(棵)。
师:这是属于植树问题的哪种情况?
生:两端都栽的情况。
师:那你们知道20 棵和19棵分别属于植树问题的哪种情况吗?
生:只栽一端和两端不栽的情况。
三、分层练习,形成能力
1.基础题。
(1)工人们正在架设电线杆,相邻两根间的距离是200m。在总长为1000m 的笔直路上,一共要架设多少根电线杆(两端都架设)?
(2)迷你马拉松比赛全程约12km,平均每3km 设置一处饮水服务点(起点不设,终点设),全程一共有多少处这样的服务点?
(3)一根木头长8m,每2m 锯一段,需要锯几次?
2.拓展题。
找一找生活中类似植树问题的情况。
3.拔高题。
四、课堂小结,拓展延伸
师:说一说,这节课你有什么收获?

