行进四理，沉淀可见的数学核心素养

文 陈 静 方学法

数学核心素养指向学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。在小学数学课堂教学中，笔者通过引导学生带着问题意识思考联系、实践探析、明晓道理、融通算理，于“思——探——明——融”的思维行进中落实学生数学核心素养的培养。

一、思理：在关联中感悟，促进数学抽象

1.情境体悟中明晰数学源起。

创设与学生生活场景相符的数学情境，让学生用数学的眼光观察现实世界并抽象出数学思考，以及带着数学思考走入数学探究，通过情境体悟数学是生活常识与数学知识连接转化的路径。

《小数的意义》课堂开始，教师就将学生的视野引出课堂、引入生活，在关注学生已有经验中打开学生发现生活中数学知识的眼界，引导他们主动提取知识储备中与小数知识点关联的情境。

师：生活中，你在哪些地方见过小数的身影？

生1：我和妈妈去买菜,看到菜场里大白菜一斤1.5 元。

生2：水果店苹果一斤3.9 元。

生3：玩具店小汽车一个19.9 元。

生4：超市里可乐一瓶5.50 元。

生5：我数学考试得了87.5 分，体温是36.5 摄氏度，身高是1.56 米。

师：这些生活里的小数都是如何利用数学规定得到的呢？咱们一起走入“小数意义”的研究。

在对小数意义的探索中，学生发现现实生活中的小数其各相邻数位之间的进率在整数、小数之间有浑然一体的统一：相邻计数单位间的进率都是10。进率和数位的解读为学生后续“由现实生活中抽取出小数加减法的算理”做了意识方面的铺垫。学生在浸入情境、抽取数学、思考数理的过程中，体悟到了数学的抽象性———“数学就是生活的再现”“生活的提取与提炼最终抽象出了数学”，培养了学生从现实世界中抽取数学信息以及从学科的角度观察现实世界、明晰学科特征的能力。

2.方法优化中生发数学意识。

择选最优化算法的能力是学生应用意识乃至创新意识在学习中的体现，是指学生在自主探究、倾听思考、互动分享中从多样化的策略里选择最佳方法的能力。

苏教版一年级下册《整十数加减法》的教学中，当教师追问40+30 等于多少时，学生根据在100 以内数的认识中积累的原初思维“4 个十加3 个十得7 个十”，算得结果是70。基于此,教师引导追问：7 个十的7 就是几与几合起来的结果？3、4、7 分别代表什么意思？学生在教师的追问和自己的讨论中，思维水平由呈现4 捆小棒、3 捆小棒到4 份、3份再到抽象出数字4、3，这一过程是学生思维由感性具体到感性一般再到数学简约的进阶，学生由4+3=7 思考40+30=70，是其数学思维方法的优选、数学意识的培养。

二、探理：在思辨中迁移，促进数学推理

1.沟通比较中厘清知识本质。

小学数学教材编排以数学知识的发生、发展、运用为主线，数学知识中所蕴含的学生不易察觉的数学思想，需要教师从数学发展的全局着眼，从具体的教学过程着手，引领学生沟通比较、探索新旧知识联系，厘清知识本质。

苏教版六年级上册《探究规律——数形结合的策略》的教学，是在学生学习《分数四则混合运算》单元后的一堂综合实践课，对其知识本质联系，教师是如下呈现推进的：

旧知唤醒：

一个长6 厘米、宽4 厘米的长方形，长扩大2 倍，宽扩大2 倍，现在的面积是原来的（ ）。

一个长6 厘米、宽4 厘米的长方形，长扩大2 倍，宽扩大3 倍，现在的面积是原来的（ ）。

迁移探索：

学生通过迁移“整数倍变化”自主探究“分数倍变化”，在变中找不变（探究方法不变），不变中找变（倍数不变图形有变），学生在关乎知识本质的探索中意识到了数学规律的普适性，培养了他们运用已有知识和经验解决问题的能力和在练习中学会反思推理的能力。

2.鼓励质疑中培养批判思维。

小学生年龄的特点决定了他们有较强的向师性，一般信服老师的话语，较少批判质疑，有的老师也愿意采取自己说方法、自己说结果的方式教学，学生的“自己发现和提出问题”“ 独立思考、学会思考”的能力薄弱，更无法通过推算梳理来解决自己遇到的数学问题。

苏教版《和与积的奇偶性》一课中，当学生通过有序列举发现和的奇偶性与加数的奇偶性有关——加数中有奇数个奇数时，和是奇数；加数中有偶数个奇数时，和是偶数。有学生进一步解读道：我知道为什么加数中有奇数个奇数，和是奇数。因为每个奇数都可以分成偶数加1 的形式，偶数个奇数带来偶数个1，每两个1 都可以组合成偶数，余下一个奇数带来的1落单了，所以奇数个奇数相加和是奇数。大多数学生表示理解并赞同该同学的解读，但另一同学举手质疑道：老师，我想知道这个落单的1 是哪个奇数里的1？教师没有急于回答，而是将这个问题抛给了所有同学，有同学说是最后一个奇数里的，有同学说是第1个奇数里的，有同学说是中间奇数里的。教师追问：最终影响和成为奇数的那个1，跟在哪个奇数加数中有关吗？

在“理越辩越明”中学生拨开了思维混乱的迷雾，开拓了思路，提高了批判思维和推理能力。

三、明理：在深挖中理解，促进数学建模

1.分层学习中查明结构聚合。

数学课程要面向全体，使不同的学生在数学上得到不同的发展。教学时应给每个学生创造“跳一跳摘到桃子”的机会，并在各自任务分享中获得思维的提升与进阶。

苏教版《平面图形的面积整理与复习》中，“你们都认识哪些平面图形？”“能一边介绍特征一边在白板上画出来吗？”“谁愿意来回忆、整理一下这些平面图形的面积？”“这6 类平面图形的面积推导过程，存在着怎样的联系呢？”不同的学生在问题追问深入的路上，经历不同的层级任务，最终完成散点思维至整体思维的架构，经过层层深入复习，学生平面图形的知识结构由特征扩展至计量，面积计算由简单延伸至复杂——准确把握特征才能准确切入完成计量；长方形面积计算是学习其他图形面积计算的基础。反过来，每一种新的图形面积计算都是建立在原有图形基础上的。

2.习题组块中找准问题模型。

数学教学多是以建构主义理论为依托，注重对学生已有知识经验和生活经验的挖掘，“习题组块”能为学生搭建自主探究的阶梯，在引导学生经历分析、抽取、建模、验证概括的基础上培养其模型意识和数据意识，并借此提升其核心素养。

苏教版《分数的意义》一课，教师在引领学生理解意义、刻画生活、体会价值、感受联系的基础上设计分层习题，学生在异中求同、同中求异、质疑问难中积极思考、主动探索，在辨析交流中体会和理解了分数与外部世界的联系，聚焦分数意义概念的本质（如图1）。

图1 分数的意义

学生在习题组的思维辨析中，理解感悟、探究异同，经历从具象事物中抽象出数学问题、提取具体信息中的数学符号、解读数学符号代表的数学信息、将数学信息的内涵推衍至同类别问题这一过程。学生在这一过程中，发展了数学思考能力和问题解决能力,并建立了关于分数特征的知识模型，积累了基本的数学思想和活动经验。

四、融理：在体系中丰盈，促进数学应用

1.思维导图中融合知识框架。

学生形成性知识框架的文图呈现，是教师教学内容和学生学习过程的总结提炼。课堂上，师生互动、小组分享、个体质疑、群体释疑……都涌动着知识的痕迹，学生课后将“痕迹”及由痕迹带来的思考用思维导图的方式梳理出来，无形的痕迹经由笔端有形地呈现出来，具化了学生的知识框架，动手绘制的过程就是把握知识点实质和知识点间关联的过程。

如复习同一平面内两条直线的位置关系时，学生绘制了下图（如图2）：

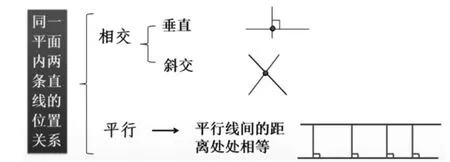
图2 同一平面内两条直线的位置关系

思维导图的使用有利于培养学生有序思维、反思重建、融通知识的能力，学生将所学、所思、所悟融入框架体系，在思维输出中构建了知识体系。

2.开放脑域中激发创新思维。

小学数学教学中研究的绝大多数生活题都是指向唯一思考策略与答案的，但实际生活情境中会遇到“综合考量”“联系实际”的情况，这就要求教师引导学生通过“讲数学话”而“思生活事”，将数学与生活相融合，以进一步发展学生的问题解决能力。

在苏教版六年级总复习时，出现过这样一道题：在一条2700 米公路的两头，有两个新建小区，分别入住360 户和720 户居民，要在它们之间的某个位置新建一个超市，你认为建在哪里比较合适？有的学生认为该修在2700÷2=1350（米）处，因为虽然存在户数多少之别，但户数少的小区可能是多层，房价高，居民消费能力也较高，超市建在两个小区的正中位置，不会影响超市的销售额；有的学生认为应该根据入住居民户数比的反比确定超市位置，户数多的小区会带来超市更高的销售额，所以要将超市建得距离该小区更近一些；有的学生则觉得不能简单地只通过“数学信息”和“可能猜测”来完成新建超市的选址，建议通过设置一份囊括“家庭人数、人员分类、家庭年收入、采购喜好”等类别的问卷，通过详细分析问卷，得出两个小区购买能力的强弱对比，再确定新建超市的选址……

学生最终的答案并不唯一，不同的学生呈现出不同的思考策略，不同的思考策略指向不同的结果呈现，学生“数学应用意识”越强，其“生活化”的思维能力就越强，考量问题就越全面。教师在肯定中引导学生经历思考的过程、感受问题解决的方法、理解优化问题方案的必要，潜移默化中培养了学生的应用意识。

数学是智慧的学科，我们只有带领学生不断地多角度思考、多方式拓展，且思且探，陪伴学生在“是什么”中思理，在“为什么”中探理，在“在哪里”中明理，在“怎么做”中融理，才能使学生明晰知识脉络，让学生在生活中学会用“数学的眼光”“数学的思维”“数学的语言”分析问题，培养学科核心素养。