在不断度量的过程中学习面积
——《认识面积》教学设计
文|成艳斌 李 霞
【教学内容】
苏教版三年级下册第58~60页。
【教学过程】
一、链接生活,唤醒经验
1.直观比较,面有大小。
师:这是老师的新家(同时出示房间图片),为营造幽静的读书氛围,我特意为书房铺了木地板;而客厅和卧室呢,为了让房间通透明亮,都铺上了同一款乳白色的地砖(如下图)。打扫新家时,我的儿子和他的爸爸负责拖客厅和卧室的地面,如果是你,会怎么选择?说明理由。

生:我是小孩儿,选卧室地面,因为卧室地面比较小。
生:我选客厅,因为客厅地面比较大,爸爸工作比较辛苦,我想帮爸爸多干一些家务。
(教师板书“地面大小”,并相机对学生进行“爱劳动、有孝心”的教育)
2.以小量大,初识“面积”。
(1)用数描述。
师:那客厅、卧室的地面到底有多大呢?你能用一个具体的数来描述吗?
生:(数一数后)客厅地面有30 块地砖那么大,卧室地面有20块地砖的大小。
师:(如图)书房地面铺的是木地板,你能描述书房地面的大小吗?

生:书房地面大约有14 块木地板的大小。
生:每一行都有一块不完整的木地板,把两个半块儿拼起来近似完整的一块,所以我认为书房地面大约有15 块木地板的大小。
师:这种拼起来的想法很好,化零为整的结果更接近书房地面的准确大小。
(2)变换情境。
师:生活中除了地面,还有很多面,窗户面、墙面、柜面……你能描述这些面的大小吗?
生:一个落地窗有3 块玻璃的大小。
生:背景墙有8 块墙板的大小。
(3)引出概念。
师:通过刚才的学习,我们知道了面有大有小,它的大小还能用一个具体的数描述出来,这就是我们今天学习的新内容——“面积”。如用30 块地砖能正好铺满客厅地面,就可以说客厅地面的面积是30 块地砖的大小;大约用15 块木地板正好铺满书房地面,就可以说书房地面的面积大约是15 块木地板的大小……
师:同桌互相说一说柜面、墙面的面积有多大?
二、动手操作,探究新知
1.设置冲突,提出问题。
师:刚才我们描述了那么多面的面积,那课桌面呢?你能描述它的面积吗?
生:不能,桌面上什么也没有摆。
生:可以,(学生边说边比划)用文具盒(底面)就能量出来。
师:和地面、墙面相比,课桌面上确实没有小格子,这是个问题。但有些同学已经开始自选单位进行测量了,真好!
2.自选单位,完成度量。
(1)明确要求,小组活动。
四人小组为单位,先商量用什么面去量桌面的面积,可以自选,也可以用老师提供的正方形、三角形,选择不同的素材多量几次,将结果记录在《活动单》上。
(学生活动,教师巡视,收集作品)
(2)分类呈现,集体反馈。
①满铺法。
生:用数学书封面量,课桌面的面积比4 本数学书封面大一些。
生:用正方形量,课桌面的面积大约是24 个正方形的大小。
生:用圆量,课桌面的面积大约是24 个圆的大小。
②半铺法。
生:用三角形摆,(边说边比划)横着一行摆11 个,竖着可以摆4 行,用11 乘4 等于44,所以课桌面的面积大约是44 个三角形的大小。
生:用正方形摆,我觉得也不需要摆满,只摆一行一列就行。(边说边指)每行摆6 个正方形,能摆4 行,用6 乘4 等于24,所以课桌面的面积大约是24 个正方形的大小。
师:像刚才这两位同学的方法,只摆一行一列,没有铺满桌面,真的能测量出课桌面的面积?
(同桌交流,再集体汇报,尽可能达成方法优化的共识)(3)比较异同,总结方法。①寻找测量通法。
师:在刚才的活动中,同学们用自己选择的标准,用自己喜欢的方法,进行测量,并且用一个数具体描述了课桌面的面积,真了不起。对比这些方法,有什么相同之处呢?
生:都是用比课桌面更小的面来测量的,都能表示出课桌面的面积。
师:同一个课桌面,为什么我们得到的结果不一样呢?
生:因为选择的度量标准不同。
小结:像刚才测量课桌面的面积一样,测量一个面的面积,通常先选一个较小的面作标准,数学书、笔袋、练习本、手掌面等就是我们选择的标准,然后再数一数有多少个这样的标准,就知道了它的面积。
教师板书:以小面量大面、定标准(单位)、数个数(结果)。
②优化测量标准。
师:这些标准中,你觉得哪一个标准最好?
生:我选数学书(封面),因为它比较大,量的时候很省劲儿。
生:我选正方形,因为桌子都是有角的,正方形也有角,这样量起来方便。
师:那圆形和三角形呢?
生:圆形有弧度,拼起来的时候四个圆中间会有空隙,得到的结果不准确,三角形也会出现同样的情况。
师:是的,在测量过程中,单位应该密铺,由此看来,正方形能够将课桌面尽可能地铺满,不留空隙,是个好单位。
3.面有分类,完善认知。
师:我们刚才测量了像地面、墙面、桌面等物体表面上平平的面的面积,请大家思考,物体表面上有没有不平的面,不平的面有面积吗?
(学生先小组讨论,再集体反馈)
生:篮球的面就是弯曲的,把一个篮球划破,展开,那块胶皮(的大小)就表示它的面积。
生:薯片桶旁边的面(侧面)也是弯曲的,可以找一张能正好包裹住桶(侧面)的纸,然后再用小格子量出这张纸的面积。
师:你们用把曲面展开成平面进行测量的方法,证明了曲面也有面积。
小结:物体表面有平面,也有曲面,它们的形状不同,在物体表面的位置也不同,但这并不影响我们能测量出这些面的大小,也就是它们的面积。
三、拓展延伸,深化认识
1.封闭图形才有面积。
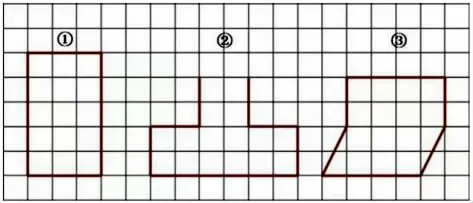
师:你能说出下面图形的面积是多少吗?比一比,哪个图形的面积最大呢?
2.区分“周长”和“面积”。
(1)自主尝试,暴露学情。
教师呈现修正后的图形(如下图),学生独立思考,再集体反馈。
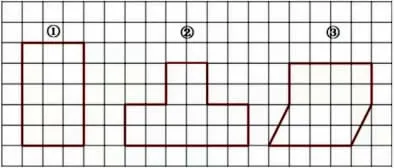
生:①号图形里面的小方格有3 列5 行,所以1 号图形的面积是15 格。②号图形不规则,可以一格一格地数,它的面积是16 格。
生:也可以把②号图形分成四个大正方形,每个大正方形里有4 格,4 乘4 等于16 格。③号图形也一样,把左边多出的三角形移到右边,就拼成了一个大正方形,面积是16 格。
生:对,①号图形面积最小,②号和③号图形的面积相等。
师:①号图形是长方形,我们可以直接数或计算,②号和③号图形,本来是不规则的图形,分一分、移一移,就变成了规则图形。
(2)深入思考,突破难点。
教师用课件动态演示③号图形平移变换的过程,引导学生仔细观察:什么变了,什么没变,并说明理由。
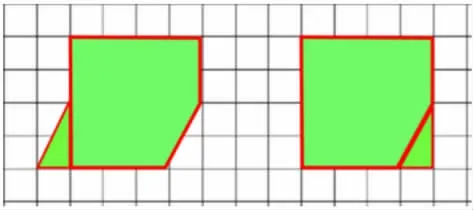
(学生小组讨论后集体反馈)
生:我发现形状变了,周长也变了,(该学生先描出了两幅图对应相等的边线,然后又描出了两幅图对应不等的边线)斜着的这条线比竖着的这条线长(也就是三角形的斜边长大于直角边),所以周长变小了,但是面积没变。
师:看来,周在面的边沿,而面在周的内部。面积就是物体表面或封闭图形的大小,用包含有多少个方格来刻画。
3.以“度量”为主题梳理知识脉络。
教师用课件逐个呈现“量的计量”的学习内容。
师:在以前的学习中,我们测过线的长短,6 个1 厘米就是6 厘米;量过物体的轻重,7 个1 千克就是7 千克;还测过时间,2 个1小时就是2 小时……同学们,对比长度、质量、时间……和今天学习的面积,有什么相同和不同之处呢?
生:每个数的后面都有一个单位,单位不一样。
生:有几个单位,它的结果就是几。
小结:度量的一般过程就是根据度量对象,先定标准,再数个数。有几个这样的单位,结果就是几;度量对象不同,单位也不同。我们今天学习的是面积,度量的对象是面,它有大有小,它的大小是用小面的个数来刻画的。
四、回顾总结,深化认识
师:回想这节课的学习,你有哪些收获?

