海底电缆转换波数据处理关键技术及在南海某区的应用

张兴岩,张立霞,方中于,张 敏,丑纪辉

(中海油服物探事业部 特普公司，广东 湛江 524057)

1 引 言

除了构造勘探.多波多分量地震勘探还可以进行岩性识别、气云区成像、储层预测、裂缝检测、含气性识别及流体性质判别等，能有效降低单分量地震勘探的多解性，提高复杂岩性油气藏预测精度[1]。 近年来，海底地震勘探(Ocean Bottom Seismic,OBS)这种宽方位角多分量采集在海洋地震勘探中逐渐得到了广泛的应用[2,3]，使得海洋地震勘探具备了转换波勘探的资料基础。但是由于当前处理技术的制约，目前国内大部分OBS资料生产时只使用了P、Z两个纵波分量，X、Y两个转换波分量没有处理，这就使得转换波分量中的地震信息没有得到应用，降低了OBS勘探的性价比。此外，相对于纵波，转换波信噪比一般较低，同时由于传播路径具有不对称性[4]，其对各向异性更敏感，所以常规纵波处理技术不适用转换波地震资料处理[5]。近年来，地球物理学家一直在研究[6-13]，Li等[7]、Dai等[8]基于双平方根方程推导了VTI(Vertical Transverse Isotropy, VTI)介质中转换波非双曲线时距曲线方程，奠定了转换波各向异性成像的理论基础；Lüth等[9]根据转换波传播路径的特点，依据共转换点CCP(Common Conversion Point,CCP)对称偏移孔径保证了偏移孔径的优化选取。陈阳阳等[10]通过角度扫描法计算出了地震转换波在地层界面处的转换点位置。岳玉波等[6]就VTI介质转换波Kirchoff叠前时间偏移实现过程中的几个关键技术环节进行研究分析，并给出了相应的实施方案。杨哲等[11]简化了转换波VTI多参数速度建模流程，有效提高成像质量降低了转换波多参数建模的多解性。静校正方面，Richard 等[12]提出了基于纵波构造约束的转换波静校正方法，并在实际应用中取得了较好的效果，但是该技术需要转换波具有较高的信噪比；高宪伟等[13]提出以面波反演为基础，结合构造约束的转换波静校正技术，并在四川某工区实际应用中取得了较好的效果。为了优化OBS地震资料转换波处理技术流程，有效提高OBS地震勘探的性价比，本文以我国南海某海底电缆(Ocean Bottom Cable,OBC)工区为例，对OBC(Ocean Bottom Cable,OBC)转换波处理过程中的关键技术进行了深入的研究，有效地提高了该工区海底电缆转换波处理的信噪比，并改善了断层及地层的成像效果，一定程度上推动了我国海底电缆转换波地震资料处理的发展。

2 OBC转换波处理关键技术

2.1 R、T分量旋转

海底电缆多波多分量检波器中的水平X分量一般与接收线平行，Y分量与接收线垂直；随着炮点位置的变化，炮-检点连线的方向与X、Y分量的夹角也不断变化[14]，这样X、Y分量就会同时接收到P-SV与P-SH波，这种复杂的波场关系对转换波的处理极为不利，为了获得一致的转换波场，需要将水平方向的两个分量X、Y能量进行重新分配，使其一个分量沿炮-检点连线方向(R径向)接收SV波，另一个分量垂直炮检点方向(T切向)接收SH波，这个过程就是R、T分量旋转[15]；

设炮-检点连线方向与水平测线方向的夹角为θ，UX、UY分别为水平分量与垂直分量的位移向量，UR、UT分别为径向分量与横向分量的位移向量。当θ在0到90度之间时，X、Y分量和R、T分量间的关系可用下式表示[16]：

(1)

若θ在90到180度之间时，公式(1)可以表示为：

(2)

用矩阵形式表示式(1)与式(2)为：

(3)

在公式(3)中右侧的三个变量都是已知量，根据这三个已知量，就可以将X分量、Y分量上的能量转换到R分量、T分量上；由于转换波在炮-检点方向上的偏振性，所以理论上各向同性介质中转换波的能量绝大部分集中在R分量上，各向异性介质中，随着各向异性的增强，T分量数据能量不断增大。

图1所示为转换波坐标旋转前、后炮集，其中图1(a)、图1(b)为X、Y分量的共炮点道集数据，图1(c)、图1(d)为其经水平分量旋转到R、T分量的炮集数据。从图1中可以看到，转换波数据旋转后的能量大部分都集中到了R分量上，T分量中能量很少，这说明该工区地下介质各向异性较弱。图2所示为转换波水平分量旋转前后共转换点叠加剖面上的的均方根振幅切片，其中图2(a)、图2(b)为X、Y分量的均方根振幅切片，图2(c)、图2(d)为R、T分量的均方根振幅切片。从图2可以看到，水平分量旋转后，X、Y两个分量的能量大部分转换到了R分量，T分量中能量很弱。

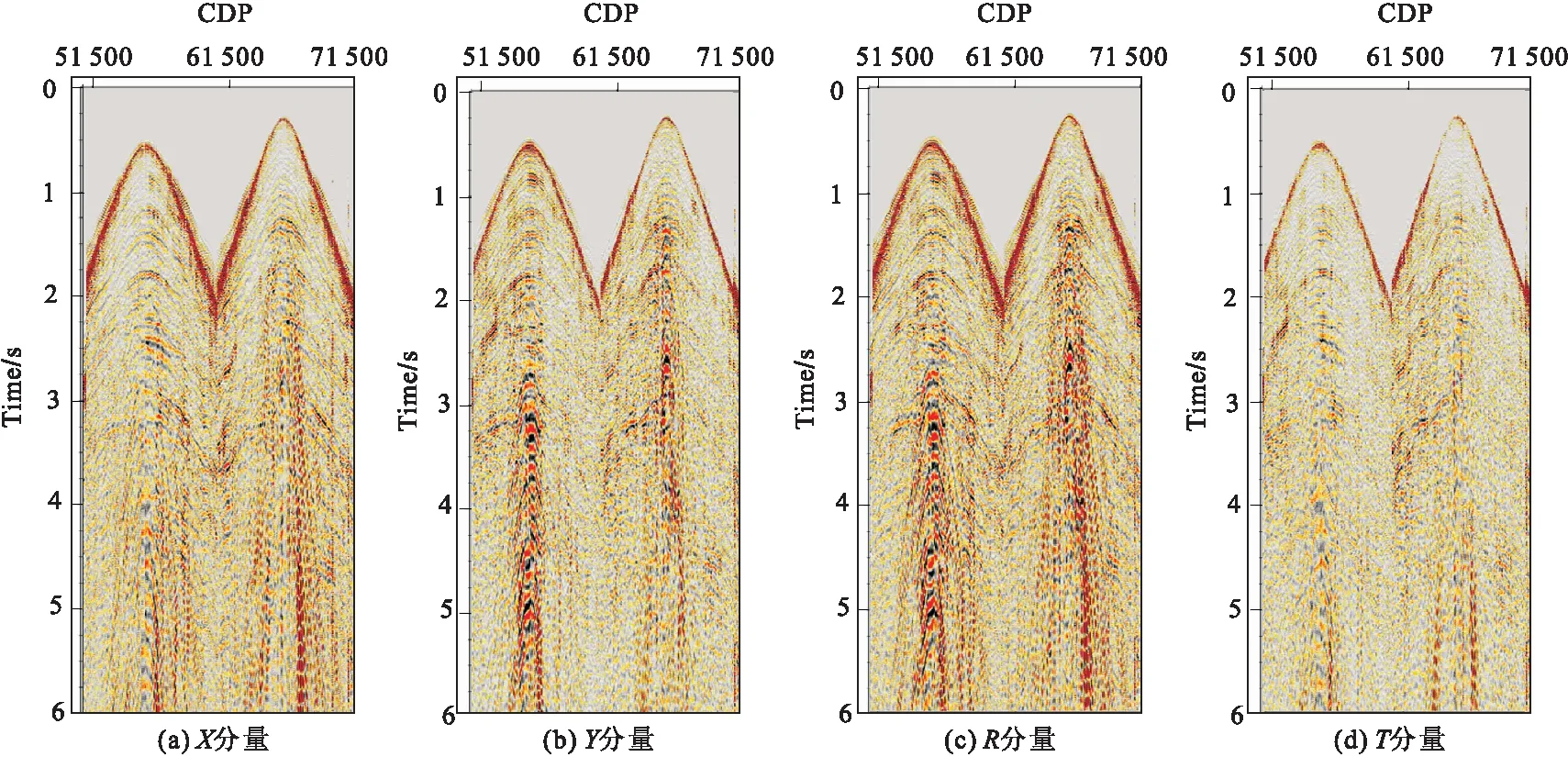
图1 坐标旋转前、后炮集Fig.1 Shot gather before and after coordinate rotation

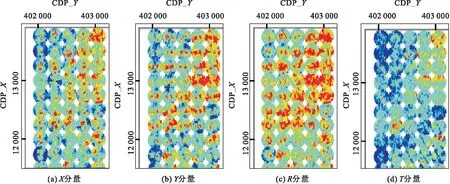
图2 坐标旋转前后均方根振幅Fig.2 Root mean square amplitude map before and after coordinate rotation

2.2 转换波面元化技术

如图3所示，纵波的振动方向与其传播方向一致，他的反射点位于炮点和检波点的共中心点；转换波入射波为纵波，而反射波为横波，其反射点位于共转换点，转换波ACCP(Approximate Common Conversion Point,ACCP)传播射线路径具有非对称性[17]。

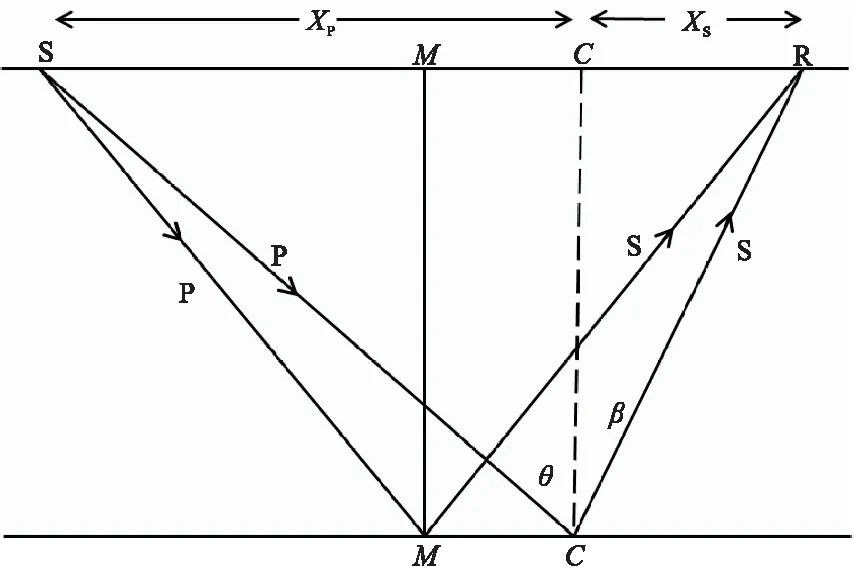
图3 P-P波与P-S波传播路径Fig.3 Propagation path of P-P wave and P-S wave

如何确定转换点的位置是转换波地震资料处理的关键技术之一，设VP、VS分别代表纵波速度和横波速度，θ、φ分别代表P波入射角和S波入射角，p代表射线参数，根据Snell定律可得：

(4)

假设XC为转换点的横坐标;X为源-检距(偏移距);XP为炮点到转换点的水平距离;XS为转换点到接收点的水平距离;φ为P波入射角;θ为S波入射角;LP为P波射线长度;LS为转换波射线长度;tP为P波射线旅行时;tS为转换波射线旅行时;炮-检距X则可表示为[18]：

(5)

由于XC与XP相等，所以XC与X之比可以用下式来表示：

(6)

假设tS0/tP0=VP/VS=γ，可得

XC0=X/(1+1/γ)=Xγ/(1+γ)

(7)

XC0为初始转换点的横坐标，由式(7)可知，随着入射角的减小或者反射层的加深，转换点形成一条如图4所示的渐近线。

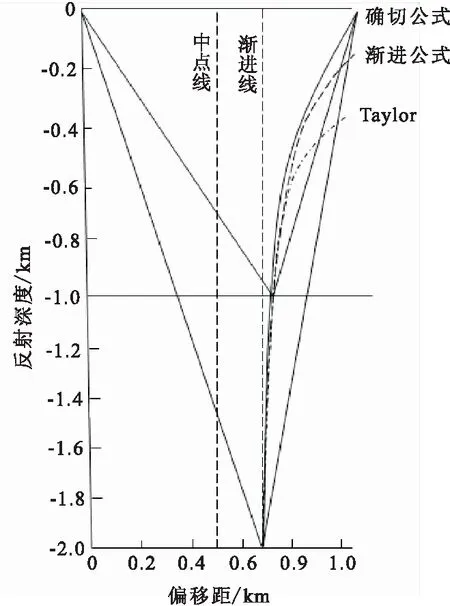
图4 转换点随深度变化曲线 Fig.4 Curve of conversion point with depth

在实际的转换波资料处理中，一般使用垂直γ场可进行转换波的渐进转换点(Approximate Common Conversion Point,ACCP)面元化，并通过偏移使其归位于真实转换点[19]；ACCP道集也可以理解为近似共转换点道集，虽然不如共转换点(CCP)道集精确，但是转换波资料处理时，初始的速度场，纵横波速度比等参数的迭代，其初始值都是从ACCP道集中求取的；并最终通过不断循环迭代，不断逼近真实的CCP道集。

公式(8)为推导得到的γ0理论计算公式，

(8)

或γ0=VP0/VS0

其中，VP0为初始P波速度;VS0为初始转换波速度;tPS为PS波射线旅行时;tP为P波射线旅行时。通过对垂直γ的精细扫描(图5)，比对γ0=3和γ0=3.5的叠加剖面，可以看出γ0=3.5的叠加剖面上目的层区域同相轴成像更加连续，能量较强；参考工区的覆盖次数图(图6)，γ0=3.5的覆盖次数分布较为均匀，横向跳动相对较少；最终确定本工区的γ(VP/VS)值约为3.5，所以首先采用该值来进行初始ACCP道集的抽取。

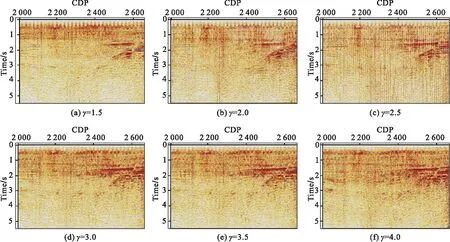
图5 不同γ值的转换波ACCP叠加剖面Fig.5 ACCP stack sections of converted waves with different γ values

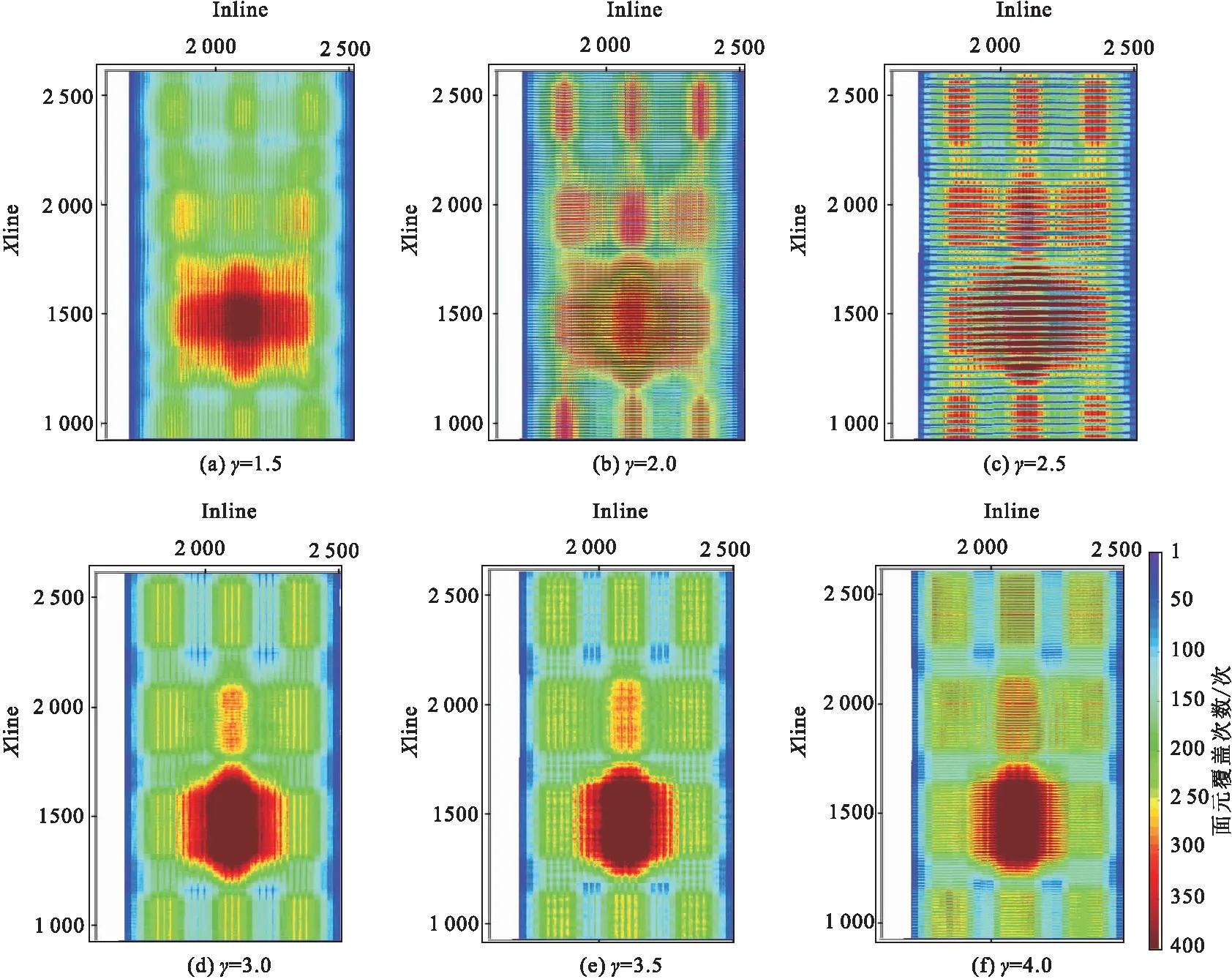
图6 不同γ值的转换波ACCP面元覆盖次数图 Fig.6 ACCP bin coverage of the converted wave with different γ values

2.3 检波点静校正

在4C-OBC(4 Component Ocean Bottom Cable, 4C-OBC)地震资料处理中，静校正是转换波处理的重要步骤；由于转换波传播路径不对称，转换波静校正的炮点静校正量和检波点静校正量需要分别求取[20]。

每道数据的静校正值tij，可用4个部分来表示：

(9)

式中，si代表第i炮的静校正量；gj代表第j个检波点的静校正量；ck代表第k个CCP的剩余动校正量；yk代表构造倾角在第k个CCP点产生的静校正量。

炮点一侧的静校正量主要由纵波带来的，静校正数值和纵波基本一致，检波点一侧的静校正量则有转换横波带来的，由于转换波横波传播速度远低于纵波速度，易受各向异性、岩性横向变化等地质因素的影响，静校正的数值远大于纵波数值，且在该位置处，静校正数值对于成像效果产生的影响相对较大。因此转换波检波点静校正量的求取是关键[21]。

假设表层模型为地表一致性的，为了计算更为简单，该公式假设CCP点的位置和转换点产生的深度无关；地下介质构造较为平缓时，静校正量在检波点的值要远远大于炮点和构造倾角的静校正量之和， 所以，式(9)可进一步进行简化[22]：

tij≈gj

(10)

使用常规旅行时分解静校正量的方法[23]，在共接收点域的叠加剖面上利用优化模型道和目标道间的互相关统计，估算出每个检波点的横波静校正量，再将该静校正量应用在数据上。在共接收点域的叠加剖面上，不同道之间的静校正量与接收点的真实静校正量近似，所以可以使用道与道间的互相关统计来估算接收点的初始静校正值[24]；在初始校正值的基础上对其进行优化，优化的目标函数为叠加道横向能量求和[25]:

(11)

式中：E代表振幅相关能量值;Gk代表第k个叠加道；gk代表第k个点上的静校正值；t代表纵向求和宽度；j代表横向求和宽度。利用这个方法给定初始的gk，求得E值，最后使用最优化函数求出最大E值所对应的静校正量gk。

图7展示的是涠西南工区转换波接收点静校正量的统计图，从图中可以看到，该工区的转换点静校正量在-25～25 ms之间。图8为应用静校正前、后的共接收点叠加剖面，通过对静校正之前的剖面进行观察可以发现，剖面中同向轴的扭曲问题相对较为严重，其同向轴的连续性得到了增强，同相轴的信噪比得到了较大的提高。

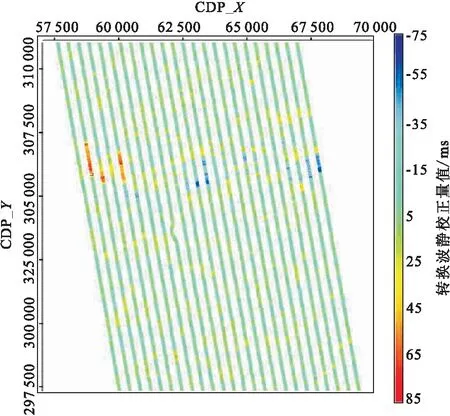
图7 转换波静校正量统计图Fig.7 Statistical static correction values of convert wave

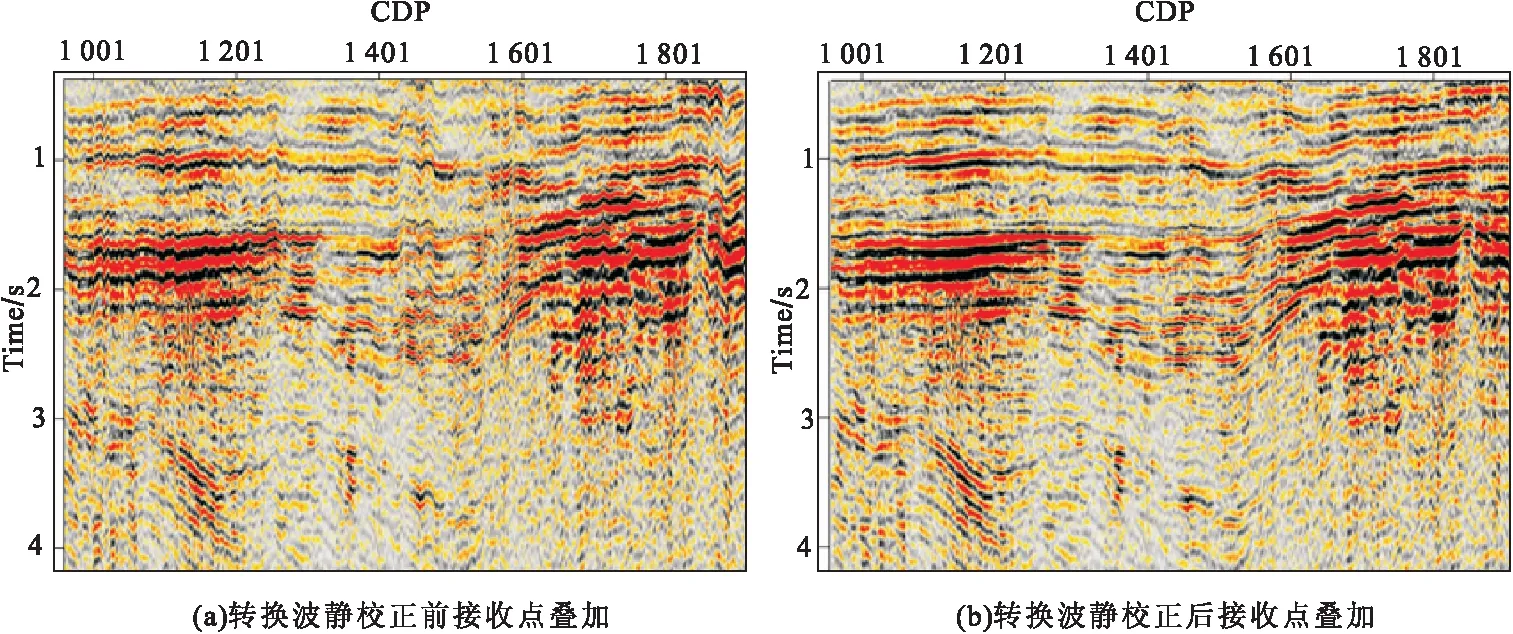
图8 转换波静校正前、后共接收点叠加Fig.8 Convert wave common receiver point stack section before and after static correction

2.4 转换波五维插值与数据规则化

由于4C-OBC地震数据采集成本较高，为了降低采集成本，4C-OBC实际采集时炮线与接收线间距一般较大。这样做虽然节省了采集成本，但也产生了空间采样间隔过大，面元内覆盖次数、方位角、偏移距等信息分布不均及近偏移距数据缺失过多等问题，给后续处理带来了较多的不利因素，对转换波数据的影响更为严重，处理过程中一般需要使用插值技术来弥补空间采样上的不足。对于海底地震(OBS)这些宽方位地震数据，在地震数据插值或者规则化时需要充分考虑其原始采集中的各种信息，本文使用基于抗泄漏傅里叶变换的5D插值方法[26,27]，在一定程度上解决了原始采集数据空间采样过大的问题，同时可以较好地保持OBC数据的宽方位特性。

四个空间维度的不规则数据傅里叶变换方程为：

FT(Kx,Ky,KOx,KOy)

(12)

式中,dn为一个频率切片的输入数据;Kx为x方向上的波数；Ky为y方向上的波数；KOx为offset-x方向上的波数；KOy为offset-y方向上的波数；ω为角频率。

为防止不规则采样数据的傅里叶变换泄漏，通过不断迭代求取最优化的傅里叶系数，每次迭代后使用逆不规则傅里叶变换将其从输入数据中去除，直到不规则网格上最终更新的输入数据执行减法操作后趋为零；最后通过正傅里叶变换，可以将数据映射到任何记录坐标。

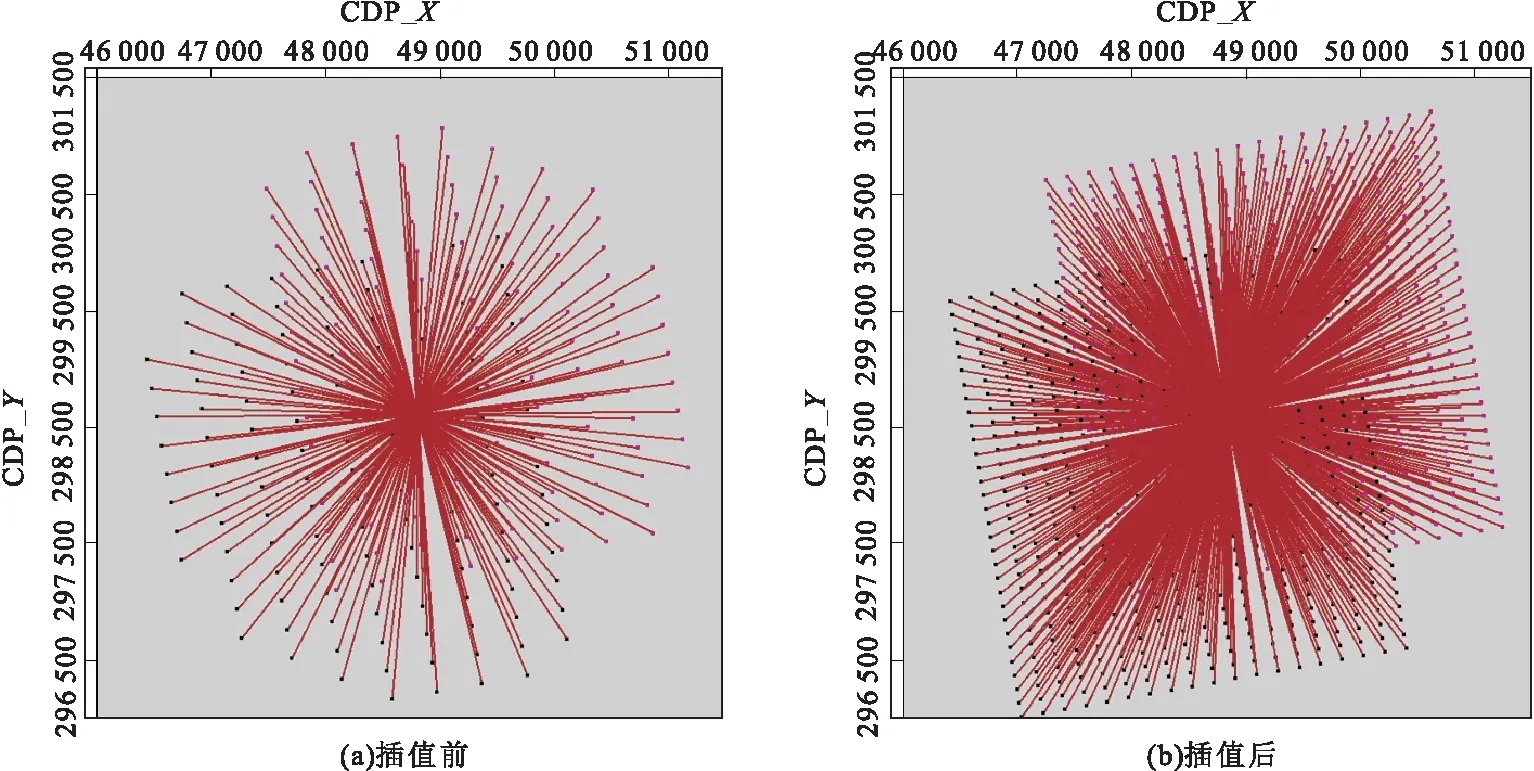
图9 单个面元五维插值前、后的炮检点分布以及蜘蛛图Fig.9 Shot-receiver point and spider figure before and after 5D interpolation in single bin

针对本工区的4C-OBC数据的特征，使用五维插值对地震数据进行重建，重建后的数据炮线和接收线间距各加密一倍，炮线间距由250 m加密至125 m，接收线间距由400 m加密至200 m。图9为单个面元五维插值前、后的炮点与接收点分布图和蜘蛛图。从图9(a)，可以看到，五维插值后炮点和接收点线的密度都增加了一倍；从图9(b)的蜘蛛图可以看到五维插值后，方位角分布更均匀，道数也更多。图10所示为五维插值前、后的CDP道集对比。从图10可以看到，五维插值前的CDP道集中数据缺失较多，很难看到清晰的反射波同相轴，而五维插值后的CDP道集缺失的数据全部被重建出来，同相轴清晰可见。图11示为五维插值前、后的叠前时间偏移叠加剖面。从图11可以看到，五维插值前，由于数据缺失，共偏移距体叠加剖面上地层连续性不强，很难看到地下介质的特征，而五维插值后的剖面较好地恢复了地震波场，及数据中同相轴的连续性，提高了数据的分辨率和信噪比，明显改善了成像质量。成像品质的改善，说明数据规则化能够安全地提高成像质量。

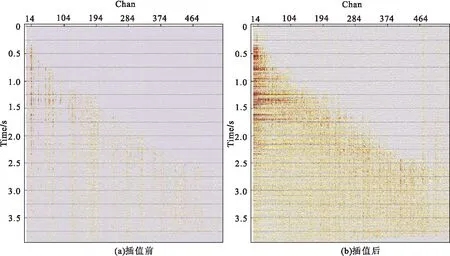
图10 五维插值前后的CDP道集Fig.10 CDP gather before and after 5D interpolation in single bin

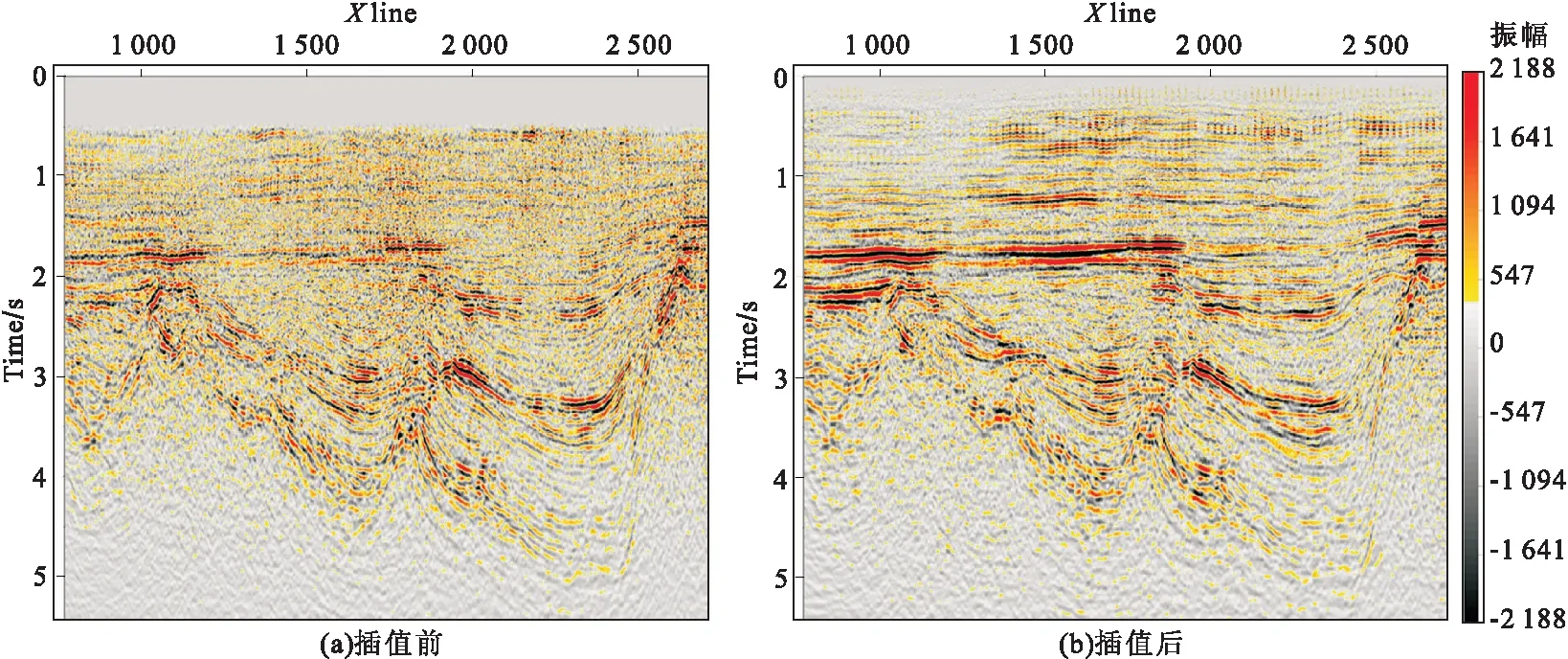
图11 转换波五维插值前、后叠前时间偏移剖面Fig.11 PSTM sections of converted wave before and after five-dimensional interpolation

2.5 转换波时间偏移

转换波传播方式与纵波不同，因此偏移方法也有本质区别。转换波时间偏移的旅行时表达式为：

tC=tP(γ0,VP)+tS(γ0,VS)

(13)

展开为：

(14)

其中：

(15)

(16)

式中，tC为转换波射线旅行时;tP为P波射线旅行时;tS为S波射线旅行时;VP为P波速度;VS为S波速度;γ0=VP0/VS0；VP0为初始P波速度；VS0为初始S波速度；γeffect为迭代后的γ值；VP/VS=γ；VP和VS分别为P波和S波的叠加速度；VC为转换波叠加速度；γ0为垂直速度比。纵波偏移主要参数只有一个，即纵波速度；而转换波偏移则需要三个参数，转换波速度、垂直γ场、纵波速度(或者有效γ场)；这三个参数中，纵波速度来自于PP波处理；垂直γ场来自于纵波和转换波的层位匹配(PP/PS)，是已知量；而有效γ场和转换波速度均为未知量。

采用这种偏移算法需要分别对有效γ场和转换波速度进行扫描：首先使用扫描的垂直γ场，抽取ACCP道集计算初始的转换波叠加速度VC，拾取初始有效γ场；然后使用初始VC、有效γ场、垂直γ场进行PS_PSTM目标线偏移，偏移后的PS剖面与PP波剖面进行层位比对，标识相同层位后拾取较为精确的垂直γ场；第三步使用较为精确的垂直γ场进行PS_PSTM偏移，在偏移的道集上拾取VC和有效γ场，并不断迭代，更新转换波速度；此后需要对有效γ场和转换波速度进行迭代的多次扫描，以求取最终有效γ场和转换波速度，从而进行最终偏移。流程图如图12所示。

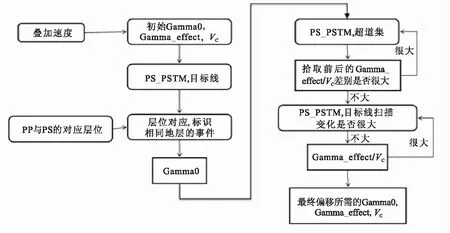
图12 转换波叠前时间偏移速度更新流程Fig.12 Velocity iteration process of converted wave prestack time migration

图13所示为本文靶区使用五维插值处理后的数据做为叠前时间偏移的输入数据，最终迭代更新的PS叠前时间偏移参数场(gamma0，gamma-effectVC)，下一步就可以使用最终求出的参数场，采用克西霍夫法对转换波进行叠前时间偏移成像。

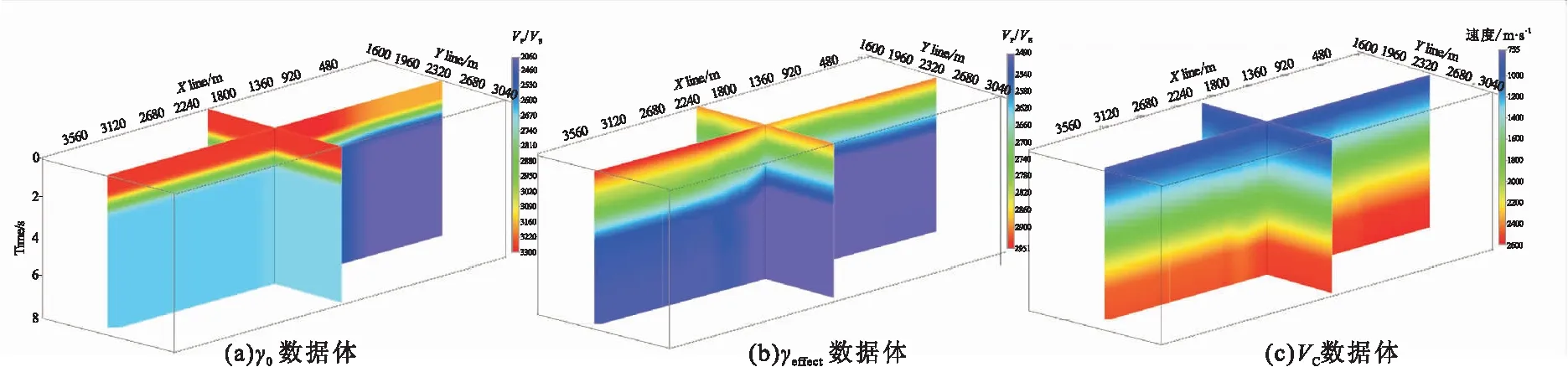
图13 PS波叠前时间偏移参数场(gamma0，gamma-effect,VC)Fig.13 PS wave prestack time migration parameter field (gamma0, gamma-effect,VC)

3 转换波分量地震资料处理效果

为了验证上述OBC转换波处理的关键技术，本文将其应用于南海某工区实际OBC转换波处理中。该工区野外资料由COSL-517海底电缆队采集，记录系统为Searay300，采样率2 ms，记录长度10 240 ms，检波器组合方式为DSU3+1 Hydrophone，四分量采集，patch方式观测系统，共采集了25个patch数据，每一个patch观测系统共48条炮线，8条接收线，炮点间距25 m，炮线间距250 m；接收点间距 25 m，接收线间距 400 m。

图14为该工区转换波处理流程图，其中主要相关处理技术为：R、T分量旋转技术、转换波ACP(Approximate Conversion Point, ACP)面元化、转换波检波点静校正、五维插值、转换波偏移速度扫描技术。

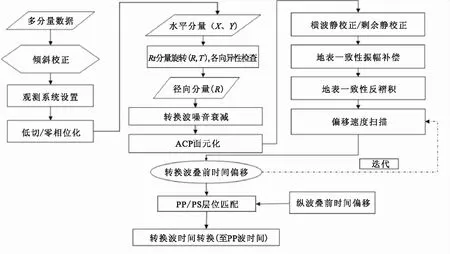
图14 转换波处理流程Fig.14 Converted wave processing flow

图15为 PS波处理效果展示及其与PP波处理效果对比；从PS波与PP波处理效果对比来看，PS波处理的剖面形态与PP波大体一致，并且在中深层有一定的信噪比，在流三段、基底附近波阻特征明显，成像效果较好，断层清楚。但是浅层分辨率及信噪比转换波相对较差，比如1.0 s处纵波和横波反射同相轴能量明显有差异，主要是因为转换波信号低频成分能量较强、分辨率较低引起的；其次，断层成像较有不足，比如基底左侧反射形态有所差异， 主要是因为转换波成像效果精度没有达到纵波的精度。

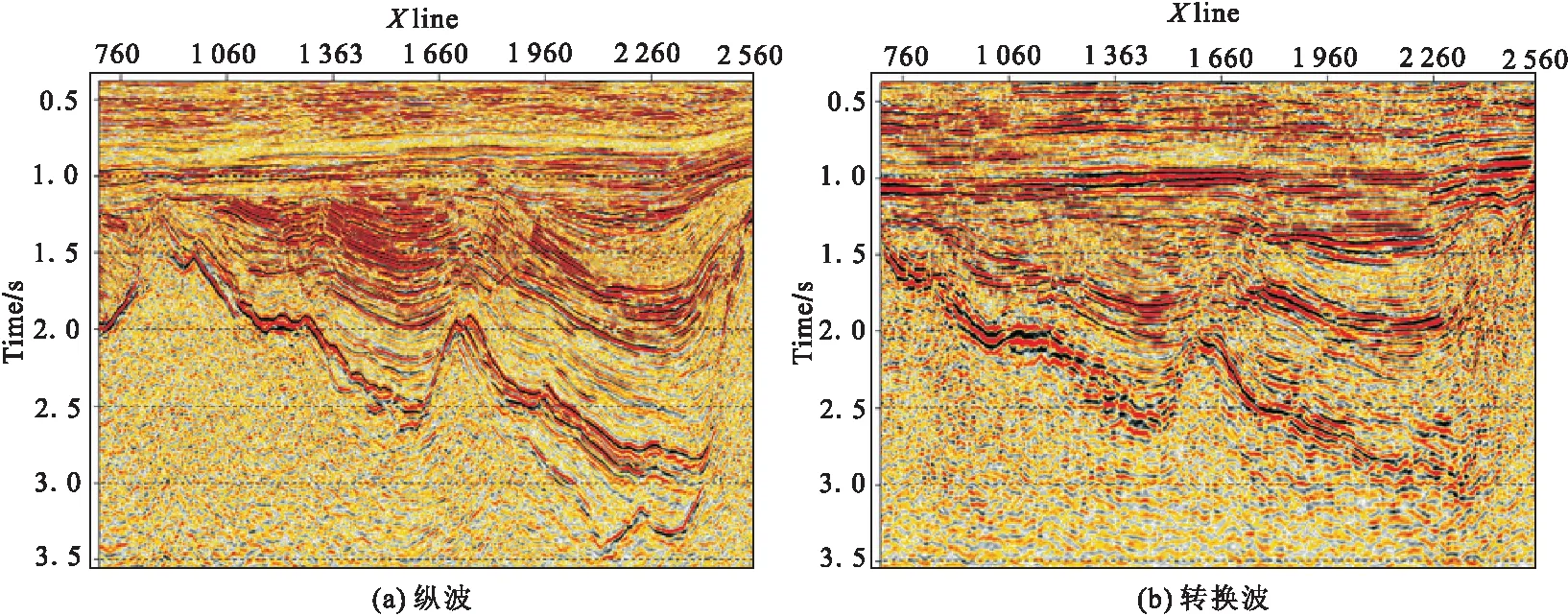
图15 纵波与转换波成果剖面效果对比Fig.15 PSTM results sections of P-wave and converted wave

4 语 结

常规拖缆纵波地震勘探技术面临诸多挑战，比如对尖灭、小幅度构造、小断层、礁体、古潜山的准确定位, 对非构造油气藏的勘探, 真假亮点的识别, 气囱内部成像, 裂缝发育带分析, 流体的识别与监测等；随着海洋油气勘探程度的深入与海底地震勘探(OBS)宽方位多分量采集成本的不断降低，海洋地震资料中的宽方位多分量地震数据会越来越多，所以海底地震转换波处理技术将会得到更广泛的应用。

本文着重介绍了海底电缆转换波处理中的关键技术，使用坐标旋转技术有效地将采集方向的X、Y分量旋转到传播方向的R、T分量，为转换波的下一步处理打下了基础；采用转换波检波点静校正精细解决横波静校正问题。五维插值技术在保持OBC宽方位特征的前提下插值出缺失的地震数据，有效地防止了偏移画弧噪音、提升了道集近偏移距信噪比，并且为宽方位各项异性处理奠定了基础。转换波偏移速度扫描技术能较精确地求取转换波速度和纵横波速度比，转换波叠前时间偏移技术使得R分量精确成像。总体来说，该工区的转换波处理取得了一定的效果，成像较为清晰，地层形态与纵波剖面能较地匹配，但是转换波剖面的分辨率、小断层成像等方面较纵波剖面稍有不足，需要在后续的研究中进行进一步的改善。