基于残差分布定权的M估计球形点云拟合方法

刘存泰，郑德华，王 浩，程宇翔，胡 创

(河海大学 地球科学与工程学院，江苏 南京 210098)

1 引 言

三维激光扫描技术[1]被广泛地应用于测绘及相关领域，获取的点云数据在拼接处理时可采用公共特征目标实现多测站点云的空间直角变换[2]。目前公共特征目标主要有球形目标和平面目标两种类型[3]，其中球形目标因球心固定且唯一、不受激光束的位置束缚、识别距离远等优点，广泛地应用于激光点云配准中[4]。

球形目标球心坐标的精度对点云配准精度和建模与应用的质量有重要的影响[5]。目前，国内外学者主要从拟合方法、模型改进和定权方法三个方面对球形目标球心坐标拟合开展研究：①拟合方法的适应性。主要有最小二乘法[1]、整体最小二乘球形目标定位方法[8]、最小中值方差一致性估计算法[9]等，最小二乘法难以抵御粗差及异常点的干扰，导致定位精度较低；整体最小二乘方法引入系数矩阵误差提高了拟合精度；方差一致性估计方法采用随机采样一致性改进算法提高估计模型参数精度，具有结果稳定性较低的不足。②改进拟合模型方面主要有多项式拟合和几何球面模型的方法[10]、外部综合影响参数因子[11,12]等拟合模型，提高原有模型的抗差能力。③定权方法优化方面主要采用邻域定权[13]、稳健加权[14]以及构建大型稀疏矩阵[17]等方法，得到较整体最小二乘方法更高的精度和效率。

本文针对球形目标扫描点云中存在的偶然误差、系统误差和粗差三类基本误差影响精确配准[18]的问题，设计球形目标激光扫描实验；在充分了解滤波算法的基础上[19]，结合统计滤波较半径滤波及直通滤波[20]方法在保留原始点云细节几何特征信息和避免过度去噪[21]方面的优势，设计基于残差分布定权的M估计球形目标点云拟合方法,以解决不同扫描距离条件下采集球形目标点云三类误差变化的球形目标拟合的抗差能力和适用性问题。

2 M估计球形目标点云拟合方法

2.1 球形目标点云粗差剔除

球形目标点云具有各方向分布均匀、表面特征易识别等特点，由于各站扫描均只能得到半球点云，且边缘部分点云误差较大，因此，噪声剔除环节尤为重要。针对偏离球形目标主体点云较远噪点稀疏且不均匀的空间分布特征，采用统计滤波方法对其进行剔除。统计滤波是对输入的点云数据的查询点与邻域点集之间的距离进行统计分析，将目标点云中粗差和较大的系统性误差作为噪声滤除。首先，遍历点云，计算每个点与其最近的K个邻域点之间的平均距离；其次，计算所有平均距离的均值μ0与标准差σ0，设置距离阈值R进行判别；最后，再次遍历点云，剔除与K个邻域点的平均距离大于R的点。算法具体原理如下：

首先，对点云中所有数据点si(Xi,Yi,Zi)，其中,i=1, 2, 3, …,n(n为点云数量)进行距离统计分析，则si到其任一邻近点hm(Xm,Ym,Zm)的距离rm为：

(1)

按式(2)计算si至其所有邻近点的平均距离r0：

(2)

该平均距离的集合满足正态分布，由数学期望μ0和标准差σ0决定，该分布的概率密度函数为：

(3)

则可按式(4)计算平均距离阈值R：

R=μ0+σ0·std

(4)

式(4)中，std为标准差倍数阈值。若点si到其邻域内的平均距离小于R，记其为有效点，反之为噪声点，予以剔除。针对不同扫描距离下std的取值效果进行实验设计，对比分析不同取值条件下的滤波效果，得到最适合该距离的std值作为最优取值。

统计滤波流程如图1所示。

图1 统计滤波流程Fig.1 Statistical filtering flow chart

在统计滤波的基础上，球形目标点云中较为明显的噪声得到去除，但由于系统误差的存在，一些小尺度的噪声点依然不能完全去除干净，通过改善数学模型的方法减小系统误差，由此引入M估计拟合模型，进一步提高球形目标点云质量。

2.2 M估计拟合模型

M估计是Huber提出的一种稳健估计方法，该方法将残差平方和用另一种关于残差的函数替代，其目标函数为：

(5)

其中，ri为第i点的残差值，对于一组数量为n的点云(xi,yi,zi),其中，i=1,2,…,n。误差方程式为

(6)

其中，vi为扫描观测时的偶然误差，(xi,yi,zi)为球形目标的表面观测数据，(x0,y0,z0)为球心三维坐标，r为球形目标半径。将上式经过线性化处理后可得误差方程模型为：

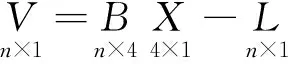
(7)

其中，

2.3 基于点云残差分布确定权函数

根据球形目标点云拟合残差绘制频数直方图，如图2所示。无粗差的点云，其拟合残差为正态分布特征，可得到残差分布的数学期望μ和标准差σ。按式(8)确定权函数ωi，权函数ωi形式如图3所示。

(8)

图2 残差频数分布直方图Fig.2 Residual frequency distribution histogram

图3 权函数图像Fig.3 Weight function image

图4 M估计算法流程Fig.4 M-estimation algorithm flow chart

式(8)中，σ为残差标准差。该权函数将残差小于2.5σ的点权重赋为1；若某点残差在2.5σ～3.75σ之间，则根据其值大小进行定权；若某点残差大于3.75σ，该点不参与参数估计。

则球形目标拟合参数的解为：

X=(BTωiB)-1BTωiL

(9)

由于权函数确定要根据估计参数的残差迭代计算得到，因此，设计基于残差分布定权的M估计拟合算法流程，如图4所示。

3 点云拟合实验与分析

3.1 实验概况

为了分析不同扫描距离的球形目标点云中3类误差对拟合精度的影响，验证本文方法拟合精度和抗差能力，实验设计了一个移动框架结构装置，3个原装进口球形目标设置在支撑框架位置，如图5所示。实验数据采集采用德国的Z+F IMAGER 5016三维激光扫描仪，激光波长为1 550 nm。3个球形目标半径值为72.5 mm，编号从左到右依次为1号、2号、3号。实验选取60 m范围实验场地，扫描距离从10 m到60 m,每隔10 m采集一次球形目标点云，共获取了3个球形目标在6种等间隔扫描距离采集的点云数据，如图6所示。

图5 实验装置Fig.5 Experimental device

图6 实验整体点云Fig.6 The overall point cloud of the experiment

实验所得1号、2号、3号球形目标点云，如图7所示。

图7 各球形目标点云Fig.7 Each spherical target point cloud

3.2 实验结果与分析

针对扫描获取的3个球形目标点云，分别采用本文方法、最小中值方差一致性估计算法(Least Median of Squares，LMedS)以及最小二乘法拟合处理，3个球形目标半径拟合误差与扫描距离关系如图8及表1所示。

图8 3种方法半径拟合误差比较Fig.8 Comparison of radius fitting errors of three methods

由图8及表1可知，以1号球、扫描距离10 m为例，本文方法半径拟合误差较LMedS算法减小0.08 mm，较最小二乘法减小0.14 mm；以1号球、扫描距离40 m为例，本文方法半径拟合误差较LMedS算法增加0.15 mm，较最小二乘法减小1.43 mm。3个球形目标在10～60 m扫描距离条件下，本文方法半径拟合误差均小于最小二乘法半径拟合误差；在10～30 m扫描距离条件下，本文方法半径拟合误差均小于LMedS算法半径拟合误差，在40～60 m扫描距离条件下，1号球和3号球采用LMedS算法所得半径拟合误差小于本文方法。

针对扫描距离40 m之后半径拟合误差较大的情况，本文对扫描点云进行统计滤波，邻域点数目(K)设为50，标准差阈值(std)的选取根据扫描距离确定，各距离最优取值见表2；以扫描距离10 m时获取的点云为例，得到滤波前后点云残差分布情况，如图9、图10所示。

由图9、图10可知，在扫描距离为10 m的条件下，统计滤波对于残差在±1.5 mm以上的噪声点有明显的过滤效果。对去噪后的点云采用本文方法进行球形目标拟合，3个球形目标去噪前后的半径拟合误差与扫描距离关系如图11所示。

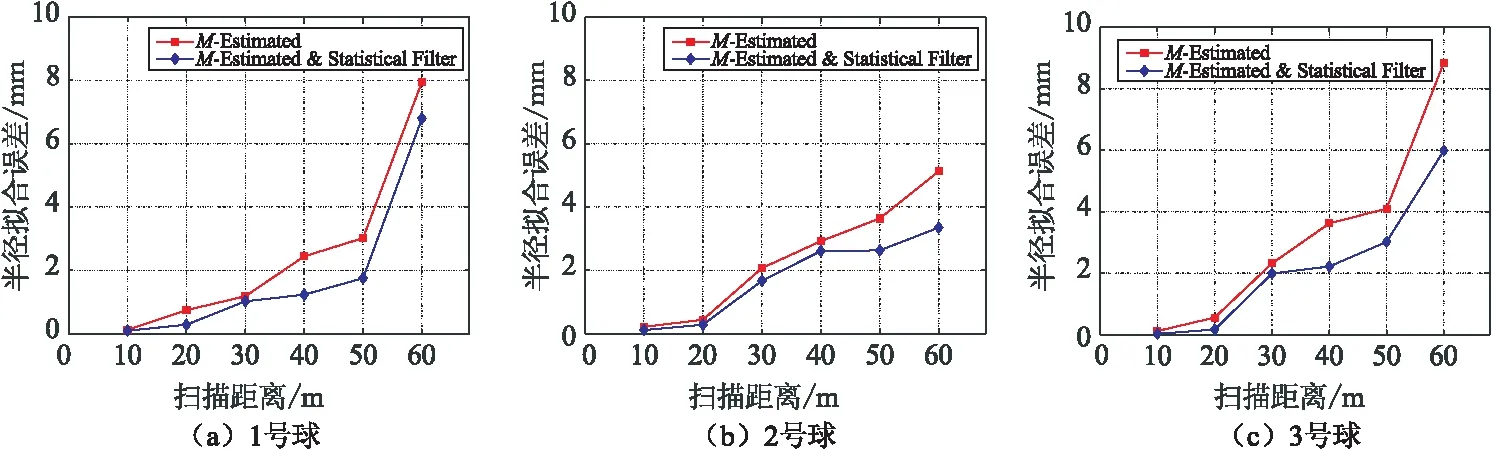
图11 滤波前后半径拟合误差Fig.11 Radius fitting error before and after filtering

由图11可知，以1号球、扫描距离10 m为例，滤波后半径拟合误差较滤波前减小0.03 mm；以1号球、扫描距离40 m为例，滤波后半径拟合误差较滤波前减小1.21 mm。3个球形目标在10～60 m扫描距离条件下，滤波后半径拟合误差均小于滤波前半径拟合误差，且随扫描距离增加，减小幅度逐渐变大。

根据点云拟合残差计算中误差，建立实验中3个球形目标点云拟合中误差与扫描距离关系，如图12及表3所示。

图12 滤波前后点云拟合中误差Fig.12 Error in point cloud fitting before and after filtering

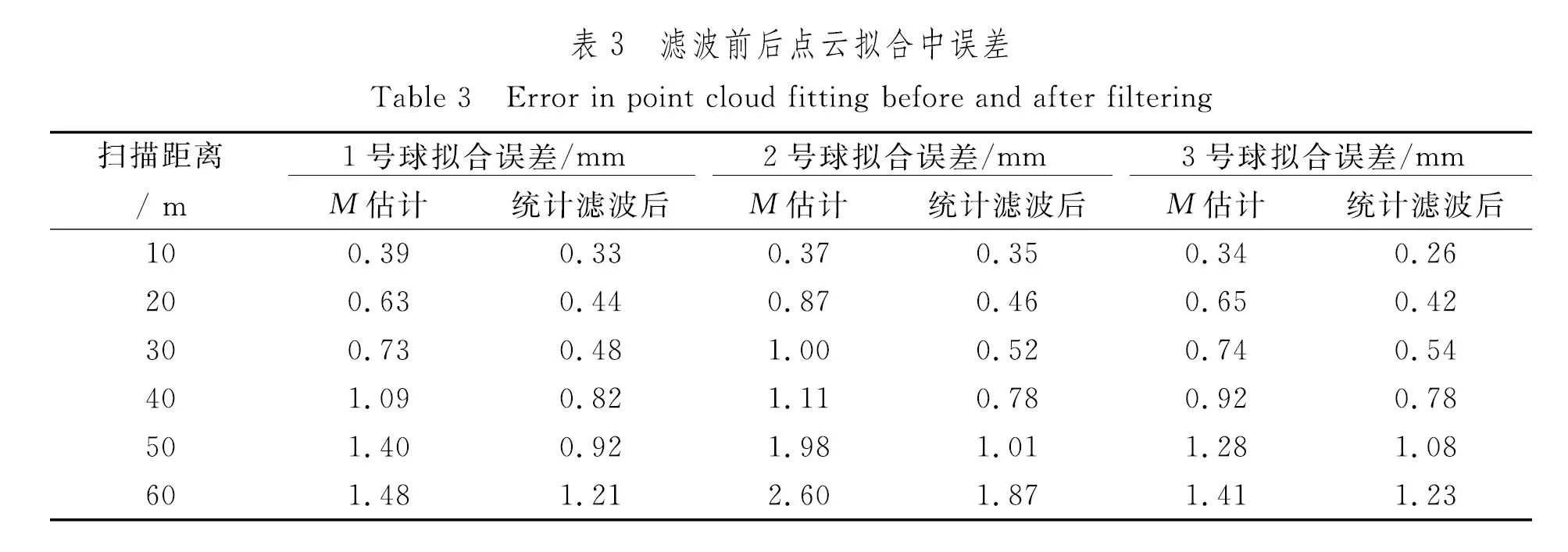
由图12及表3可知，以1号球、扫描距离10 m为例，滤波后点云拟合中误差较滤波前减小0.06 mm，精度提高15.4 %；以1号球、扫描距离40 m为例，滤波后点云拟合中误差较滤波前减小0.27 mm，精度提高24.8 %。3个球形目标在10～60 m扫描距离条件下，滤波后点云拟合中误差均小于滤波前点云拟合中误差。

4 结 语

1)针对现有球形目标球心拟合方法精度不足的问题，提出基于残差分布定权的M估计球形目标点云拟合方法，半径拟合误差较LMedS算法减小21.1 %，较最小二乘法减小48.1 %。本文方法既克服了最小二乘法抗粗差能力不足的缺点，又解决了LMedS算法稳健性不足的问题。

2)引入统计滤波剔除粗差，滤波后球形目标半径拟合误差较滤波前减小49.6 %，点云拟合精度提高24.8 %。统计滤波的引入，提高了球形目标点云拟合精度，特别是改善了40～60 m扫描距离球形目标点云拟合精度稍低的不足。

3)设计的等距离间隔条件下扫描球形目标实验，获取了3个球形目标在不同扫描距离下的点云数据，通过不同扫描距离条件下球形目标点云的半径拟合精度对比，验证了本文方法的稳健性和适用性。