界面滑移对动压气体轴承间隙流动特性的影响*

张镜洋 孙义建 吕元伟 罗欣洋

(1.南京航空航天大学航天学院 江苏南京 210016；2.航空机电系统综合航空科技重点实验室 江苏南京 210016)

动压气体轴承是一种气体自润滑式的轴承。与传统滚动轴承和油润滑轴承相比，动压气体轴承有转速高、结构简单、无油润滑等优点，在航空机载领域有着巨大的发展前景[1-3]。非接触式轴承结构转静子间隙流动状态直接决定其轴承性能，动压气体轴承转静子间隙流动机制及对其性能的影响受到了国内外学者的广泛关注[4-6]。

众多的研究者利用实验和数值模拟手段揭示了动压气体轴承转静子间隙流动机制及其对性能的影响[7-12]。数值研究方面，徐磊[9]基于雷诺方程对刚性轴承进行了分析，发现轴承承载力与摩擦力矩随着偏心率和转速的增大而增大，而偏位角则呈现相反的规律。PENG和 KHONSARI[10-11]基于弹性变形和流体可压缩性建立波箔型径向气体轴承理论模型，通过耦合求解雷诺方程与箔片变形方程得到气膜压力和气膜厚度分布。皮骏等人[12]指出，与传统波箔轴承相比，交错式箔片轴承的承载力明显增加，尤其在转速和长径比增大的情况下尤为明显。实验研究方面，LEE和NISHINO[13]、TANG等[14]和SILVA等[15]利用微小粒子图像测速技术(micro-PIV)测量了动压气体轴承转静子间隙的流态衍变，发现其速度和压力分布高度依赖于转速、间隙尺度和偏心率等参数的变化。

上述数值模拟研究均在流固界面无滑移假设下开展，然而近年来大量的数值模拟和实验研究表明，小尺度、大偏心和高转速条件下，动压气体轴承转静子间隙气膜局部区域克努森数介于0.001～0.1之间，流固界面滑移效应对转静子间隙流动状态及其轴承性能的影响不可忽略[16-19]。例如，SPIKES和GRANICK[17]发现高速旋转条件下动压气体轴承转静子表面流动存在界面滑移，这使得气膜压力明显增加。WU[18]建立了适用任意克努森数的滑移速度模型，获得了与广泛应用的FK模型相近的结果。燕震雷和伍林[19]基于一阶滑移模型和WU滑移模型，建立了耦合稀薄效应的带滑移雷诺方程，考虑稀薄效应后，间隙气膜压力周向分布异于无滑移情形。张镜洋等[20]分析了不同界面滑移状态下轴承静特性变化规律，发现静子侧滑移提高了气膜压力，转子侧滑移则降低了气膜压力，滑移对间隙气膜压力峰值影响幅值可达7%。RAO等[21-22]指出，转静子表面局部滑移情形下，间隙气膜压力分布产生了非单调变化的复杂规律。

基于前述研究，小尺度、大偏心和高转速条件下，滑移对轴承间隙气膜流动存在显著影响。但是，当前研究均基于周向平均和转静子两侧一致滑移情形，这与间隙气膜周向局部克努森数差异较大的事实不符[23]。因此有必要揭示转静子表面流固界面非一致滑移状态下，动压气体轴承转静子间隙流动物理机制以及对轴承性能的影响。本文作者以动压气体径向轴承为研究对象，建立基于极限剪应力模型的界面非一致滑移修正雷诺方程，并耦合气膜厚度方程形成其间隙流动特性分析方法；通过数值分析研究转静侧滑移状态、偏心率、间隙尺寸和耦合弹性箔片对间隙气膜流动特性的影响，以期揭示不同轴承参数下非一致滑移对其间隙流动特性影响机制。文中研究可为动压气体轴承设计和高效运行提供理论基础。

1 数值计算方法

1.1 物理模型

波箔动压气体轴承的结构如图1所示。图中O′为轴承孔中心，O为轴颈中心。O′和O之间的距离为偏心距e，文中计算时所用的偏心率E=e/c，其中c=R′-R。定义圆周方向为x方向，径向为y方向，轴向为z方向。文中研究的参数范围如表1所示。

图1 轴承结构

表1 计算工况

1.2 数值模型

在文中研究的参数范围内，轴承间隙流动雷诺数Re在1 000～1 570之间，轴承间隙流动处于高度层流状态。基于牛顿黏性定律和层流假设简化Navier-Stokes方程，可得到经典的无滑移雷诺方程：

(1)

对控制方程进行量纲一化，环境压力为pa，令x=Rθ，z=Rλ，P=p/pa，H=h/c,Λ=6ωμR2/(pac2)，则量纲一化的雷诺方程为

(2)

根据文献[24-25]，弹性箔片轴承的气膜厚度h由初始气膜厚度和箔片变形厚度hf2个部分组成，其中hf为箔片变形量，UI为箔片的柔度矩阵：

h=c(1+Ecosθ)+hf

(3)

hf=pUI

(4)

经计算，轴承间隙周向克努森数(Kn=λa/c，其中λa为分子平均自由程)在0.000 32～0.004 4之间，间隙内流体处于连续流和过渡流状态。高转速大偏心情形下，最小气膜厚度附近面滑移不可忽略，而间隙尺寸大的区域则呈现无界面滑移状态。基于此，文中在无滑移雷诺方程的基础上施加非一致滑移边界条件。图2所示为轴承间隙非一致滑移示意图，其中u0是转子表面线速度，us1和us2分别是转子侧和静子侧滑移速度。

图2 间隙非一致滑移示意

当考虑非一致滑移时，转子侧和静子侧边界气体速度分别为u0+us1和us2，将其代入雷诺方程中修正速度项：

u=u0+us1+us2

(5)

极限剪应力理论认为当界面剪应力τ达到极限剪应力τs时界面剪应力不再发生变化，因此应先计算转子侧和静子侧的界面剪应力τ1、τ2并与τs比较：

τs=τ0+kp

(6)

(7)

(8)

滑移时界面剪应力等于极限剪应力，将速度边界条件代入可得滑移速度及转子侧(y=0)和静子侧(y=h)的界面滑移速度为

(9)

(10)

(11)

从理论上来说，将界面滑移速度代入雷诺方程进行计算后，滑移区域的界面剪应力应等于极限剪应力，但代入计算后由于压力场会发生变化，界面剪应力和极限剪应力也会发生变化，两者之间还会存在差值，因此需要进行多次迭代计算直到界面剪应力和极限剪应力相等为止。具体流程如图3所示。

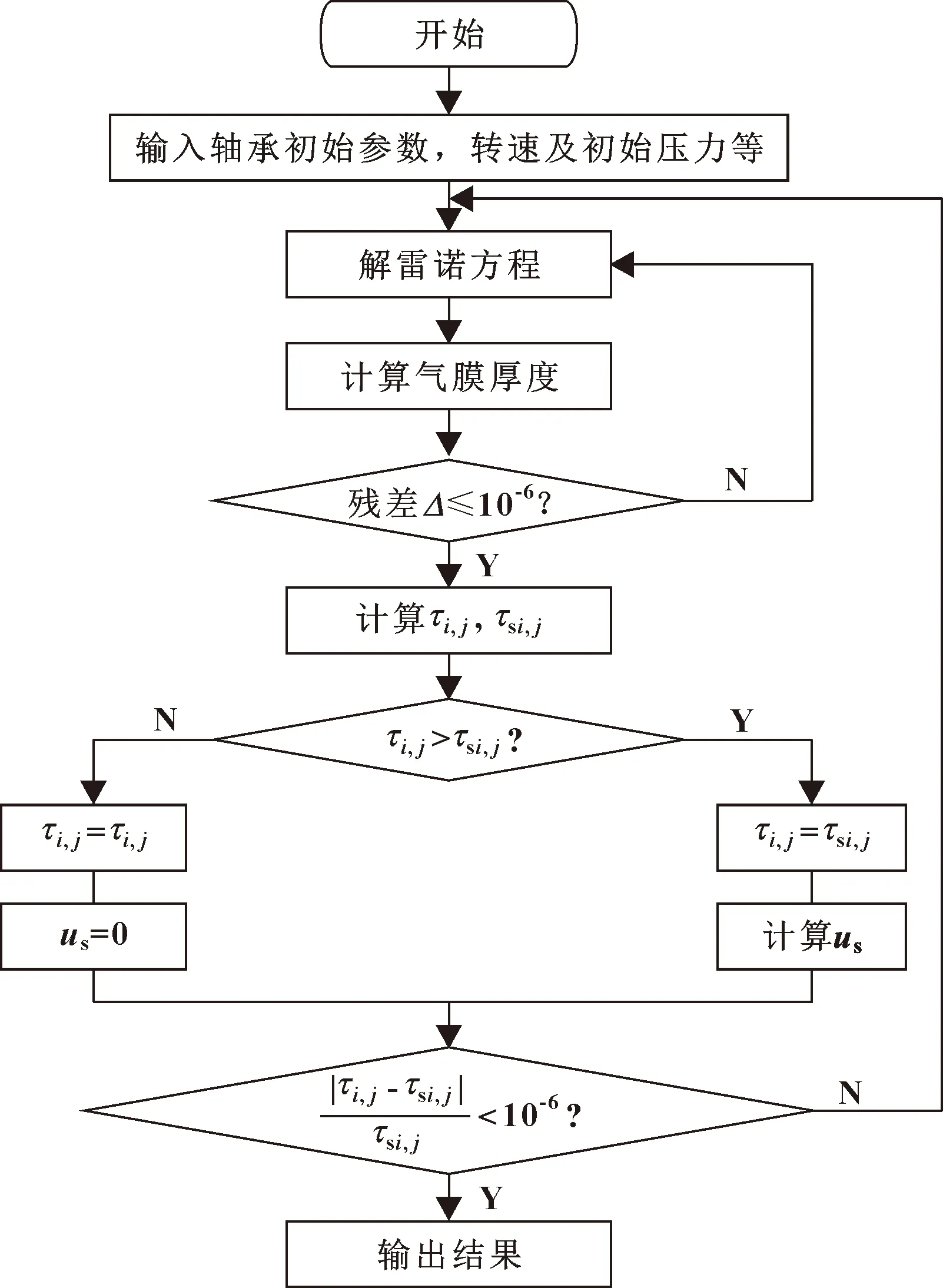
图3 计算流程

1.3 计算网格划分及边界条件

在进行数值计算时将柱坐标系转换为平面坐标系，轴承内表面的网格划分如图4所示，对z方向的轴承长度进行nz等分，对x方向的圆周长度进行nx等分，其中定义x=0为气膜厚度最大处。定义求解域为(0：nx，0：nz)。

图4 计算网格划分

(1)环境边界条件

进口处：P(x,0)=1；

出口处：P(x,nz)=1。

(2)循环边界条件

P(0,z)=P(nx,z)。

1.4 模型验证

为验证文中数值计算方法的合理性，将文中模型计算的量纲一气体压力与文献[26]和基于线性化玻尔兹曼方程的FK模型计算结果进行对比。在R=2 mm,L=0.4 mm,Λ=2.4工况下，比较了3种方法计算得到的量纲一压力沿周向的分布规律，如图5所示。文中数值计算方法得到的量纲一压力沿周向的分布规律与文献[26]和基于线性化玻尔兹曼方程的FK模型的结果基本一致，最大偏差出现在最大压力和最小压力位置处。文中数值模拟结果与文献[26]结果的最大误差为10.4%(Kn=0.01工况)。这说明文中的计算结果有效，能够合理揭示界面滑移下动压气体箔片轴承间隙流动物理机制。

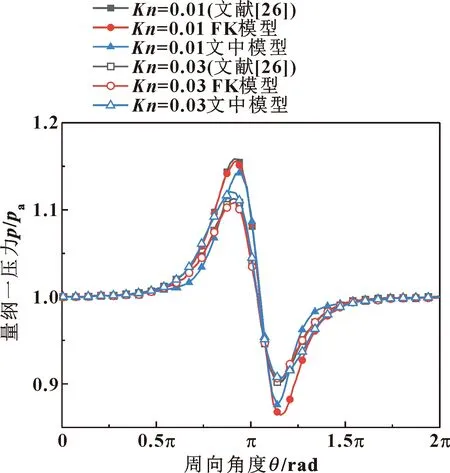
图5 模型验证

2 计算结果及分析

为了理清转静子两侧滑移和周向非一致滑移对流动的影响，在变化滑移状态、偏心率、间隙尺寸时先忽略箔片复杂变形的影响，对刚性轴承开展了分析，然后对箔片变形的影响开展分析研究。

2.1 不同滑移状态下流动特性对比分析

高转速下，静子、转子或者两侧表面的界面剪应力均可能超过极限剪应力，进而导致流固界面发生滑移。文中首先讨论了不同界面滑移状态对间隙流动特性的影响规律，图6示出了n=80 000 r/min，L/d=0.8，E=0.6,c=0.1 mm工况下，轴承中部z/L=0.5位置(A-A截面)和出口z/L=1位置(B-B截面)气膜压力沿周向的分布规律。气膜压力沿周向呈现正弦变化的规律，压力最大值和最小值分别位于θ=0.9π和θ=1.25π区域附近，这与最小间隙上下游区域附近气体经历压缩和扩张的流动状态相一致。轴承中心位置处，静子侧滑移时气膜的压力峰值最大，两侧滑移情形次之，然后是无滑移情形，转子侧滑移时气膜的压力峰值最小。出口位置处4种情形下压力的相对大小与轴承中心位置相同，从A-A和B-B截面可以看到，轴承中部的压力峰值更高，这是因为气体进入间隙后受旋转和偏心的影响，最小气膜厚度处的气体被压缩，密度增大压力上升，由于端泄的影响在轴承中部压力达到峰值，动压效应最强。

图6 不同截面处量纲一压力分布

为进一步揭示不同区域滑移状态对轴承间隙气膜承载力的影响，分别探究了80 000 r/min转速下z=L/2和z=L位置截面处剪应力和量纲一滑移速度，如图7所示。根据极限剪应力模型，无滑移区域界面剪应力小于极限剪应力，滑移区域界面剪应力τ等于极限剪应力τs。由7(a)可知，区域1转子侧界面剪应力τ1和静子侧界面剪应力τ2均小于对应区域的极限剪应力τs，该区域处于无滑移状态;区域2转子侧界面剪应力τ1等于极限剪应力τs,而静子侧界面剪应力τ2小于极限剪应力τs，该区域处于转子侧滑移状态。

定义转子转动方向为正，从图7可以看到静子侧滑移速度为正，转子侧滑移速度为负，因此转子侧滑移会增强局部流动，降低局部压力，静子侧滑移会抑制局部流动，提高局部压力。在z=L/2截面处动压效应强，剪应力沿周向变化大，转子侧滑移发生在压力上升区，静子侧滑移发生在压力下降区，且静子侧滑移速度比转子侧滑移大。在z=L截面处动压效应弱，剪应力沿周向变化小，转子侧滑移速度和静子侧滑移速度几乎相等，均发生在最小气膜厚度处。这是因为在轴承中部剪切流动剧烈，压力梯度大，两侧界面剪应力受压力梯度影响其峰值出现在不同区域：转子侧界面剪应力在压力上升区达到峰值，静子侧剪应力在压力下降区达到峰值。所以有转子侧滑移和静子侧滑移交替出现的现象，且由于最小气膜厚度处压力下降更显著，静子侧量纲一滑移速度接近0.8，而转子侧量纲一滑移速度仅有0.1左右，因而轴承中部界面滑移对压力的影响大。在出口处更接近大气压，压力变化幅度小，转子侧和静子侧滑移均发生在界面剪应力较大的最小气膜厚度处，其滑移速度数值和区域几乎相同，因而出口处界面滑移对压力的影响小。由上述分析可知，转子侧滑移会降低压力，静子侧滑移会提高压力，且越靠近轴承中部剪切流动越剧烈，动压效应越强，界面滑移对压力的影响越明显。

2.2 滑移条件下偏心率对流动特性的影响

图8所示为n=80 000 r/min，L/d=0.8,c=0.1 mm工况下，考虑滑移和不考虑滑移时轴承中部和出口处的量纲一压力分布。偏心率为0.6时，两截面处考虑滑移时的压力峰值均比无滑移时大，最大增幅为4%。偏心率为0.8时，两截面处考虑滑移时的压力峰值比无滑移时小，最大降幅为12%，相比出口处，轴承中部的压力峰值更高。这是因为受旋转和偏心的影响，最小气膜厚度处的气体被压缩，偏心越大压缩效果越强，因此偏心率为0.8时压力峰值比偏心率为0.6时大，且2种情况下轴承中部的压力峰值更大。

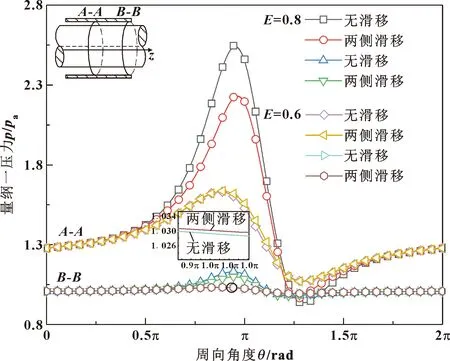
图8 不同截面处量纲一压力随偏心率变化

随着偏心率增大，间隙中最小气膜厚度处的界面剪应力增大，达到极限剪应力的区域增多，界面滑移的速度和区域都变大。由于轴承间隙内压力分布不均匀，滑移速度在不同周向截面呈现不同分布规律，如图9所示。当偏心率为0.6时，在z=L/2截面处，界面滑移沿周向呈现转子侧滑移-静子侧滑移-转子侧滑移交替分布的规律，静子侧滑移速度比转子侧大，两侧滑移的区域大小几乎相同。由前面的分析知道，转子侧滑移会使压力下降，静子侧滑移会使压力上升，此时两侧滑移以静子侧滑移为主，压力比无滑移时大。当偏心率为0.8时，界面滑移沿周向呈现转子侧滑移-两侧滑移-静子侧滑移-两侧滑移-转子侧滑移交替分布的规律，两侧滑移时转子侧和静子侧滑移速度大小几乎一致，仅有转子侧滑移时的滑移速度小、区域大，仅有静子侧滑移时的滑移速度比仅有转子侧滑移时的滑移速度大一倍左右，区域减少约2/3，两侧滑移以转子侧滑移为主，滑移时的压力比无滑移时小。

图9 不同截面处量纲一滑移速度随偏心率变化

由上述分析可知，偏心率增大，界面滑移从以转子侧滑移为主向以静子侧滑移为主过渡，以转子侧滑移为主时，滑移会使压力峰值减小，以静子侧滑移为主时，滑移会使压力峰值增大。

2.3 滑移条件下间隙高度对流动特性的影响

图10所示为n=80 000 r/min，L/d=0.8,c=0.1 mm工况下，考虑滑移和不考虑滑移时轴承中部和出口处的量纲一压力分布。间隙高度为80 μm时，两截面处考虑滑移时的压力峰值均比无滑移时小。间隙高度为120 μm时，两截面处考虑滑移时的压力峰值比无滑移时大，最大幅值为6%，相比出口处，轴承中部的压力峰值更高。这是因为受旋转和偏心的影响，最小气膜厚度处的气体被压缩，间隙越小压缩效果越强，因此间隙尺寸为80 μm时压力峰值比间隙尺寸为120 μm时大，且2种情况下轴承中部的压力峰值更大。

图10 不同截面处量纲一压力随间隙高度变化

图11所示为相同条件下考虑滑移和不考虑滑移时轴承中部和出口处的量纲一滑移速度分布。

图11 不同截面处量纲一滑移速度随间隙高度变化

由图11可以看出，间隙尺寸为80 μm时，界面滑移沿周向呈现转子侧滑移-两侧滑移-静子侧滑移-双侧滑移-转子侧滑移交替出现现象，间隙尺寸为120 μm时，仅出现静子侧滑移，且滑移速度比80 μm小。这是因为间隙尺寸变大，与之伴随的是间隙内的动压效应减弱，界面的剪应力和滑移速度减小。从图10中可以看出，在θ=π处为整个轴向区域压力变化最大的区域，此处的界面剪应力最先达到极限剪应力，所以静子侧界面最先发生滑移，这与文献[27]的研究结果一致。而间隙高度增大会使界面剪应力减小，当间隙尺寸增大到一定程度时，会出现只有静子侧滑移的情况。

2.4 滑移条件下弹性箔片对流动特性的影响

图12所示为n=80 000 r/min，L/d=0.8,E=0.6工况下，考虑或不考虑箔片变形时，气膜压力沿周向的分布规律。与刚性轴承气膜压力沿周向呈现正弦变化的规律相比，弹性箔片轴承间隙内压力受箔片的影响呈阶梯状分布并出现双峰值，压力峰值提高2%左右，压力峰值局部区域的气膜压力降低，这种压力分布状态与文献[28]的研究结果一致。与刚性轴承相比，考虑箔片变形后间隙内气膜厚度发生变化，界面剪应力发生变化，间隙内由以静子侧滑移为主变为以转子侧滑移为主，如图13所示。考虑箔片变形后，轴承间隙内滑移速度的大小和区域都增大，转子侧滑移速度增大近8倍，区域增大近4倍，而静子侧滑移速度增大2倍左右，区域几乎不变。

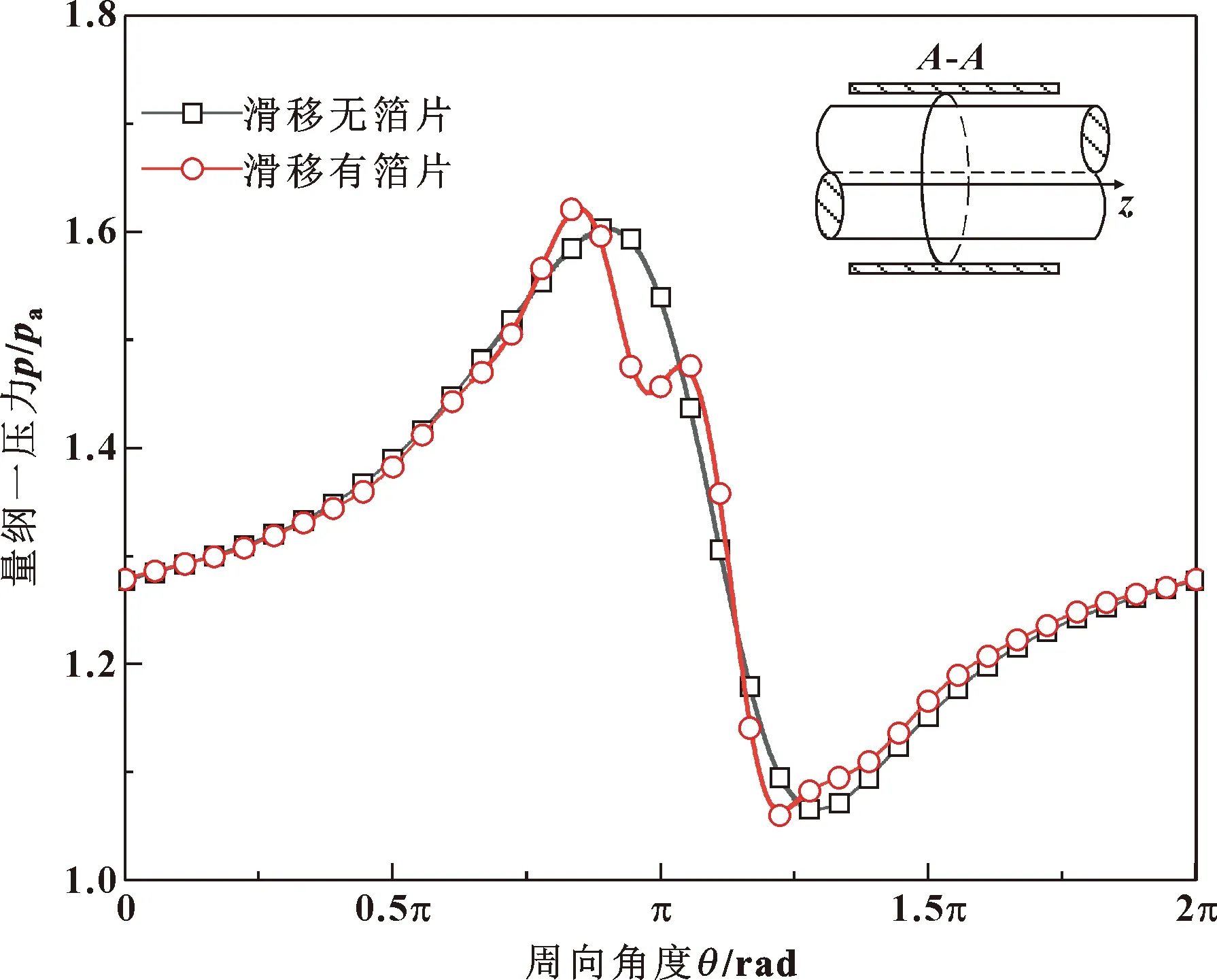
图12 有无箔片时量纲一压力分布

图13 有无箔片时量纲一滑移速度分布

3 结论

(1)建立的非一致滑移模型实现了滑移区和非滑移区的识别，发现界面滑移发生在剪应力较大的收敛楔隙。转静子两侧界面滑移分布区域明显不同，轴承中部两侧滑移区域交替分布，越靠近出口，两侧滑移的区域越大，静子侧界面剪应力更容易达到极限剪应力而发生滑移。

(2)滑移对间隙内压力分布的影响很显著，转子侧滑移会使压力下降，静子侧滑移会使压力上升，越靠近轴承中部压力受影响越大。

(3)偏心率减小、间隙尺寸增大，间隙内界面滑移从以转子侧滑移为主向以静子侧滑移为主过渡。与刚性轴承间隙相比，弹性箔片轴承间隙滑移区域扩大1～4倍，滑移速度变大2～8倍，最高点压力提高约2%。