静压式干气密封温度场数值模拟及试验研究*

贾宇宁 李双喜 张敬博 宋玉鹏

(北京化工大学机电工程学院 北京 100029)

静压式干气密封是一种新型的密封形式，其通过气体静压效应在密封环两端面间形成气膜，使密封端面相互分离，气体将腔体内介质与大气环境隔离，从而达到密封的效果。相较于传统动压式干气密封而言，静压式干气密封可以实现高开启力、高刚度、低泄漏率等效果。温度是影响密封性能的主要因素之一[1]，密封在实际运转过程中，密封环端面会产生一定热量，密封环异常的温度变化会直接影响密封工作状态。同时，由于装配时存在轴不对中等问题，密封环在运行过程中可能会产生碰磨。当密封环发生碰磨时，密封环相互接触摩擦，密封环热量会急剧增加。如果通过温度场能判断密封的运转情况，则可以在密封运转时相对快速地发现问题，从而快速地进行处理，避免密封的损坏。

SAMANT等[2]使用Ansys软件对机械密封环进行了热-固耦合分析，得到残余应力引起的平面度偏差。LAI等[3]和YOUNG等[4]通过建立机械密封耦合模型，预测密封环变形、温度、泄漏量和端面液膜厚度。朱学明等[5]通过分析机械密封环热-结构耦合分析，提出了2种解决办法，通过对比，发现接触耦合法更符合工程实际。THOMAS等[6]利用数值模拟的方法，针对热弹性流体非接触机械密封，建立了二维流固热耦合数值模型，研究了端面变形对间隙几何形状和密封性能的影响。LUAN和KHONSARI[7]对机械密封湍流耦合进行了数值研究，分析了动静环接触面的产热、内部导热以及外部对流传热，计算了密封环外的对流换热系数。BRUNETIRE和MODOLO[8]利用CFD对实验内压机械密封进行了数值分析，通过一系列模拟找到了流体与材料热传导的比值，从而找到了固体温度场的分布规律，并通过实验进行了验证。魏琳宗[9]利用Ansys软件，分析了密封间隙的流场和温度场分布，以及密封环的热变形和弹性变形，通过相互迭代，实现了机械密封流-固-热耦合分析。陈志、刘伟等人[10-11]通过数值分析的方式，分析了动压干气密封的温度场，从而为动压干气密封研究提供了一定理论依据。郑建科[12]和朱维兵等[13-14]利用Ansys软件，针对多种工况下的静压式干气密封进行了端面温度场分析及变形分析。WANG等[15]通过耦合传热法，模拟了动压密封环的非等温流场，对氦气干气密封与空气干气密封热流体力学进行了预测和比较。BLASIAK等[16]通过解析法求解热方程，基于第一类和第二类贝塞尔函数，定义密封圈温度分布和液膜之间的关系，确定了操作参数对温度变异性的影响。HUANG等[17]通过建立流场与密封组件的数值模型，利用耦合迭代的方法建立了在线数值TSFI模型，通过试验的方法验证了模型有效性，分析了密封力学变形、热变形和温度场。随后通过试验验证了研究结果。陆俊杰等[18]利用试验的方法，通过LabVIEW对密封端面编写程序，通过相符的传感器和测试技术，测量了干气密封端面的温度。NELSON[19]通过有限元方法，分析了动压密封环的摩擦学行为，并通过试验进行了验证。

前人针对机械密封或动压密封温度和热变形相关性能进行过很多研究，但针对静压式干气密封温度场对密封性能的影响研究，以及静压密封在异常摩擦状态下的温度场分析较为欠缺。通过温度场判定密封运行状态的相关研究，也尚未见到相关报道。本文作者首先通过数值模拟的方式，分析了静压式干气密封温度场在不同膜厚、不同转速以及不同腔内环境下的变化规律；然后分析了静压式干气密封温度场对密封性能的影响，最后通过实际运转试验，验证了温度场数值模拟的准确性，并创新性地提出基于温度的密封环运行状态的监测方法。基于温度场判断密封运行状态，可以更快速地判别密封是否运行在异常接触条件下，从而快速提出应对措施，减少了因密封失效而造成的损失。该研究为密封环温度场分布与密封工作状态监测提供了新的思路和方法。

1 静压式干气密封结构和原理

静压式干气密封结构如图1所示。密封外压为腔内压力，密封内压为大气压。当密封工作时，压力为ps的调控气进入密封，先在静环上部端面与弹簧共同组成闭合力。随后气体继续向下，通过一定数量、均匀分布且直径相同的节流孔后进入密封端面，利用静压效应在端面形成开启力。由于开启力在密封端面未开启前大于闭合力，故两密封端面在气体的作用下实现分离。开启力随着密封膜厚的增加而减少，开启力最终与闭合力平衡，密封环端面间形成一层微米级的稳定气膜，如图2(a)所示。但当密封运转异常时，如密封气压分布不均或小孔发生堵塞等原因，则会造成密封端面气膜刚度不足，致使密封端面气膜分布不均，发生密封环接触等事故，如图2(b)所示。

图1 静压式干气密封结构

图2 静压式干气密封运行工况状态

2 密封温度场数值模拟计算模型

2.1 计算假设

由于静压型干气密封边界条件较为复杂，为了简化模型，进行以下合理假设：

(1)假设温度场为稳态温度场，即达到稳定后密封动静环温度不随时间变化；

(2)假设密封动静环端面热流密度均匀分布；

(3)密封环材料性质受温度影响较小，因此可以假设密封动静环材料性质不随温度变化。

基于以上假设，正常工况条件下密封环热量主要来源于动静环端面间气膜产生的黏性剪切热Qv，异常接触工况条件下密封环热量主要来源于动静环端面间的摩擦热Qb。此外在2种工况下，热量来源还包括辅助密封O形圈的摩擦热以及弹簧的振动热等，但是这部分热量很小，计算时可以忽略。热量耗散包括动环旋转时与空气的强制对流换热QA1、QA2，静环与空气的弱对流换热QB，静环传递给静环座的热量QC，流体膜带走的热量QD1、QD2，动环传递给动环座的热量QE。根据静压式干气密封结构示意图，静压式干气密封热边界条件如图3和表1所示。

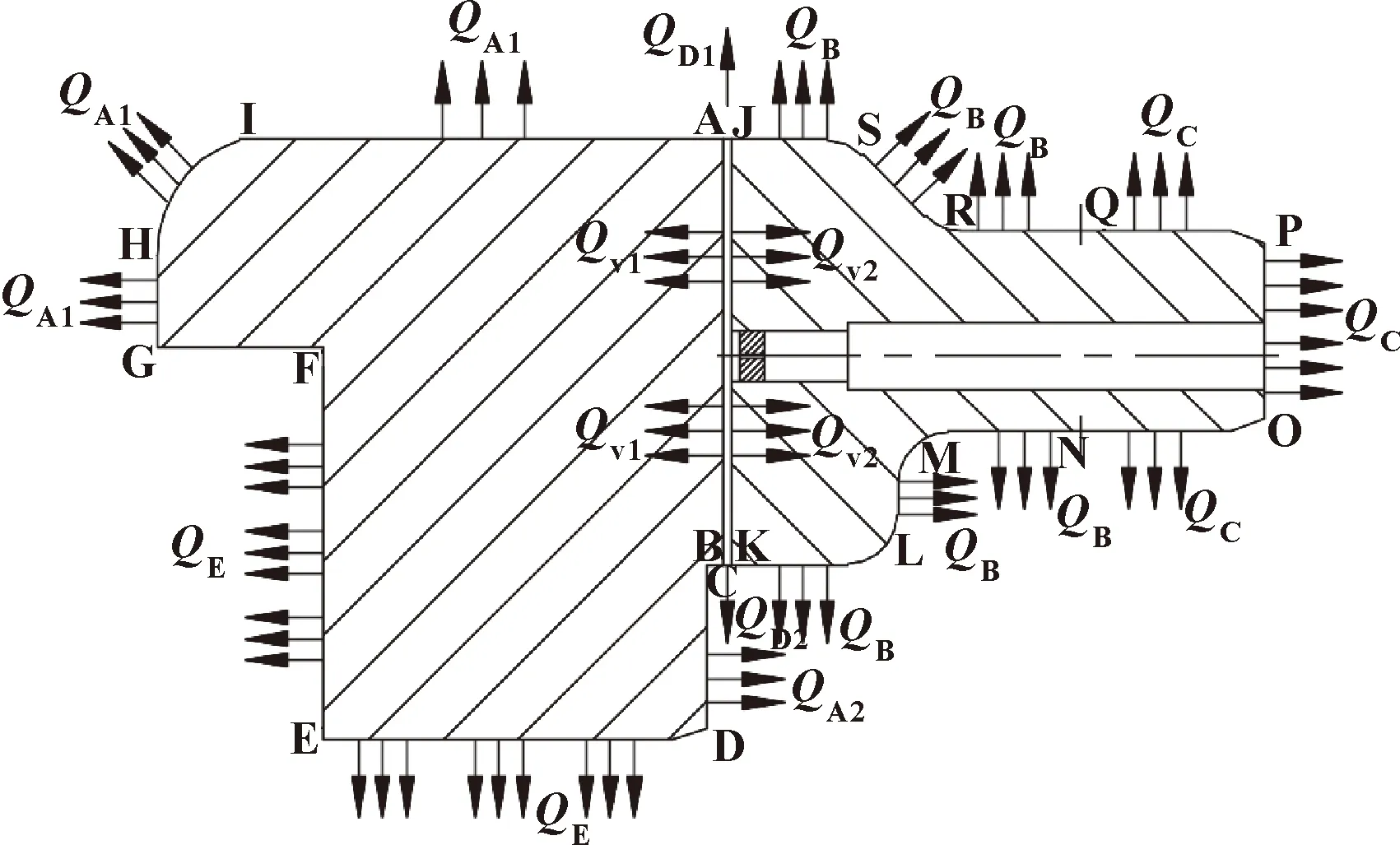
图3 静压式干气密封热边界示意

表1 静压式干气密封热边界条件

正常工况热平衡公式如式(1)所示，异常接触工况热平衡公式如式(2)所示。

Qv=QA+QB+QC+QD1+QD2+QE

(1)

Qb=QA+QB+QC+QD1+QD2+QE

(2)

由于密封内外径处泄漏量为10-5g/s量级，泄漏量较少，因此介质带走的热量可以忽略。静环传递给静环座的热量和动环传递给动环座的热量相较于其他热量较少，均可忽略。忽略小量后，正常工况热平衡公式如式(3)所示，异常接触工况热平衡公式如式(4)所示。

Qv=QA+QB

(3)

Qb=QA+QB

(4)

2.2 黏性剪切热计算

根据前文所述，静压式干气密封在正常工况条件下运转时，主要热量来源于密封端面气膜所产生的黏性剪切热Qv，其通过解析法进行计算。根据文献[21],黏性剪切热的计算公式为

Qv1=qv×Af

(5)

由于动静环结构参数的不同，所以热流密度在2个环上分配不同，因此需对动静环进行热量分配计算。

2.3 密封环热量分配

根据文献[21],密封环热量分配采用热稳态计算公式为

(6)

式中：h1为密封环轴向厚度，mm；y为距离端面的距离，mm；λ为密封环导热系数，W/(m·K)。

由于两密封环材料相同，且端面处两环温度相同，因此当y=0时，可得：

(7)

式中：qr、hr为动环系数；qs、hs为静环系数。

因此可得动静环热流密度分别为

(8)

2.4 摩擦热计算

根据前文所述，静压式干气密封在接触工况条件运转时，主要热量来源于密封端面的摩擦热Qb，其通过解析法进行计算，计算公式为

Qb=qv×f×pcr×n

(9)

2.5 对流换热计算

根据流体物性及流动的形式，对不同的对流换热边界采用不同公式计算对流换热系数。其中，动环与空气的对流换热由于旋转流和轴向流的双重作用，因此计算公式按式(10)。在密封运转时，静环保持静止状态，因此静环与空气流动不存在旋转流，为自然对流，计算公式按式(11)。

(10)

(11)

式中：λ为空气导热系数，W/(m·K)；d0为动环外直径，mm；Ree为密封介质旋转搅拌影响的雷诺数；Ref为横向热流影响的雷诺数；Pr为普朗特常数；Ta为泰勒数；Ss为密封环与旋转轴之间的间隙。

3 密封温度场数值模拟计算结果

利用上述边界条件对静压式干气密封进行计算。密封结构参数、工况参数、相关材料属性及密封介质物性参数如表2—4所示。

表2 静压式干气密封结构参数和工况参数

表3 静压式干气密封环材料属性

表4 静压式干气密封介质物性参数

基于上述条件计算的温度云图和密封环端面温度细节图分别如图4、5所示。可见，密封环最高温度位置位于密封环端面处，两密封环端面处温度基本一致。因此，为了简化计算，以下均以两密封环端面处最高温度为研究对象。

图4 密封环温度云图

图5 密封环端面温度细节图

3.1 不同转速对端面温度的影响

3.1.1 正常工况

根据密封运转工况，在不同膜厚下对密封环在不同转速下的温度进行了数值模拟，结果如图6所示。

图6 不同膜厚下转速对密封环端面温度的影响

随着转速的增加，密封环端面温度逐渐升高。由于密封环的主要热量来源——黏性剪切热与转速呈二次方正相关，而密封环散热主要的影响因素——对流换热的系数与转速关系较小。因此在高转速条件下，温升会更快，密封环端面温度更高。但是高转速条件下，密封环附近的对流换热系数也随之增加，散热性能更好，因此密封环端面并没有产生较大温升，而是保持在一定的范围内。

3.1.2 异常接触工况

异常接触工况下，由于端面间不存在气膜，表4所列空气的物性参数将不再适用。由于端面间摩擦产生的摩擦热将比黏性剪切热更多，因此，密封环端面温升更加明显。根据密封运转工况，对不同转速下异常工况的密封环温度进行了数值模拟。异常接触工况与正常工况密封环端面温度对比如图7所示。

图7 异常接触工况与正常工况密封环温度的对比

由图7可见，在正常工况下密封环的温升比接触工况下的温升高得多，异常工况条件下密封环温升幅度甚至达到600 ℃以上。由于异常接触工况与正常工况热量产生方式有所不同，因此产生的热量也不相同。两环接触时产生的摩擦热远大于两环正常工作时产生的黏性剪切热，而密封环运转时对外界散热的对流换热几乎保持不变。因此密封环端面会产生更多热量，温度也会急剧增长。

3.2 不同膜厚对端面温度的影响

根据密封运转工况，对正常工况条件下，不同膜厚的密封环温度进行了数值模拟。不同膜厚对密封环端面温度的影响趋势如图8所示。

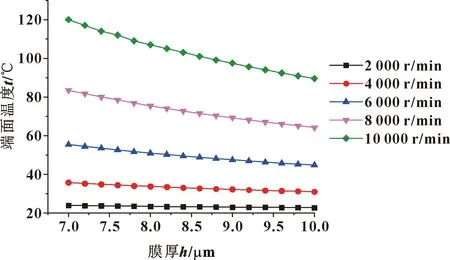
图8 不同转速下膜厚对密封环端面温度的影响

随着膜厚的增加，密封环温度逐渐减少。由于密封环主要热量来源——气膜黏性剪切热与气膜厚度呈现负相关关系。因此，随着气膜厚度的增加，密封环所产生的热量会相对较小，而密封环散热主要的影响因素——对流换热系数不受气膜厚度影响，因此温升会相对较小。

由于在相同的其他工况条件下，进气压力越大，膜厚越小，因此该规律也可以进一步引申为进气压力对于密封环端面温度的影响：随着进气压力的增加，密封环温度逐渐减少。

3.3 不同腔内温度对端面温度的影响

密封实际运转过程中，腔内介质会产生不同的温度。根据实际密封运转工况，对不同腔内温度情况下的密封环温度进行了数值模拟，分别分析了正常工况和异常接触工况下不同腔内温度对密封环温度的影响，结果分别如图9和图10所示。

图9 不同转速下腔内温度对端面温升的影响(正常工况)

图10 不同转速下腔内温度对端面温升的影响(异常接触工况)

腔内温度的上升，即密封环所处环境温度上升。当密封环在更高温环境下运行，端面必然会产生更高的温度，因此这里讨论腔内温度与密封环端面温度之间的差值更为合理。随着腔内温度的增加，正常工况下密封环端面温度受腔内温度影响较小，其与腔内温度的温差平稳上升。而异常接触工况受腔内温度影响较大。虽然密封环端面与腔内温差呈明显下降趋势，但温升数值仍明显大于正常工况。正常工况条件下，空气在不同腔内温度条件下，物性有一定的差距，但相差不大，因此会产生较小的升温幅度。而异常接触工况条件下，热量产生的主要来源为摩擦热，随着腔内温度的增加，腔内温度也通过与密封环其他面的接触，间接影响密封环端面温度。随着温度的升高，腔内热源的影响逐渐变小，因此与腔内的温差逐渐减少。但是即便异常工况条件下温差逐渐减小，相较于正常工况依旧会产生较大的温升。

3.4 不同腔内压力对端面温度的影响

密封运行过程中，腔内介质会产生不同的压力，腔内压力对于密封环温度也会产生一定的影响。根据实际密封运转工况，分别在不同腔内压力条件下，对正常工况和异常接触工况条件下的密封环温度进行了计算，结果分别如图11和图12所示。

随着腔内压力的增加，正常工况与异常接触工况下的密封环端面温度均有不同程度的下降，但下降趋势都并不明显。在不同压力条件下，空气物性会有一定差距，传热系数会逐渐增加，传热效率提高，因此密封环端面温度下降。正常工况条件下，由于端面间气膜的存在，随着空气压力的增加，传热系数逐渐增加，但增幅不大，所以密封环温度不会有很明显的下降。而异常接触工况主要生热来源为摩擦热，摩擦热主要受两密封环旋转影响，因此端面温度受腔内压力影响不大。

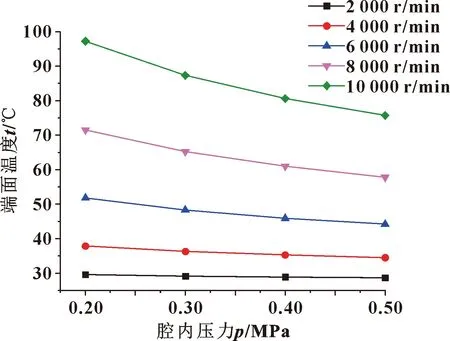
图11 不同转速下腔内压力对端面温升的影响(正常工况)

图12 不同转速下腔内压力对端面温升的影响(异常接触工况)

4 密封环端面温度对密封性能的影响

对于静压式干气密封，密封的开启力、刚度，泄漏率是重要的性能指标，而密封环端面温度的变化对密封性能也会产生一定的影响。文中针对相同膜厚、相同进气压力和腔内压力工况，研究了不同密封环端面温度对密封性能的影响。为简化计算，选取进气压力为0.4 MPa，腔内压力分别为0.2和0.3 MPa进行计算。计算结果如图13—15所示。

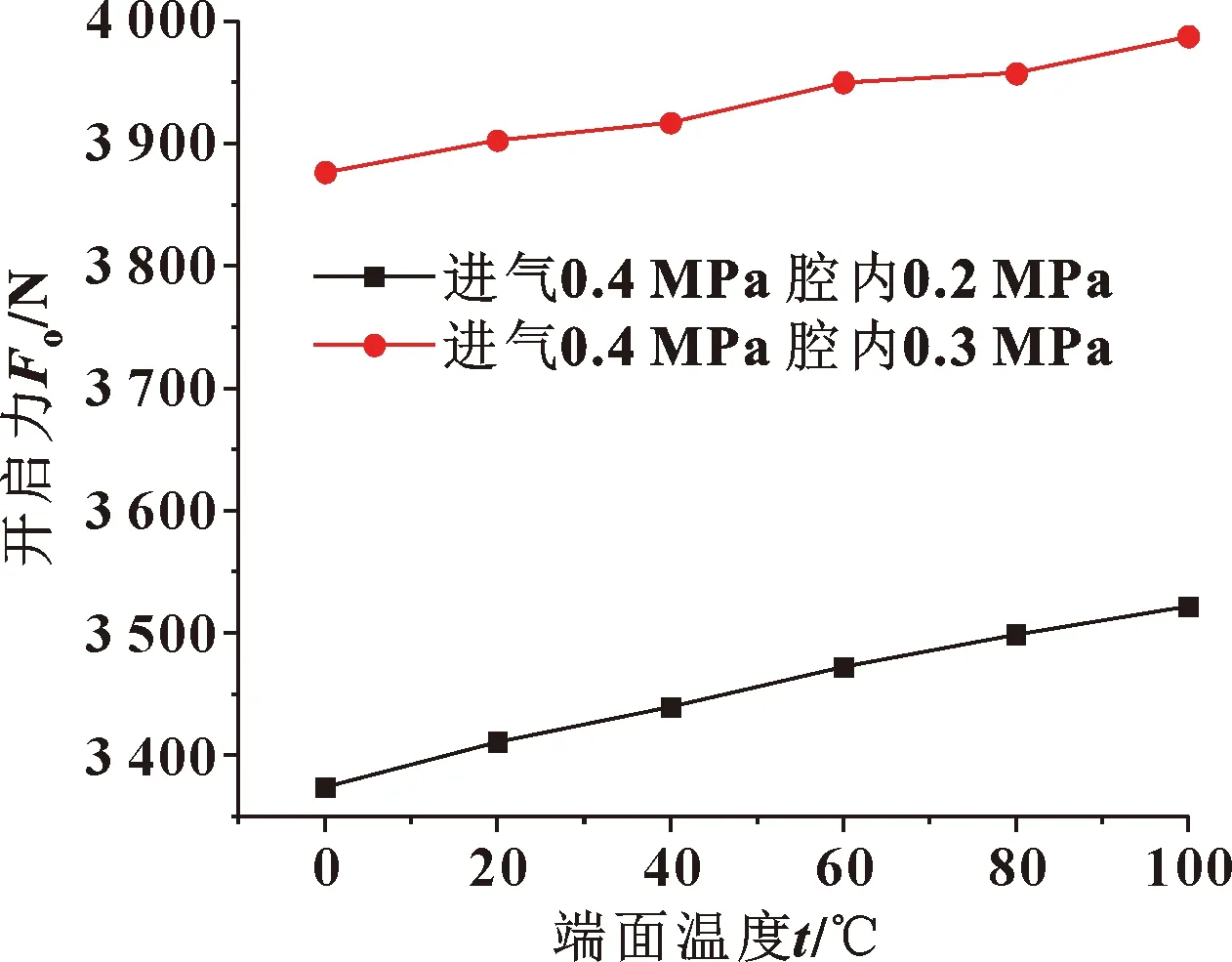
图13 端面温度对开启力的影响

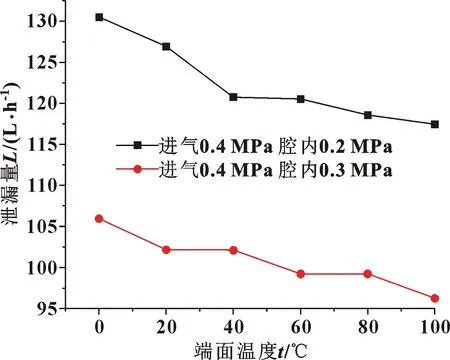
图14 端面温度对泄漏量的影响

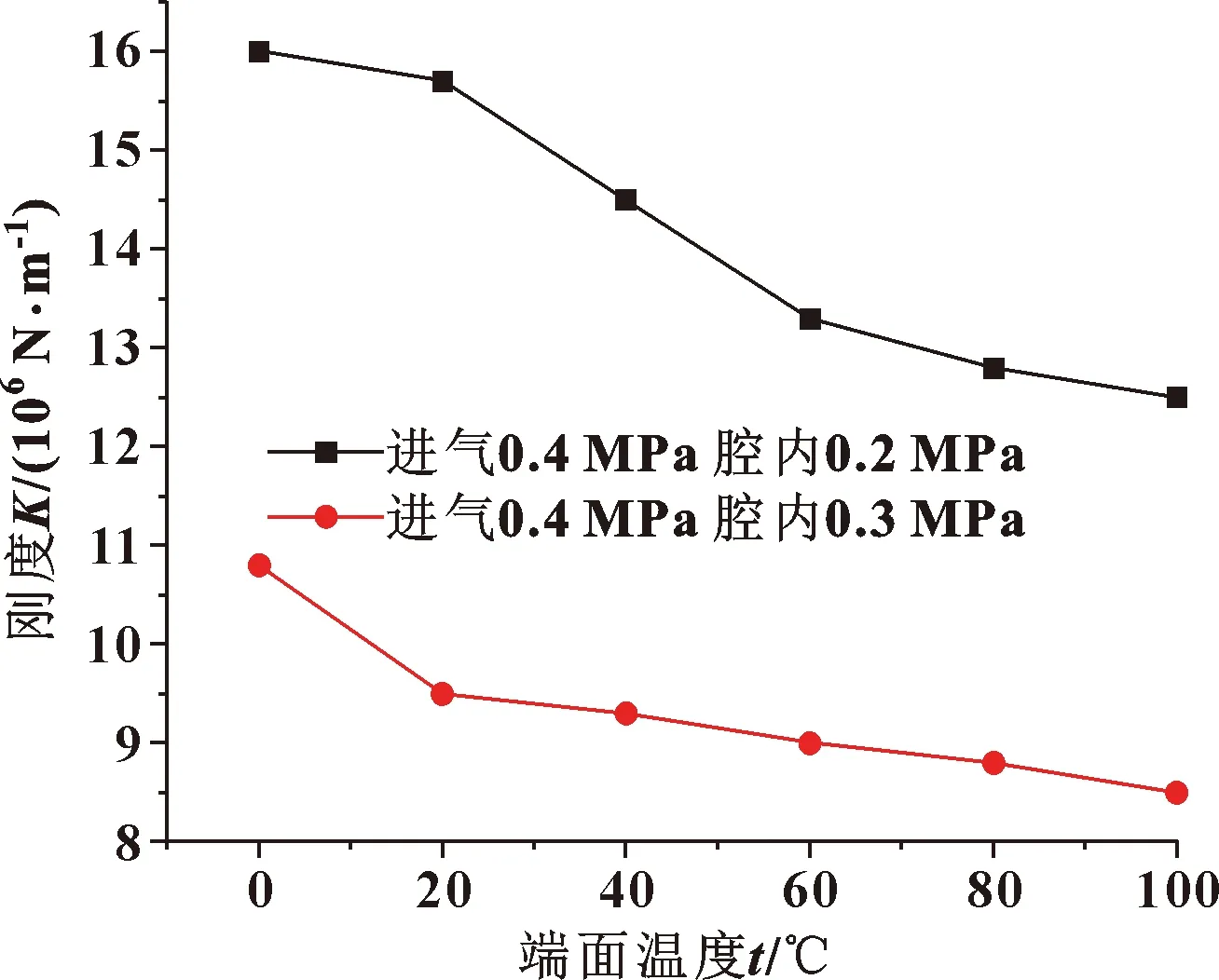
图15 端面温度对气膜刚度的影响

可见，随着端面温度的逐渐升高，密封开启力缓慢上升，而泄漏量和气膜刚度均呈现下降趋势。由于温度对气体性能会产生一定影响，因此会对密封性能产生一定的影响。在实际工程应用中，可以通过调节密封环运行环境的方法控制密封环端面温度，从而使密封环发挥最优密封性能。

5 密封运行状态监测方法

由于异常接触状态下，密封环端面温度比正常工作条件下温度高得多，因此在实际工程应用中可以使用温度监测的方法对密封环的接触状态进行监测，从而保证密封装置平稳运行。

目前针对密封装置的温度测量主要有2种方式，分别是接触式测温与非接触式测温[20]。接触式测温主要是采用热电偶或热电阻等方式进行测量，将热电偶或热电阻埋入密封静环摩擦面一侧，距离端面越近测量越准确。但由于密封环两端面间气膜较小，无法将测温元件贴在其表面进行测温，这是接触式温度测量方法的缺点。非接触式温度测量主要方式有声波测温与红外成像测温。声波测温主要是采取密封端面摩擦所产生的声波，并经过一定处理，得到密封面接触的信息。但是由于静压密封为非接触式密封，密封环在运转时几乎不会接触，且密封运转时噪声较大，如何分辨声波信息目前依旧是一个复杂的问题。红外成像仪能够实现端面温度的连续与实时测量，可以解决高速旋转部件的表面测温问题。红外热成像仪设备简单，操作方便，且测温仪体积较小，可以随时测量与传输温度云图，是目前比较新颖的测量方式，也是一种比较合适的测温方式。

具体监测方法为：通过在腔内腔体上安装红外测温元件，当密封环温度急剧上升且远大于腔内温度时，则可视为密封环损坏。随后通过温度变送器将温度数据信号输送到总控台，并迅速报警。这种方法可以有效增加密封环运行状态的监测效率，为实际工程的安全生产提供一定保障。

为验证可行性，文中搭建了相关试验装置，如图16所示，架设热成像仪在固定位置，通过腔体的视窗进行测温。考虑试验装置实际运转条件与时间成本等多方面因素，文中在不同转速和压力条件下，在运转开始时与运转第5 min时分别对密封环间的缝隙进行温度测量。这样可以初步找到密封环温度变化规律，也可以节约试验时间，提高效率。

图16 试验装置

在1 200 r/min转速条件下，正常工况下试验测量的2组图像如图17所示，异常接触工况试验测量的2组图像如图18所示。可见，经过5 min的运转，正常工况下温升幅度约12%，异常接触工况下温升幅度约为20%。

图17 不同运行时间时热成像温度对比(正常工况)

图18 不同运行时间热成像温度对比(异常接触工况)

由于密封环气膜温度无法直接在运行过程中测量，所以以两环中间缝隙温度为主要测量对象，此处温度视为密封环端面温度。由于试验环境温度变化以及试验自身误差，所以导致数据有一定误差，误差棒图如图19所示。为验证理论值的正确性，将正常工况试验值与理论值进行对比，对比结果如图20所示。可见，试验值变化规律与模拟值规律基本保持一致。

图19 密封环温度变化(误差棒图)

图20 密封环温度变化理论值试验值对比

随后，经过多次在不同转速、不同进气压力下的试验，试验结果如图21所示。由于试验受到多种因素影响，所以密封环温度略有差异，但误差保持在合理范围。将试验数据进行整合，密封环温度试验值变化规律如图21和图22所示。可见，正常工况条件下密封环温升随转速逐渐升高，而异常接触工况下升温幅度明显大于正常工况。

图21 密封环温度变化(异常工况和正常工况)

图22 密封环温度变化(正常工况)

根据模拟及试验数据，在实际工程运行过程中，当密封环温度升温较慢，可视为密封环运行在正常工况条件；相反，当密封环温度急剧增大时，可视为密封环运行于异常接触工况，密封环发生接触摩擦。通过实时监控温升的方法，可以更有效地判定密封环的运行状态，更快速地发现密封环异常运行状态。

6 结论

(1)对于静压式干气密封而言，膜厚增加会使密封环端面温度小幅下降，转速增加会使密封环端面温度大幅升高。

(2)密封环的温度也会受到腔内环境的影响，腔体压力的升高会使密封端面温度缓慢下降，腔体温度的升高会使端面温度缓慢上升。

(3)红外测温装置体积较小，实时传输等特点，可应用于实时监测系统之中。通过实时监控密封环温度的方式，可以实现密封运行状态高效率监控，提高了密封运行的工程应用效率。