主动降噪泄露变步长FxLMS算法研究

百文萌，王劲松，2，高慧杰

（1.长春理工大学 光电工程学院，长春 130022；2.长春理工大学 中山研究院，中山 528437）

主动噪声控制（ANC）是一种利用声波相消干涉原理，人为地产生与噪声同频、等幅、反相的“抗噪声”达到降噪的新技术[1]。在整个ANC系统中，自适应控制算法可以称之为其核心部分[2-3]，其中以计算量小和容易实现为优点的滤波-x最小均方（FxLMS）算法在主动降噪中广泛应用[4]。在FxLMS中，一个不可忽视的存在即为步长因子，因为它既是决定算法能否收敛的关键因素，也是判断收敛速率和稳态误差大小的重要因素。所以，对于FxLMS算法的改进始终是个热门课题。改进的主要目的是在算法收敛的情况下，提高算法迭代过程的收敛速率、降低稳态误差以及有利于算法的硬件实现。目前比较经典的改进算法有归一化LMS算法、泄露FxLMS算法等。其中，虽然归一化LMS算法的收敛速率确有改善，但是在算法稳定后，步长因子不能达到一个较小的值，致使稳态误差较大；泄露FxLMS算法是加入泄露因子可以约束次级信号，降低FxLMS算法不稳定的机会，但是收敛速度没有得到明显的改善。

针对上述步长调整原则和变步长算法的优缺点，提出一种泄露变步长的FxLMS算法来克服传统固定步长的缺点，提高算法的稳定性。本文将对FxLMS算法和改进后的算法分别进行仿真分析，并最终将其运用在双通道主动噪声控制的结构中，以提高降噪效果。

1 噪声主动控制算法的基本原理

FxLMS算法是在最小均方（LMS）算法的基础上考虑到了次级路径存在的影响，由Morgan、Widrow和Burgess独立推导得到[5-6]。前馈单通道FxLMS算法如图1所示，x(n)为输入的初始信号，d(n)为初始信号通过初级传递函数P(z)到达误差传感器附近的期望信号，e(n)为误差传感器接收到的误差信号，W(z)代表自适应滤波器。r(n)是x(n)经过次级路径传递函数估计Ŝ(z)后的滤波信号，将r(n)和e(n)共同作为控制器W(z)的另一个输入信号，通过算法处理后获得的控制器输出信号y(n)再通过次级路径传递函数S(z)可在误差传感器附近得到一个与期望信号相抵消的控制信号yp(n)，从而达到降噪的目的。

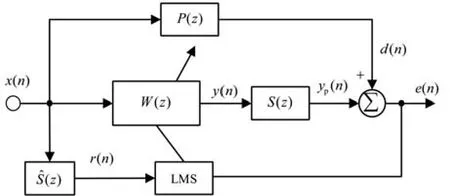
图1 基于FxLMS算法的ANC系统框图

设滤波器的长度为L，其算法具体如下：

（1）某一时间初始信号的输入为：

（2）x(n)经过W(z)后的信号y(n)为：

（3）y(n)经过次级路径后输出的控制信号yp(n)为：

（4）x(n)经过后输出的滤波信号为：

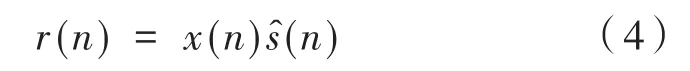
（5）误差传感器处的误差信号为：

（6）通过迭代求取新的滤波器抽头系数：

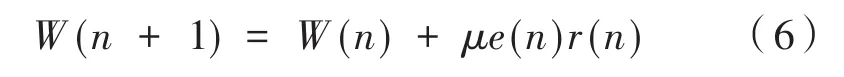
式中，步长μ为一个固定值，取值需满足：

式中，λmax是初始信号向量自相关矩阵的最大特征值。

由上述的公式可知算法的收敛系数μ是一个固定的值，其取值的大小影响着算法收敛速度和系统的稳定性。经过仿真分析可得，步长取值较大时，可使算法较快收敛，但同时会使系统的稳态误差增大，严重时会导致算法发散，步长取值较小时，可使算法的稳态误差较小，使系统的稳定性更好，但是算法达到稳定时所需的时间较长。

2 改进的FxLMS算法

分析可知，步长是一个至关重要的存在，为了更好地兼顾收敛速度和稳态误差这两个关键因素，人们提出了变步长的改进思路[7]，即：在算法初期，为了保证有较高的收敛速率，应使步长因子的值处于一个较大的值，在算法末期，为了保证有较低的稳态误差，则此时对应的步长因子的值也应该较小。在上述的步长设计思路下，考虑到权系数更新过程中由实际次级路径下的数模转换过程产生的量化误差给系统带来的泄露影响[8]，进而提出一种泄露变步长FxLMS算法。

2.1 归一化FxLMS算法

由前文可知，FxLMS算法的权矢量迭代公式为：

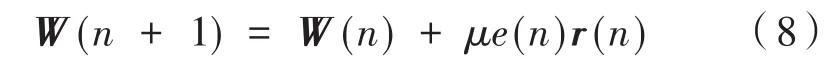
根据归一化FxLMS算法可得步长因子公式为：

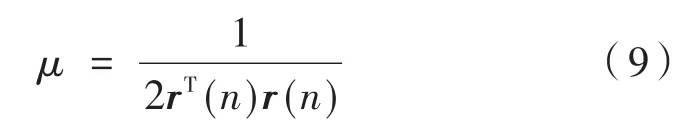
则权系数更新公式改写成：

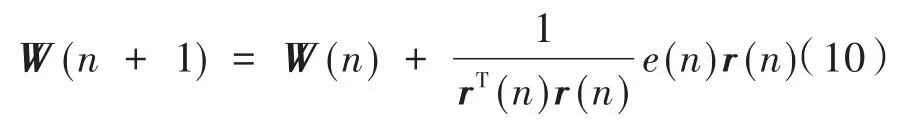
则更为可靠的实现方式[9]为：

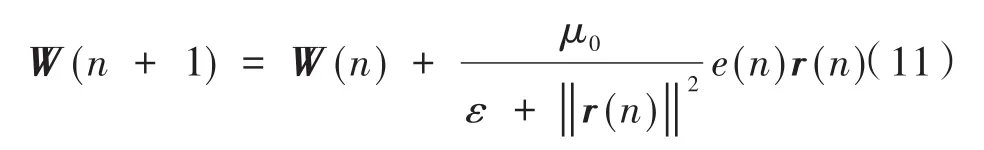
式中，μ0和ε均为正常数。当欧式范数平方‖r(n)‖2出现较小值时，易引起步长过大，从而导致算法发散，常数ε的存在则避免了此类情况的出现。对于存在的常数μ0，可以看作为步长参数，用来控制调节算法的收敛速率和失调量，当μ0=1和ε=0时，此时的递推方程式（11）即为式（10）。

2.2 改进的FxLMS算法

由式（11）可得步长因子与输入的初始信号的自相关矩阵有关。对算法的分析可知，此归一化FxLMS算法的步长因子虽在自适应过程初始阶段有变化，但在自适应过程趋于稳定之后其步长不能达到一个小的值，则稳态误差会增大。在此基础上改变步长，可用步长因子除以误差向量的欧式平方范数，使步长在自适应过程初始阶段有一个较大的值，且伴随着迭代过程的进行，步长也将逐步降低，并最终稳定在一个较小的值，即降低稳态误差，使系统更加稳定。有：

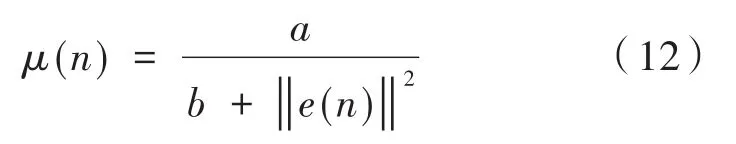
式中，误差向量e(n)的欧式平方范数可以写为，随着采样次数的增加可知，步长μ(n)既和当前的误差量e(n)有关，又和误差向量迭代过程的前n步有关，因此，迭代步长是平滑下降的一个函数[10]，确保了步长在自适应过程的初期值较大，末期值较小，可以有效地降低稳态误差。另外，固定参数a的选取影响着μ(n)的变化，受初始信号的影响，参数值不容易确定。由于此算法中μ(n)的值只能是不断地下降，所以在应对非平稳随机过程系统中的跟踪能力较弱[11]。为此，可引入对数函数对其进行改进，使得μ(n)的值在一定的范围内不断地进行调整，有：

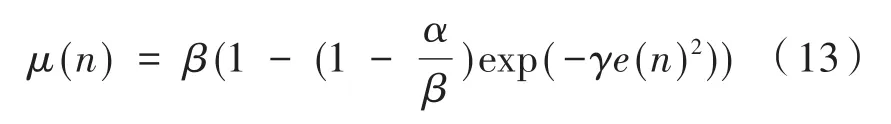
其中，γ的数值影响步长函数μ(n)的陡峭化程度，γ的值越大，其整体的变化率就越快，α和β的值确定了μ(n)的变化范围。这里的e(n)2代表第n次迭代中瞬时误差量的平方值，对比上式e(n)的欧式平方范数而言，运算量大幅度降低，只需要一个标量的平方运算，更易于硬件的实现，并且由于μ(n)仅与当前误差向量e(n)有关，不是单纯地不断下降，而是根据当前的误差在范围内不断地调整，提高了算法的实时性，使算法也适合于非平稳过程。

此时的权系数更新公式为：

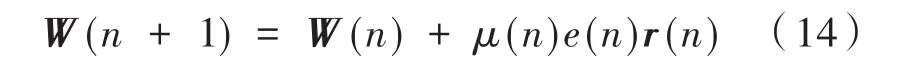
本文提出的泄露变步长FxLMS是在式（14）的基础上，考虑了实际数模转换过程中量化误差带来的泄露影响，可将上式的权值更新公式改写为：

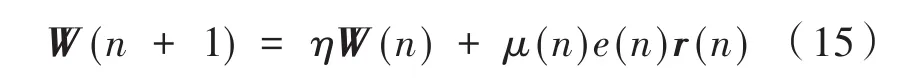
式中，η是泄露系数，是小于且接近1的一个常数。

2.3 次级通道辨识

由前面的分析可知，在更新滤波器抽头系数的迭代公式中含有滤波-x信号矢量r(n)，r(n)是x(n)通过传递函数估计模型求得。对次级路径建模，如图2所示，选择LMS算法模块，获得传递函数估计模型的值。

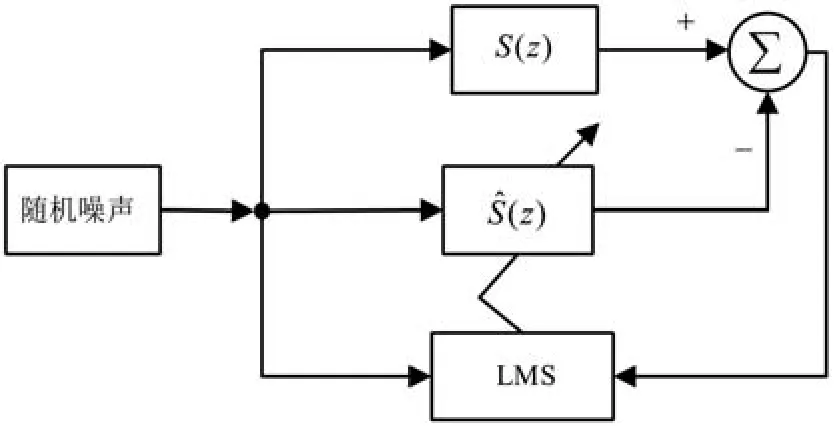
图2 次级通道建模原理图

次级路径建模的步骤如下：

（2）使用误差传感器接收由扬声器产生的对消信号y(n)：

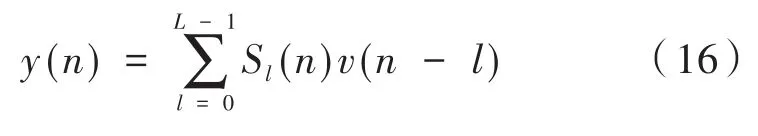
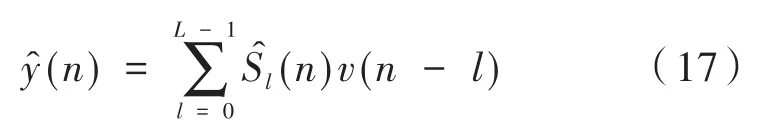
（4）计算路径的实际模型和估计模型之间的输出差值：

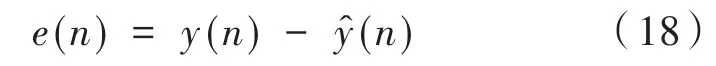
（6）重复以上迭代过程，利用误差信号e(n)不断调节权系数，直至达到设定要求为止，同时将得到的的系数值存储起来，方便后续Fx-LMS算法使用。

现根据图2所示的过程进行次级路径建模仿真，为了验证结果的有效性，设传递函数[12]为：

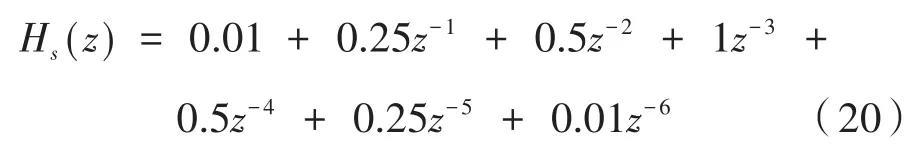
通过对其进行建模分析，取μ=0.01作为建模过程中LMS算法的步长因子的值，仿真的结果如图3所示，从图3（a）中可看出，识别误差从采样点数100往后接近于零，系统也趋于收敛。即建模仿真实验对次级路径的识别效果是稳定的。另外，通过仿真建模实验得到的实际路径和估计路径的滤波器权值也非常接近，仿真结果表明实验有良好的估计值，辨识结果准确。

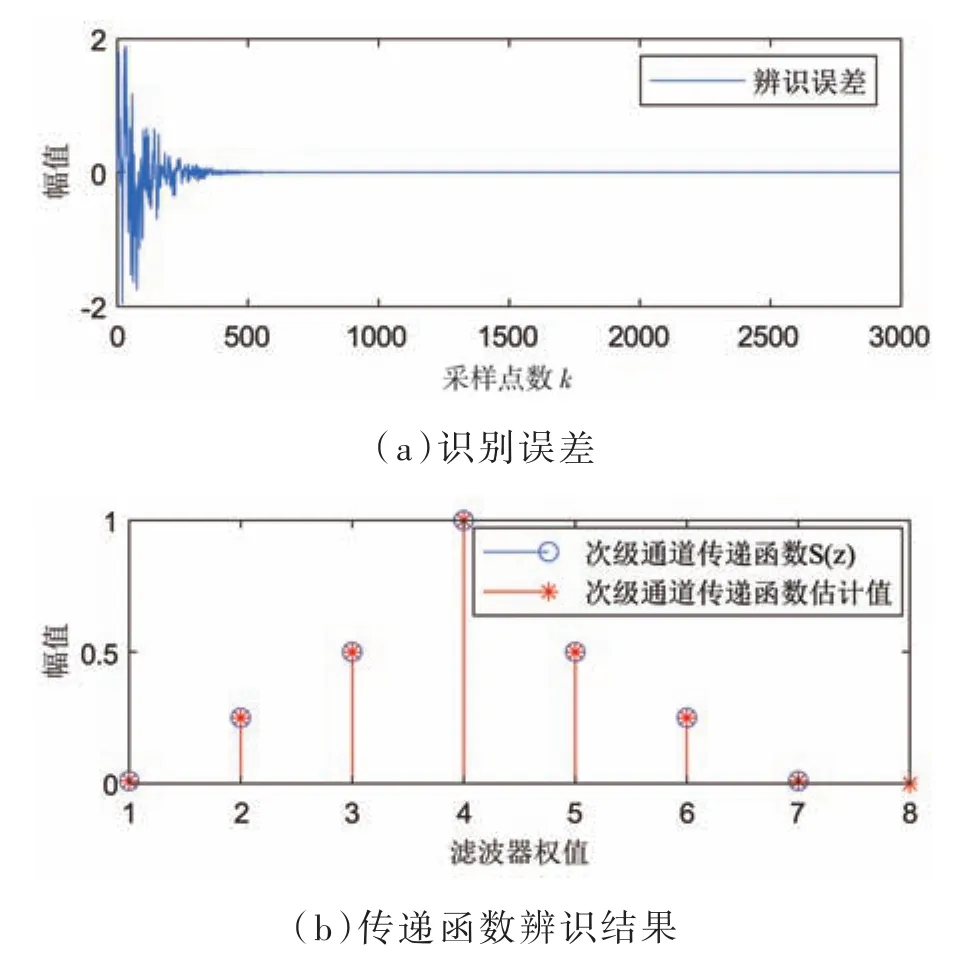
图3 次级通道传递函数建模仿真实验

2.4 改进FxLMS算法的仿真分析

仿真中，将传统的FxLMS算法和本文的改进FxLMS算法进行比较，由于单一的频率信号在实际应用中很少存在，而更常见的是带有一定带宽的噪声信号，因此本文的仿真实验中采用的是混合信号，将x(t)=s(t)+v(t)作为输入信号，其中v(t)是信噪比SNR=7的随机白噪声，s(t)是一个混频信号，则：

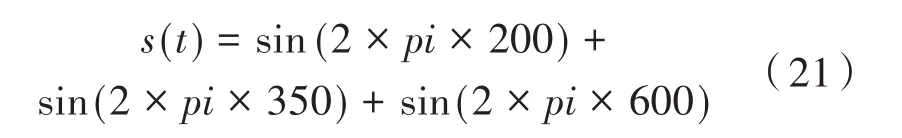
即该信号由频率分别为200 Hz、350 Hz和600 Hz组合构成。考虑到收敛速度和实现的硬件成本，选取滤波器的阶数为16，传统FxLMS算法的固定步长取μ=0.012，改进算法仿真中取泄露因子η=0.999，步长函数各参数取β=0.012，α=0.003，γ值的大小决定其变化率，这里取γ=10。

仿真结果如图4所示，图4（a）和图4（b）分别代表了FxLMS算法和泄露变步长FxLMS算法滤波的噪声残留。从图中可知，噪声经过这两种算法的处理都得到了显著的改善，然而对比观察即可发现，在改进算法的处理下，噪声残留明显有所降低，这是由于改进算法的步长是根据当前误差向量在一定的范围内不断地进行调整，如图4（c）所示，步长在迭代的过程中整体呈现下降的趋势，并且在迭代的后期也处于较小值的状态，因此，收敛后的稳态误差较小，噪声残留也更低。

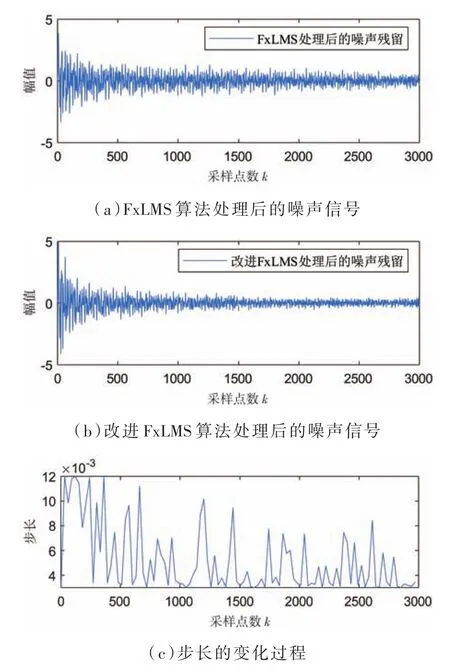
图4 单通道两种算法的仿真结果

为了验证改进算法的优良性，把白噪声作为输入信号，对比FxLMS算法和改进的FxLMS算法的收敛性能，算法的各参数设定值不变，其均方误差（MSE）如图5所示，可以看出改进的FxLMS算法明显比传统的FxLMS算法的收敛速度快，且稳态误差值也较低，整体的稳定性也更好。

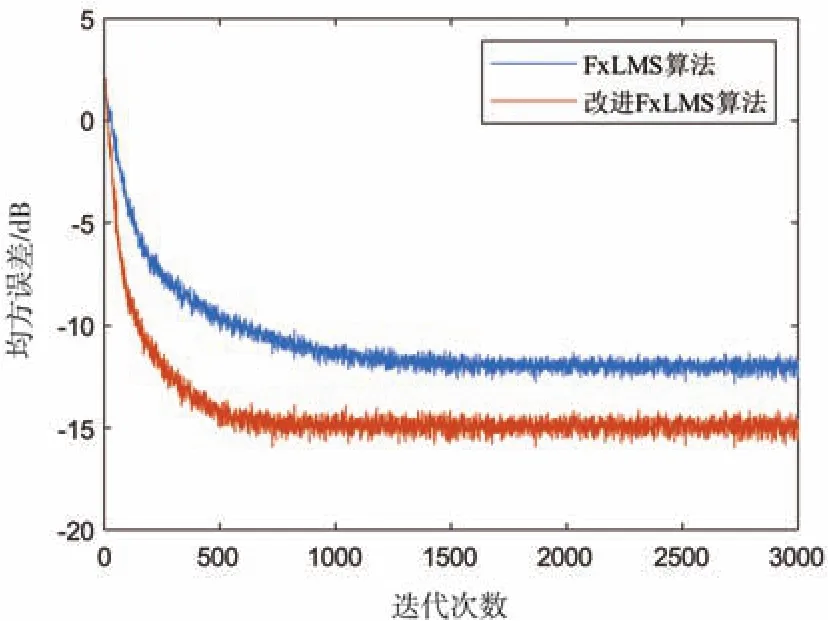
图5 不同算法的MSE对比图

图6为单通道系统下不同算法处理后的功率谱。图6（a）为经过传统FxLMS算法降噪处理后的功率谱，其在中心频率200 Hz、350 Hz、600 Hz处的幅值下降为13.8 dB。图6（b）为提出的泄露变步长FxLMS算法经过降噪处理后的功率谱，其在中心频率处的幅值下降为19.6 dB。

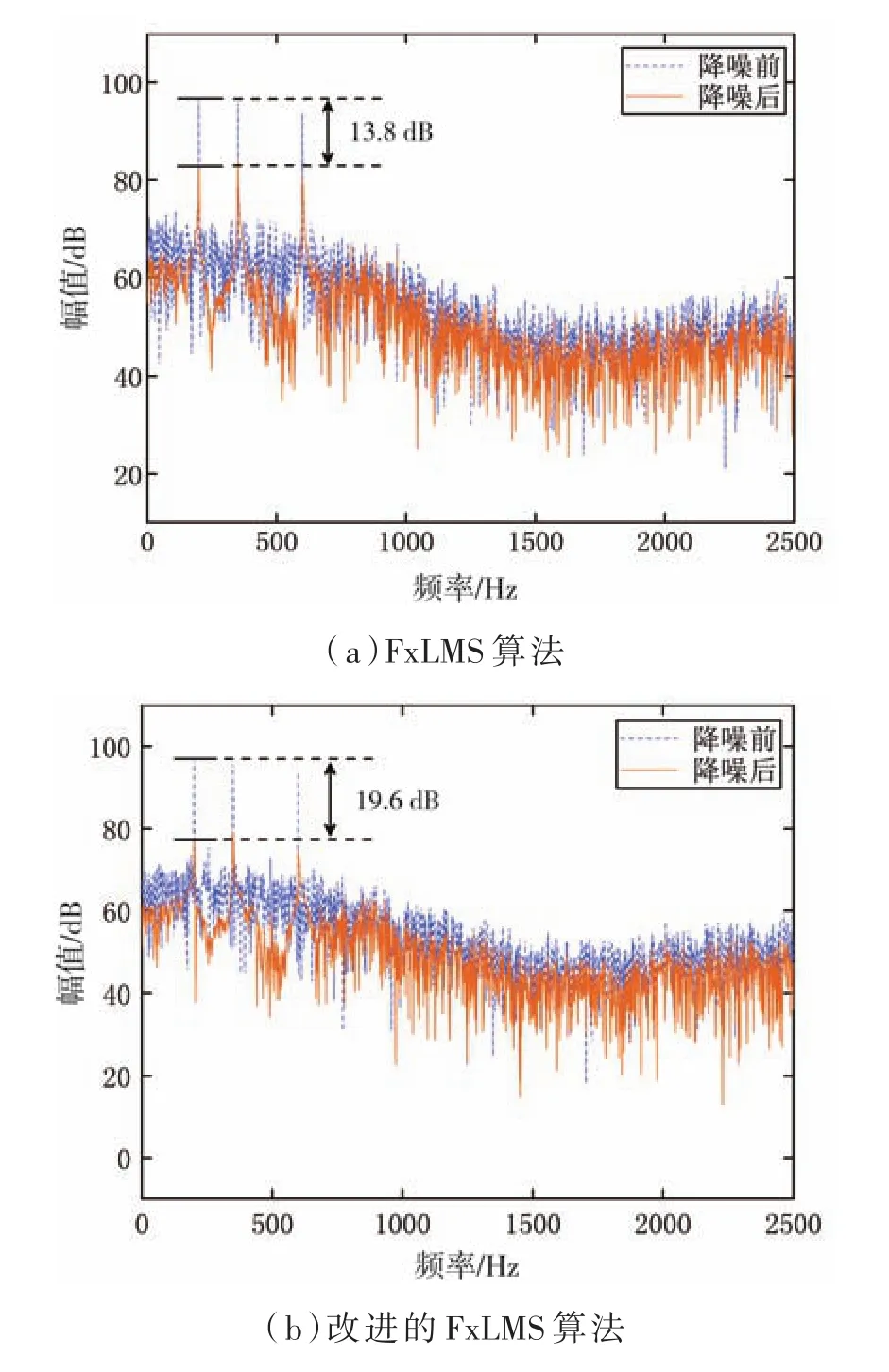
图6 不同算法降噪前后的功率谱

3 多通道ANC系统

由于单通道的ANC系统的降噪范围有限，只能实现小范围内的噪声减小，而有源噪声控制的目的是提高降噪效果，扩大降噪范围以及适应复杂的环境，因此引入多通道控制系统进行降噪。多通道ANC系统与单通ANC系统类似[13]，有I个初始传感器、J个次级声源以及K个误差传感器、因此就存留了I×J个初级通道和J×K个次级通道。

本文将以1×2×2的双通道有源降噪系统为模型，将分别对前文的FxLMS算法和改进的Fx-LMS算法进行分析和对比。

3.1 双通道FxLMS算法

从以上分析可知，双通道的系统模型1×2×2中，包含1×2个初级声通道和2×2个次级声通道，其示意图[14]如图7所示。P1(z)和P2(z)分别代表了初级传感器到误差传感器1和误差传感器2的声通道的传递函数，同理，S11(z)和S12(z)代表的是次级声源1分别到误差传感器1和误差传感器2的次级路径传递函数，S21(z)和S22(z)代表的是次级声源2分别到两个误差传感器的次级路径传递函数。

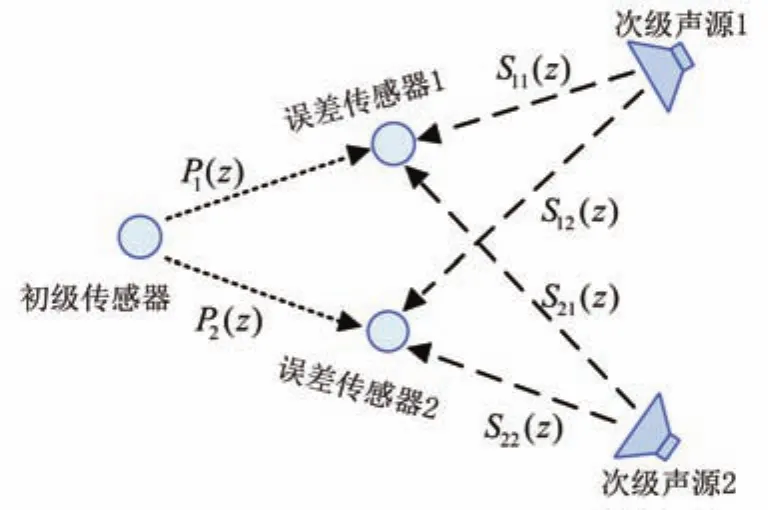
图7 双通道系统示意图

图8为基于 FxLMS算法的 1×2×2结构图，图中有只有一路的信号输入，两路次级信号的输出和四路的次级通道，另外控制器的输入信号是初始信号与四路次级通道传递函数估计值卷积运算后的信号，根据前文的单通道FxLMS算法的迭代过程可以写出这个结构图中的两路误差信号为：

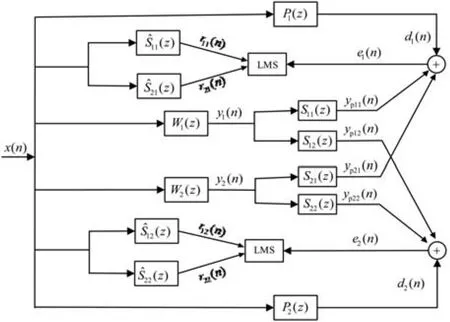
图8 基于FxLMS算法的1×2×2结构图

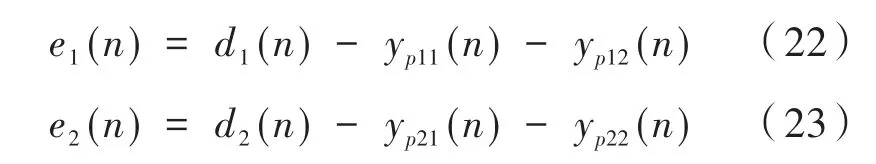
则两个控制器权系数迭代公式为

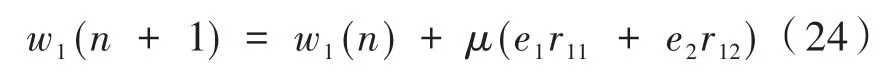
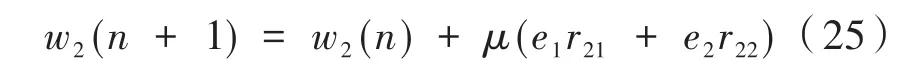
由式（24）和式（25）可知，在权系数迭代更新中每一个控制器都有两个误差量来共同调节，以此达到更好的降噪效果。

3.2 双通道离线建模

双通道系统与单通道系统相比，其系统的复杂度有所增加，如若采用在线建模的方式，稍有不慎就会造成整个系统的发散，此时离线建模的优点将更明显地显现出来，与在线建模相比，其算法的计算量大大减小，算法整体的运行速度和收敛收率也显著提升，且有效地提高系统的稳定性。由于白噪声的各频段分量都是恒定的，因而它对次级通道进行建模而言是一种理想的激励信号，并将获得的次级通道估计值用于后续算法之中。

已知多通道系统中存留J×K个次级通道。而需要采用的FxLMS算法由于滤波信号的存在，则要求对所有的次级通道进行补偿。因此离线建模需要的次级通道估计模型Ŝjk(z)也为J×K个。图9给出了当J=2、K=2时的离线辨识算法结构[15]。

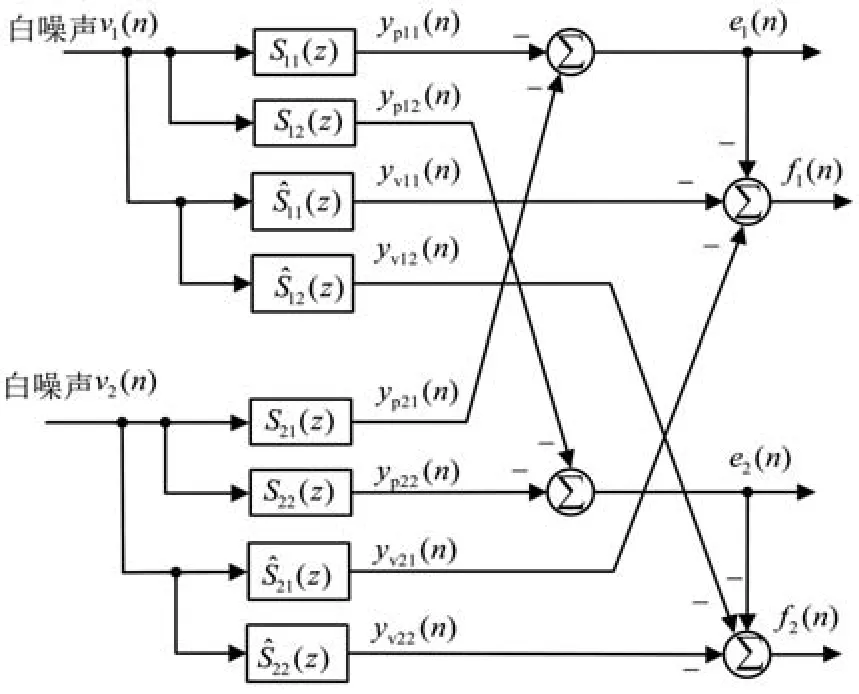
图9 双通道系统次级通道建模原理图

其中v1(n)和v2(n)为双通道离线建模系统输入的白噪声信号，另外，v1(n)、v2(n)经过次级通道估计模型Ŝjk(n)后输出yvjk(n)，而v1(n)、v2(n)经过实际次级通道可输出ypjk(n)，在误差传感器1和误差传感器2位置处，以上两种次级声源叠加可分别构成误差信号e1(n)和e2(n)，其表达有：

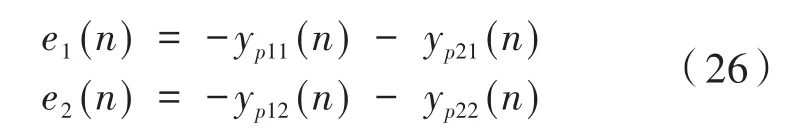
图9中的f1(n)、f2(n)表示输入信号经过次级通道和次级通道估计模型后输出信号之间的差值，即：

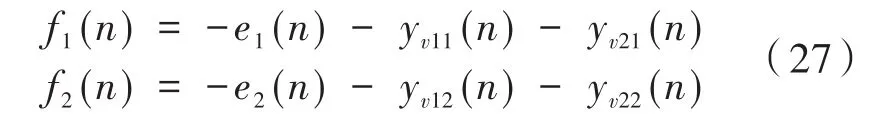
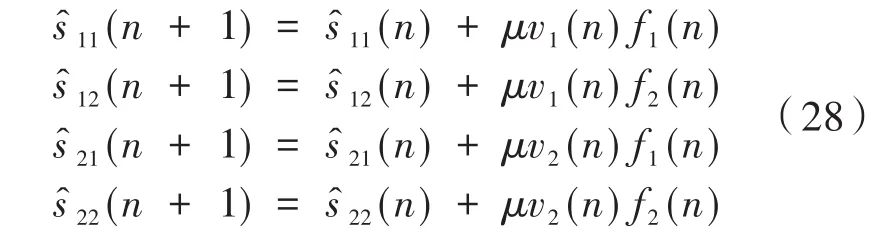
3.3 双通道FxLMS仿真

（1）双通道次级通路建模

在进行仿真前，需要完成上述原理图中所有次级通道传递函的估计，根据文献[16]，可设系统声通道的传递函数，有：

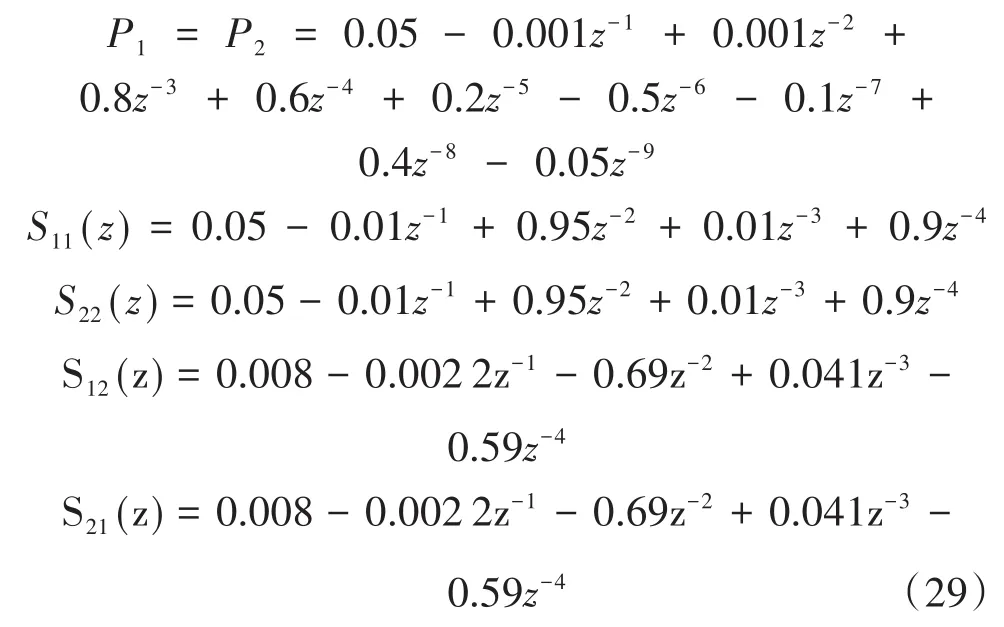
利用本节提及的白噪声来检验上述次级通道传递函数的可行性，其中建模过程中算法的步长因子同样为0.01，以次级通道1为例，其结果如图10所示，即误差信号可以很快地收敛于零，证明了所设置的次级通道传递函数是有效的，且不会造成系统的发散。

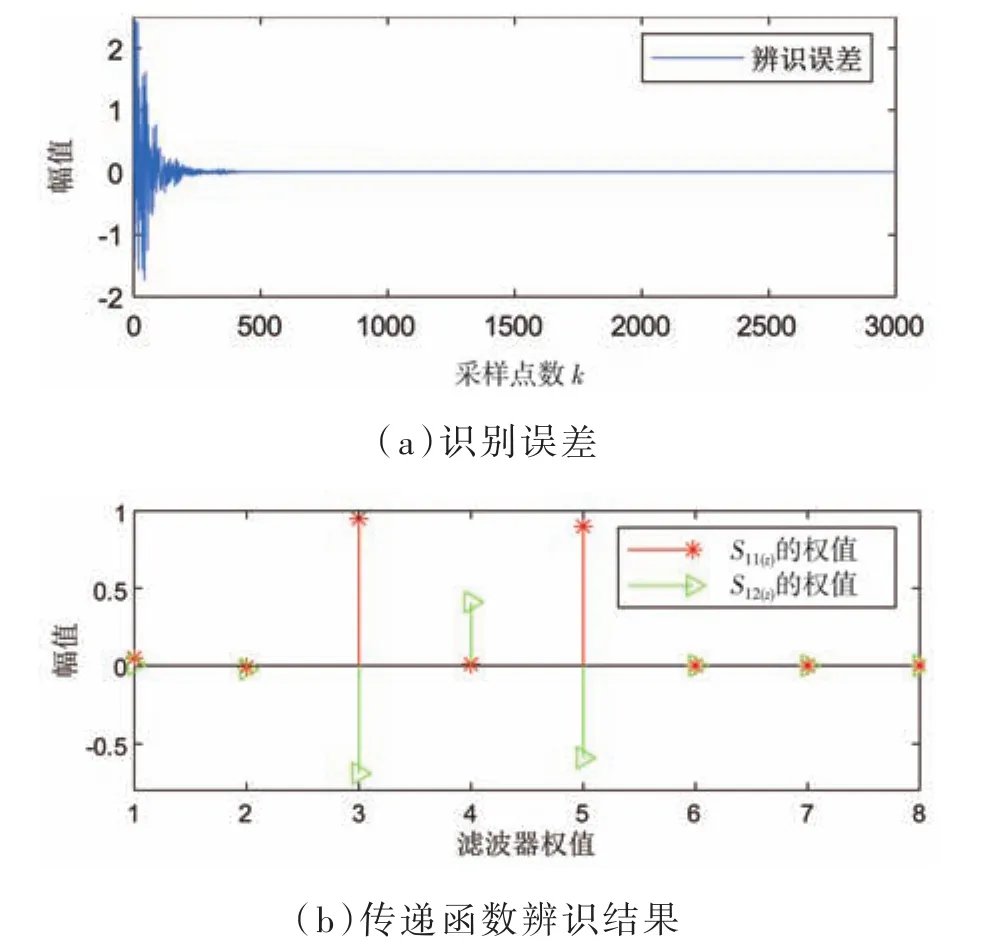
图10 次级通路建模结果

（2）双通道FxLMS算法仿真

仿真的信号参数和前文的单通道的参数一样，则实验仿真结果如图11（a）和图11（b）所示，在双通道中，改进的FxLMS算法仍旧比传统的FxLMS算法的收敛速度更快。

图11 双通道两种算法的仿真结果

图12是两种算法在双通道系统中降噪前后的功率谱。由图12（a）图可得，传统FxLMS算法在降噪前后位于其中心频率的降噪量达到为18.2 dB，由图12（b）知，本文提出的泄露变步长FxLMS算法降噪前后在中心频率处的降噪量最高达到24.7 dB。即双通道比单通道的降噪效果好，且基于改进算法的降噪效果比传统的FxLMS算法降噪效果好。

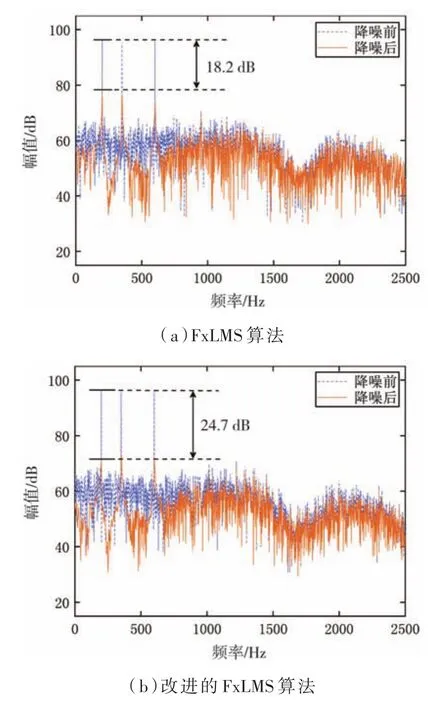
图12 双通道不同算法降噪前后的功率谱

4 结论

本文提出的泄露变步长FxLMS算法以瞬时误差向量的平方值作为步长的函数的输入信号，经仿真结果表明，在收敛速度和稳态误差上均有明显的优势，并且其仿真功率谱表明，经过FxLMS算法和泄露变步长FxLMS算法降噪处理后，在单通道中的降噪量分别为13.8 dB和19.6 dB，而在双通道中的降噪量分别为18.2 dB和24.7 dB，从双通道ANC系统的降噪量可以表明多通道ANC系统有非常好的降噪效果。但是，对于多通道ANC系统而言计算量是未来进一步需要研究的重点。