巧用“一线三等角”模型 突破几何压轴难题
⦿无锡市华庄中学 刘 敏
1 引出问题
2022年安徽中考试题中有这样一道试题:如图1,四边形ABCD是正方形,点E在边AD上,△BEF是以E为直角顶点的等腰直角三角形,EF,BF分别交CD于点M,N,过点F作AD的垂线交AD的延长线于点G.连接DF,则∠FDG=______°.
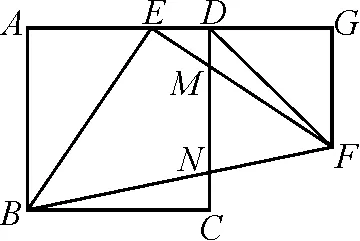
图1
根据题意可以发现,在直线AD上,存在三个直角,∠A=∠BEF=∠G(或者∠A=∠BEF=∠EDM),出现这种情况,我们往往称之为“一线三直角”的数学模型,从而利用两个三角形全等或者相似即可.此题可根据“AAS”证△ABE≌△GEF,得出EG=AB,GF=AE,进而推出DG=GF.即可得出∠FDG的度数.
若将“一线三直角”模型中的直角改为其他角度,这样就形成了“一线三等角”的数学模型,在解答相关问题的过程中,很容易考虑到全等三角形或者相似三角形的判定.熟练把握“一线三等角”的相关特点,感悟其在全等或者相似三角形判定中的重要作用,便于引导学生在解答过程中快速掌握利用基本图形来描述或者分析、解决问题,从而培养学生的几何直观能力.
2 “一线三等角”在全等形问题中的应用
例1阅读下面的相关材料,并回答问题.
模型学习:如图2,∠BAD=90°,AB=AD,BC⊥AC于点C,DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D;又∠ACB=∠AED=90°,可以通过推理得到△ABC≌△DAE,进而得到AC=______,BC=______.我们把这个数学模型称为“一线三等角”模型.
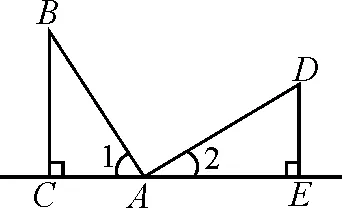
图2
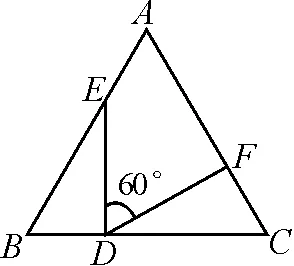
图3
模型应用:如图3,△ABC为等边三角形,BD=CF,∠EDF=60°,求证BE=CD.
在“模型学习”中根据这种模型的特点,可以直接判断,由“AAS”可证△ABC≌△DAE,可得AC=DE,BC=AE;对于“模型应用”,根据条件可以发现∠B=∠C=∠EDF=60°,符合“一线三等角”的特征,故由“AAS”可证△BDE≌△CFD,从而可证明得到BE=CD.
3 “一线三等角”在相似形问题中的应用
例2如图4,D为△ABC的内心,点E在AC上,且AD⊥DE,若DE=2,AD=CE=3,试求AB的长.
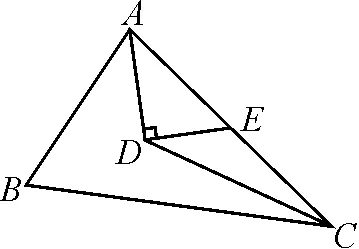
图4
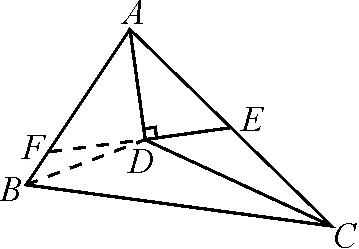
图5
通过审题发现,题干中有内心,还有垂直,问题的目标AB与条件AD,CE分属三条直线.因此可以考虑延长DE看是否可以构建“一线三等角”.于是延长ED交AB于点F,连接BD,如图5,将线段AB分为AF和BF两部分,分别计算.显然,根据条件很容易证明△ADE≌△ADF,利用勾股定理求得AE的长度,即为AF的长度.再根据△ADE≌△ADF,可以得到∠AFD=∠AED,故有∠BFD=∠CED.利用三角形内角和可推理计算得到∠ABD=∠CBD=∠CDE,从而可得到△BFD∽△DEC,再利用相似,列比例式求得BF.BF与AF相加即可求得AB.
4 “一线三等角”在一次函数中的应用
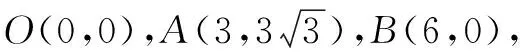

图6
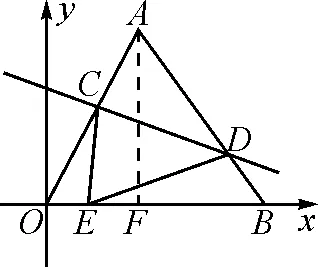
图7

5 “一线三等角”在反比例函数中的应用
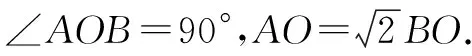
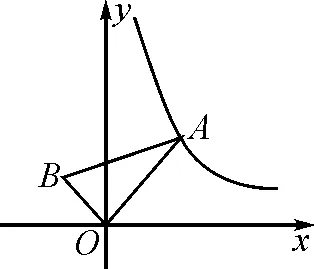
图8
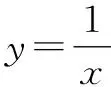
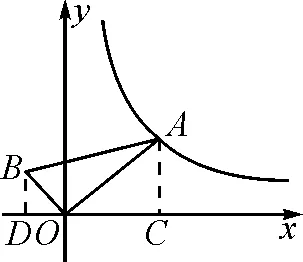
图9
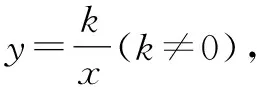
6 “一线三等角”在二次函数中的应用
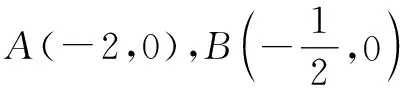
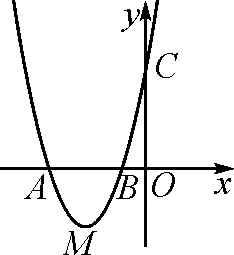
图10
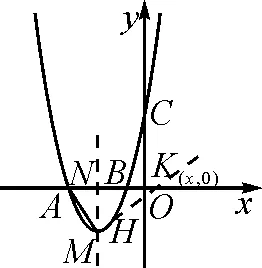
图11
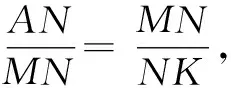
再如:如图12所示,抛物线y=ax2+bx+4过A(2,0),B(4,0)两点,交y轴于点C,过点C作x轴的平行线与抛物线的另一个交点为D,连接AC,BC.点P是该抛物线上一动点,设点P的横坐标为m(m>4).若∠ACP=45°,求m的值.
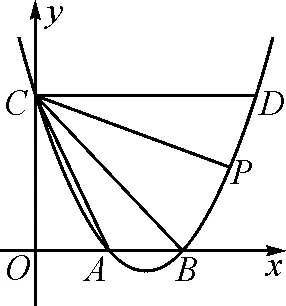
图12

图13
对于此题,我们也是很难快速确定点P的位置,为此可以利用“一线三等角”模型,过点A作AC的垂线AE,并使得AE=AC,如图13,易得点E的坐标.连接FC,交抛物线于点P,将直线EC的解析式代入抛物线求得交点坐标,即可求得除点C外的另一交点P,思路清晰,方法简单,问题迎刃而解.
7 “一线三等角”在图形变换中的应用
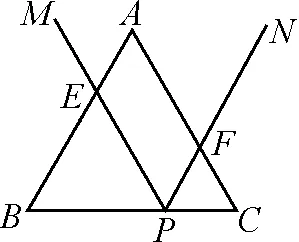
图14
例6等边△ABC边长为6,P为BC边上一点,∠MPN=60°,且PM,PN分别于边AB,AC交于点E,F.如图14所示,若点P在BC边上运动,且∠MPN绕点P旋转,当CF=AE=2时,求PE的长.
根据题意,△ABC是等边三角形,∠MPN=60°,可知∠B=∠C=∠MPN,符合“一线三等角”模型.因此可以考虑使用该模型下的解题基本思路.通过证明△BPE∽△CFP,根据相似三角形对应边的比相等,再设BP=x,则CP=6-x,即可求得BP的长,进而求得PE的长.
8 “一线三等角”在动态问题中的应用
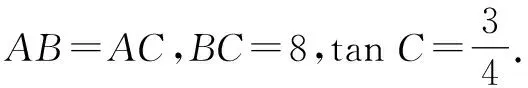
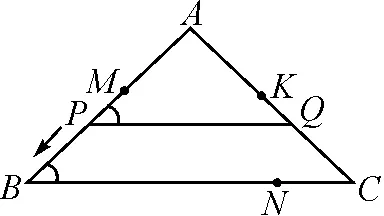
图15
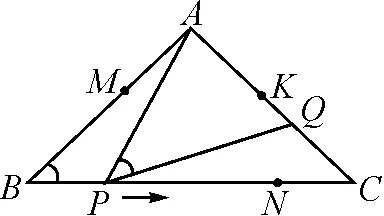
图16
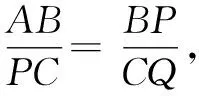
通过上述问题的研究,可以感受“一线三等角”模型在各个知识背景下的应用.借助构造一线三等角模型解题的基本手段,从复杂的图形中分离出基本图形,具有将问题化繁为简的效果,同时可以帮助我们在解题中快速找到解决问题的突破口.当然,希望“一线三等角”模型能起到抛砖引玉的作用,更希望学生能形成比较完善的知识储备,从而提高基本图形的敏锐观察力,以及不断提升几何直观能力和问题建模思想.Z

