视场角受限的三维攻击角度控制导引律

陈亚东，王琭珉，郭大庆，刘俊辉，王佳楠

(1.北京理工大学宇航学院，北京 100081；2.北京宇航系统工程研究所，北京100076)

0 引 言

有关攻击角度控制问题的研究从20世纪70年代便已经开始，而且随着实际应用的牵引和理论研究的深入，越来越多的约束引入到制导律设计中。Kim等[1]设计了一种用于再入飞行器的次优末端姿态角控制制导方法，在攻角为小角度的情况下，可将该方法应用于攻击角度控制。随着精确制导技术的发展，制导弹药被广泛用于反坦克和反舰船等场景。由于坦克和舰船防护的升级，进攻方需要采用具有攻击角度控制能力的制导方法以提高导弹的穿甲能力。York等[2]在文献[1]的基础上进一步考虑了小攻角假设以及自驾仪响应时间对落角约束制导方法的影响。Ryoo等[3]采用线性化制导模型结合线性系统最优控制理论提出了考虑一阶、二阶自驾仪特性的最优攻击角度约束制导方法，同时给出了剩余攻击时间估算方法。Shaferman等[4]则基于线性化制导模型提出了一种线性二次型最优攻击角度制导方法。刘丹等[5]提出了一种具有攻击角度约束的最优制导方法。Ratnoo等[6]提出了一种基于状态依赖黎卡提方程(State-dependent riccati equation，SDRE)的次优落角约束制导方法。刘俊辉等[7]考虑脉冲力控制形式特点，基于扩展极大值原理提出了一种带攻击角约束的脉冲式最优制导律。刁兆师等[8]采用反步法提出了一种考虑驾驶仪特性的攻击角度控制方法。孙胜等[9]采用终端滑模控制方法提出了一种考虑驾驶仪动态特性的攻击角度控制方法。除了基于最优控制理论和非线性控制理论等发展而来的攻击角度控制方法，偏置比例导引和弹道成形方法也常用来设计攻击角度控制制导律。Kim等[10]提出了一种偏置比例导引来实现比例导引的攻击角度控制。Ratnoo等[11]则通过对比例导引攻击角度的预测和控制实现了平面落角约束制导。Dhabale等[12]还采用了三次多项式弹道成型方法设计了一种针对静止目标的攻击角度约束制导方法。上述方法只考虑了平面攻击角度约束制导问题，而三维攻击角度控制问题则呈现出更为复杂的耦合特性，无法通过平面攻击角度约束制导方法的简单拓展实现，需要进一步的研究。

针对带攻击角约束的三维制导，已有不少研究工作。韩大鹏等[13]运用微分平坦理论设计了三维耦合条件下的多约束制导律。Oza等[14]提出模型预测静态规划(Model predictive static programming，MPSP)方法，实现了三维非线性攻击角度约束制导，考虑了打击静止和机动目标的有推力和无推力导弹制导问题。马培蓓等[15]则对三维制导过程的视线角动力学进行了分析，基于李雅普诺夫稳定性原理设计了一种针对静止目标的三维落角约束制导方法。Lin等[16]则对SDRE在平面和三维攻击角度约束制导中的应用进行了归一化分析。熊少锋等[17]针对大气层内导弹逆轨拦截高速机动目标问题，将三维制导分解为两个相互垂直平面内的二维制导，基于最优控制设计了带角度约束的三维制导律。赖超等[18]对侧滑转弯(STT)导弹的攻击角度约束制导问题进行了研究，提出了一种基于自适应终端滑模动态面控制的三维攻击角度约束部分制导控制一体化方法。梁晨等[19]采用深度强化学习算法提出了一种三维攻击角度约束制导律。Nanavati等[20]通过分析制导过程中速度前置角与攻击角度之间的关系提出了一种三维攻击角度约束制导方法，并验证了该方法在导弹速度变化情况下的制导性能。上述工作对三维攻击角度约束制导问题进行了研究，并获得了一些解决方法。而随着制导技术的发展，制导约束不断耦合，需要进一步考虑多种约束情况下的制导方法。

随着探测器测量性能的提升和捷联制导算法的发展，越来越多导弹采用捷联导引头，尤其是低成本制导弹药，而由于捷联导引头与弹体固连且探测视场有限，所以制导律设计需要考虑制导过程中的视场角受限问题。黄诘等[21]基于比例导引提出了一种具有视场角约束的攻击角度控制方法，通过对偏置项进行三阶段设计，使得制导过程同时满足视场角和过载等约束条件限制。郭佳晖等[22]针对制导炮弹的末制导问题，基于有限时间滑模控制理论设计了一种带有攻击角度和视场角约束的有限时间导引方法，并采用扩展观测器对目标机动进行了补偿。李骁宝等[23]也通过有限时间滑模控制理论设计了一种针对机动目标且视场角受限的攻击角度控制方法。Liu等[24]则提出了一种考虑飞行速度时变和过载饱和的攻击角度和视场角约束制导方法。Kim等[25]则基于比例导引提出了一种具有时变偏置项的攻击角度控制导引律，保证了制导指令的平滑且可满足视场角约束。张道驰等[26]则针对空地导弹进行大落角攻击时由于导引头跟踪误差角过大导致目标丢失的问题，通过对最优弹道成型制导律下导引头跟踪误差角的解析计算，提出了一种满足导引头视场角和落角约束的制导方法。Lee等[27]则对捷联制导弹药视场角受限情况下的攻击角度控制范围进行了研究。何绍溟等[28]则通过滑模控制理论提出了一种具有视场角约束和有限时间收敛特性的鲁棒攻击角度控制方法。上述视场角受限的攻击角度控制方法均为平面制导方法，忽略了三维制导过程中的耦合特性。为进一步提高多约束制导性能，需对视场角受限的三维攻击角度控制方法进行研究。胡庆雷等[29]通过俯仰和偏航通道的三次多项式拟合弹道成型方法提出了一种具有视场角约束的三维解析攻击角度控制方法。Liu等[30]则通过俯仰偏航分通道解耦实现了视场角约束情况下的三维攻击角度控制。

通过文献综述可以发现最初的攻击角度约束制导律大多采用平面制导模型，由于平面攻击角度约束制导问题模型较为简单，可采用最优控制理论、偏置比例导引、滑模控制、SDRE以及弹道成型等多种方法来解决。随着制导问题研究的深入，一些学者对三维攻击角度约束制导问题展开了研究。由于三维攻击角度约束制导问题较为复杂，MPSP、SDRE、自适应终端滑模、强化学习等方法被用于解决该类问题。而随着捷联导引头的普及，视场角约束问题也成为了研究的重点，一些学者对视场角约束下的攻击角度控制问题进行了研究。目前大多数工作都是基于平面制导模型，少数成果中考虑了三维制导问题模型[27-28]。现有视场角受限的三维攻击角度控制导引律中多采用欧拉角坐标转换来描述三维制导问题模型，存在坐标变换的奇异性问题，且制导指令的设计较为复杂，不够直观。本文采用三维矢量制导问题模型，首先结合四元数理论进行三维比例导引攻击角度解析预测。然后设计末端攻击角度变化方式，并利用空间几何关系约束求解期望三维制导指令。进一步通过制导动力学闭环分析校验了制导误差的收敛性和视场角的有界性，并结合闭环制导方程的速度大小无关性证明了导引律对速度变化适应性。最后通过数学仿真校验了算法的正确性和有效性。本文提出的导引律避免了坐标变换奇异性问题，且具有指令可解析计算以及误差反馈闭环动力学简单直观的优点。

1 视场角受限的三维攻击角度控制问题模型

1.1 三维制导模型

考虑如图1所示的三维制导模型，OXIYIZI为惯性系，M为导弹，T为静止目标，R为相对位置矢量，可表示为

R=PT-PM

(1)

式中：PT为目标位置矢量；PM为导弹位置矢量。

假设iI,jI,kI分别为沿惯性系OXIYIZI各轴的单位矢量，Vm,xI,Vm,yI,Vm,zI分别定义为导弹速度矢量Vm沿惯性系OXIYIZI各轴的分量。

图1 三维制导矢量模型Fig.1 Three-dimensional guidance vector model

假设在末制导段飞行速度大小为常值，Am为导弹法向加速度矢量，Ωm为导弹速度矢量的旋转角速度矢量，满足

(2)

式中：vm为导弹速度大小。ΩR为弹目视线的旋转角速度矢量，满足

(3)

式中：r为弹目距离。

1.2 视场角及末端攻击角度约束模型

随着捷联导引探测装置的普及，视场角限制在导弹末制导阶段广泛存在。在小攻角假设下，可认为导引头主轴与速度轴重合，进而可将视场角限制近似为速度前置角σ的约束

σ∈[0,σmax]

(4)

式中：σmax为最大速度前置角；σ定义为飞行速度和弹目连线之间的空间夹角大小，可表示为

(5)

式中：·代表点乘。而在速度大小定常假设下，末端攻击角度约束可表示为

(6)

(7)

图2 期望攻击角度示意图Fig.2 Diagram of desired impact angle

视场角受限的三维攻击角度控制问题可视为在满足约束条件(4)和(6)情况下的目标攻击问题。

2 视场角受限的攻击角度控制方法

2.1 三维比例导引及其末端攻击角度预测

三维比例导引指令为

(8)

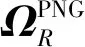
则根据式(2)可得比例导引下的速度矢量旋转角速度为

(9)

由制导指令(8)可以看出导弹始终在速度-弹目连线构成的相对运动平面内机动，因此在比例导引条件下打击静止目标将在初始弹目相对运动平面内完成。

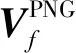
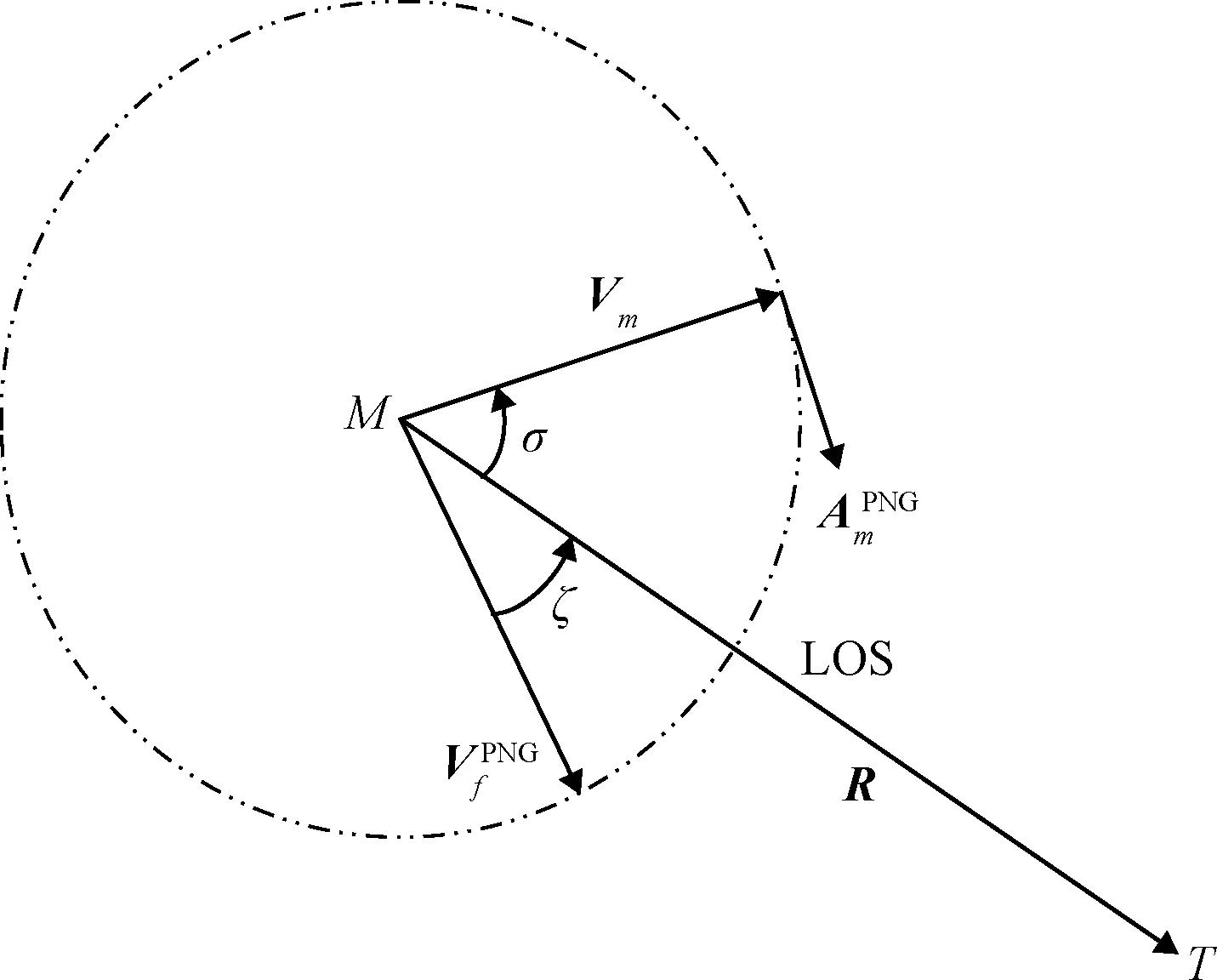
图3 比例导引运动平面Fig.3 Motion plane of PNG

(10)

式中：kL为沿ZL方向的单位矢量，可表示为

(11)

飞行速度矢量的旋转角速度可表示为

(12)

根据式(9)可得

(13)

对上式进行积分可得：

(14)

式中：t0,tf分别为初始和末端时刻。

通过式(14)可得

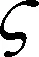
(15)

由于比例导引末端前置角为0，可知

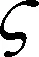
(16)

根据式(15)～(16)可知

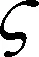
(17)

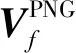
(18)

式中：φ为旋转角度大小，可表示为

(19)

根据四元数理论可知

(20)

式中：

(21)

式中：

(22)

式中：

(23)

通过式(20)可预测比例导引末端速度矢量，即攻击角度。

2.2 三维比例导引攻击角度控制制导指令设计

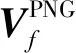
(24)

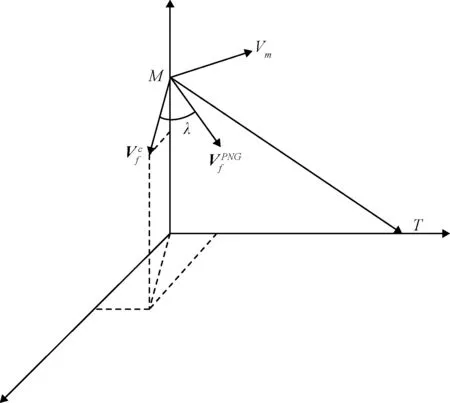
图4 比例导引攻击角度控制示意图Fig.4 Diagram of PNG impact angle control

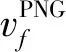
(25)

式中：ka为攻击角度控制增益；kVc是沿MZVc方向的单位矢量且可表示为

(26)

根据式(25)～(26)可得

(27)

图5 制导指令示意图Fig.5 Diagram of guidance commands

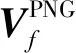
(28)

(29)

式中：AVf可通过ΩVf获得

(30)

(31)

(32)

通过图3可得

(33)

式中：ωr为视线角速率，可表示为

(34)

通过相似的推导可得

(35)

根据式(13)，(33)和(35)可得

(36)

(37)

由于采用了速度大小定常假设，可得

(38)

进而可得攻击角度控制制导指令，即法向加速度指令为

(39)

在导引指令的计算过程中kL和kVc的计算在λ=0或者σ=0时会发生奇异。根据kL的定义可知：在σ=0时可以是垂直于R的任何单位向量，所以当λ≠0而σ=0时，可以认为kL=kVc。相似地当λ=0而σ≠0时，可以认为kVc=kL。当λ=0且σ=0，制导指令应为0，kL和kVc可取任意值。

2.3 制导误差收敛性分析及视场角约束能力分析

根据式(33)和(36)可得

(40)

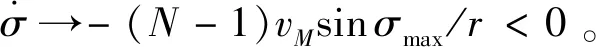
定义李雅普诺夫函数

S=λ2

(41)

对其求导可得

(42)

由于σ∈[0,σmax]，所以有

(43)

且等号仅当σ=σmax时成立。进而可得

(44)

在式(44)中，等号仅当σ=σmax,λ=π或λ=0时成立。由视场角约束能力的分析可知σ=σmax时，制导律趋于比例导引σ=σmax状态无法维持，为不稳定平衡点。由攻击角度误差定义可知λ=π代表期望攻击角度与当前比例导引攻击角度反向，该情况下工程中出现概率极小，且一旦出现扰动系统将脱离该平衡点向λ=0处收敛，该平衡点也为不稳定平衡点。进而可知λ=0为闭环非线性系统的唯一稳定平衡点，因此制导律(39)可保证攻击角度误差的收敛性。进一步，根据式(25)和(40)可知，当λ→0时，偏置项接近于0，制导律趋近于比例导引，从而保证末端σ→0。

2.4 速度大小变化情况下的制导轨迹不变性分析

通过前面的理论推导和分析得到了速度大小定常情况下的导引律，由于本文研究的制导问题打击对象是静止目标，且视场角和攻击角度约束条件也可通过制导轨迹特性得到满足，若能证明在导引律(39)作用下制导闭环动力学在导弹速度大小变化情况下制导轨迹的不变性，则可证明该制导方法对导弹速度大小变化的适应性。

为证明制导闭环动力学在速度大小变化情况下的制导轨迹不变性，定义

(45)

由制导律的设计过程可知

(46)

根据式(36)和(38)进一步可得

(47)

因此导引指令(39)可表示为

(48)

式中：

(49)

根据定义可知

(50)

单位矢量Re和弹目距离的导数为

(51)

(52)

式中：

(53)

式中：Amt和Amn分为切向和法向加速度矢量。则有

(54)

式中：at为轴向加速度大小。进而可得

(55)

由于

vmdt=ds

(56)

式中：s为轨迹长度，进而可得

(57)

由于导弹飞行轨迹可通过R=Rer的变化来确定，结合式(57)可发现导弹飞行轨迹变化的动力学方程中不包含飞行速度大小，即飞行速度大小的变化不会影响飞行轨迹的形状。

3 仿真校验

3.1 制导轨迹的速度大小无关性校验

设置2枚导弹以相同的初始状态攻击位于(0,0,0) km的固定目标，M1速度定常，M2速度变化，制导初始状态为，R=(-10,-10,-10) km,Vm=(-100,-200,-100) m/s。M2切向加速度大小随时间变化规律为

at=5sin(0.1t)

两枚导弹的制导参数为N=3,ka=2。捷联导引头最大视场角为30°。设置攻击角度约束为θc=0°,φc=-90°。仿真结果如图6～9所示。

从仿真结果图6可以看出，两枚导弹具有完全重合的制导轨迹，且均成功命中目标。而从制导状态的时间曲线图7～9可以看出，由于两枚导弹具有不同的速度，制导状态在时间上的变化曲线有所不同。但图8中的攻击角度误差均在末端时刻趋于零，而图9中的速度前置角曲线均收敛至零。此仿真结果可验证制导轨迹与导弹速度大小变化的无关性。

图6 不同速度下制导轨迹Fig.6 Guided trajectories with different speed

图7 不同速度下加速度大小曲线Fig.7 Curves of acceleration with different speed

图8 不同速度下攻击角度误差曲线Fig.8 Curves of impact angle error with different speed

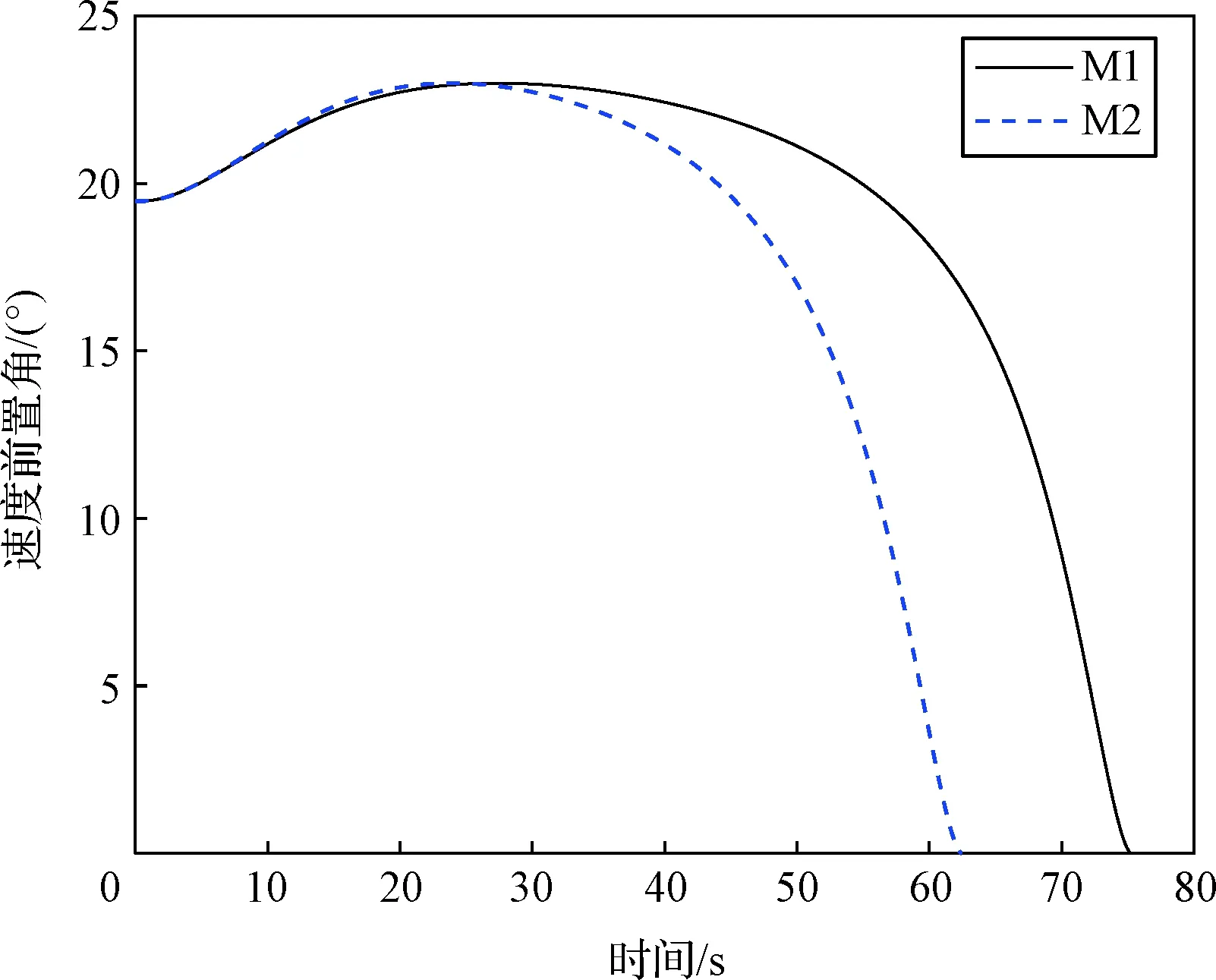
图9 不同速度下前置角曲线Fig.9 Curves of leading angle with different speed

3.2 视场角约束能力校验

由制导指令设计过程可知，制导过程中的视场角约束由系数项cos(πσ/(2σmax))实现，若将该系数项设为1，则制导方法对前置角无限制，成为文献[31]中的控制方法。设置两枚导弹以相同的初始状态攻击位于(0,0,0) km的固定目标，设置制导初始状态为R=(-10,-10,-10) km,Vm=(-100,-200,-100) m/s。假设两弹的最大视场角均为30度，M1采用本文所设计制导方法，M2采用文献[31]中的方法，两枚导弹的制导参数为N=3。设置攻击角度约束为θc=0°,φc=-90°。仿真结果如图10～13所示。

从仿真结果图10中可以看出，两枚导弹具有不同的制导轨迹，但均实现了对目标的击顶打击。图11中的加速度曲线也有较大区别，M1的初始加速度较小而在末端加速度有一个拉升过程，但两枚导弹的加速度最终均趋于零。图12中攻击角度误差曲线显示两枚导弹具有相同的初始攻击角度误差，虽然误差收敛过程有所不同，但最终均趋于零。而图13中的速度前置角曲线则显示，M1的前置角始终满足视场角约束，而M2的视场角则在部分时段超过了视场角限制。仿真结果验证了提出的制导方法在攻击角度控制过程中的视场角限制能力。

图10 视场角约束下制导轨迹Fig.10 Guided trajectories under field-of-view constraint

图11 视场角约束下加速度大小曲线Fig.11 Curves of acceleration under field-of-view constraint

图12 视场角约束下攻击角度误差曲线Fig.12 Curves of impact angle under field-of-view constraint

图13 视场角约束下速度前置角曲线Fig.13 Curves of leading angle under field-of-view constraint

3.3 大范围攻击角度控制能力校验

为验证所提制导算法的大范围攻击角度控制能力，本场景将设置多种攻击角度来对制导算法进行验证。设定目标位置(0,0,0) km，导弹初始状态为R=(-10,-10,-10) km,Vm=(-100,-150,50) m/s。视场角限制为60°，制导参数为N=3,ka=6。设置不同的攻击角度约束如表1。不同攻击角度约束条件下的仿真结果如图14～17所示。

从制导轨迹图14可以看出，本文所设计的导引律成功导引导弹实现了多攻击角度约束条件下的目标全方位立体打击，攻击角度覆盖范围广，角度变化范围大。从图15中的加速度曲线可以看出在大范围攻击角度约束条件下，导弹加速度最大值仍然处于较为合理的区间，小于3g。从图16可以看出在大范围攻击角度约束条件下的初始攻击角度误差变化较大，但在末端时刻均收敛至零，即实现了攻击角度精确控制。从图17可以看出在所有条件下导弹的前置角曲线始终满足视场角约束，小于60°，且在末端时刻均收敛至零。由此可见，本文所提出的算法具有视场角受限情况下的大范围攻击角度控制能力。

表1 攻击角度设置Table 1 Impact angle settings

图14 不同攻击角约束下制导轨迹Fig.14 Guided trajectories with different impact angles

图15 不同攻击角约束下加速度曲线Fig.15 Curves of acceleration with different impact angles

图16 不同攻击角约束下攻击角度误差Fig.16 Impact angle error with different impact angles

图17 不同攻击角约束下前置角曲线Fig.17 Curves of leading angle with different impact angles

4 结 论

对于具有视场角约束的三维攻击角度控制问题，本文基于三维矢量模型和四元数理论实现了制导模型的非奇异表达，并实现了三维比例导引的攻击角度预测，进而根据空间几何关系设计了一种比例导引攻击角度控制方法，能够满足视场角约束条件下的三维攻击角度的精确控制。此外，该制导方法生成的轨迹与导弹速度大小变化无关，进而保证了导弹速度变化情况下的制导性能。文中给出的仿真实例说明了该方法的有效性。